Спосіб визначення глибини залягання та геометричних параметрів випромінюючих осередків гірських порід
Номер патенту: 28474
Опубліковано: 16.10.2000
Автори: Саломатін Валерій Миколайович, Безсмертний Андрій Филимонович
Формула / Реферат
Способ определения глубины залегания и геометрических параметров излучающих очагов горных пород, включающий регистрацию параметров поля в точках на земной поверхности, построение профильных графиков распределения поля над излучающими очагами горных пород, выделение аномалий определение абсцисс экстремальных точек аномальной кривой и определение геометрических параметров излучающих очагов по соотношению экстремальных точек аномальных кривых горизонтальных и вертикальных составляющих поля и параметров излучающих очагов, отличающийся тем что регистрируют параметры естественного импульсного электромагнитного поля Земли, а геометрические параметры излучающих очагов напряженных участков горных пород определяют по абсциссам экстремальных точек выделенных аномалий естественного импульсного электромагнитного поля земли по формулам:
для шара:
по вертикальной составляющей:
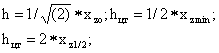
по горизонтальной составляющей:
![]()
для горизонтального кругового цилиндра:
по вертикальной составляющей:
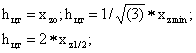
по горизонтальной составляющей:
![]()
для горизонтальной пластины:
по вертикальной составляющей:
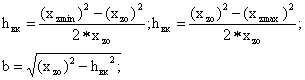
по горизонтальной составляющей:
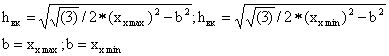
для вертикального пласта не ограниченного по глубине:
по вертикальной составляющей:
![]()
по горизонтальной составляющей:
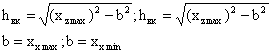
где hцт - глубина до центра тяжести излучающего очага; hвк - глубина до верхней кромки излучающего очага; b – горизонтальная мощность излучающего очага; xzmax - абсцисса точки максимального значения вертикальной составляющей естественного импульсного электромагнитного поля земли Еz; xzo - абсцисса точки перехода через горизонтальную ось графиком вертикальной составляющей естественного импульсного электромагнитного поля земли Еz; xz1/2 - абсцисса точки, в которой значение поля в два раза меньше максимального; xz1/4 - абсцисса точки, в которой значение поля в четыре раза меньше максимального; xzmin - абсцисса точки минимального значения вертикальной составляющей естественного импульсного электромагнитного поля земли Еz; хxo - абсцисса точки перехода через горизонтальную ось графиком горизонтальной составляющей естественного импульсного электромагнитного поля земли Ех; хxmax - абсцисса точки максимального значения поля горизонтальной составляющей естественного импульсного электромагнитного поля земли Еx; xxmin - абсцисса точки минимального значения поля горизонтальной составляющей естественного импульсного электромагнитного поля земли Ex.
Текст
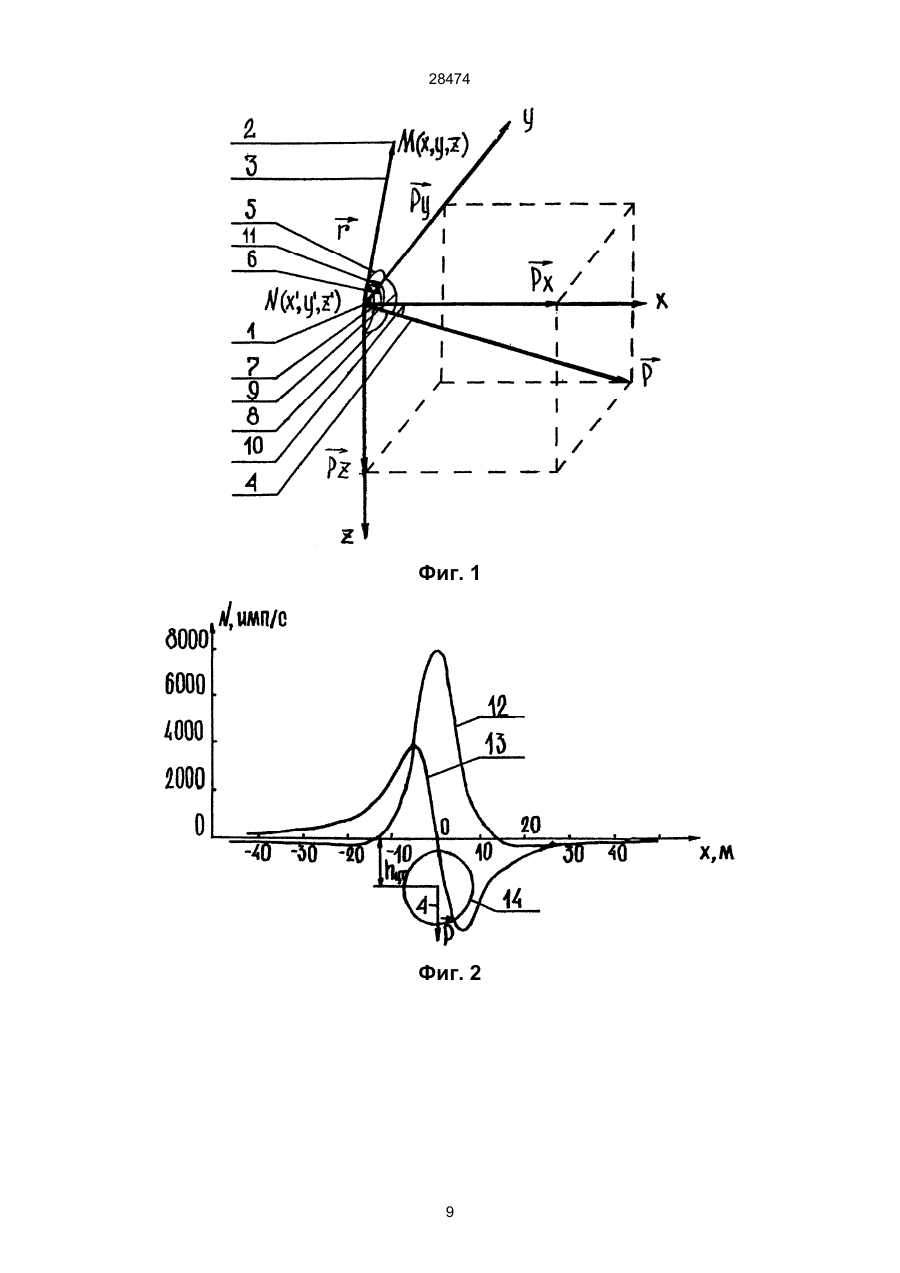
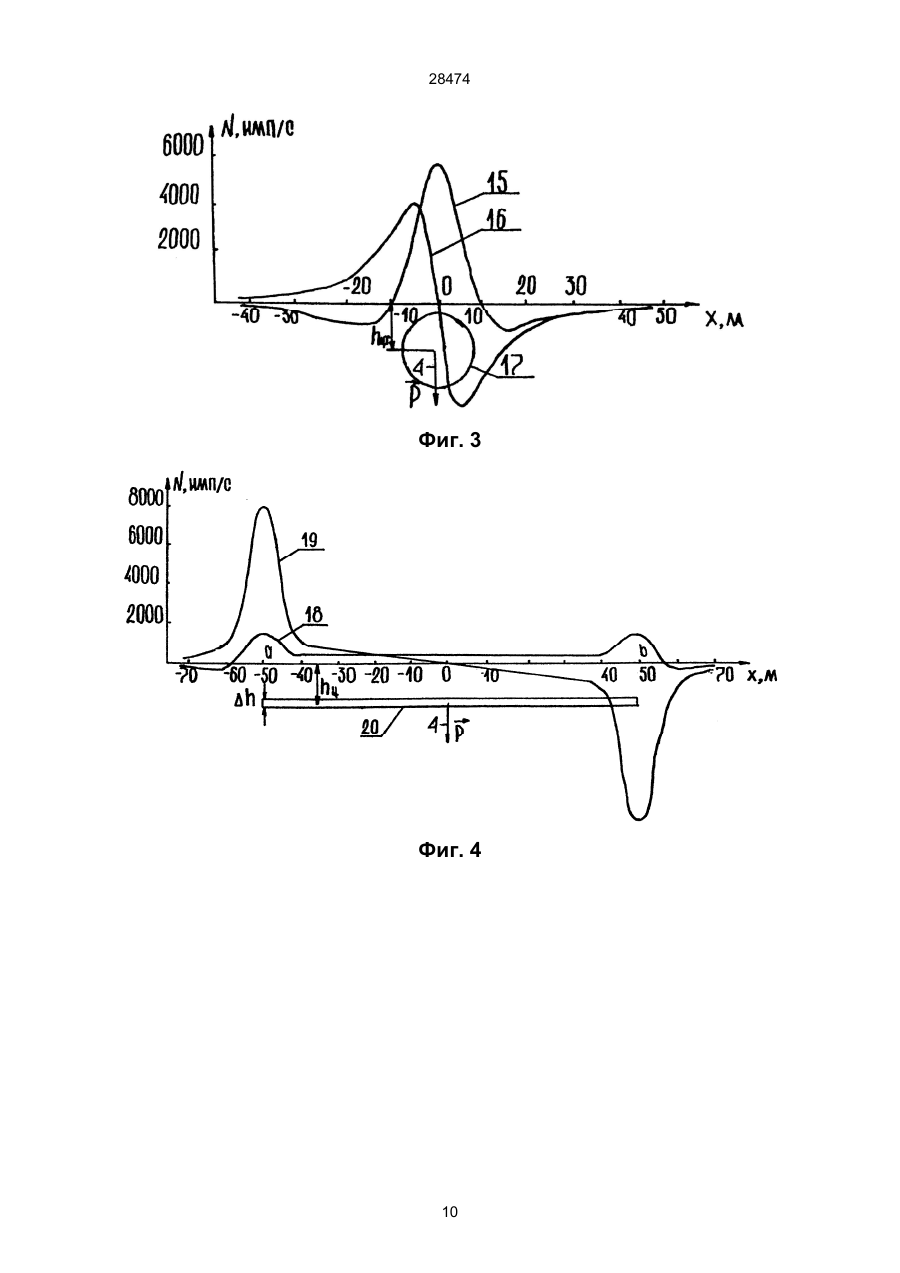
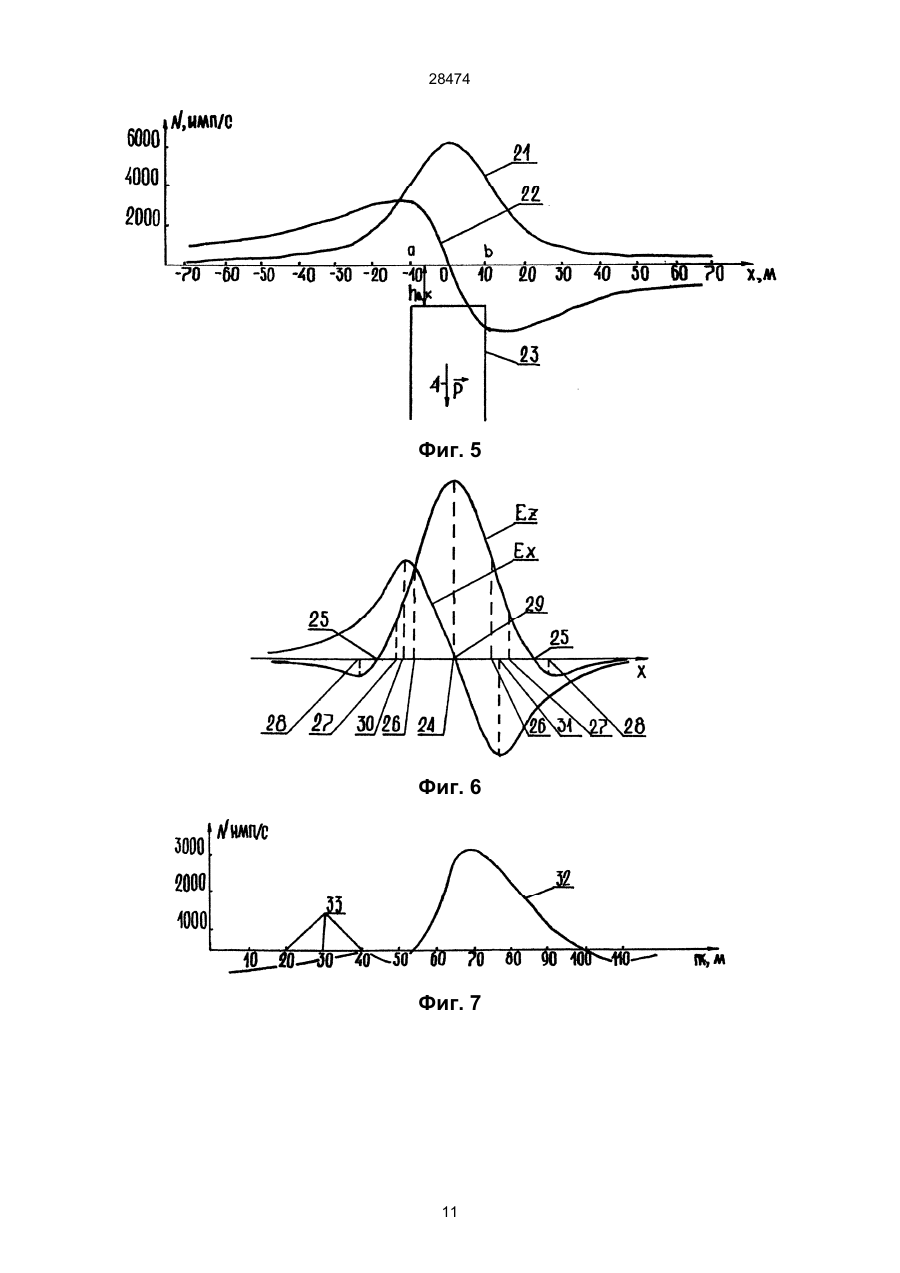
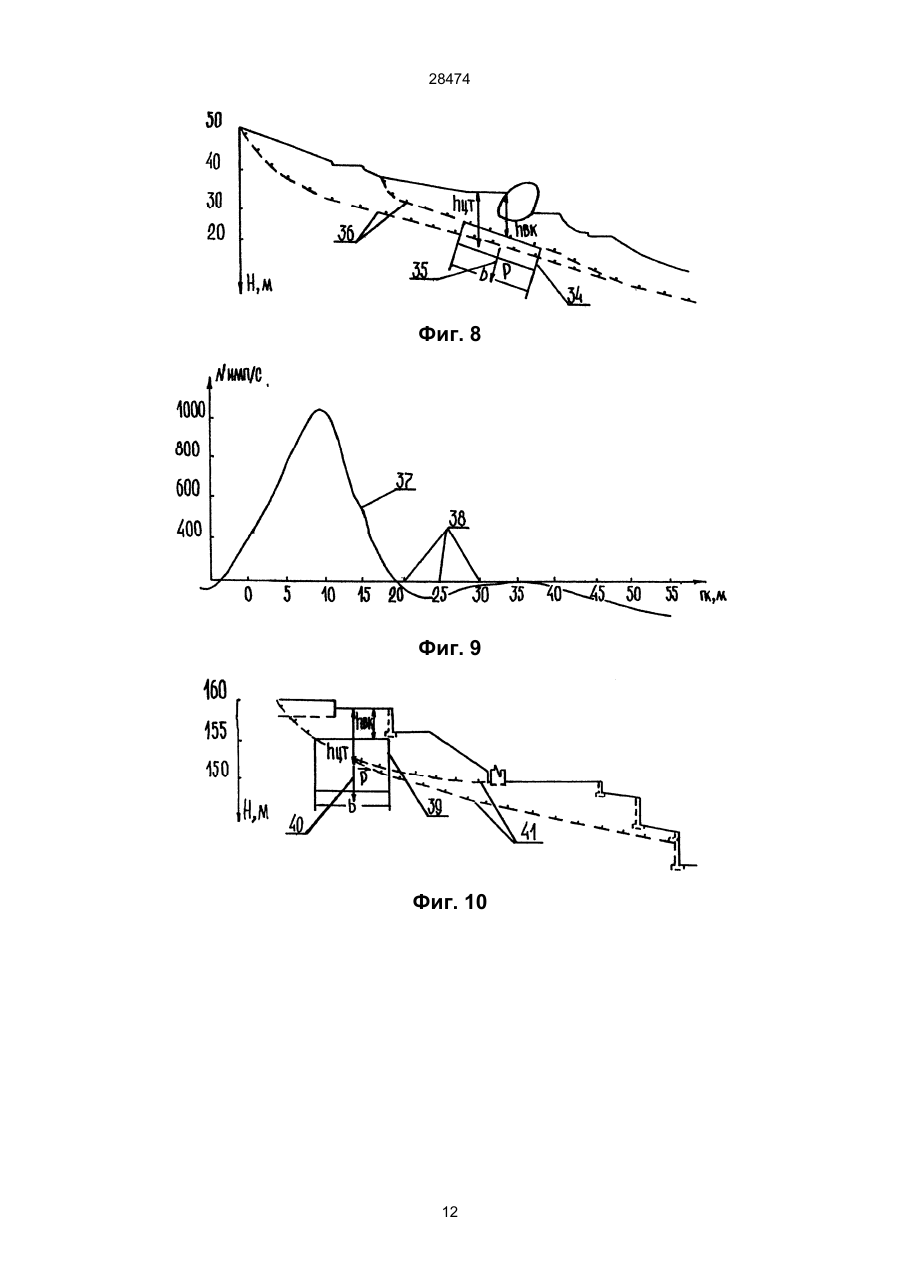
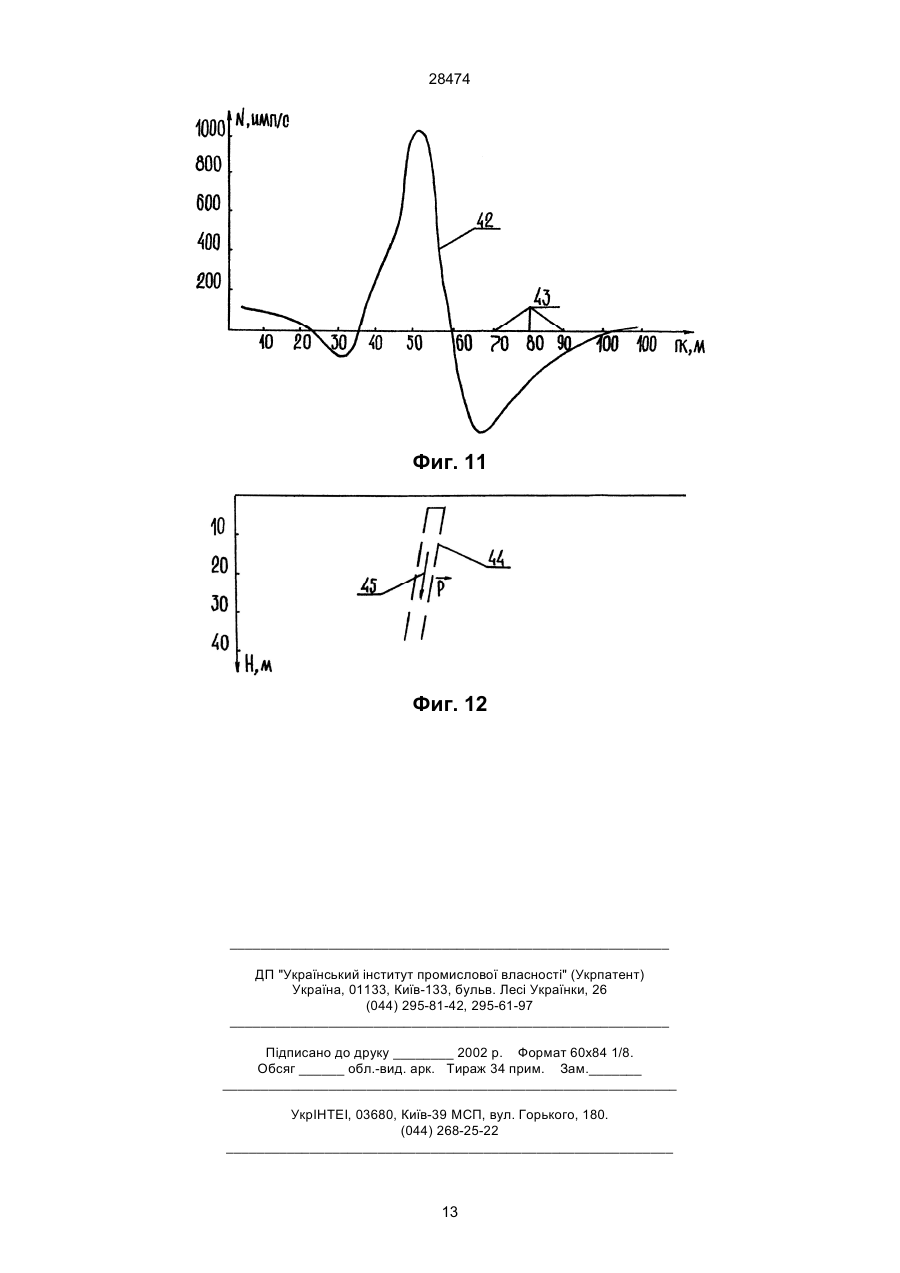
УКРАЇНА (19) UA (11) 28474 (51) МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ A 6 G01V3/08, 3/12 ОПИС ДЕРЖАВНИЙ ДЕПАРТАМЕНТ ІНТЕЛЕКТУАЛЬНОЇ ВЛАСНОСТІ (13) ДО ДЕКЛАРАЦІЙНОГО ПАТЕНТУ НА ВИНАХІД видається під відповідальність власника патенту (54) СПОСІБ ВИЗНАЧЕННЯ ГЛИБИНИ ЗАЛЯГАННЯ ТА ГЕОМЕТРИЧНИХ ПАРАМЕТРІВ ВИПРОМІНЮЮЧИХ ОСЕРЕДКІВ ГІРСЬКИХ ПОРІД hцт = X zo ; hцт = 1/ (3) * X z min ; h цт = 2 * X z1/ 2 ; по горизонтальной составляющей: hцт = (3 ) * X x min ; hцт = - (3) * X x max . для горизонтальной пластины: по вертикальной составляющей: (X z min )2 - (X zo )2 ; hвк = (X zo )2 - (X z max )2 ; 2 * X zo 2 * X zo b = ( X zo )2 - h вк 2 ; по горизонтальной составляющей: hвк = ( (3 ) / 2 * (X x max )2 - b 2 ) ; hвк = ( (3 ) / 2 * (X x min )2 - b 2 ) b = X x max ; b = X x min для вертикального пласта не ограниченного по глубине: по вертикальной составляющей: (X z1/ 4 )2 - (X z1/ 2 )2 ; hвк = (X z max )2 - b 2 ; (X z max )2 - b 2 hвк = b = X x max ; b = X x min где hцт - глубина до центра тяжести излучающего очага; hвк - глубина до верхней кромки излучающего очага; b - горизонтальная мощность излучающего очага; Хzmax - абсцисса точки максимального значения вертикальной составляющей естественного импульсного электромагнитного поля земли Еz; Xz0 - абсцисса точки перехода через горизонтальную ось графиком вертикальной составляющей естественного импульсного электромагнитного поля земли Ez; Xz1/2 - абсцисса точки, в которой значение поля в два раза меньше максимального; Хz1/4 - абсцисса точки, в которой значение поля в четыре раза меньше максимального; Xzmin - абсцисса точки минимального значения вертикальной составляющей естественного импульсного электромагнитного поля земли Ez; Xx0 - абсцисса точки перехода через горизонтальную ось графиком горизонтальной составляющей естественного импульсного электромагнитного поля земли Еx; Ххmax - абсцисса точки максимального зна (13) по горизонтальной составляющей: A (X z1/ 2 )2 - hвк 2 28474 b= 2 * X z1 / 2 (11) hвк = UA hцт = 1/ (2 ) * X zo ; hцт = 1/ 2 * X z min ; hцт = 2 * X z1 / 2 ; по горизонтальной составляющей: hцт = 2 * X x max ; hцт = 2 * X x min . для горизонтального кругового цилиндра: по вертикальной составляющей: hвк = (19) (21) 97041750 (22) 15.04.1997 (24) 16.10.2000 (33) UA (46) 16.10.2000, Бюл. № 5, 2000 р. (72) Саломатін Валерій Миколайович, Безсмертний Андрій Филимонович (73) Саломатін Валерій Миколайович, Безсмертний Андрій Филимонович (57) Способ определения глубины залегания и геометрических параметров излучающих очагов горных пород, включающий регистрацию параметров поля в точках на земной поверхности, построение профильных графиков распределения поля над излучающими очагами горных пород, выделение аномалий, определение абсцисс экстремальных точек аномальной кривой и определение геометрических параметров излучающих очагов по соотношению экстремальных точек аномальных кривых горизонтальных и вертикальных составляющих поля и параметров излучающих очагов, отличающийся тем, что регистрируют параметры естественного импульсного электромагнитного поля Земли, а геометрические параметры излучающих очагов напряженных участков горных пород определяют по абсциссам экстремальных точек выделенных аномалий естественного импульсного электромагнитного поля земли по формулам: для шара: по вертикальной составляющей: 28474 чения поля горизонтальной составляющей естественного импульсного электромагнитного поля земли Ех; Хxmin - абсцисса точки минимального зна чения поля горизонтальной составляющей естественного импульсного электромагнитного поля земли Еx. Изобретение относится к геофизике, а именно к способам инженерной геологии, основанным на измерении естественного импульсного электромагнитного поля Земли (ЕИЭМПЗ). Известен, принятый за прототип, способ определения глубины залегания возмущающих объектов по соотношениям характерных точек магнитных полей и элементов залегания (глубина центра тяжести и верхней кромки, горизонтальная мощность, угол падения и т. д.) геологических тел ("Магниторазведка", Справочник геофизика. - М.: Недра, 1990. - 470 стр., страница 309). Способ заключается в изучении распределения магнитного поля (вертикальной или горизонтальной составляющей) на земной поверхности по сетке профилей. После построения профильных графиков магнитного поля выделяются аномалии, связанные с наличием в земной коре скоплений магнитосодержащих минералов. В дальнейшем, при количественной интерпретации полевого материала определяют абсциссы характерных точек магнитных аномалий, используя которые, решают обратную, задачу и определяют различные параметры геологических тел, - глубину заложения центра тяжести для тел с центральной симметрией, глубину до верхней кромки и горизонтальную мощность для крутопадающих тел и горизонтальных пластов. Признаками прототипа, совпадающими с существенными признаками предполагаемого изобретения являются регистрация параметров поля в точках на земной поверхности, построение профильных графиков распределения поля над излучающими очагами, выделение аномалий, определение абсцисс экстремальных точек аномальной кривой, определение геометрических параметров излучающих очагов по соотношении) экстремальных точек аномальных кривых и параметров излучающих очагов. Причинами препятствующими достижению технического результата: определение глубины залегания и геометрических параметров очагов напряженно-деформированного состояния горных пород в прототипе являются: в прототипе необходимо проявление магнитной аномалии от геологических объектов, включающих магнитосодержащие минералы, чего недостаточно для определения очагов напряженно-деформированного состояния горных пород. В основу изобретения поставлена задача получения способа определения глубины залегания и геометрических параметров излучающих очагов горных пород путем определения абсцисс экстремальных точек аномальной кривой ЕИЭМПЗ по профилям полученным вкрест простирания аномальных объектов и решения обратной задачи (определение параметров тела создающего ЕИЭМПЗ измеренного на поверхности Земли) с помощью формул и за счет этого обеспечивается технический результат и получают следующие потребительские свойства: определяют глубину и ге ометрические параметры зон массового трещинообразования, фильтрационных потоков и появления деформаций, а также определяют модель первого приближения геологического тела, с которым связаны очаги напряженно-деформированного состояния горных пород. В способе определения глубины залегания излучающих очагов горных пород, включающем регистрацию параметров поля в точках на земной поверхности, получение профильных графиков распределения поля над излучающими очагами горных пород, выделение аномалий, определение абсцисс экстремальных точек аномальной кривой и определение геометрических параметров очагов по соотношению экстремальных точек и параметров излучающих очагов; изучается распределение ЕИЭМПЗ, которое создается источниками, располагающимися непосредственно в литосфере и доступно наблюдению на удалении от них. Источниками ЕИЭМГТЗ являются массивы горных пород, в которых под действием механических напряжений разнообразного происхождения, включая и гидродинамический фактор, происходят необратимые деформации зерен минералов-диэлектриков или капиляров, заполненных электролитом, нарушения двойных электрических слоев. Поскольку в природных диэлектриках избыточный электрический заряд одного знака индуцирует возникновение заряда другого знака, избыточный дипольный момент возникает всегда и состояние поляризации является общим свойством источника ЕИЭМПЗ. На основании этого, для обеспечения решения поставленной задачи необходимо получить формулы связи между экстремальными точками аномалии ЕИЭМПЗ и геометрическими параметрами очагов напряженно-деформированного состояния горных пород (излучающих очагов). Учитывая природу возникновения ЕИЭМПЗ над возмущающими объектами предположим, что любое аномальное тело, в какой-то, достаточно короткий, момент времени dt можно рассматривать как систему бесконечно большого числа элементарных электрических диполей с упорядочение расположенными осями дипольных моментов. Потенциал элементарного электрического диполя выражается формулой: Ù dP dUэд = * cos(p r ) (1) r2 где: dP - электрический момент диполя в случае естественной поляризации: (2) dp = p * dV p - вектор плотности тока в очаге поляризации; r - радиус-вектор между центром элементарного электрического диполя и точкой наблюдения; ® r = 2 (x - x')2 + (y - y')2 + (z - z')2 (3) 28474 Следовательно: æ Ù ö ç p r ÷ - угол между вектором плотности тока диç ÷ è ø ( ) æ Ù ö æ Ù ö cos P Ùr = cosç p x ÷ * cosç r x ÷ + è ø è ø æ Ù ö æ Ù ö + cosç p y ÷ * cosç r y ÷ + (5) è ø è ø æ Ù ö æ Ù ö + cosç p z ÷ * cosç r z ÷ , è ø è ø а проекции вектора плотности тока на координатные оси: æ Ù ö æ Ù ö p x = p * cosç p x ÷ ; p y = p * cosç p y ÷ ; è ø è ø (6) Ù ö æ p z = p * cosç p z ÷ . è ø Тогда, потенциал поляризованного тела в однородном пространстве запишем в виде: æ Ù ö æ Ù ö cosç r x ÷ cosç r y ÷ è ø dV + è ø dV + p * Uпт = p x * ò y ò 2 2 V V r r (7) æ Ù ö cosç r x ÷ è ødV. + pz * ò 2 V r Продифференцируем это выражение. Дифференцирование выполним по координатам точки наблюдения (х, у, z) (см. фиг. 1), а интегрирование - по координатам тела (x', y', z'), поэтому дифференцирование может быть выполнено под знаком интеграла. Получим три составляющие напряженности поля (Ех, Еу - горизонтальные, Еz - вертикальная): поля и радиусом-вектором; dV - элементарный объем, занимаемый элементарным электрическим диполем. Суммируя действие элементарных диполей в интересующем нас объеме получим потенциал поляризованного тела в однородном пространстве, которое излучает ЕИЭМПЗ: æ Ù ö cosç p r ÷ (4) è ø dV . Uпт = P * ò 2 V r От потенциальной функции с помощью общеизвестных формул переходим к выражениям напряженности поля. Способ иллюстрируется следующими чертежами: на фиг. 1 - изображен в декартовой системе координат вектор плотности тока поляризованного тела p в однородном пространстве; на фиг. 2-5 изображены вычисленные графики распределения вертикальной и горизонтальной составляющей ЕИЭМПЗ от заранее выбранных первичных геометрических моделей излучающих очагов; на фиг. 6 - изображены экстремальные точки аномальных графиков; на фиг. 7, 9, 11 - изображены аномальные кривые вертикальной составляющей ЕИЭМПЗ; на фиг. 8, 10, 12 - изображены очаги напряженно-деформированного состояния горных пород на инженерно-геологических разрезах; на фигуре 1 обозначены: поз 1 - центр элементарного электрического диполя; поз 2 - точка наблюдения; поз 3 - радиус-вектор между центром элементарного электрического излучающего диполя 1 и Ex = px * ò 2(x - x ')2 - (y - y ')2 - (z - z')2 V точкой наблюдения 2; поз 4 - p - вектор плотности тока элементарного электрического излучающего диполя; поз 5 - угол между радиусом-вектором 3 и æ Ù ö осью Оу - ç r y ÷ ; поз 6 - угол между радиусомè ø * ò (x - x') * (y - y') dV + + 3p z * ò r (x - x') * (z - z' ) r V Ey = py * æ Ù ö радиусом-вектором 3 и осью Оz - ç r z ÷ ; поз 8 è ø угол между направлением вектора плотности тоæ Ù ö ка 4 æ p ö и осью Oz - ç p z ÷ ; поз 9 - угол между наç ÷ è ø è ø ò 5 ò (y - y') * (x - x') dV + + 3p z * ò r (y - y') * (z - z' ) r V E z = pz * ò 5 * ò (z - z' ) * (x - x') dV + dV + 3p x * (8) + 3p y * dV r 5 5 V ò V 3 5 2(z - z')2 - (x - x ')2 - (y - y' )2 V æ Ù ö вектора плотности тока 4 æ p ö и осью Ох - ç p x ÷ ; ç ÷ è ø è ø поз 11 - угол между направлением вектора плотæ Ù ö ности тока 4 æ p ö и радиусом-вектором 3 - ç p r ÷ . ç ÷ è ø è ø r 5 V æ ö правлением вектора плотности тока 4 ç p ÷ и осью è ø æ Ù ö Оу - ç p y ÷ ; поз 10 - угол между направлением è ø dV + 3p y * dV 2(y - y ')2 - (x - x ')2 - (z - z')2 V * 5 5 V æ Ù ö вектором 3 и осью Ох - ç r x ÷ ; поз 7 - угод между è ø r r (z - z') * (y - y') r 5 dV dV + 3p x * 28474 Рассмотрим случай, когда тело можно считать бесконечно вытянутым вдоль одной из горизонтальных осей координат. Опуская промежуточные вычисления получим: (z - z' )2 - (x - x')2 dS + ò 2 S ((x - x')2 + (z - z' )2 ) (x - x') - (z - z') dS ; + 4p z * ò 2 2 2 S ((x - x') + (z - z') ) (x - x') - (z - z') dS + E z = 4p x * ò 2 S ((x - x ')2 + (z - z' )2 ) (z - z')2 - (x - x')2 dS. + 2p z * ò 2 2 2 S ((x - x' ) + (z - z') ) ò E zoz = E z = p * 2(h - h')2 - (x - x' )2 - (y - y' )2 dV . 5 r После интегрирования и учитывая, что дипольный момент естественно поляризованного тела V E x = -2p x * равен P = p * V окончательно получим: (x - x') * (h - h') ; E x = 3P * 5 r (y - y') * (h - h') ; E y = 3P * (11) 5 r 2(h - h')2 - (x - x ')2 - (y - y ')2 Ez = P * . 5 r Горизонтальный круговой цилиндр 17 (фиг. 3) можно отнести телам бесконечно вытянутым относительно горизонтальной оси координат (примем вдоль оси Оу). Поэтому обратимся к формулам двухмерных тел (9). Аналогично шару 14 (фиг. 2) рассмотрим вертикально однородно поляризованный цилиндр 17: (x - x') * (h - h') dS ; E zox = E x = 4p * ò 4 S r (12) (h - h')2 - (x - x')2 dS . E zoz = E z = 2p * ò 4 S r Решая плоскую задачу можно рассматривать координаты (x', h') как координаты фиксированной точки (центра поперечного сечения цилиндра). Поэтому функция может быть вынесена за знак интеграла. В результате преобразований получим выражения функции для горизонтального кругового цилиндра 17: (x - x') * (h - h') ; E x = 4P * 2 (x - x')2 + (h - h')2 (13) (h - h')2 - (x - x')2 E z = 2P * 2 (x - x')2 + (h - h')2 На фиг. 4, показана горизонтальная пластина 20. Представим ее ограниченной по оси Ох координатами а и b и по глубине h1 и h2, глубину до центральной горизонтальной оси тела обозначим через h. Воспользуемся формулами (9): (9) На фиг. 2 - поз. 12 - вертикальная составляющая, поз. 13 - горизонтальная составляющая ЕИЭМПЗ от геометрической модели шара поз. 14. На фиг. 3 - поз. 15 - вертикальная составляющая, поз. 16 - горизонтальная составляющая ЕИЭМПЗ от геометрической модели горизонтального кругового цилиндра - поз. 17. На фиг. 4 - поз. 18 - вертикальная составляющая, поз. 19 - горизонтальная составляющая ЕИЭМПЗ от геометрической модели горизонтальной пластины - поз. 20. На фиг. 5 - поз. 21 - вертикальная составляющая, поз. 22 - горизонтальная составляющая ЕИЭМПЗ от геометрической модели вертикального пласта, не ограниченного по глубине - поз. 23. По осям Ох отложен шаг наблюдений в метрах, по осям Оу - скорость счета ЕИЭМПЗ в импульсах в секунду. Буквами обозначены: p - вектор поляризации 4; на фиг. 2, 3 hцт - глубина центра тяжести модели; на фиг. 4 hцт - глубина центральной горизонтальной оси модели; на фиг. 5 hвк - глубина верхней кромки очага; Dh - мощность модели горизонтальной пластины; а и b - левая и правая границы моделей. Этих моделей достаточно для аппроксимации реальных очагов напряженно-деформированного состояния горных пород. Решая для этих моделей прямую задачу, рассчитаем распределение ЕИЭМПЗ на поверхности, создаваемое ими. Для облегчения восприятия информации и снижения объема записей примем начальное условие: будем считать, что объекты поляризованы вертикально вниз. Рассмотрим вертикально и однородно поляризованный шар 14 (фиг. 2). В данном случае он может быть отождествлен либо с полюсом находящимся в его центре, либо с элементарным диполем с совпадающим центром. В связи с тем, что вектор поляризации 4 параллелен оси Оz для получения выражений Ех, Еy, Ez используем из (8) ( ) ( ) (x - x' ) * (h - h' ) dx' dh' ; 2 a h ((x - x')2 + (h - h')2 ) bh (h - h')2 - (x - x')2 dx' dh' . E z = 2p * ò ò 2 a h ((x - x' )2 + (h - h')2 ) b h2 E x = 4P * ò ò 1 (14) 2 1 После интегрирования представленных интегралов получим выражение для составляющих ЕИЭМПЗ от горизонтальной пластины 20. С учетом, что дипольный момент сечения пластины 20 вертикальной плоскостью можно представить как: (15) P = p * (h2 - h1 ) * (b - a) получим: проекции Еzох, Ezоy, Ezоz соответственно, а p =pz: (x - x') * (h - h') dV ; E zox = E x = 3p * ò 5 V r (10) (y - y') * (h - h') dV ; E zoy = E y = 3p * ò 5 V r E x = -2P * E z = 2P * 4 ((x - b) 2 (h - h') * (2x - b - a ) )( + (h - h')2 * (x - a)2 + (h - h')2 ) (h - h') - (x - b ) * (x - a) ((x - b)2 + (h - h')2 )* ((x - a)2 + (h - h')2 ). 2 (16) 28474 точки перехода через горизонтальную ось графиком вертикальной составляющей ЕИЭМПЗ Ez; поз. 26 - Хz1/2: абсцисса точки в которой значение поля в два раза меньше максимального; поз. 27 Хz1/4: абсцисса точки в которой значение поля в четыре раза меньше максимального; поз. 28 Хzmin: абсцисса точки минимальных значений вертикальной составляющей ЕИЭМПЗ Еz: поз. 29 Хxо: абсцисса точки перехода через горизонтальную ось графиком горизонтальной составляющей ЕИЭМПЗ Еx; поз. 30 - Хxmax: абсцисса точки максимального значения поля горизонтальной составляющей ЕИЭМПЗ Еx; поз. 31 - Xxmin: абсцисса точки минимального значения поля горизонтальной составляющей ЕИЭМПЗ Ex. Установим их связь с элементами залегания возмущающих объектов. Шар 14 (фиг. 2). Используем выражение (19). Исследуем функцию Еz. Определим точки перехода функции через ноль из условия, Рассмотрим вертикальный пласт бесконечной мощности 23 (фиг. 5), с глубиной верхней кромки hвк, ограниченный по оси Ох от а до b. Модель относится к двухмерным телам, поэтому используем формулы (9), а с учетом вертикальной поляризации используем составляющие Ezоx, Ezоz: (x - x') * (h - h') dx' dh' ; 2 a h ((x - x' )2 + (h - h')2 ) bh (h - h')2 - (x - x')2 dx' dh' . E z = 2p * ò ò 2 a h ((x - x' )2 + (h - h')2 ) b h2 E x = 4p * ò ò 1 (17) 2 1 После интегрирования получим: E x = -p * ln (h - h')2 + (x - b)2 ; (h - h' )2 + (x - a)2 (18) x -b x-aö æ E z = 2p * ç arctg - arctg ÷. h - h' h - h' ø è Таким образом, используя полученные выражения для составляющих напряженности ЕИЭМПЗ решим обратную задачу для определения глубины залегания и геометрических параметров очагов напряженно-деформированного состояния горных пород, в том числе и связанных с фильтрационными потоками подземных вод. Для облегчения дальнейших преобразований, модели рассматривались в системе координат с началом расположенным над центром тяжести используемых очагов. Поэтому вычислительные формулы примут вид (см. фиг. 2-5): для шара 14: -hцт * x E x = 3P * ; 5/2 2 hцт + x 2 (19) 2hцт 2 - x 2 Ez = P * 5/2 hцт 2 + x 2 для горизонтального кругового цилиндра 17: -hцт * x E x = 4P * ; 2 2 x 2 + hцт (20) hцт 2 - x 2 E z = 2P * 2 x 2 + hцт 2 для горизонтальной пластины 20: -hвк * x E x = -4P * ; 2 (x - b) + hвк 2 * (x + b)2 + hвк 2 (21) 2 hвк + b 2 - x 2 E z = 4P * . (x - b)2 + hвк 2 * (x + b )2 + hвк 2 для вертикального пласта не ограниченного по глубине 23: ( (23) X zo = hцт * (2) . Найдем критические точки функции Еz из условия, что производная функции в этих точках равна нулю. При преобразовании получим, что таких точек на графике три. Одна из них принимает нулевое значение. В этой точке аномалия Ez принимает максимальное значение 24 (фиг. 6): Xzmax=0. (24) Два других значения Хz характеризует положение минимумов аномальной кривой 28 (фиг. 6): Xzmin=2hцт. (25) Рассмотрим точки, в которых поле: Ez=1/2*Ezmax. Подставим в формулу (19): X=1/2*hцт, получим, что: ) ( ) ( E z = P / hцт 3 , а E z max = 2 * P / hцт 3 , Таким образом 26 (виг. 6): Xz1/2=1/2*hцт (26) Исследуем функцию горизонтальной составляющей Ех ЕИЭМПЗ. Из формулы (19) видно, что Ех равна нулю в начале координат, то есть в точке Хxо. Определим критические точки функции Ех из условия, что производная функции в этих точках равна нулю. В результате получим 30, 31 (фиг. 6): X x min = hцт / 2; X x max = -hцт / 2. (27) Горизонтальный круговой цилиндр 17 (фиг. 3). Рассмотрим функции определенные от горизонтального кругового цилиндра 17 из (20). Определим точки перехода через ноль для функции Еz 25 (фиг. 6): Xzo=hцт. (28) Критические точки определим из условия, что (Еz)'=0,28 (фиг. 6): ) ( ) )( ( ( E x = -p * ln 2hцт 2 - x 2 = 0 следовательно 25 (фиг. 6): ) )( ) hвк + (x - b) 2 2 hвк 2 + (x + b)2 ; (22) æ x -b x+bö - arctg ÷. E z = 2p * ç arctg ç h вк hвк ÷ ø è Для этого из проанализируем приведенные выше функции (19-22) определим экстремальные точки аномальных графиков (фиг. 6). На фиг. 6 изображены экстремальные точки аномальных графиков: поз. 24 - Хzmax: абсцисса точки максимального значения вертикальной составляющей ЕИЭМПЗ Еz; поз. 25 - Хzo: абсцисса (29) Xzmax=0 Xzmin=hцт* (3) . Определим точки, в которых функция принимает половинное значение. Для этого сравним функции Ez/2 и Ezmax: E z max = 2P * 1 / hцц2 ; E z = P * 1 / hцц2 следовательно 26 (фиг. 6): 5 28474 Анализируя функцию горизонтальной составляющей ЕИЭМПЗ получим следующие формулы 30, 31 (фиг. 6): X z1/ 2 = 1/ 2 * hцт . (30) Рассмотрим горизонтальную составляющую ЕИЭМПЗ Ех и определим ее критические точки. Из формулы (20) видно, что функция Ex в начальной точке координат принимает нулевое значение. Из условия (Ех)'=0 определим критические точки кривой 30, 31 (фиг. 6): ( (31) X x min = hцт / (3 ) ; X х max = -hцт / (3). Горизонтальная пластина 20 (фиг. 4). Горизонтальная пластина представляет собой горизонтальный пласт ограниченный по прямой Ох координатами -b и b, мощность которой намного меньше чем глубина залегания ее верхней кромки. Пластина расположена на глубине hBK. Определим точки, в которых функция Еz переходит через ноль. После преобразований получим 25 (фиг. 6): ( ) (32) X zo = hвк 2 + b 2 . Из анализа на критические точки можно сделать следующие выводы: 1) в начале координат функция не принимает максимального значения; 2) функция имеет два максимума расположенных в точках 24 (фиг. 6): X z max = (X zo )2 - 2(X zo ) * hвк ; 3) минимальные значения функция принимает в точках с абсциссами 28 (фиг. 6): (34) X z min = (X zo )2 + 2(X zo ) * hвк . Для горизонтальной составляющей Еx в начальной точке системы координат принимает нулевое значение, а максимальные и минимальные значения принимает в точках с абсциссами 30, 31 (фиг. 6): ( ) ( 2 ) hцт = X zo ; hцт = 1/ (3) * X z min ; h цт = 2 * X z1/ 2 ; по горизонтальной составляющей: hцт = (3 ) * X x min ; hцт = - (3) * X x max . для горизонтальной пластины: по вертикальной составляющей: (35) (38) (39) hвк (40) (41) (X z min )2 - (X zo )2 ; hвк = Вертикальный пласт бесконечной мощности 23 (фиг. 5). Считаем, что вертикальный пласт ограничен по оси Ох координатами -b и b, глубина до верхней кромки - hвк. Рассмотрим функцию (22). Анализ функции Еz показывает, что аномалия имеет одну критическую точку, которая соответствует положению максимума графика 24 (фиг. 6): Xzmax=0. Также отметим, что переход через ноль у этой функции не возможен. Поэтому для получения формул решения обратной задачи обратимся к точкам в которых: Ez=1/2*Ezmax; и Ez=1/4*Ezmax. Получим систему исходных выражений: X z1/ 2 - b X b +b ì ; - arctg z1/ 2 = arctg ïarctg hвк hвк hвк ï í ï2 * æ arctg X z1/ 4 - b - arctg X z1/ 4 + b ö = arctg b . ç ÷ ÷ ï ç hвк hвк h вк ø î è 26, ) для горизонтального кругового цилиндра: по вертикальной составляющей: X x min = 2 / (3) * b 2 + hвк . После преобразований получим (фиг. 6): ì 2 2 ïb = (X z1/ 2 ) - hвк ; í ï X z1/ 4 = (X z1 / 2 )2 + 2hвк * (X z1/ 2 ). î ( hцт = 1/ (2 ) * X zo ; hцт = 1/ 2 * X z min ; hцт = 2 * X z1 / 2 ; по горизонтальной составляющей: hцт = 2 * X x max ; hцт = 2 * X x min . (33) X x max = - 2 / (3) * b 2 + hвк 2 ; ) (37) X x max = hвк 2 + b 2 ; X x min = - h вк 2 + b 2 . Поставленная задача решается тем, что в способе определения глубины залегания и геометрических параметров излучающих очагов горных пород, включающем регистрацию параметров поля в точках на земной поверхности, построения профильных графиков распределения поля над излучающими очагами горных пород, выделение аномалий, определение абсцисс экстремальных точек аномальной кривой и определение геометрических параметров излучающих очагов по соотношению экстремальных точек аномальных кривых и параметров излучающих очагов, согласно изобретению регистрируют параметры ЕИЭМПЗ и связи между экстремальными точками аномалии ЕИЭМПЗ и геометрическими параметрами излучающих очагов напряженно-деформированного состояния горных пород определяют по абсциссам экстремальных точек выделенных аномалий ЕИЭМПЗ по формулам. Для шара: по вертикальной составляющей: 2 * X zo (X )2 - (X z max )2 ; = zo (42) 2 * X zo 2b = 2 * (X zo )2 - hвк 2 ; по горизонтальной составляющей: (3) / 2 * ((X x max )2 - b 2 ) ; hвк = (3) / 2 * ((X x min )2 - b 2 ) hвк = (43) b = X x max ; b = X x max для вертикального пласта не ограниченного по глубине: по вертикальной составляющей: hвк = (X z1 / 4 )2 - (X z1/ 2 )2 ; 2 * X z1/ 2 b= 27 (X z1 / 2 ) 2 - hвк (44) 2 по горизонтальной составляющей: (X z max )2 - b2 ; = - (X z max )2 - b 2 hвк = (36) hвк b = X x max ; b = X x min 6 (45) 28474 денные формулы получим глубину центра тяжести: для шара 14 (фиг. 2): hцт=2,1 см; для горизонтального кругового цилиндра 17 (фиг. 3): hцт 1,6 см; для горизонтальной пластины 20 (фиг. 4) небольшой горизонтальной мощности найдем глубину до верхней кромки hвк и горизонтальную мощность b: hвк=0,7 см; b=2,7 см. Аналогично определим вышеуказанные параметры для правой ветви аномальной кривой 26, 25, 28 (фиг. 6): Хz1/2=3,0 см; Хzo=6,1 см; Xzmin=8,6 см. для шара 14 (фиг. 2) hцт=3,9 см; для горизонтального кругового цилиндра 17 (фиг. 3) hцт=3,0 см. Для горизонтальной пластины 20 (фиг. 4) небольшой горизонтальной мощности: hвк=3,0 см; b=5,3 см. Найдем средние значения по обоим ветвям кривой для шара 14 (фиг. 2) hцт =3,0 см; для горизонтального кругового цилиндра 17 (фиг. 3) hцт= =2,3 см; для горизонтальной пластины небольшой горизонтальной мощности 20 (фиг. 4) hвк=1,8 см b=4,0 см. Осредним Hцт для всех методов определения Нцт=2,9 см. Определим среднеквадратичную погрешность определения параметров по формуле: где: hцт - глубина до центра тяжести излучающего очага; hвк глубина до верхней кромки излучающего очага; b - горизонтальная мощность излучающего очага; Хzmax - абсцисса точки максимального значения вертикальной составляющей ЕИЭМПЗ Еz; Xzo - абсцисса точки перехода через горизонтальную ось графиком вертикальной составляющей ЕИЭМПЗ Ez; Xz1/2 - абсцисса точки, в которой значение поля в два раза меньше максимального; Хz1/4 - абсцисса точки, в которой значение поля в четыре раза меньше максимального; Xzmin - абсцисса точки минимальных значений вертикальной составляющей ЕИЭМПЗ Ez; Xxo - абсцисса точки перехода через горизонтальную ось графиком горизонтальной составляющей ЕИЭМПЗ Еx; Ххmax абсцисса точки максимального значения поля горизонтальной составляющей ЕИЭМПЗ Ех; Хxmin абсцисса точки минимального значения поля горизонтальной составляющей ЕИЭМПЗ Еx. Между совокупностью существенных признаков изобретения и достигаемым техническим результатом существует следующая причинно-следственная связь: при наличии совокупности всех достаточных во всех случаях существенных, признаков возможно определение глубины залегания и геометрических параметров очагов напряженнодеформированного состояния горных пород, при отсутствии существенных признаков технический результат не будет достигнут. Изобретение сопровождается практическими примерами определения количественных характеристик изучаемых очагов механических напряжений. На фиг. 7 изображены - поз. 32 - аномальная кривая вертикальной составляющей ЕИЭМПЗ; поз. 33 - пикеты наблюдений на профиле. По оси Оу - дана градация скорости счета ЕИЭМПЗ в импульсах в секунду. Измерения проводились в районе пгт Алупка. По внешнему виду аномалии видно, что ось поляризации аномального объекта расположена наклонно по отношению к вертикальной плоскости. Также, учитывая априорные данные, необходимо аппроксимировать очаг напряжений горизонтальным пластом небольшой горизонтальной мощности (очаг напряжений связан с плоскостями скольжения оползневого тела). Поэтому воспользуемся формулами для определения глубины заложения центра тяжести для шара (38), горизонтального кругового цилиндра (40), а также для вычисления глубины до верхней кромки горизонтальной пластины и ее горизонтальной мощности (42). Расчеты проведем отдельно для обоих ветвей аномальной кривой и затем вычислим средние значения искомых параметров. Определим, для левой ветви графика 26, 25, 28 (фиг. 6): X z1/ 2 = 1,6 см; X zo = 2,8 см; X z min = 3,4 см. Условное начало координат присвоим абсциссе точки с максимальным значением ЕИЭМПЗ 24 (фиг. 6). Использование нескольких формул для определения геометрических параметров очага механических напряжений необходимо для уменьшения случайной погрешности. Используя приве å (hцт - Hцт ) 2 (46) 2*n где: n - количество определений глубины заложения центра тяжести. Точность определения глубины центра тяжести очага напряженно-деформированного состояния горных пород составляет 0,8 см, глубины до верхней кромки объекта 0,8 см, горизонтальной мощности - 0,9 см. Переведем вычисленные параметры очага напряженно-деформированного состояния горных пород из сантиметров в метры: hцт=2,9 см * 5 м=14,2 м; hвк=1,8 см * 5 м=9,3 м; b=4,0 см * 5 м=20,0 м. На фиг. 8 обозначены - поз. 34 - очаг напряженно-деформированного состояния горных пород на осевом инженерно-геологическом разрезе оползня построенном при инженерно-геологических изысканиях, - поз. 35 - вектор плотности тока (равнозначен поз. 4); поз. 36 - плоскости скольжения оползневого тела. На фиг. 8 буквами обозначены hцт - глубина до центра тяжести очага напряженно-деформированного состояния горных пород; hвк - глубина до верхней кромки очага напряженно-деформированного состояния горных поM= n род; p - вектор плотности тока 35, 4; b - горизонтальная мощность очага напряженно-деформированного состояния горных пород. Учитывая, что левая ветвь аномальной кривой круче чем правая, отметим, что вектор плотности тока (поз. 35, 4) в очаге напряженно-деформированного состояния горных пород (поз. 34) наклонен по отношению к вертикали в сторону крутой ветви. То есть целесообразно аномальное тело изобразить наклонным по отношению к горизонту так, что бы очаг механических напряжений был параллелен плоскостям скольжения оползневого тела (поз. 36). 7 28474 В целом, отметим, что центр тяжести очага напряженно-деформированного состояния горных пород соответствует пространственному положению нижней плоскости скольжения, а верхняя кромка, объекта совпадает с положением верхней плоскости скольжения (если учесть наклон очага). На фиг. 9 изображены - поз. 37 - аномальная кривая вертикальной составляющей ЕИЭМПЗ; поз. 38 - пикеты наблюдений на профиле. По оси Оу - дана градация скорости счета ЕИЭМПЗ в импульсах в секунду. Расчет производился с помощью тех же методов, которые приведены выше. Укажем только конечные значения геометрических параметров очага напряженно-деформированного состояния горных пород определенные по аномальной кривой: hцт=6,9 м; hвк=3,5 м; b=10,5 м. Параметры определены с точностью: Мhцт=0,15; Мhвк=0,05; Мh=0,14. На фиг. 10 обозначены - поз. 39 - очаг напряженно-деформированного состояния горных пород на осевом инженерно-геологическом разрезе оползня построенном при инженерно-геологических изысканиях; поз. 40 - вектор плотности тока (равнозначен поз. 4); поз. 41 - плоскости скольжения оползневого тела. На фиг. 10 буквами обозначены hцт - глубина до центра тяжести очага напряженно-деформированного состояния горных пород; hвк - глубина до верхней кромки очага напряженно-деформированного состояния горных по поз. 43 - пикеты наблюдений на профиле. По оси Оу - дана градация скорости счета ЕИЭМПЗ в импульсах в секунду. Рассмотрим аномальный график (поз. 42) на фиг. 11, который можно приурочить к очагу напряженно-деформированного состояния горных пород аппроксимированного моделью вертикального пласта 23 (фиг. 5) неограниченного по глубине. Для расчета воспользуемся формулами (44). По виду кривой определяем, что пласт имеет наклон. Для определения угла наклона пластов и векторов плотности тока авторами также выведены формулы, но не приводятся в настоящем изобретении из-за их громоздкости. Определим параметры кривой для левой ветви графика 26, 27 (фиг. 6): Xz1/2=0,65 см; Xz1/4=0,85 см; для правой ветви графика 26, 27 (фиг. 6): Xz1/2=0,45 см; Xz1/4=0,65 см. Из этих данных по формулам (44) получаем: для левой ветви графика: hвк=0,23 см=2,3 м; b=0,6 см=6 м; для правой ветви графика: hвк=0,24 см=2,4 м b=0,38 см=3,8 м. Осредняя результаты по двум ветвям, аномальной кривой получим: hвк=0,24 м=5,1 м. Параметры определены с точностью: Mhвк=0,005; Mh=0,08. На фиг. 12 обозначены - поз. 44 - очаг напряженно-деформированного состояния горных пород; поз. 45 - вектор плотности тока (равнозначен поз. 4). На фиг. 12 буквами обозначены - p - вектор плотности тока 45, 4. Таким образом, мы вычислили, что данный очаг напряженно-деформированного состояния горных пород (фиг. 12, поз. 44) приурочен к разрывному нарушению с глубиной залегания верхней кромки 2,4 метра и горизонтальной мощностью 10 метров. Используя вышеуказанные методы можно определять положение очагов механических напряжений связанных с разломными зонами, сейсмическими явлениями, оползневыми деформациями, обвалами и другими геодинамическими явлениями. род; p - вектор плотности тока 40, 4; b – горизонтальная мощность очага напряженно-деформированного состояния горных пород. Очаг напряженно-деформированного состояния горных пород (поз. 39) изображен на фиг. 10 и совмещен с инженерно-геологическим разрезом построенным в результате инженерно-геологических изысканий на участке. По форме графика видно, что вектор плотности тока (поз. 40, 4) направлен вертикально вниз. Центр тяжести очага совпадает с пространственным положением плоскостей скольжения оползневого тела (поз. 41). На фиг. 11 изображены - поз. 42 - аномальная кривая вертикальной составляющей ЕИЭМПЗ; 8 28474 Фиг. 1 Фиг. 2 9 28474 Фиг. 3 Фиг. 4 10 28474 Фиг. 5 Фиг. 6 Фиг. 7 11 28474 Фиг. 8 Фиг. 9 Фиг. 10 12 28474 Фиг. 11 Фиг. 12 __________________________________________________________ ДП "Український інститут промислової власності" (Укрпатент) Україна, 01133, Київ-133, бульв. Лесі Українки, 26 (044) 295-81-42, 295-61-97 __________________________________________________________ Підписано до друку ________ 2002 р. Формат 60х84 1/8. Обсяг ______ обл.-вид. арк. Тираж 34 прим. Зам._______ ____________________________________________________________ УкрІНТЕІ, 03680, Київ-39 МСП, вул. Горького, 180. (044) 268-25-22 ___________________________________________________________ 13
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determination of depth of bedding and geometrical parameters of radiating foci of rocks
Автори англійськоюSalomatin Valerii Mykolaiovych, Bezsmertnyi Andrii Fylymonovych
Назва патенту російськоюСпособ определения глубины залегания и геометрических параметров излучающих очагов горных пород
Автори російськоюСаломатин Валерий Николаевич, Бессмертный Андрей Филимонович
МПК / Мітки
Мітки: порід, параметрів, визначення, випромінюючих, залягання, глибини, осередків, гірських, спосіб, геометричних
Код посилання
<a href="https://ua.patents.su/13-28474-sposib-viznachennya-glibini-zalyagannya-ta-geometrichnikh-parametriv-viprominyuyuchikh-oseredkiv-girskikh-porid.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення глибини залягання та геометричних параметрів випромінюючих осередків гірських порід</a>
Попередній патент: Ширококутний приціл
Наступний патент: Варіатор ведучого колеса велосипеда
Випадковий патент: Фільтрувальна тканина