Спосіб matнcad-моделювання оптимально дисперсійних аналізаторів спектра короткочасних низькочастотних сигналів

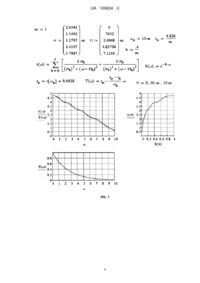
Реферат: Спосіб Mathcad-моделювання оптимально дисперсійних аналізаторів спектра короткочасних низькочастотних сигналів, у якому використовують Mathcad-модель для складання таблиці параметрів і нулів поліномів Гурвиця, яка має постійне значення масштабу m . Мathcad-модель масштабують - змінюють масштаб m . Одержують корекцію спектральної функції відгуку дисперсійної лінії затримки (ДЛЗ), зменшення кількості її секцій та часу відхилення фізичного об'єкта від нормальної безперервної роботи. Дослідженнями у Mathcad самої ДЛЗ графічним методом трьох площин одержують необхідні характеристики потрібного оптимально дисперсійного аналізатора спектра. UA 100634 U (54) СПОСІБ MATHCAD-МОДЕЛЮВАННЯ ОПТИМАЛЬНО ДИСПЕРСІЙНИХ АНАЛІЗАТОРІВ СПЕКТРА КОРОТКОЧАСНИХ НИЗЬКОЧАСТОТНИХ СИГНАЛІВ UA 100634 U UA 100634 U 5 10 15 20 25 30 35 40 45 50 55 Корисна модель належить до вимірювальної техніки аналізу частотного спектра електричних сигналів і призначена для скорочення часу відхилення реального фізичного об'єкта від нормальної безперервної роботи. За аналогією з поняттям частотних фільтрів, на відміну від вузько-смугових сигналів, низькочастотними (НЧ) називають такі сигнали, основна смуга спектральних частот яких зосереджена достатньо близько до початку координат і може мати також і нульову частоту. Відома велика кількість прикладів досить корисного використання результатів спектрального аналізу саме НЧ сигналів [Кадук Б.Г., Круковський-Синевич К.Б, Садовський В.В. Спектральний аналіз із стисненням масштабу часу. - К.: "Техніка", 1968]. Особливе значення у розробці ефективних вимірювальних систем мають різні аналізатори спектра, основним блоком, що аналізує, є дисперсійна лінія затримки (ДЛЗ). Відомі переваги та недоліки дисперсійних аналізаторів спектра [Тверской В.И. Дисперсионно-временные методы измерения спектров радиосигналов. - М: "Советское радио", 1974]. До основного з недоліків таких аналізаторів належить неможливість реалізації ДЛЗ на фазових контурах при використанні їх для аналізу спектра саме НЧ сигналів. Крім того у цих методах основну увагу приділено точності одержання прямого перетворення Фур'є при використанні так названої гіпотетичної-ідеальної ДЛЗ. Шляхом математичного моделювання у Mathcad при рівномірній апроксимації функції групового часу затримання (ГЧЗ) секцій НЧ ДЛЗ на фазових контурах одержана таблиця параметрів та нулів поліномів Гурвиця [Туник В.Ф. Пристрій табульованих секцій дисперсійних ліній затримки нижчих частот на фазових контурах. Патент на корисну модель № 72061. Бюл. № 15 від 10.08.2012]. Ця модель містить аналітичні вирази та параметри лінійної функції ГЧЗ T() лінії і функції апроксимації ГЧЗ t() , площину з графіками цих функцій, площину з графіком виділених екстремумів відхилення цих функцій і площину з функцією чебишевського альтернанса. Однак ці аналізатори є наслідком також принципу одержання за заданої функції діяння точного прямого перетворення Фур'є, що не реально. Технічною задачею, яка вирішується корисною моделлю, є задача обґрунтування шляхом моделювання у Mathcad можливості використання відомого графічного методу трьох площин реального дисперсійного аналізу за заданої спектральної функції діяння ДЛЗ при відповідному коректуванні спектральної функції відгуку ДЛЗ, зменшенні кількості секцій ДЛЗ і, як наслідок, зменшення часу відхилення фізичного об'єкта від нормальної безперервної роботи, а також розробки оптимально дисперсійних аналізаторів спектра короткочасних НЧ сигналів. Цю задачу вирішують способом Mathcad-моделювання оптимально дисперсійних аналізаторів спектра короткочасних низькочастотних сигналів, у якому використовують вище відмічену Mathcad-модель для складання таблиці параметрів і нулів поліномів Гурвиця, яка має постійне значення масштабу m . Новим є те, що цю Mathcad-модель масштабують - змінюють масштаб m , що дозволяє вирішення вказаної задачі, а дослідженнями у Mathcad самої ДЛЗ графічним методом трьох площин одержують необхідні характеристики потрібного оптимально дисперсійного аналізатора спектра, одна з цих площин має графіки лінійної функції ГЧЗ T() лінії та функції апроксимації t() функції T() , нижче першої площини розташовують другу площину з графіком спектральної функції S() сигналу впливу на ДЛЗ, а з правої сторони від першої площини розташовують третю площину, на якій одержують спектральну функцію S() сигналу відгуку ДЛЗ, де  - не спектральна частота, а спектральний час і у одержаній таким чином моделі використовують аналітичний вираз   0,.01 ..10m вектора ранжируваної змінної, у якому .01 m m - крок цього вектора, а 10m - граничне значення потрібного діапазону зміни усіх графіків, а  також використовують у цій моделі аналітичний вираз O()  2n функції оптимізації, 2   2 яка є функцією ГЧЗ n однакових фазових контурів першого порядку, параметри n і  яких визначають додатковою таблицею. На фіг. 1, що додається, наведена Mathcad-модель для дослідження дисперсійних аналізаторів графічним методом трьох площин, а на фіг. 2 - Mathcad-модель для дослідження оптимально дисперсійних аналізаторів спектра. Відомості, які підтверджують можливість та необхідність здійснення запропонованого способу полягає у тому, що Mathcad-модель фіг. 1 показана на прикладі секції ДЛЗ дев'ятого порядку. Перша площина представляє графіки функції ГЧЗ t() - суцільний графік та функції 1 UA 100634 U 5 10 15 ГЧЗ T() - пунктирний графік. Друга площина відображає графік спектральної функції S() сигналу впливу і на третій площині з розгорткою вектором   0,.01 ..10m одержується m спектральна функція S() відгуку ДЛЗ, де  - спектральний час. Важливо відзначити, що усі графіки фіг. 1 залежать від значення масштабу m так, що при зміні цього значення у сторону збільшення або зменшення усі графіки зберігають своє призначення. Цю особливість моделі фіг. 1 можна умовно назвати принципом керованості моделі при масштабуванні, коротко - принципом масштабування. Для підготовки до використання моделі фіг. 1 потрібно активізувати таблицю параметрів та нулів поліномів Гурвиця необхідної секції ДЛЗ. Після цього треба із стовпця "Початкова координата t н " цієї таблиці підставити значення координати t н у чисельник формули для цієї координати. В даному випадку - 4.826… Одержимо формулу t н  4.826 / m . Із стовпця "Відносна погрішність L / t н " цієї ж таблиці визначити значення мінімального відхилення вирівняних максимумів L - абсолютна похибка, яка у даному випадку дорівнює приблизно 0.1. На фіг. 2 показана модель оптимально дисперсійного аналізу. Ця модель одержується шляхом уведення у модель фіг. 1 функцію ГЧЗ, що оптимізує.  Ця функція O()  2n є функцією ГЧЗ фазових контурів першого порядку при їх 2   2 кількості n і значенні  згідно з наступною таблицею: Таблиця Оптимальні секції ДЛЗ Початкові параметри Порядок базової секції 5 7 9 11 13 15 tн tВ 2.4 3.63 4.826 6.0015 7.126 8.45 0.509 0.577 0.643 0.709 0.801 0.788 Одержані параметри L  tн 0.02 0.021 0.021 0.02 0.017 0.02 3.592 3.627 3.641 3.653 3.826 3.376 n 8 9 10 11 12 13 tм 6.85 8.59 10.32 12.02 13.4 16.15 L tм 0.0072 0.0091 0.0097 0.01 0.009 0.011 Нормована частота ωВ=10 рад/с 20 25 30 35 В результаті додавання функції O() до функції t() одержується суцільний графік результуючої функції ГВЗ f () на першій площині. В результаті проеціювання графіка спектральної функції S() другої площини на графік функції f () першої площини одержується відповідний графік спектральної функції f () на третій площині фіг. 2 з розгорткою вектором   0,.01 ..10m . m Із порівняння графіків на третій площині фіг. 1 і фіг. 2 виходить, що використання секції ДЛЗ, що оптимізує, в даному випадку - чотирьох фазових контурів першого порядку, які легко настроювати, одержується двократний виграш у ширині спектральної функції f () на виході ДЛЗ аналізатора і це не є межею. Однак це одержано за рахунок відповідної, але допустимої, зміни форми спектральної функції S() . Таким чином, особливості запропонованих моделей не можуть істотно впливати на його реальну корисність, бо критерій оптимальності, взагалі, є умовним і не може, як правило, визначатися тільки теорією використання методу. Частіше критерій оптимальності визначається призначенням системи і глибоким розумінням розробником результатів критичного аналізу умов її роботи. Як відомо при розв'язанні великої кількості практичних задач можна указати цілу групу доцільних критеріїв з більш чи менш доскональною теорією, вибір же конкретного критерію оптимальності визначається складністю синтезованої системи і, головне, степені доскональності теорії для її одержання. Оскільки запропоновані моделі для розробки оптимально дисперсійних аналізаторів спектра короткочасних НЧ сигналів мають порівняно великі потенційні можливості, то можна надіятися 2 UA 100634 U на успішне упровадження цих аналізаторів у науку і техніку для скорочення часу відхилення реального фізичного об'єкта від нормальної безперервної роботи. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 5 10 Спосіб Mathcad-моделювання оптимально дисперсійних аналізаторів спектра короткочасних низькочастотних сигналів, у якому використовують Mathcad-модель для складання таблиці параметрів і нулів поліномів Гурвиця, яка має постійне значення масштабу m , який відрізняється тим, що цю Mathcad-модель масштабують - змінюють масштаб m , при цьому одержують корекцію спектральної функції відгуку дисперсійної лінії затримки (ДЛЗ), зменшення кількості її секцій та часу відхилення фізичного об'єкта від нормальної безперервної роботи, а дослідженнями у Mathcad самої ДЛЗ графічним методом трьох площин одержують необхідні характеристики потрібного оптимально дисперсійного аналізатора спектра, одна з цих площин має графіки лінійної функції групового часу затримки (ГЧЗ) T() лінії та функції апроксимації 15 t() 20 T() , нижче першої площини розташовують другу площину з графіком спектральної функції S() сигналу впливу на ДЛЗ, а з правої сторони від першої площини розташовують третю площину, на якій одержують спектральну функцію S() сигналу відгуку ДЛЗ, де  - не спектральна частота, а спектральний час, і у одержаній таким чином моделі використовують аналітичній вираз   0,.01 ..10m вектора ранжируваної змінної, у якому .01 m m крок цього вектора, а 10m - граничне значення потрібного діапазону зміни усіх графіків, а також  використовують у цій моделі аналітичний вираз O()  2n 2 функції оптимізації, яка є   2 функцією ГЧЗ n однакових фазових контурів першого порядку, параметри n і  яких визначають додатковою таблицею. функції 3 UA 100634 U 4 UA 100634 U Комп’ютерна верстка Л. Ціхановська Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 5