Спосіб криптографічного перетворення двійкових даних

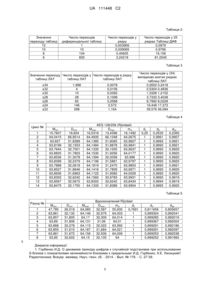
Реферат: Винахід належить до області обчислювальної техніки, а саме до способів криптографічного перетворення даних. Спосіб шифрування двійкових блоків даних, який складається з виконання за допомогою набору підключів, сформованих з майстра-ключа, ітеративної процедури криптографічних перетворень, яка складається з первинного забілювання вихідного блока даних за допомогою додавання за модулем 2 з першим підключем та наступних ітеративних циклових перетворень, кожне з яких включає розбивку вхідного блока даних на 32-бітні підблоки, котрі обробляються за допомогою операцій ByteSub, ShiftRows і AddRoundKey, на UA 111448 C2 (12) UA 111448 C2 вході всіх циклів після операції забілювання перед заходом в S-блоки першого циклу вводиться операція змішування 32-бітних сегментів вхідного блока даних по три і чотири між собою, так що замість першого 32-бітного сегмента формується сума за модулем два першого, другого та третього сегментів, замість другого 32-бітного сегмента формується сума за модулем два другого, третього та четвертого сегментів, замість третього 32-бітного сегмента формується сума за модулем два третього, четвертого та першого сегментів, замість четвертого 32-бітного сегмента формується сума за модулем два третього, четвертого, першого та другого сегментів і далі виконуються штатні операції шифру Rijndael. Технічним результатом, що досягається даним винаходом, є підвищення надійності та захисту шифрування від криптоаналітичних та алгебраїчних атак, без помітного зниження швидкодії. UA 111448 C2 5 10 15 20 25 30 35 40 45 50 55 Винахід належить до області обчислювальної техніки, а саме до способів криптографічного перетворення даних. Відомі способи криптографічних перетворень даних з використанням при формуванні циклових функцій множення виходів набору байтів на МДР матриці (шифри Rijndael, Калина, ADE, IDEA NXT та інші), яке дозволяє реалізувати стратегію широкого сліду. Ці конструкції циклових перетворень при активізації одного байта на вході шифру дають можливість активізувати на першому циклі тільки один S-блок циклової функції, що приводить до того, що на другому циклі вдається активізувати у шифрі Rijndael тільки чотири S-блоки, а на третьому циклі вже 16-ть S-блоків. В результаті для приходу шифру Rijndael до стану випадкової підстановки по диференціальних та лінійних показниках для 128 бітного шифру затрачується 4-й цикл. Аналогічна ситуація має місце і для інших шифрів, що призводить до того, що відомі шифри приходять до стану випадкової підстановки за чотири і більше циклів. Найбільш близьким за сукупністю суттєвих ознак до способу, який заявляється, є спосіб, реалізований у шифрі Rijndael (AES) (див. J. Daemen and V. Rijmen. AES Proposal: Rijndael. 1st AES Conference, California, USA, 1998. http://www.nist.gov/aes). котрий полягає у виконанні багатоциклової процедури криптографічних перетворень, які виконуються за допомогою набору підключів і складається з первинного забілювання вихідного блока даних за допомогою додавання за модулем 2 з першим підключем та наступних ітеративних циклових перетворень, кожне з яких включає розбивку вхідного блока даних на 32-ох бітні сегменти, які подаються на входи четвірок байтових S-блоків (операції ByteSub), виходи яких піддаються фіксованим зрушенням на визначене число байтів (операція ShiftRow), після чого заново сформовані четвірки байтів обробляються за допомогою множення на МДР матриці розміром 44 (операції MixColumn), і об'єднані результати множення підсумовуються з цикловим підключем за модулем два, причому в останньому циклі використовуються тільки операції ByteSub і ShiftRow з заключним додаванням за модулем 2 останнього циклового підключа (операція AddRoundKey). Недоліком цього способу є по-перше низькі динамічні показники приходу шифру до стану випадкової підстановки (шифр приходить до стану випадкової підстановки за чотири цикли), і по друге алгебраїчна структура використаних в шифрі S-блоків відмічається в ряді публікацій як потенційна слабкість (вона може бути використана для побудування алгебраїчної атаки на шифр, однак на теперішній час складність цієї атаки залишається занадто високою), а використання S-блоків випадкового типу (з більш високими значеннями диференційних та лінійних ймовірностей) призводить до збільшення до п'яти числа циклів, потрібних шифру для приходу до стану випадкової підстановки. Технічною задачею винаходу є створення способу криптографічного перетворення двійкових даних з покращеними динамічними показниками приходу шифру до стану випадкової підстановки й забезпечення можливості використання у шифрі випадкових S-блоків без помітного зниження швидкодії. Набуття шифром асимптотичних значень максимумів диференційних та лінійних ймовірностей характеризує момент, з якого шифр досягає потенційних показників стійкості. Отже більш швидкий прихід шифру до стану випадкової підстановки означає підвищений рівень його стійкості до відомих криптоаналітичних атак, а використання випадкових S-блоків забезпечує підвищений захист від потенційних алгебраїчних атак. Зазначена задача вирішується наступнім чином. У способі шифрування двійкових блоків даних, який складається з виконання за допомогою набору підключів, сформованих з майстраключа, ітеративної процедури криптографічних перетворень, яка включає первинне забілювання вихідного блока даних за допомогою додавання за модулем 2 з першим підключем та наступних ітеративних циклових перетворень, кожне з яких містить розбивку вхідного блока даних на 32-ох бітні підблоки, котрі обробляються за допомогою операцій ByteSub, ShiftRow і AddRoundKey, причому в останньому циклі використовуються тільки операції ByteSub і ShiftRow з заключним додаванням за модулем 2 останнього циклового підключа (операція AddRoundKey), відповідно винаходу, після операції забілювання перед заходом в S-блоки першого циклу вводиться операція змішування 32-ох бітних сегментів вхідного блока даних по три і чотири між собою, так що замість першого 32-ох бітного сегмента формується сума за модулем два першого, другого та третього сегментів, замість другого 32-ох бітного сегмента формується сума за модулем два другого, третього та четвертого сегментів, замість третього 32-ох бітного сегмента формується сума за модулем два третього, четвертого та першого сегментів, замість четвертого 32-ох бітного сегмента формується сума за модулем два третього, четвертого, першого та другого сегментів і далі виконуються штатні операції шифру Rijndael. 1 UA 111448 C2 5 10 15 20 Перерахована сукупність істотних ознак дозволяє реалізувати початкове циклове перетворення, що має поліпшені перемішуючі та розсіюючі властивості і за рахунок цього забезпечити можливість використання у шифрі випадково породжених S-блоків без зниження показників криптографічної стійкості. Запропонований спосіб може бути реалізований за допомогою пристроїв, з'єднання між якими ілюструє блок-схема, де: 1 - накопичувач відкритого тексту, підключений своїм виходом до першого входу суматора 2 за модулем два, на другий вхід котрого підводиться ключ забілювання з виходу регістра-накопичувача циклових підключів 3, до виходу суматора підключений блок змішування сегментів даних 4, далі йде блок восьмициклового зашифрування основного варіанта шифру Rijndael 5, вихід котрого підключений до накопичувача-формувача зашифрованого блока даних 6. Далі обговорюються властивості випадковості запропонованого рішення. Показники випадковості шифру, побудованому за запропонованим способом. У цьому розділі ми наведемо результати оцінки очікуваних параметрів переходу шифру до стану випадкової підстановки. У відповідності з ідеєю розвинутого в [1] підході необхідно виконати оцінку мінімального числа активних (задіяних S-блоків), після проходження яких шифр стає випадковою підстановкою. Це мінімальне число визначається диференціальними та лінійними показниками самих S-блоків, застосованих у шифрі, конструкціями і властивостями його циклових перетворень, а також значеннями показників доказовою стійкості шифру, що залежать від розміру його бітового входу. В роботі [1] цей зв'язок між зазначеними показниками визначений у вигляді двох співвідношень:    IPS D  (DPmax )k , IPS L  2k 1  LPmax  Тут DPmax 25  і LPmax  . (1) k - максимальні значення диференціальної і лінійної ймовірностей підстановлювальних перетворень ( x ) . IPSD (Диференціальний Індикатор доказової безпеки) диференційний показник доказової безпеки і 30 35 40 45 50 55 IPS L (Linear Indicator of Provable Security) лінійний показник доказової безпеки, k  k min - мінімальне число активних S-блоків, що беруть участь у формуванні переходу шифру до випадкової підстановки. Тут ми будемо орієнтуватися на 128 бітний шифр. Користуючись розрахунковими і співвідношеннями, встановленими в роботі [6], можна прийти до висновку, що очікуване значення максимуму диференціального переходу для шифру з 128-ми бітним входом виявляється близьким до 121, а очікуване значення максимуму 67 зміщення лінійного корпусу для шифру з 128 бітним входом виявляється близьким до 2 . Відповідно отримаємо, що максимальні значення лінійної та диференціальної ймовірності для -120 -121 шифру з 128 бітним входом виходять близькими одне до одного і рівними приблизно 2 2 (близькими до складності атаки повного перебору ключів). Виходячи з наведених вище співвідношень можна зробити висновок, що для шифру з 128 бітним входом потрібно для приходу до стану випадкової підстановки за диференціальними переходами при використанні S-блоків шифру Rijndael з граничними показниками   рівномірності, рівними DPmax  2 6 (відповідно до рівності 2 120  (2 6 )k )k min =20 активних Sблоків. Аналогічно, для приходу до стану випадкової підстановки за лінійними показниками при  використанні S-блоків з граничними показниками не лінійності, рівними LPmax  2 6 буде потрібно використати відповідно до рівняння 2 121  2k 1  (2 6 )k k min =24 активних S-блоків. Звернемо тепер увагу на те, що в нашому шифрі додатково введена операція змішування 32-х бітних сегментів вхідного блока даних, що отримані після його підсумування за модулем два з першим цикловим підключем (операції забілювання). Ця додаткова операція дозволяє активізувати на першому циклі одразу мінімум три S-блоки (активізується у гіршому випадку одразу три SL перетворення по одному байту в кожному), а за два цикли байти входу пройдуть мінімум через 3+12=15 S-блоків. На трьох циклах це вже буде, якщо рахувати, що на ньому вдасться активізувати 16-ть S-блоків) 15+16=31 активний S-блок. Це означає, що для S-блоків з граничними диференціальними та лінійними показниками   (для S-блоків шифру Rijndael з DPmax  LPmax  2 6 ) пропонований шифр приходить до випадкової підстановки за три цикли і за диференційними і за лінійними показниками. Наведемо тут реальні показники активізації S-блоків перших циклів. 2 UA 111448 C2 5 10 15 20 Результати експериментів ілюструє таблиця 1. У цій таблиці наведені кількості активних Sблоків на відповідних циклах при активізації одного байта входу. Таблиця починається з двох циклів. Легко впевнитись, що на першому циклі активізується одним байтом три чи чотири Sблоки. В той же час починаючи з третього циклу як у шифрі Rijndael, так і в його вдосконаленої версії активізується мінімум 13 S-блоків. Отже реально на трьох циклах вдається активізувати 15+13=28 S-блоків, що не змінює раніше зроблений висновок стосовно приходу вдосконаленого шифру до стану випадкової підстановки за три цикли. Оцінка можливостей використання в шифрі випадкових S-блоків. Оцінимо перспективи використання в шифрі випадкових S-блоків. Методика виконання розрахунків представлена в роботі [1]. У табл. 2 наведені результати розрахунків числа переходів різного типу в 25-ти рядках диференціальної таблиці випадкової підстановки. В розрахунках одразу взята орієнтировка на мінімальне число активних S-блоків випадкового типу для трьох циклів шифру що дорівнює 25. З представлених результатів випливає, що для активних S-блоків при виборі в рядках максимально ймовірних переходів можна очікувати при випадкових входах в S-блоки: один перехід зі значенням 10; десять переходів із значенням 8; чотирнадцять переходів із значенням 6. Всього 25 переходів (25 активних S-блоків). Обчислення в цьому випадку призводять до результату: 10 10  8   6      256  256   256  25 30 35 40 14  2 130 . Це означає, що випадкові S-блоки для цього шифру забезпечують з запасом за три цикли його прихід за диференціальними показниками до стану випадкової підстановки. Наведемо тепер розподіл переходів для зміщень лінійної апроксимаційної таблиці. У загальне число переходів тут входять і позитивні і негативні зміщення. Користуючись результатами робот [1, 2], можемо розрахувати числа переходів різного типу в 31-му рядку лінійної апроксимаційної таблиці випадкової підстановки, підсумки розрахунків яких представлені в табл. 3. Знову будемо вважати, що за рахунок введення циклових підключів входи в S-блоки будуть випадковими і статистично незалежними. Методика розрахунків представлена в роботах [1, 2]. У таблиці представлені результати оцінки числа переходів і їх значень в 31-ому випадково взятих рядках таблиці ЛАТ. З результатів випливає, що для 31-го активного S-блока при використанні максимально ймовірних переходів можна очікувати при випадкових входах у випадкові S-блоки: один перехід зі значенням 30; три переходи зі значенням 28; вісім переходів зі значенням 26; сімнадцять переходів зі значенням 24; один перехід зі значенням 22. Усього разом з першим найбільш ймовірним переходом зі значенням 34 - це є 31 перехід. Вважаючи далі, що рядки в S-блок вибираються з усієї множини з 256-ти рядків, при цьому переходи по S-блоках йдуть в довільному порядку і здійснюються за найбільш ймовірним шляхом, можемо виконати оцінку ймовірності приходу шифру до стану випадкової підстановки з випадковими S-блоками. Обчислення для значення k  31 призводять до результату 3 45 50 2 311 8 17 2 2 2 2 2 2  34   30    28     26     24             22   2 115            128   128    128     128     128    128        і, отже, 31-ий активний S-блок не дозволяє здійснити перехід шифру до випадкової підстановки за лінійними показниками. Але за чотири цикли шифр з додатковим підсумуванням приходить до стану випадкової підстановки (на чотирьох циклах буде активними мінімум 44-і Sблоки). Нагадаємо на закінчення, що шифр Rijndael приходить до стану випадкової підстановки за диференціальними показниками на третьому циклі, а за лінійними показниками лише на четвертому, причому для приходу до стану випадкової підстановки з випадковими S-блоками йому потрібно буде задіяти п'ять циклів (на чотирьох циклах активізується 1+4+16+13=34 Sблоки). 3 UA 111448 C2 5 10 15 20 25 Таким чином, показана можливість реалізації принципів активізації на першому циклі шифру Rijndael мінімум трьох S-блоків, на двох циклах 15-ти S-блоків, на трьох мінімум 28-м S-блоків, на чотирьох мінімум 44-х S-блоків. Шифр Rijndael, з запропонованою конструкцією доциклового перемішування 32-ох бітних сегментів входу стає випадковою підстановкою на четвертому циклі за диференційними і за лінійними показниками і при використанні випадкових S-блоків. Оцінка продуктивності запропонованого винаходу. Як і в роботі [3], при оцінці обчислювальної складності будемо орієнтуватися на число XOR операцій, виконуваних шифром в процесі зашифрування і розшифрування. Будемо виходити з того, що для виконання SL-перетворення у вигляді матричного множення в оптимізованому варіанті шифру Rijndael, потрібно виконати 4-ри XOR операції [3]. У кожному циклі шифру Rijndael для чотирьох SL перетворень буде задіяне 16 XOR-ів. Отже десять циклів шифру потребують використання 16×9+4=148 XOR-ів (з урахуванням забілювання). Для виконання доциклового перемішування в удосконаленому шифрі потрібно буде виконати ще 9-ть XOR-ів, тобто загальна кількість XOR операцій на весь шифр складає 148+9=157-м XOR-ів, тобто продуктивність вдосконаленого шифру суттєво не зменшується (ми тут не враховуємо затрати на процедуру розгортання ключів). Головна перевага запропонованого рішення міститься у тому, що вдосконалений шифр приходить до випадкової підстановки за чотри цикли як і основна версія шифру Rijndael, однак вдосконалений шифр допускає використання в якості S-блоків підстановок випадкового типу. Для ілюстрації підвищеної ефективності запропонованого рішення за динамікою приходу шифру до стану випадкової підстановки далі у табл. 3 і табл. 4 наведені результати оцінки показників статистичної безпеки шифру Rijndael та його вдосконаленої версії. У перших п'яти стовпчиках наведені результати аналізу лавинного ефекту, реалізованого в експериментах з шифром Rijndael (табл. 4) та його вдосконаленої версії (табл. 5). В таблицях наводяться числа одиничних і нульових елементів в побітових різницях зашифрованих блоків на виході кожного циклу для пар блоків даних на вході шифру, що відрізняються одним бітом, а також показники ступеня повноти d c , ступеня лавинного ефекту d a та ступеня суворого лавинного критерію d sa [4]. 30 Практично вже на другому циклі вдосконалений Rijndael становиться випадковою підстановкою по всіх показниках. В той же час основна версія шифру становиться випадковою підстановкою лише на третьому циклі (значення mw попадає в довірчий інтервал 64  0,1861  m w  64  0,1861 [4] на третьому циклі). Таблиця 1 Число активних S-блоків 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 2-й цикл AES зi AES складанням 0 0 0 0 0 0 0 0 65280 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 48960 0 0 0 0 0 0 0 16320 3-й цикл AES зi AES складанням 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 100 0 3885 65280 61292 35 4 4-й цикл АЕБ зі AES складанням 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 119 ПО 3883 3815 61275 61351 UA 111448 C2 Таблиця 2 Значення переходу таблиці 12 10 8 6 Число переходів диференціальної таблиці 1 10 104 830 Число переходів у рядку 0,003906 0,039065 0,40625 3,24218 Число переходів у 25 рядках Таблиці ДИФ 0,0979 0,9766 19,156 81,0545 Таблиця 3 Значення переходу Число переходів у Число переходів в рядку таблиці ЛАТ таблиці ЛАТ таблиці ЛАТ ±34 ±32 ±30 ±28 ±26 ±24 ±22 1,998 4 10 28 65 146 298 0,0078 0,0156 0,0392 0,1098 0,2588 0,572 1,164 Число переходів у (34) випадково взятих рядках таблиці ЛАТ 0,2652 0,2418 0,5304 0,4836 1,3328 1,2152 3,7332 3,4038 8,7992 8,0228 19,448 17,372 39,576 36,084 Таблиця 4 Цикл № 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Mnin 15,7607 64,0415 63,827 63,8199 63,7944 63,8825 63,8536 63,8399 63,7888 63,8527 63,8936 63,8302 63,8567 63,8475 Dmin 16,604 66,9514 31,8389 32,1553 32,7001 31,7803 31,3078 32,2379 32,0618 31,8646 31,6963 32,6242 32,5672 32,1750 AES 128/256 (Rijndael) Mmах Dmax mw 16,5318 13,4396 16,1492 64,4935 66,1048 64,2675 64,1385 31,8065 63,9827 64,1484 31,8878 63,9841 64,1330 32,1005 63,9637 64,1530 31,9256 64,0177 64,1394 32,0058 63,996 64,1196 31,5861 63,9797 64,1819 31,2470 63,9853 64,1416 31,7809 63,9971 64,1122 31,9582 64,0029 64,1560 30,9783 63,9931 63,8302 32,6242 63,8434 64,1333 31,8389 63,9904 dc 0,25 1 1 1 1 1 1 1 1 1 1 1 1 1 da 0,2533 0,9961 0,9993 0,9993 0,9993 0,9993 0,9993 0,9993 0,9993 0,9993 0,9993 0,9993 0,9994 0,9993 dsa 0,2365 0,9907 0,9921 0,9921 0,9920 0,9920 0,9920 0,9920 0,9921 0,9920 0,9920 0,9919 0,9919 0,9920 Таблиця 5 Раунд № 1 2 3 4 5 6 7 8 Мmin 47,785 63,861 63,857 63,89 63,868 63,855 63,861 63,85 Dmin 26,018 32,132 31,805 31,806 32,278 31,615 31,672 32,602 Mmax 64,085 64,146 64,17 64,131 64,115 64,187 64,156 64,15 Вдосконалений Rijndael Dmax mw dc 32,587 55,935 0,7691 32,979 64,003 1 32,309 64,014 1 31,06 64,01 1 32,022 63,992 1 31,684 64,021 1 32,506 64,009 1 32,105 64 1 da 0,811656 0,999324 0,999285 0,999367 0,999291 0,999291 0,999253 0,999252 dsa 0,805657 0,992041 0,992019 0,992004 0,992186 0,992097 0,992038 0,991993 5 Джерела інформації: 1. Горбенко И.Д. О динамике прихода шифров к случайной подстановке при использовании S-блоков с показателями нелинейности близкими к предельным/ И.Д. Горбенко, К.Е. Лисицкий// Радиотехника: Всеукр. межвед. Науч.-техн. сб. - 2014. - Вып. № 176. - С. 27-39. 5 UA 111448 C2 5 10 2. Lisitskiy K.E. On Maxima Distribution of Full Differentials and Linear Hulls of Block Symmetric Ciphers [Text]/ K.E. Lisitskiy// I.J. Computer Network and Information Security, 2014, 1, 11-18 Published Online November 2013 in MECS (http://www.mecs-press.org/) DOI: 10.5815/ijcnis. 2014.01.02. 3. Горбенко И.Д. Свойства и возможности оптимизации криптографических преобразований в AES-RIJNDAEL/ И.Д. Горбенко, Д.А. Чекалин// Радиотехника. Всеукр. Межвед. Науч.-техн. сб. 2001. Вып. 119. С. 36-42. 4. Долгов Виктор Иванович. Методология оценки стойкости блочных симметричных шифров к атакам дифференциального и линейного криптоанализа: монография./ В.И. Долгов, И.В. Лисицкая. - Харьков. Издательство "Форт", - 2013. - 420 с. ФОРМУЛА ВИНАХОДУ 15 20 25 Спосіб шифрування двійкових блоків даних, де за допомогою набору підключів, сформованих з майстра-ключа, виконують ітеративну процедуру криптографічних перетворень, яка складається з первинного забілювання вихідного блока даних за допомогою додавання за модулем 2 з першим підключем та наступних ітеративних циклових перетворень, кожне з яких включає розбивку вхідного блока даних на 32-бітні підблоки, котрі обробляють за допомогою операцій ByteSub, ShiftRows і AddRoundKey, який відрізняється тим, що на вході всіх циклів після операції забілювання перед заходом в S-блоки першого циклу вводять операції змішування 32-бітних сегментів вхідного блока даних по три і чотири між собою, так, що замість першого 32-бітного сегмента формується сума за модулем два першого, другого та третього сегментів, замість другого 32-бітного сегмента формується сума за модулем два другого, третього та четвертого сегментів, замість третього 32-бітного сегмента формується сума за модулем два третього, четвертого та першого сегментів, замість четвертого 32-бітного сегмента формується сума за модулем два третього, четвертого, першого та другого сегментів і далі виконують штатні операції шифру Rijndael. Комп’ютерна верстка Г. Паяльніков Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 6