Спосіб прогнозування розвитку складних систем
Номер патенту: 82983
Опубліковано: 27.08.2013
Автори: Горошкова Лідія Анатоліївна, Волков Володимир Петрович
Формула / Реферат
Спосіб прогнозування розвитку складних систем, що включає введення часових рядів даних щодо кількісних характеристик, їх комп'ютерну обробку і графічне представлення, визначення точності прогнозу, який відрізняється тим, що додатково здійснюють структурування системи та виокремлення її підсистем; установлюють взаємозв'язки між підсистемами складної системи; вводять кількісні значення вихідних даних в електронну таблицю; здійснюють комп'ютерну обробку даних часових рядів з використанням багатофакторної математичної моделі, на основі системи лінійних диференційних рівнянь:
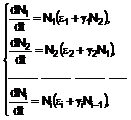
де:
![]() - кількість підсистем у складній системі, кількість;
- кількість підсистем у складній системі, кількість;
![]() - кількісна характеристика і-ї підсистеми, кількість;
- кількісна характеристика і-ї підсистеми, кількість;
![]() - коефіцієнт приросту кількісної характеристики підсистеми за умови її незалежного функціонування, безрозмірна величина;
- коефіцієнт приросту кількісної характеристики підсистеми за умови її незалежного функціонування, безрозмірна величина;
![]() - коефіцієнт приросту внутрішніх властивостей підсистеми, безрозмірна величина;
- коефіцієнт приросту внутрішніх властивостей підсистеми, безрозмірна величина;
![]() - постійна величина, що визначається внутрішніми властивостями підсистеми, безрозмірна величина;
- постійна величина, що визначається внутрішніми властивостями підсистеми, безрозмірна величина;
![]() - прирощення кількісної характеристики підсистем, що відповідає кількості взаємодій між ними, кількість,
- прирощення кількісної характеристики підсистем, що відповідає кількості взаємодій між ними, кількість,
а результати прогнозу розвитку системи і її складових отримують одночасно у табличній та графічній формі, порівнюють теоретичні й фактичні дані.
Текст
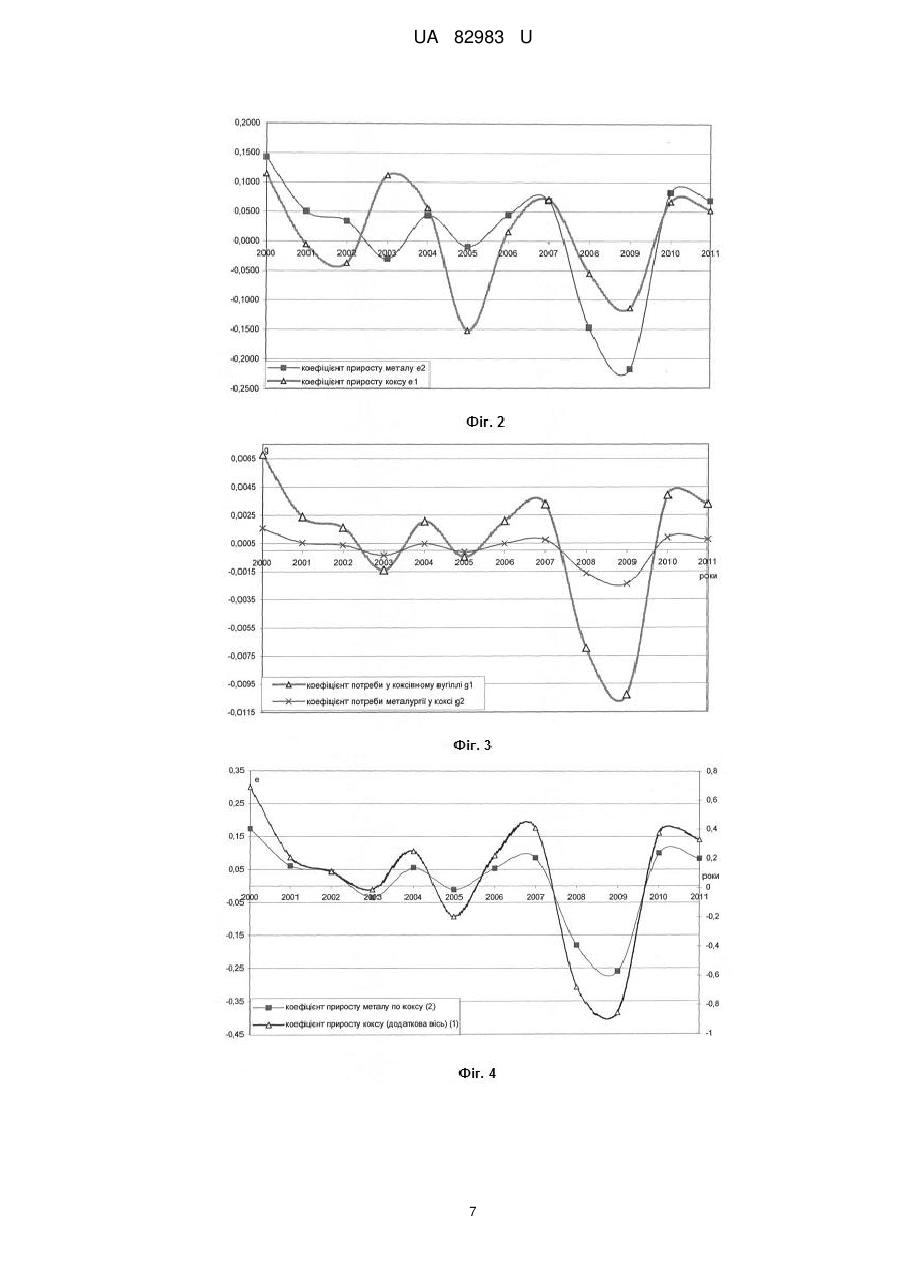
Реферат: Спосіб прогнозування розвитку складних систем включає введення часових рядів даних щодо кількісних характеристик, їх комп'ютерну обробку і графічне представлення, визначення точності прогнозу. Додатково здійснюють структурування системи та виокремлення її підсистем. Установлюють взаємозв'язки між підсистемами складної системи. Вводять кількісні значення вихідних даних в електронну таблицю. Здійснюють комп'ютерну обробку даних часових рядів з використанням багатофакторної математичної моделі. UA 82983 U (54) СПОСІБ ПРОГНОЗУВАННЯ РОЗВИТКУ СКЛАДНИХ СИСТЕМ UA 82983 U UA 82983 U 5 10 15 20 25 30 35 40 45 50 55 60 Спосіб належить до обчислювальної техніки, а саме до моделювання складних систем та може бути використаний для прогнозування динаміки складних систем з урахуванням циклічного характеру їх розвитку і взаємозв'язку підсистем. Відомі [Здрок В.В. Економетрія / Здрок В.В., Лагоцький Т.Я. - К.:3нання, 2010. - 541 с., С. 220-240] традиційні підходи до дослідження динамічних процесів з використанням трендових моделей, в яких, для зменшення коливальності ряду, використовують такі методи: 1. Згладжування ряду за допомогою середніх. Полягає в укрупненні інтервалів часу та заміні вихідного ряду - рядом середніх. 2. Аналітичне вирівнювання ряду. Здійснюють вираження головної тенденції розвитку у вигляді функції показника від часу (модель тренда). Такий підхід має певні обмеження щодо використання. Так, в економічних системах він виправданий на макрорівні, бо в процесі аналізу економічних циклів враховується той факт, що в процесі переходу від одного циклу до іншого відбувається різка зміна стану економічної системи на новий ступінь свого розвитку, тобто відбувається економічне зростання. Таким чином, у разі використання апроксимації та згладжування часових рядів даних можуть бути досліджені середні та "довгі" цикли економічного розвитку, що є характерними для макрорівня і не можуть бути вивчені процеси на мезорівні, де основними є малі цикли. Серед методів дослідження і прогнозування як статичних, так і динамічних процесів або явищ, використовують функцію Кобба-Дугласа [Наконечний С.І. Економетрія / С.І. Наконечний, Т.О. Терещенко, Т.П. Романюк. - К.: КНЕУ, 2004. - 520 с., С. 140-149], яку застосовують у стратегічному прогнозуванні, але недоліком є те, що її використовують для певного проміжку часу. Вважають, що впродовж цього відрізку часу кардинально не змінюються параметри системи, наприклад технологія виробництва, економічні умови господарювання і т. ін., тобто можна стверджувати, що параметри виробничої функції будуть знаходитись у межах допустимої похибки. У разі наявності суттєвих змін, їх необхідно враховувати і коригувати модель. Параметри виробничої функції оцінюються, в основному, методами кореляційнорегресійного аналізу [Здрок В.В. Економетрія / Здрок В.В., Лагоцький Т.Я. - К.:3нання, 2010. 541 с., С. 35-111]. Отримані в такий спосіб виробничі функції є статистичними залежностями, що відображають передбачувані тенденції розвитку об'єкта дослідження. Їх основним недоліком є можливе виникнення мультиколінеарності внаслідок лінійного взаємозв'язку між пояснювальними змінними в економетричних моделях. Існують певні методи позбавлення від мультиколінеарності [Наконечний С.І. Економетрія / С.І. Наконечний, Т.О. Терещенко, Т.П. Романюк. - К.:КНЕУ, 2004. - 520 с., С. 203-244]. Найпростіший спосіб - це відкинути одну із змінних у мультиколінеарній парі. Однак на практиці вилучення якогось чинника може суперечити логіці зв'язків у системі. Можливо також перетворити певним чином пояснювальні змінні моделі: знайти відхилення від середньої; використати не абсолютні, а відносні значення показників; нормалізувати пояснювальні змінні; використати "рідж-регресію", але це також не позбавляє цей підхід від недоліків. Відомий спосіб прогнозування та моделювання розвитку складних систем [Пат. 71851А Україна, МПК (2006) G06Q99/00 G06N7/00. Спосіб одержання якісних експертних оцінок при моделюванні економічних, соціальних, біологічних систем / Коршевнюк Л.О., Коршевнюк Д.О., Мінін М.Ю.; заявник та патентовласник Коршевнюк Л.О. - № 20031213217; заявл. 31.12.2003; опубл. 15.12.2004, Бюл. № 12.], що включає отримання реальних експертних оцінок при моделюванні економічних, соціальних і біологічних систем; комп'ютерну обробку отриманих від експертів позицій покажчика між крайніми поділками на шкалі оцінок. Недоліками цього способу є те, що моделювання економічних, соціальних і біологічних систем базується на даних експертних оцінок, що вносить суб'єктивні фактори. Унаслідок цього отримувані оцінки об'єктів не достатньою мірою реалістичні, що погіршує якість моделей та прогнозів. Крім того, зазначений спосіб дає можливість оцінити та моделювати не кількісні, а тільки якісні характеристики зазначених систем, що також є його обмеженням і недоліком. Ознаками, спільними з рішенням, що заявляється, є комп'ютерна обробка даних. Відомий спосіб прогнозування розвитку складних систем [Пат. 45536А Україна, МПК (2006) G06Q90/00. Системи прогнозування часових рядів фінансово-економічних показників / Садовніков О.О., Красін Л.А., Хоренко Ю.С., Бурдюк І.В.; заявник та патентовласник ВАТ "НВП Орбіта", Садовніков О.О., Красін Л.А., Ходоренко Ю.С., Бурдюк І.В. - № 2000074103; заявл. 11.07.2000; опубл. 15.04.2002, Бюл. № 4.], що включає введення вихідних часових рядів даних; вибирання одномірного часового ряду даних; його обробку; автоматизований комп'ютерний оптимальний вибір найкращого з існуючого переліку математичних моделей, якими є лінійна й квадратична авторегресія та степеневий поліном; прогнозування членів часового ряду за допомогою вибраної моделі; визначення похибки прогнозу. 1 UA 82983 U 5 10 15 20 25 30 35 40 Основними недоліками вищезгаданої системи прогнозування є те, що прогнозування часових рядів фінансово-економічних показників здійснюють за кожним окремим показником; відсутня можливість установлення взаємозв'язку між динамікою та характером зміни показників. Крім того, використовувані в системі прогнозування моделі передбачають апроксимацію і згладжування часових рядів аналізованих показників, що недоцільно в разі аналізу стану складних систем, що характеризуються циклічною динамікою розвитку. Спільними ознаками із рішенням, що заявляється, є введення часових рядів даних щодо кількісних характеристик, їх комп'ютерна обробка і графічне представлення, визначення точності прогнозу. В основу корисної моделі поставлено задачу розробити спосіб прогнозування розвитку складних систем, який шляхом побудови багатофакторної динамічної моделі, з урахуванням циклічності та взаємозв'язку підсистем, дозволяє отримувати якісні і кількісні оцінки стану системи та підвищує точність прогнозу незалежно від характеристик часового ряду даних. Суттєвими ознаками рішення, що заявляється, є: - структурування системи з виокремленням її підсистем; - установлення взаємозв'язку між підсистемами складної системи; - введення часових рядів даних щодо кількісних характеристик складної системи та її підсистем для прогнозування в електронну таблицю; - комп'ютерна обробка даних часових рядів з використанням багатофакторної математичної моделі на основі системи лінійних диференційних рівнянь: dN1 dt N11 1N2 , dN2 N N , 2 2 2 1 (1) dt .......... .......... .......... ...... dNi dt Ni i iNi 1 , де i - кількість підсистем у складній системі, кількість; Ni - кількісна характеристика і-ї підсистеми, кількість; i - коефіцієнт приросту кількісної характеристики підсистеми за умови її незалежного функціонування, безрозмірна величина; dN1 dt N11 1N2 , dN2 N N , 2 2 2 1 - коефіцієнт приросту внутрішніх властивостей підсистеми, dt .......... .......... .......... ...... dNi dt Ni i iNi 1 , безрозмірна величина; - постійна величина, що визначається внутрішніми властивостями підсистеми, безрозмірна величина; i - прирощення кількісної характеристики підсистем, що відповідає кількості взаємодій між ними, кількість; - формування результатів прогнозу розвитку системи та її складових одночасно в табличній та графічній формах; - порівняння теоретичних та фактичних даних із визначенням точності оцінки. Відмінними від прототипу ознаками є: - структурування системи та виокремлення її підсистем; - установлення характеру взаємозв'язку між підсистемами складної системи; - введення даних для прогнозування в електронну таблицю; - комп'ютерна обробка даних часових рядів з використанням багатофакторної математичної моделі на основі системи лінійних диференційних рівнянь 1; - отримання результатів прогнозу розвитку системи та її складових одночасно в табличній та графічній формі; - порівняння теоретичних та фактичних даних. 2 UA 82983 U 5 10 15 20 25 30 35 40 Перевагами рішення, що пропонується, є: - використання як дискретних, так і безперервних числових рядів; - здійснення обробки даних часових рядів з використанням багатофакторної математичної моделі, в якій відсутня потреба у вибиранні одномірного часового ряду даних і необхідності позбуватися можливої мультиколінеарності між рядами даних щодо факторних ознак; - використання системи лінійних диференційних рівнянь замість моделей лінійної й квадратичної авторегресії та степеневих поліномів, що дозволяє враховувати циклічний характер процесів у складних системах; - використання моделі, що дозволяє описати не тільки динамічні процеси розвитку окремих підсистем складних економічних систем, а й розширює її функціональні можливості для урахуванням циклічності взаємозв'язку між підсистемами; - зменшення кількості розрахункових операцій для досягнення кінцевого результату; - зменшення кількості можливих моделей для прогнозування; - відсутність багатоваріантних ітерацій при отриманні результату. Сутність рішення пояснюється кресленнями та описом математичної моделі й алгоритмом реалізації способу прогнозування: - на Фіг. 1 - зображено блок-схему способу прогнозування; - на Фіг. 2 - наведено динаміку коефіцієнтів приросту виробництва коксу і продукції чорної металургії у випадку відносної самостійності галузей; - на Фіг. 3 - наведено динаміку приросту споживання коксу в чорній металургії; - на Фіг. 4 - наведено динаміку коефіцієнтів приросту виробництва коксу і чорних металів для випадку взаємозв'язку галузей. Теоретичною основою математичного опису періодичного характеру розвитку складної системи є функція: dN=N dt, (2) де: - постійний коефіцієнт пропорційності, що виражає відношення швидкості приросту значення показника dN до N, безрозмірна величина. dt Для декількох взаємозалежних підсистем, коефіцієнти приросту 1 dN у загальному випадку N dt залежать від значення величини і часу. Вони описуються системою лінійних диференціальних рівнянь 1. Враховуючи, що не введено ніяких обмежень щодо знаків коефіцієнтів приросту і , виникає досить велика кількість ймовірних випадків знаків для цих величин. У розглянутому випадку одна з підсистем характеризується деяким коефіцієнтом приросту 1, який є постійним і позитивним (1>0) за умови ізольованого існування підсистеми. Інша підсистема в разі ізольованого існування, має коефіцієнт приросту - 2, що є постійним і від'ємним (2
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for predictive modeling of complex system development
Автори англійськоюVolkov Volodymyr Petrovych, Horshkova Lidia Anatoliivna
Назва патенту російськоюСпособ прогнозирования развития сложных систем
Автори російськоюВолков Владимир Петрович, Горошкова Лидия Анатольевна
МПК / Мітки
МПК: G06Q 10/06, G06Q 90/00
Мітки: систем, складних, прогнозування, спосіб, розвитку
Код посилання
<a href="https://ua.patents.su/10-82983-sposib-prognozuvannya-rozvitku-skladnikh-sistem.html" target="_blank" rel="follow" title="База патентів України">Спосіб прогнозування розвитку складних систем</a>
Попередній патент: Спосіб виготовлення світловипромінюючого діода на основі нанокомпозитної органо-неорганічної гетероструктури
Наступний патент: Спосіб профілактики розвитку алергічних реакцій на акрилові базиси знімних протезів
Випадковий патент: Гнучкий еластичний волоконнозміцнений удароміцний матеріал