Спосіб формування і перевірки достовірності колективного електронного цифрового підпису для засвідчення електронного документа
Номер патенту: 31105
Опубліковано: 25.03.2008
Автори: Карпуков Леонід Матвійович, Молдов'ян Олександр Андрійович, Козіна Галина Леонідівна, Молдов'ян Микола Андрійович
Формула / Реферат
1. Спосіб формування і перевірки достовірності колективного електронного цифрового підпису для засвідчення електронного документа, який полягає в тому, що генерують сукупність з n > 2 секретних ключів у вигляді багаторозрядних двійкових чисел k1, k2, ..., kn, по секретних ключах формують n відкритих ключів Р1, Р2, ..., Рn, відповідно, приймають принаймні один електронний документ, представлений багаторозрядним двійковим числом H, залежно від прийнятого електронного документа і від значення принаймні одного секретного ключа формують колективний електронний цифровий підпис Q у вигляді двох або більше багаторозрядних двійкових чисел, формують перше А і друге В перевірні багаторозрядні двійкові числа, порівнюють їх і, при збігу їх параметрів, роблять висновок про достовірність колективного електронного цифрового підпису, який відрізняється тим, що додатково генерують колективний відкритий ключ залежно від m відкритих ключів P![]() , P
, P![]() , ..., P
, ..., P![]() , де a1, a2, ..., am - натуральні числа, 2£m£n, aj£n і j = 1, 2, ..., m, причому принаймні одне з перевірних багаторозрядних двійкових чисел формують залежно від колективного відкритого ключа.
, де a1, a2, ..., am - натуральні числа, 2£m£n, aj£n і j = 1, 2, ..., m, причому принаймні одне з перевірних багаторозрядних двійкових чисел формують залежно від колективного відкритого ключа.
2. Спосіб за п. 1, який відрізняється тим, що відкриті ключі Р1, Р2, ..., Рn генерують у вигляді точок еліптичної кривої, для чого генерують еліптичну криву у вигляді сукупності точок, кожна з яких визначається парою багаторозрядних двійкових чисел, що є відповідно абсцисою і ординатою даної точки еліптичної кривої в декартовій системі координат, причому точки Р1, Р2, ..., Рn еліптичної кривої генерують за формулою Рi = kiG, де i = 1, 2, ..., n, G - додатково згенерована точка еліптичної кривої, що має порядок q, де q - просте багаторозрядне двійкове число, приймають m електронних документів, представлених багаторозрядними двійковими числами H1, Н2, ..., Нm, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел e і s, для чого генерують m випадкових багаторозрядних двійкових чисел t![]() , t
, t![]() , ..., t
, ..., t![]() , генерують m точок R
, генерують m точок R![]() , R
, R![]() , ..., R
, ..., R![]() еліптичної кривої за формулою
еліптичної кривої за формулою ![]() =
=![]() G, генерують точку R еліптичної кривої за формулою R =
G, генерують точку R еліптичної кривої за формулою R = 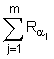 , після чого формують перше багаторозрядне двійкове число e колективного електронного цифрового підпису за формулою e = хR mod d, де xR - абсциса точки R і d - допоміжне просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел s
, після чого формують перше багаторозрядне двійкове число e колективного електронного цифрового підпису за формулою e = хR mod d, де xR - абсциса точки R і d - допоміжне просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел s![]() , s
, s![]() , ..., s
, ..., s![]() за формулою
за формулою ![]() = (
= (![]() - eH j
- eH j![]() ) mod q, після чого генерують друге багаторозрядне двійкове число s колективного електронного цифрового підпису за формулою
) mod q, після чого генерують друге багаторозрядне двійкове число s колективного електронного цифрового підпису за формулою 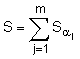 mod q, причому колективний відкритий ключ генерують у вигляді точки P еліптичної кривої, обчислюваної за формулою Р =
mod q, причому колективний відкритий ключ генерують у вигляді точки P еліптичної кривої, обчислюваної за формулою Р = 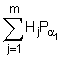 , і перше перевірне багаторозрядне двійкове число А формують за формулою А = xR’ mod d, де хR’ - абсциса точки R’ еліптичної кривої, обчисленої за формулою R’ = eP + sG, а друге перевірне багаторозрядне двійкове число В формують за формулою В = e.
, і перше перевірне багаторозрядне двійкове число А формують за формулою А = xR’ mod d, де хR’ - абсциса точки R’ еліптичної кривої, обчисленої за формулою R’ = eP + sG, а друге перевірне багаторозрядне двійкове число В формують за формулою В = e.
3. Спосіб за п. 1, який відрізняється тим, що відкриті ключі Р1, P2, ..., Pn генерують у вигляді точок еліптичної кривої, для чого генерують еліптичну криву у вигляді сукупності точок, кожна з яких визначається парою багаторозрядних двійкових чисел, що є відповідно абсцисою і ординатою даної точки еліптичної кривої в декартовій системі координат, причому точки Р1, Р2, ..., Рn еліптичної кривої генерують за формулою Рi = kiG, де i = 1, 2, ..., n, G - додатково згенерована точка еліптичної кривої, що має порядок q, де q - просте багаторозрядне двійкове число, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел e і s, для чого генерують m випадкових багаторозрядних двійкових чисел t![]() , t
, t![]() , ..., t
, ..., t![]() , генерують m точок R
, генерують m точок R![]() , R
, R![]() , ..., R
, ..., R![]() еліптичної кривої за формулою
еліптичної кривої за формулою ![]() =
=![]() G, генерують точку R еліптичної кривої за формулою
G, генерують точку R еліптичної кривої за формулою 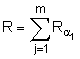 , після чого формують перше багаторозрядне двійкове число e колективного електронного цифрового підпису за формулою e = xRН mod d, де xR - абсциса точки R і S - допоміжне просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел
, після чого формують перше багаторозрядне двійкове число e колективного електронного цифрового підпису за формулою e = xRН mod d, де xR - абсциса точки R і S - допоміжне просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел ![]() ,
, ![]() , ...,
, ..., ![]() за формулою
за формулою ![]() = (
= (![]() - e
- e![]() ) mod q, після чого генерують друге багаторозрядне двійкове число s колективного електронного цифрового підпису за формулою
) mod q, після чого генерують друге багаторозрядне двійкове число s колективного електронного цифрового підпису за формулою 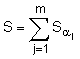 mod q, причому колективний відкритий ключ генерують у вигляді точки Р еліптичної кривої, обчислюваної за формулою
mod q, причому колективний відкритий ключ генерують у вигляді точки Р еліптичної кривої, обчислюваної за формулою 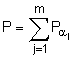 , і перше перевірне багаторозрядне двійкове число A формують за формулою A = xR’ mod d, де xR’ - абсциса точки R’ еліптичної кривої, обчисленої за формулою R’ = еР + sG, а друге перевірне багаторозрядне двійкове число В формують за формулою В = e.
, і перше перевірне багаторозрядне двійкове число A формують за формулою A = xR’ mod d, де xR’ - абсциса точки R’ еліптичної кривої, обчисленої за формулою R’ = еР + sG, а друге перевірне багаторозрядне двійкове число В формують за формулою В = e.
4. Спосіб за п. 1, який відрізняється тим, що відкриті ключі Р1, Р2, ..., Рn генерують у вигляді багаторозрядних двійкових чисел, для чого генерують просте багаторозрядне двійкове число p, таке, що p = Nz2 + 1, де N - парне натуральне багаторозрядне двійкове число і z - просте w-розрядне двійкове число, w > 64, причому багаторозрядні двійкові числа Р1, Р2, ..., Рn генерують за формулою Рi = kіz mod p, де i = 1, 2, ..., n, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел R і S, для чого генерують m випадкових багаторозрядних двійкових чисел ![]() ,
, ![]() , ...,
, ..., ![]() , генерують m допоміжних багаторозрядних двійкових чисел R
, генерують m допоміжних багаторозрядних двійкових чисел R![]() , R
, R![]() , ..., R
, ..., R![]() за формулою
за формулою ![]() =
= ![]() mod p, генерують перше багаторозрядне двійкове число R колективного електронного цифрового підпису за формулою
mod p, генерують перше багаторозрядне двійкове число R колективного електронного цифрового підпису за формулою 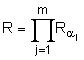 mod p, після чого формують допоміжне багаторозрядне двійкове число Е за формулою Е = RH mod d, де S - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S
mod p, після чого формують допоміжне багаторозрядне двійкове число Е за формулою Е = RH mod d, де S - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S![]() , S
, S![]() , ..., S
, ..., S![]() за формулою
за формулою ![]() =
= ![]()
![]() mod p, після чого генерують друге багаторозрядне двійкове число S колективного електронного цифрового підпису за формулою
mod p, після чого генерують друге багаторозрядне двійкове число S колективного електронного цифрового підпису за формулою 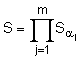 mod p, причому колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа Р, обчислюваного за формулою
mod p, причому колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа Р, обчислюваного за формулою 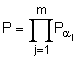 mod p, і перше перевірне багаторозрядне двійкове число А формують за формулою А = Sz mod p, а друге перевірне багаторозрядне двійкове число В формують за формулою В = РER mod p.
mod p, і перше перевірне багаторозрядне двійкове число А формують за формулою А = Sz mod p, а друге перевірне багаторозрядне двійкове число В формують за формулою В = РER mod p.
5. Спосіб за п. 1, який відрізняється тим, що відкриті ключі Р1, Р2, ..., Рn генерують у вигляді багаторозрядних двійкових чисел, для чого генерують просте багаторозрядне двійкове число p, таке, що p = Nz2 + 1, де N - парне натуральне багаторозрядне двійкове число і z - просте w-разрядное двійкове число, w > 64, причому багаторозрядні двійкові числа Р1, Р2, ..., Рn генерують за формулою Рi = k![]() mod p, де i = 1, 2, ..., n, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел Е і S, для чого генерують m випадкових багаторозрядних двійкових чисел t
mod p, де i = 1, 2, ..., n, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел Е і S, для чого генерують m випадкових багаторозрядних двійкових чисел t![]() , t
, t![]() , ..., t
, ..., t![]() , генерують m допоміжних багаторозрядних двійкових чисел R
, генерують m допоміжних багаторозрядних двійкових чисел R![]() , R
, R![]() , ..., R
, ..., R![]() за формулою
за формулою ![]() =
= ![]() mod p, генерують багаторозрядне двійкове число R за формулою
mod p, генерують багаторозрядне двійкове число R за формулою 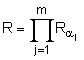 mod p, після чого формують перше багаторозрядне двійкове число Е колективного електронного цифрового підпису за формулою Е = RH mod d, де d - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S
mod p, після чого формують перше багаторозрядне двійкове число Е колективного електронного цифрового підпису за формулою Е = RH mod d, де d - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S![]() , S
, S![]() , ..., S
, ..., S![]() за формулою
за формулою ![]() =
= ![]() mod p, після чого генерують друге багаторозрядне двійкове число S колективного електронного цифрового підпису за формулою
mod p, після чого генерують друге багаторозрядне двійкове число S колективного електронного цифрового підпису за формулою 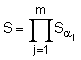 mod p, причому колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа Р, обчислюваного за формулою
mod p, причому колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа Р, обчислюваного за формулою 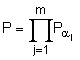 mod p, а перше А і друге В перевірні багаторозрядні двійкові числа формують, відповідно, за формулами А = (Sz P-Е mod p) H mod d і В = Е.
mod p, а перше А і друге В перевірні багаторозрядні двійкові числа формують, відповідно, за формулами А = (Sz P-Е mod p) H mod d і В = Е.
6. Спосіб за п. 1, який відрізняється тим, що відкриті ключі генерують у вигляді багаторозрядних двійкових чисел Р1, Р2, ..., Рn, для чого генерують просте багаторозрядне двійкове число р, причому багаторозрядні двійкові числа Р1, Р2, ..., Рn генерують за формулою Pi = ![]() mod p, де і = 1, 2, ..., n, g - додаткове згенероване багаторозрядне двійкове число, що має порядок q, де q - просте багаторозрядне двійкове число, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел Е і S, для чого генерують m випадкових багаторозрядних двійкових чисел t
mod p, де і = 1, 2, ..., n, g - додаткове згенероване багаторозрядне двійкове число, що має порядок q, де q - просте багаторозрядне двійкове число, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел Е і S, для чого генерують m випадкових багаторозрядних двійкових чисел t![]() , t
, t![]() , ..., t
, ..., t![]() , генерують m допоміжних багаторозрядних двійкових чисел R
, генерують m допоміжних багаторозрядних двійкових чисел R![]() , R
, R![]() , ..., R
, ..., R![]() за формулою
за формулою ![]() =
= ![]() mod p, генерують багаторозрядне двійкове число R за формулою
mod p, генерують багаторозрядне двійкове число R за формулою 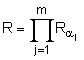 mod p, після чого формують перше багаторозрядне двійкове число Е колективного електронного цифрового підпису за формулою Е = RH mod d, де d - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S
mod p, після чого формують перше багаторозрядне двійкове число Е колективного електронного цифрового підпису за формулою Е = RH mod d, де d - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S![]() , S
, S![]() , ..., S
, ..., S![]() за формулою
за формулою ![]() = (
= (![]() ) mod q, після чого генерують друге багаторозрядне двійкове число S колективного електронного цифрового підпису за формулою
) mod q, після чого генерують друге багаторозрядне двійкове число S колективного електронного цифрового підпису за формулою 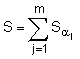 mod q, причому колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа Р, обчислюваного за формулою
mod q, причому колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа Р, обчислюваного за формулою 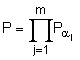 mod p, і перше перевірне багаторозрядне двійкове число А формують за формулою А = R’H mod d, де R’ - багаторозрядне двійкове число, обчислене за формулою R’ = Р-Egs mod p, а друге перевірне багаторозрядне двійкове число B формують за формулою В = Е.
mod p, і перше перевірне багаторозрядне двійкове число А формують за формулою А = R’H mod d, де R’ - багаторозрядне двійкове число, обчислене за формулою R’ = Р-Egs mod p, а друге перевірне багаторозрядне двійкове число B формують за формулою В = Е.
7. Спосіб за п. 1, який відрізняється тим, що відкриті ключі Р1, Р2, …, Рn генерують у вигляді багаторозрядних двійкових чисел, для чого генерують просте багаторозрядне двійкове число p, причому багаторозрядні двійкові числа Р1, Р2, ..., Рn генерують за формулою Рi = ![]() mod р, де i = 1, 2, ..., n, g - додаткове згенероване багаторозрядне двійкове число, що має порядок q, де q - просте багаторозрядне двійкове число, приймають m електронних документів, представлених багаторозрядними двійковими числами Н1, Н2, ..., Нm, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел Е і S, для чого генерують m випадкових багаторозрядних двійкових чисел t
mod р, де i = 1, 2, ..., n, g - додаткове згенероване багаторозрядне двійкове число, що має порядок q, де q - просте багаторозрядне двійкове число, приймають m електронних документів, представлених багаторозрядними двійковими числами Н1, Н2, ..., Нm, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел Е і S, для чого генерують m випадкових багаторозрядних двійкових чисел t![]() , t
, t![]() , ..., t
, ..., t![]() , генерують m допоміжних багаторозрядних двійкових чисел R
, генерують m допоміжних багаторозрядних двійкових чисел R![]() , R
, R![]() , ..., R
, ..., R![]() за формулою
за формулою ![]() =
= ![]() mod p, генерують багаторозpядне двійкове число R за формулою
mod p, генерують багаторозpядне двійкове число R за формулою 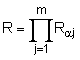 mod p, після чого формують перше багаторозрядне двійкове число Е колективного електронного цифрового підпису за формулою Е = R mod d, де d - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S
mod p, після чого формують перше багаторозрядне двійкове число Е колективного електронного цифрового підпису за формулою Е = R mod d, де d - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S![]() , S
, S![]() , ..., S
, ..., S![]() за формулою
за формулою ![]() mod q, після чого генерують друге багаторозрядне двійкове число S колективного електронного цифрового підпису за формулою
mod q, після чого генерують друге багаторозрядне двійкове число S колективного електронного цифрового підпису за формулою 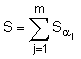 mod q, причому колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа P, обчислюваного за формулою
mod q, причому колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа P, обчислюваного за формулою 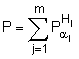 mod р, і перше перевірне багаторозрядне двійкове число А формують за формулою А = R’ mod d, де R’ - багаторозрядне двійкове число, обчислене за формулою R = Р-E gs mod p, а друге перевірне багаторозрядне двійкове число В формують за формулою В = Е.
mod р, і перше перевірне багаторозрядне двійкове число А формують за формулою А = R’ mod d, де R’ - багаторозрядне двійкове число, обчислене за формулою R = Р-E gs mod p, а друге перевірне багаторозрядне двійкове число В формують за формулою В = Е.
Текст
1. Спосіб формування і перевірки достовірності колективного електронного цифрового підпису для засвідчення електронного документа, який полягає в тому, що генерують сукупність з n > 2 секретних ключів у вигляді багаторозрядних двійкових чисел k1 , k2 , ..., kn, по секретних ключах формують n відкритих ключів Р 1, Р2, ..., Рn, відповідно, приймають принаймні один електронний документ, представлений багаторозрядним двійковим числом H, залежно від прийнятого електронного документа і від значення принаймні одного секретного ключа формують колективний електронний цифровий підпис Q у вигляді двох або більше багаторозрядних двійкових чисел, формують перше А і друге В перевірні багаторозрядні двійкові числа, порівнюють їх і, при збігу їх параметрів, роблять висновок про достовірність колективного електронного цифрового підпису, який відрізняється тим, що додатково генерують колективний відкритий ключ залежно від m відкритих ключів P a1 , P a 2 , ..., P am , де a 1, a 2, ..., 2 3 31105 3. Спосіб за п. 1, який відрізняється тим, що відкриті ключі Р1, P2, ..., Pn генерують у вигляді точок еліптичної кривої, для чого генерують еліптичну криву у вигляді сукупності точок, кожна з яких визначається парою багаторозрядних двійкових чисел, що є відповідно абсцисою і ординатою даної точки еліптичної кривої в декартовій системі координат, причому точки Р1, Р2, ..., Рn еліптичної кривої генерують за формулою Р i = kiG, де i = 1, 2, ..., n, G - додатково згенерована точка еліптичної кривої, що має порядок q, де q - просте багаторозрядне двійкове число, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел e і s, для чого генерують m випадкових багаторозрядних двійкових чисел t a1 , t a 2 , ..., t am , генерують m точок R a1 , R a 2 , ..., R am еліптичної кривої за формулою Ra j = t a j G, генерують точку R еліптичної кривої за формулою 4 перше багаторозрядне двійкове число R колективного електронного цифрового підпису за m åR aj mod p, після чого формують допоміжне багаторозрядне двійкове число Е за формулою Е = RH mod d, де S додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S a1 , S a 2 , ..., S am за формулою Sa j = kE ta j a mod j p, після чого генерують друге багаторозрядне двійкове число S колективного електронного цифрового підпису за формулою m ÕS S= aj mod p, причому колективний відкритий j= 1 ключ генерують у вигляді багаторозрядного двійкового числа Р, обчислюваного за формулою m aj , після чого формують перше P= j= 1 mod q, після чого генерують друге багаторозрядне двійкове число s колективного електронного m цифрового підпису за формулою S = åS aj mod j= 1 q, причому колективний відкритий ключ генерують у вигляді точки Р еліптичної кривої, обчислюваної m за формулою P= åP aj , і перше перевірне j= 1 багаторозрядне двійкове число A формують за формулою A = xR’ mod d, де xR’ - абсциса точки R’ еліптичної кривої, обчисленої за формулою R’ = еР + sG, а друге перевірне багаторозрядне двійкове число В формують за формулою В = e. 4. Спосіб за п. 1, який відрізняється тим, що відкриті ключі Р1, Р2, ..., Рn генерують у вигляді багаторозрядних двійкових чисел, для чого генерують просте багаторозрядне двійкове число p, таке, що p = Nz2 + 1, де N - парне натуральне багаторозрядне двійкове число і z - просте wрозрядне двійкове число, w > 64, причому багаторозрядні двійкові числа Р1, Р2, ..., Рn генерують за формулою Рi = kіz mod p, де i = 1, 2, ..., n, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел R і S, для чого генерують m випадкових багаторозрядних двійкових чисел t a 1 , ..., ÕP aj mod p, і перше перевірне j= 1 багаторозрядне двійкове число e колективного електронного цифрового підпису за формулою e = xRН mod d, де xR - абсциса точки R і S - допоміжне просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел sa 1 , sa 2 , ..., s a m за формулою sa j = ( t a 1 - e k a1 ) ta2 , ÕR j= 1 m R= R= формулою tam , генерують m допоміжних багаторозрядних двійкових чисел R a1 , R a 2 , ..., R am за формулою Ra j = t z aj mod p, генерують багаторозрядне двійкове число А формують за формулою А = Sz mod p, а друге перевірне багаторозрядне двійкове число В формують за формулою В = РER mod p. 5. Спосіб за п. 1, який відрізняється тим, що відкриті ключі Р1, Р2, ..., Рn генерують у вигляді багаторозрядних двійкових чисел, для чого генерують просте багаторозрядне двійкове число p, таке, що p = Nz2 + 1, де N - парне натуральне багаторозрядне двійкове число і z - просте wразрядное двійкове число, w > 64, причому багаторозрядні двійкові числа Р1, Р2, ..., Рn генерують за формулою Р i = k iz mod p, де i = 1, 2, ..., n, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел Е і S, для чого генерують m випадкових багаторозрядних двійкових чисел t a1 , t a2 , ..., t am , генерують m допоміжних багаторозрядних двійкових чисел R a1 , R a 2 , ..., R am за формулою Ra j = t z mod p, генерують aj багаторозрядне двійкове число R за формулою m R= ÕR aj mod p, після чого формують перше j= 1 багаторозрядне двійкове число Е колективного електронного цифрового підпису за формулою Е = RH mod d, де d - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S a1 , S a 2 , ..., S am за формулою S a j = k E t a j mod p, після чого aj генерують друге багаторозрядне двійкове число S колективного електронного цифрового підпису за m формулою S= ÕS j= 1 aj mod p, причому 5 31105 колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа Р, m обчислюваного за формулою P = ÕP aj mod p, а j =1 перше А і друге В перевірні багаторозрядні двійкові числа формують, відповідно, за формулами А = (Sz P-Е mod p) H mod d і В = Е. 6. Спосіб за п. 1, який відрізняється тим, що відкриті ключі генерують у вигляді багаторозрядних двійкових чисел Р1, Р2, ..., Рn, для чого генерують просте багаторозрядне двійкове число р, причому багаторозрядні двійкові числа Р1, Р2, ..., Рn генерують за формулою P i = gk i mod p, де і = 1, 2, ..., n, g - додаткове згенероване багаторозрядне двійкове число, що має порядок q, де q - просте багаторозрядне двійкове число, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел Е і S, для чого генерують m випадкових багаторозрядних двійкових чисел t a1 , t a2 , ..., t am , генерують m допоміжних багаторозрядних двійкових чисел R a1 , R a 2 , ..., R am за формулою Ra j = g ta j mod p, генерують багаторозрядне двійкове число R за формулою m R= ÕR aj mod p, після чого формують перше j= 1 багаторозрядне двійкове число Е колективного електронного цифрового підпису за формулою Е = RH mod d, де d - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S a1 , S a 2 , ..., S am за формулою S a j = ( t a j + Eka j ) mod q, після чого генерують друге багаторозрядне двійкове число S колективного електронного цифрового m підпису за формулою S = åS aj mod q, причому j= 1 колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа Р, m обчислюваного за формулою P = ÕP aj mod p, і j=1 перше перевірне багаторозрядне двійкове число А формують за формулою А = R’H mod d, де R’ багаторозрядне двійкове число, обчислене за формулою R’ = Р-Egs mod p, а друге перевірне Корисна модель відноситься до області електрозв’язку і обчислювальної техніки, а конкретніше до області криптографічних способів аутентифікації електронних повідомлень, що передаються по телекомунікаційних мережах і мережах ЕОМ і може бути використана в системах 6 багаторозрядне двійкове число B формують за формулою В = Е. 7. Спосіб за п. 1, який відрізняється тим, що відкриті ключі Р1, Р2, …, Рn генерують у вигляді багаторозрядних двійкових чисел, для чого генерують просте багаторозрядне двійкове число p, причому багаторозрядні двійкові числа Р1, Р2, ..., Рn генерують за формулою Рi = gk i mod р, де i = 1, 2, ..., n, g - додаткове згенероване багаторозрядне двійкове число, що має порядок q, де q - просте багаторозрядне двійкове число, приймають m електронних документів, представлених багаторозрядними двійковими числами Н1, Н2, ..., Нm, а колективний електронний цифровий підпис формують у вигляді пари багаторозрядних двійкових чисел Е і S, для чого генерують m випадкових багаторозрядних двійкових чисел t a1 , t a2 , ..., t am , генерують m допоміжних багаторозрядних двійкових чисел R a1 , R a 2 , ..., R am за формулою Ra j = g ta j mod p, генерують багаторозpядне двійкове число R за формулою m R= ÕR aj mod p, після чого формують перше j= 1 багаторозрядне двійкове число Е колективного електронного цифрового підпису за формулою Е = R mod d, де d - додаткове просте багаторозрядне двійкове число, потім генерують m багаторозрядних двійкових чисел S a1 , S a 2 , ..., S am за формулою S a j = ( t a j + EHj k a j ) mod q, після чого генерують друге багаторозрядне двійкове число S колективного електронного m цифрового підпису за формулою S = åS aj mod j= 1 q, причому колективний відкритий ключ генерують у вигляді багаторозрядного двійкового числа P, m обчислюваного за формулою P = åP j= 1 Hj aj mod р, і перше перевірне багаторозрядне двійкове число А формують за формулою А = R’ mod d, де R’ багаторозрядне двійкове число, обчислене за формулою R = Р-E gs mod p, а друге перевірне багаторозрядне двійкове число В формують за формулою В = Е. передачі електронних повідомлень (документів), засвідчених колективним електронним цифровим підписом (ЕЦП), представленим у вигляді багаторозрядного двійкового числа (БДЧ). Тут і далі під БДЧ розуміється електромагнітний сигнал в двійковій цифровій формі, параметрами якого є: 7 число бітів і порядок проходження їх одиничних і нульових значень. Відомий спосіб формування і перевірки ЕЦП [1, стор.133-134], [2, стор.43], якій полягає в такій послідовності дій: формують секретний ключ у вигляді трьох простих БДЧ р, q і d, формують відкритий ключ (n, e) у вигляді пари БДЧ n і e, де n - число, що є добутком двох простих БДЧ р і q, і є - БДЧ, задовольняюче умові ed = 1 mod (p-1)(q-1), приймають електронний документ (ЕД), представлений БДЧ H; залежно від значення Н і значення секретного ключа формують ЕЦП у вигляді БДЧ Q = S - Нd mod n; формують перше перевірочне БДЧ А = H; формують друге перевірочне БДЧ В, для чого БДЧ S підносять до цілочисельнсго ступеня e по модулю n: В = Se mod n; порівнюють сформовані перевірочні БДЧ А і В; при збігу параметрів порівнюваних БДЧ А і В роблять висновок про достовірність ЕЦП. Недоліком відомого способу є відносно великий розмір підпису і необхідність збільшення розміру підпису при розробці нових більш ефективних методів розкладання числа п на множники або при зростанні продуктивності сучасних обчислювальних пристроїв. Це пояснюється тим, що значення елементу підпису S обчислюються шляхом виконання арифметичних операцій по модулю n, а стійкість ЕЦП визначається складністю розкладання модуля n на множники р і q. Відомий також спосіб формування і перевірки достовірності ЕЦП Ель-Гамаля [3, стор.156-159], який включає такі дії: формують просте БДЧ р і двійкове число G, що є первісним корінням по модулю р, генерують секретний ключ у вигляді БДЧ х, залежно від секретного ключа формують відкритий ключ у вигляді БДЧ Y = Gx mod p, приймають ЕД, представлений у вигляді БДЧ Н, залежно від Н і секретного ключа формують ЕЦП Q у вигляді двох БДЧ S і R, тобто Q = (S, R); здійснюють процедуру перевірки достовірності ЕЦП, що включає обчислення двох контрольних параметрів з використанням початкових БДЧ р, G, Y, Н і S шляхом зведення БДЧ G, Y, R в дискретний ступінь по модулю р і порівняння обчислених контрольних параметрів; при збігу значень контрольних параметрів роблять висновок про достовірність ЕЦП. Недоліком даного способу також є відносно великий розмір ЕЦП. Це пояснюється тим, що значення елементів підпису S і R обчислюють шляхом виконання арифметичних операцій по модулю p - 1 і по модулю p, відповідно. Відомий також спосіб формування і перевірки ЕЦП Шнорра [4, cтор.53], якій полягає в такій послідовності дій: формують просте БДЧ р, таке що р = Nq + 1, де q - просте БДЧ; формують просте БДЧ а, таке що а ¹ 1 і aq mod p = 1; 31105 8 методом генерації випадкової рівноімовірної послідовності формують секретний ключ у вигляді БДЧ х; формують відкритий ключ у вигляді БДЧ у по формулі у = ax mod p; приймають ЕД, представлений БДЧ М; формують ЕЦП у вигляді пари БДЧ (e, s), для чого генерують випадкове БДЧ t, формують БДЧ R по формулі R = at mod p, формують БДЧ e = f(M\\R), де знак || позначає операцію приєднання двох БДЧ і f - деяка специфікована хэш-функція, значення якої має фіксовану довжину (звичні 160 або 256 біт), незалежний від розміру аргументу, тобто від розміру БДЧ М||R, а потім, формують БДЧ s по формулі s = (t-ex) mod q; формують перше перевірочне БДЧ А, для чого генерують БДЧ R’ по формулі R’ - asyemod p і формують БДЧ e’ = f(M||R’); формують друге перевірочне БДЧ В шляхом копіювання БДЧ e: В = e; порівнюють сформовані перевірочні БДЧ А і В; при збігу параметрів порівнюваних БДЧ А і В роблять висновок про достовірність ЕЦП. Недоліком способу є відносно висока обчислювальна складність процедури формування і перевірки ЕЦП, що пов’язано з тим, що для забезпечення мінімально необхідного рівня стійкості вимагається використовувати простий модуль p розрядністю не менше 1024 біт. Відомий також спосіб формування і перевірки ЕЦП ГОСТ Р 34.10-2001 15, стор.110-111, 6], прийнятий за прототип, згідно якому ЕЦП формується у вигляді пари БДЧ r і s, для чого генерують еліптичну криву (ЕК) у вигляді сукупності точок, причому кожна точка представляється двома координатами в декартовій системі координат у вигляді двох БДЧ, званих абсцисою (х) і ординатою (у), потім здійснюють операції генерації точок ЕК, складання точок ЕК і множення точки ЕК на число, а також арифметичні операції над БДЧ, після чого в результаті виконаних операцій формуються БДЧ r i s. Вказані операції над точками виконуються як операції над БДЧ, є координатами точок, по відомих формулах [5, стор.110-111]. Операція складання двох точок А і В з координатами (хА, уА) і (xВ, yВ), відповідно, виконується по формулах: хс = k2 – хA – хB mod р і ус = k (хA - хB) – уA mod p, yB - y A x - xA де k = B mod p, якщо точки А і В не рівні, 3 xA + a 2y A mod p, якщо точки А і В рівні. і k = Операція множення точки А на натуральне число n визначається як багатократне складання точки А: nА = A + А + ... + А (n раз). Результатом множення будь-якої точки ЕК на нуль визначається точка О, що є нескінченно віддаленою точкою. Дві точки А = (х, у) і -А = (х-у) називаються протилежними. Множення на ціле негативне число -n визначається таким чином: (n)А = n(-А). За означенням приймають, що сума двох протилежних точок рівна нескінченно віддаленій точці О. 9 У прототипі генерують ЕК, що описана рівнянням y2 = х3 + ах + b mod р. Тобто генерують числа a, b і р, яки є параметрами ЕК і однозначно задають множину точок ЕК, абсциса і ордината кожної з яких задовольняє, вказаному рівнянню. Спосіб працює таким чином: генерують еліптичну криву (ЕК), яка є сукупністю пар БДЧ, званих точками ЕК? що володіють певними властивостями; методом генерації випадкової рівноімовірної послідовності формують секретні ключі у вигляді БДЧ k1, k2, ..., kn; формують відкриті ключі у вигляді точок ЕК Р1, Р2, ..., Рn, для чого генерують точку G, що має простий порядок q (порядком точки ЕК називається якнайменше позитивне ціле число q, таке що результатом множення даної точки на число q є так звана нескінченно віддалена точка О; результатом множення будь-якої точки ЕК на нуль за означенням є точка О [5, стор.98-105]), i обчислюють відкриті ключі шляхом множення точки G на БДЧ k1, k2, ..., kn, тобто формують відкриті ключі по формулах P1 = k1G, P2 = k2G, ,..., Pn = knG; приймають ЕД, представлений БДЧ Н; генерують випадкове БДЧ 0 < t < q, по якому формують точку R по формулі R = tG; формують ЕЦП Q у вигляді пари БДЧ (r, s), для чого генерують БДЧ r по формулі r = xR mod q, де xR - абсциса точки R, а потім генерують БДЧ s по формулі s = (tH + rk1 ) mod q, де 1 < i 2 секретних ключів у вигляді багаторозрядних двійкових чисел k1, k2 , ..., kn, по секретних ключах формують п відкритих ключів Р1, P2, ..., Рn, 31105 10 відповідно, приймають, принаймні, один електронний документ, представлений багаторозрядним двійковим числом Н, залежно від прийнятого електронного документа і від значення, принаймні, одного секретного ключа формують колективний електронний цифровий підпис Q у вигляді двох або більш багаторозрядних двійкових чисел, формують перше А і друге B перевірочні багаторозрядні двійкові числа, порівнюють їх і при збігу їх параметрів роблять висновок про достовірність колективного електронного цифрового підпису, причому додатково генерують колективний відкритий ключ залежно від m відкритих ключів P a1 , P a 2 , ..., P am , де a 1, a 2, ..., am - натуральні числа, 2 2. Користувачі умовно позначаються номерами i = 1, 2, ..., n. Цей номер використовується як індекс, вказуючий на те, якому користувачу належить секретний і відкритий ключі, або на те, який з користувачів генерує відзначені індексом БДЧ або точки ЕК. З сукупності n користувачів деяка їх 15 31105 підмножина, що складається з m довільно вибраних користувачів, може бути задана номерами користувачів, що входять в дану підмножину, наприклад номерами a 1, a 2, ..., a m, кожний з яких вибирається з множиш чисел 1, 2, ..., n. Таким чином, числа a j, де j = 1, 2, ..., m, є вибіркою довільних m номерів з множини {1, 2 ., n), при цьому m < n.Відповідно цьому сукупність відкритих ключів, наприклад, точок P a 1 , P a 2 , ..., P am ЕК є вибіркою з множини всіх відкритих ключів Р1, Р2, ..., Рn, а сукупність секретних ключів k a 1 , k a 2 , ..., k a m є вибіркою з множини всіх секретних ключів к1 , к2, ..., кn, де i = 1, 2, ..., n. Коректність заявленого способу доводиться теоретично. Розглянемо, наприклад, варіант реалізації способу по п. 3 формули корисної моделі. Колективний відкритий ключ, відповідний підмножині користувачів з умовними номерами a 1, a 2, ..., a m , є точкою æm P = Pa 1 + Pa 2 + ... + Pa m = k a 1 G + k a 2 G + ... + k a m G = ç å k a j ç j =1 è . Значення sa j , які є «частками» користувачів в колективному підпису, генеруються по формулі s aj = (t aj - еk aj ) mod q, тому, m m m m m j =1 j =1 j =1 j =1 j =1 å s a j º å t a j - å ek a j º å t a j - e å k a j modq . Значення точки R’, що використовується для формування першого перевірочного БДЧ А, генерується по формулі R’ = eР + sG, тобто воно рівне m m m æm ö æm ö æ m ö æm ö ç ÷ ç ÷ ç ÷ ç ÷ R' = eP + sG = eç å k a j ÷G + ç å t a j - e å k a j ÷G = ç e å k a j + å t a j - e å k a j ÷G = ç å t a j ÷ G = R j=1 j= 1 j=1 è j= 1 ø è j= 1 ø è j= 1 ø è j= 1 ø . Отже, А = хR’H mod d = xRH mod d = e = B, т. е. правильно сформований колективний підпис задовольняє процедурі перевірки підпису, т. e. коректність процедур генерації і перевірки ЕЦП доведена. Розглянемо приклади реалізації заявленого технічного рішення з використовуванням ЕК, описуваної рівнянням у2 = х3 + ах + b mod p, де конкретні значення використаних параметрів описані в чисельних прикладах, то наводяться нижче. Використані в прикладах ЕК були згенерувані за допомогою програми, розробленої спеціально для генерації ЕК, генерації точок ЕК, включаючи точки із заданим порядком, і виконання операцій над точками ЕК. Ті БДЧ, що приводяться в прикладі, записані скорочено у вигляді десяткових чисел, які в обчислювальних пристроях представляються і перетворяться в двійковому вигляді, тобто у вигляді послідовності сигналів високого і низького потенціалу. Даний приклад ілюструє спосіб по п.1 відповідно до варіанту реалізації по п. 2 формули корисної моделі. В ньому використовується ЕК з параметрами, що забезпечують достатню стійкість ö ÷G ÷ ø 16 для вживання при рішенні реальних практичних задач аутентифікації інформації. Цей приклад ілюструє реальні розміри чисел, які використовуються на практиці при генерації і перевірці достовірності колективного ЕЦП. Особливістю даного прикладу є те, що приймають три різних ЕД, представлених БДЧ Н1, Н2, Н3. При цьому перший користувач підписує перший ЕД, другий користувач - другий ЕД і третій користувач третій ЕД. Можливість реалізації колективного ЕЦП з такими властивостями забезпечується за рахунок того, що при перевірці ЕЦП використовується колективний відкритий ключ, формований залежно від відкритих ключів користувачів по формулі Р = Н1Р1 + Н2Р2 + Н3Р3. У прикладі використовується ЕК, визначувана такими параметрами: а = 5521767865737634555390416300599776622347333 359784, b = 9717196 і p = 5521767865737634555390416300599776622347333 359787. Дана ЕК містить кількість точок, рівну простому числу V= 5521767865737634555390416228783886913339823 841723, тобто будь-яка її точка має порядок q, рівний значенню V: q = V. Розглянемо колектив з трьох користувачів. При формуванні і перевірці достовірності колективного ЕЦП (підписом є пара чисел e і s.) виконують таку послідовність дій. 1. Генерують ЕК з параметрами вказаними вище. 2. Формують секретні ключі у вигляді випадкових БДЧ k1, k2 і k3 : k1 = 8182108890892890101467333434019 ключ першого користувача; k2 = 3952504539403758278808581024791 ключ другого користувача; k3 = 9763160941600092631935520658071 ключ третього користувача. 3. Формують відкриті ключі у вигляді точок ЕК Р1, Р2, Р3, для чого 3.1. Генерують точку G, що має порядок q: G=(405813899881769956997667835823333595 8495037969465, 7685639263360368257184952189163086824941161 44160); 3.2. Генерують точки Р1, Р2, Р3, по формулі Р1 = kjG, де i = 1, 2, 3: Р1 = (240676766592815889944690616582174721888357 4602371, 562377648521692290689031507205008060205 345636991); Р2=(348708108378027085357389414044825237 922683510732, 1402026191996080196399482770468472598076052 599809) Р3 = (430716607783351930106332253302416200509102 5020313, 528029631254915602814890591421557065551 4986217509). 17 4. Приймають три ЕД, представлених БДЧ Н1, H2 і Н3. H1 = 1557080922155979101683141547519172206337121 78686; Н2 = 3812498990028819155316571350634376652814331 770527; Н3 = 8925999026871145131520337612117778680659192 576033. 5. Формують ЕЦП Q у вигляді двох БДЧ e і s, для чого виконують таки дії. 5.1, Перший, другий і третій користувачі генерують випадкові БДЧ t1, t2 і t3, відповідне: t1 = 2090880922625982683584460167862382379; t2 = 5360383526856663700583896205266418341; t3 = 7671118810723142352012317453400887449. 5.2. Потім перший, другий і третій користувачі генерують точки R1, R2 і R3, відповідно по формулі Ri = riG: R1 (453336007529244660885066440036471159220513 6618460, 175061337062232179584348686477324762101 164050095); R2 =(19582792238279020473793364652858954353301 40185477, 883050890825623295514423424297049431856 4852573); R3 =(50386160288529598775095540817896674368537 94753557, 209613157933044677924551688484534713038 841468913). 5.3. Генерують точку R по формулі R = R1 + R2+ R3: R =(25970979702636108635460694368339945800021 05418569, 3304915040 104400813802374282473985550015521973383). 5.4. Формують БДЧ e по формулі e = хR mod d, де xR - абсциса точки R і d-допоміжне просте БДЧ (d = 7118198218659321028989011): e = 5079008233076932087473789. 5.5. Перший, другий і третій користувачі генерують БДЧ s1, s2 і s3, відповідно, по формулі si = (ti – eHiki) mod q, де q = N і i = 1, 2, 3: s1 = 1334449638753333889237431872714731229154432 05289; s2 = 1S8766165320384794471028245083561255162008 1427016; s3 =48506961619559911255593180845550213355803 02189827. 5.6. Генерують БДЧ s = s1 + s 2 + s 3 mod q: 31105 18 s = 1350034913297537903802927493878220096776002 980409. 6. Формують перше перевірочне БДЧ А, для чого виконують таку послідовність дій. 6.1 Формують колективний відкритий ключ у вигляді точки Р по формулі Р = H1Р1 +H2Р2 + H3Р3: H1P1 = (138608434900254542451166892694557506683840 7867380, 454363373195884010112484581877184100437 4561021017) Н2P2 = (299211431532419026428141393395396288778694 972469, 530032709442115487602206494687620629685 3312043729) H3Р3 = (452352848795452290087869487789555696379634 5154180, 410082610348097279898099690919652619932 7733122181) Р =(22842653948590033809093887809046461154863 8254406, 120227817455309523113538906020964990253 5727110543). 6.2 Генерують точку R’= eP + sG: eP = (455684817959588714140072672389132143860230 7875189, 288377928957475698317738795561807371973 1329543379); sG = (136035281553157716668491223313400149638981 6081366, 354326978724723578190089740410427934164 4752005600); R’ = (2597GC)79702636108635460694368339945800021 05418569, 330491504010440081380237428247398555001 5521973383); 6.3 Генерують БДЧ А по формулі А = хR’ mod d, де допоміжні БДЧ d = 7118198218659321028989011: А = 5079008233076932087473789. 7. Формують друге перевірочне БДЧ В шляхом копіювання БДЧ e: В = e = 5079008233076932087473789. 8. Порівнюють перше А і друге В перевірочні БДЧ. Порівняння показує, що параметри БДЧ А і В співпадають. Збіг значень А і В означає, що колективний ЕЦП є справжним, тобто відноситься до прийнятих ЕД, представлених БДЧ Н1, Н2 і Н3, причому перший користувач підписав ЕД. представлений БДЧ Н1, другий користувач -ЕД, представлений БДЧ Н2, а третій користувач –ЕД, представлений БДЧ Н3. Даний приклад ілюструє спосіб по п. 1 відповідно до варіанту реалізації по п. 3 формули корисної моделі. 19 У даному прикладі використовується ЕК, секретні і відкриті ключі користувачів такі ж як і в попередньому прикладі. В прикладі використовується ЕК. визначувана такими параметрами: а = 5521767865737634555390416300599776622347333 359784, b = 9717196 і р = 5521767865737634555390416300599776622347333 359787. Дана ЕК містить кількість точок, рівну простому числу V= 5521767865737634555390416228783886913339823 841723, тобто будь-яка її точка має порядок q, рівний значенню V: q = V. Розглянемо колектив з трьох користувачів. При формуванні і перевірці достовірності колективного ЕЦП (підписом є пара БДЧ е і s) виконують таку послідовність дій. 1. Генерують ЕК з параметрами вказаними вище. 2. Формують секретні ключі у вигляді випадкових БДЧ: k1 = 8182108890892890101467333434019 ключ першого користувача; k2 = 3952504539403758278808581024791 ключ другого користувача; k3 = 9763160941600092631935520658071 ключ третього користувача. 3. Формують відкриті ключі у вигляді точок ЕК Р1, Р2, Р3, для чого 3.1. Генерують точку G, що має порядок q: G = (405813899881769956997667835823333595849503 7969465, 768563926336036825718495218916308682494 116144160); 3.2. Генерують точки Р1, Р2, Р3, по формулі Р1 = kjG, де i = 1, 2, 3: Р1 = (240676766592815889944690616582174721888357 4602371, 562377648521692290689031507205008060205 345636991); Р2 = (348708108378027085357389414044825237922683 510732, 140202619199608019639948277046847259807 6052599809) Р3 = (430716607783351930106332253302416200509102 5020313, 528029631254915602814890591421557065551 4986217509). 4. Приймають ЕД, представлений, наприклад, наступним БДЧ Н (як Н може бути узята, зокрема, хєш-функція від ЕД): H = 8925999026871145131520337612117778606591925 76033. 5. Формують ЕЦП Q у вигляді двох БДЧ e і s, для чого виконують таки дії. 5.1, Перший, другий і третій користувачі генерують випадкові БДЧ t1, t2 і t3, відповідне: 31105 20 t1 = 2090880922625982683584460167862382379; t2 = 5360383526856663700583896205266418341; t3 = 7671118810723142352012317453400887449. 5.2. Потім перший, другий і третій користувачі генерують точки R1, R2 і R3, відповідно по формулі Ri = riG: R1 = (453336007529244660885066440036471159220513 6618460, 117506133706223217958434868647732476210 1164050095); R2 = (195827922382790204737933646528589543533014 0185477, 883050890825623295514423424297049431856 4852573); R3 =(50386160288529598775095540817896674368537 94753557, 209613157933044677924551688484534713038 841468913). 5.3. Генерують точку R по формулі R = R1 + R2+ R3: R = (259709797026361086354606943683399458000210 5418569, 3304915040 104400813802374282473985550015521973383). 5.4. Формують БДЧ e по формулі e = хR mod d, де xR - абсциса точки R і d - допоміжне просте БДЧ (d = 7118198218659321028989011): e = 5079008233076932087473789. 5.5. Перший, другий і третій користувачі генерують БДЧ s1, s2 і s3, відповідно, по формулі si = (ti – eHiki) mod q, де q = N і i = 1, 2, 3: s1 = 3598499834242743077162548779849531591492835 98626; s2 = 2228471503399271451844174588034195792013686 207551; s3 = 3321295738385055881020248326363803564813773 402448. 5.6. Генерують друге БДЧ s колективного електронного цифрового підпису по формулі s = s1 + s 2 + s 3 mod q: s = 3878493594709670851901261563599065602636919 366902. 6. Формують перше перевірочне БДЧ А, для чого виконують таку послідовність дій. 6.1 Формують колективний відкритий ключ у вигляді точки Р по формулі Р = Р1 + Р2 + Р3: P = (259709797026361086356069436833994880002105 48569, 330491504010440081380237428247398555001 5521973383). 6.2 Генерують точку R’= eP + sG: 21 eP = (146955471348564375364922408624400975297984 578370, 506748749888997175271628334751609221739 7817107870); sG = (292535746865117796446681364223363153817497 1712513, 599550386022153150210626227063281723596 625174740); R’ = (259709797026361086354606943683399458000210 5418569, 330491504010440081380237428247398555001 5521973383); 6.3 Генерують БДЧ А по формулі А = хR’ mod d, де допоміжні БДЧ d = 7118198218659321028989011: А = 4927124871592959793329711. 7. Формують друге перевірочне БДЧ В шляхом копіювання БДЧ e: В = e = 5079008233076932087473789. 8. Порівнюють перше А і друге В перевірочні БДЧ. Порівняння показує, що параметри БДЧ А і В співпадають. Збіг значень А і В означає, що колективний ЕЦП є справжним, тобто відноситься до прийнятого ЕД, представленому БДЧ Н, і сформований трьома користувачами, по відкритих ключах, по яких був сформований колективний відкритий ключ, використаний для перевірки достовірності підпису. Даний приклад ілюструє спосіб по п. 1 відповідно до варіанту реалізації по п. 4 формули корисної моделі. Цей приклад представляє варіант реалізації способу, що заявляється, з використанням обчислень по простому модулю. Ті БДЧ, що приводяться в прикладі, записані скорочено у вигляді десяткових чисел, які в обчислювальних пристроях представляються і перетворяться в двійковому вигляді, тобто у вигляді послідовності сигналів високого і низького потенціалу. При формуванні і перевірці достовірності колективного ЕЦП, сформованого двома користувачами (підписом є пара чисел R і S.), виконують таку послідовність дій. 1 Формують просте число, таке ще р - 1 містить квадрат великого простого числа z, тобто р = Nz2 + 1, де N - парне число: р = 4153476369892465269012870897623282390047400 100719, де z = 132104433635297779312031; N = 238. 2. Формують секретний ключ у вигляді випадкового БДЧ k1 =3526378981324543353612; k2 = 1134645756882454332351. 3. Формують відкриті ключі першого і другого користувачів у вигляді БДЧ Р1 і Р2, відповідно, по формулі Р1 = kiz mod p: Р1 = 3864858100219352940369774847788552018367055 197706; 31105 22 Р2 = 1007524924840372827951240203079659934380448 88870. 4. Приймають ЕД, представлений, наприклад, БДЧ H (як Н може бути узята, зокрема, хєшфункція від ЕД): Н = 73568790119017231823457. 5. Формують ЕЦП у вигляді пари чисел (R, S), для чого виконують таки дії: 5.1. Перший і другий користувачі генерують випадкові числа t1 = 87193323415243553115136314; t2 = 13341235311683513436277397. 5.2. Перший і другий користувачі формують значення R1 і R2 шляхом виконання операцій, що задаються формулою Ri = tiz mod p: R1 = 1965194394329054883669233593435354225553528 543048; R2 = 1801494138779005461431461992712459284574365 568004. 5.3. Перший і другий користувачі формують спільний елемент R колективногo підпису по формулі R = R1R2 mod p: R = 1510852283605141265167548142888441887806196 045589. 5.4. Генерують допоміжне БДЧ Е по формулі Е = RH mod d, де додаткове просте БДЧ d = 35488784369499179: E = 284568 і7839200835. 5.5. Перший і другий користувачі формують значення S1 і S2 шляхом виконання операцій, що задаються формулою Sі = kiEti mod p: S1 = k1E mod p = 4148535211232159148126798091089939732985696 617514; S2 = k2Et2 mod p = 2730162064644391187089975280681531058188325 016451. 5.6. Формують елемент S колективного підпису шляхом перемножування значень S1 і S2, тобто по формулі S = S1S2 mod p: S = 8419167629556847701157133962958060184058127 98449. 6. Формують перше перевірочне БДЧ А по формулі А = Sz mod p: А = 3706556715611998607017386135859762149957976 034058. 7. Формують друге перевірочне БДЧ B, для чого виконують такі дії. 7.1. Обчислюють колективний відкритий ключ, відповідний першому і другому користувачам, по формулі Р = Р1Р2 mod p: Р = 2990134734103360572197713807958838985734800 097971. 7.2. Обчислюють друге перевірочне БДЧ В по формулі В = PE R mod p: PE mod p = 9404648022790596453442388339576209856382793 42075; 23 В = PER mod p = 3706556715611998607017386135859762149957976 034058. 8. Порівнюють (наприклад, порозрядне) параметри першого і другого перевірочних БДЧ А і В. Порівняння показує, що параметри БДЧ А і В співпадають, що указує на достовірність колективного ЕЦП, що належить першому і другому користувачам, яка означає, що документ, представлений БДЧ H, підписаний як першим, так і другим користувачами. Це доводиться теоретично таким чином. Для ЕЦП, сформованого з використанням правильного значення секретного ключа маємо: S = S1S2 = (k1Et1)(k2Et2) = (k1k2)E(t1t2 ) mod p Þ Sz = (k1k2)zE (ttt2)z = (k1zk2z)E (t1zt2z) = PE R mod p, тобто для колективного ЕЦП, сформованого з використанням секретних ключів першого і другого користувачів відповідно до процедур прикладу, рівняння перевірки підпису виконується. Даний приклад ілюструє спосіб по п. 1 відповідно до варіанту реалізації по п. 5 формули корисної моделі. Цей варіант реалізації способу забезпечує ЕЦП скороченого розміру при використовуванні обчислень по простому модулю. В даному прикладі генерують колективний ЕЦП, в якому одне з БДЧ, складових підпис (Е, S), має зменшену довжину, що дозволяє скоротити загальний розмір підпису. 11 Формують просте число, таке ще р - 1 містить квадрат великого простого числа z, тобто р = Nz2 + 1, де N - парне число: р = 4153476369892465269012870897623282390047400 100719, де z = 132104433635297779312031; N = 238. 2. Формують секретний ключ у вигляді випадкового БДЧ k1, k2 i k3: k1 =3526378981324543353612; k2 = 5161833476248544287957 k3 = 1134645756882454332351. 3. Формують відкриті ключі трьох користувачів у вигляді БДЧ Р1, Р2 і Р3, відповідно, по формулі Р1 = kiz mod p: Р1 = 3864858100219352940369774847788552018367055 197706; Р2 = 1114137187563681248610918988022794167097659 20068; Р3 = 1007524924840372827951240203079659934380448 88870. 4. Приймають ЕД, представлений, наприклад, БДЧ H (як Н може бути узята, зокрема, хєшфункція від ЕД): Н = 73568790119017231823457. 5. Формують ЕЦП у вигляді пари чисел (R, S), для чого виконують таки дії: 5.1. Перший і другий користувачі генерують випадкові числа t a 1 = 87193323415243553115136314; 31105 24 t a 2 = 13341235311683513436277397. де a 1 = 1 і a 2 = 3. 5.2. Перший і другий користувачі формують значення R a 1 і R a 2 шляхом виконання операцій, що задаються формулою R a j = t a j z mod p: R a1 = 1965194394329054883669233593435354225553528 543048; R a2 = 1801494138779005461431461992712459284574365 568004. 5.3. Перший і третій користувачі формують спільний елемент R по формулі R = R a 1 R a 2 mod p: R = 1510852283605141265167548142888441887806196 045589. 5.4. Генерують перше БДЧ колективного підпису у вигляді БДЧ Е, обчислюваного по формулі Е = RH mod d, де d - додаткове просте БДЧ d = 35488784369499179: Е = 28456867839200835. 5.5. Перший і другий користувачі формують значення S a 1 i S a 2 шляхом виконання операцій, що задаються формулою S a j = k a j Et a j mod p, де j = 1, 2, a 1 = 1 i a 2 = 3. S a1 = 4148535211232159148126798091089939732985696 617514; S a2 = 2730162064644391187089975280681531058188325 016451. 5.6. Формують елемент S колективного підпису шляхом перемножування значень S a 1 i S a 2 , тобто по формулі S = S a 1 S a 2 mod p: S = 8419167629556847701157133962958060184058127 98449. 6. Формують перше перевірочне БДЧ А, для чого виконують такі дії. 6.1. Обчислюють колективний відкритий ключ, відповідний першому і другому користувачам, по формулі Р = P a 1 P a 2 mod p, де р, де j = 1, 2, a 1 = 1 i a 2 = 3: Р = 2990134734103360572197713807958838985734800 097971. 6.2. Обчислюють друге перевірочне БДЧ A по формулі A = (Sz P-E mod p) H mod d = (SzPp-E-1 mod p) H mod d: Sz mod p = 3706556715611998607017386135859762149957976 034058. 25 31105 р – Е 1 mod p = 4153476369892465269012870897623251494548845 697444; Pp-E-1 mod p = 2679999797861322305674427829882033914804034 959774; E’ = SzPp-E-1 mod p = = 1510852283605141265167548142888441887806196 045589; A = E’H mod d = 28456867839200835. 7. Формують друге перевірочне БДЧ В = Е: В = Е = 28456867839200835. 8. Порівнюють (наприклад, порозрядне) параметри першого і другого перевірочних БДЧ А і В. Порівняння показує, що параметри БДЧ А і В співпадають, що указує на достовірність колективного ЕЦП, тобто прийнятий колективний ЕЦП відноситься до прийнятого ЕД, представленого БДЧ Н, і сформован першим і третім користувачами, яким відповідає колективний відкритий ключ, рівний добутку їх відкритих ключів, узятому по модулю р. Достовірність колективної ЕЦП, що належить першому і третьому користувачам, означає, що документ, представлений БДЧ Н, підписаний як першим, так і третім користувачами. Даний приклад ілюструє спосіб по п.1 відповідно до варіанту реалізації по п. 6 формули корисної моделі. Цей варіант реалізації способу забезпечує скорочення двох БДЧ, складових ЕЦП, при використовуванні обчислень по простому модулю. Для скорочення прикладу розглядається формування колективного ЕЦП у вигляді двох БДЧ Е і S, що відноситься до двох користувачів, проте аналогічним чином можна сформувати і перевірити колективний ЕЦП, що відноситься до довільного числа користувачів. 1 Формують просте число, таке ще р - 1 містить квадрат простий множник q, тобто р = N’q + 1, де N’ - парне число: р = 4153476369892465269012870897623282390047400 100719, де q = 132104433635297779312031; N’ = 31440855205200871476263378. 2. Формують секретний ключ у вигляді випадкового БДЧ k1 =3526378981324543353612; k2 = 1134645756882454332351. 3. Формують відкриті ключі першого і другого користувачів у вигляді БДЧ Р1 і Р2, відповідно, для чого виконують таку послідовність дій: 3.1. Генерують додаткове БДЧ g по формулі g = a N’ mod p, де a - випадкове вибиране число, a = 174658: g = 1092542652057354083616996599448449105489307 509155. Одержане додаткове БДЧ g має порядок q, тобто для нього виконується умова gq mod p = 1. 3.1. Генерують по формулі Pi = g ki mod p, 26 Р1 =34333345685377125409139461980200482717001 91416922; Р2 = 3863994385639455596779422037635001482560125 596243. 4. Приймають ЕД, представлений, наприклад, БДЧ H (як Н може бути узята, зокрема, хєшфункція від ЕД): Н = 73568790119017231823457. 5. Формують ЕЦП у вигляді пари чисел (R, S), для чого виконують таки дії: 5.1. Перший і другий користувачі генерують випадкові числа t1 = 87193323415243553115136314; t2 = 13341235311683513436277397. 5.2. Перший і другий користувачі формують значення R1 і R2 шляхом виконання операцій, що ti задаються формулою Ri = g mod p: R1 = 3102767354750932471126071618632117690989549 467953; R2 = 2736650920704529583192747848763794868154802 175076. 5.3. Перший і другий користувачі формують спільне значення R12 формулі R12 = R1R2 mod p: R12 = 4612496234286267156330124112707228125194401 2875. 5.4. Генерують допоміжне БДЧ Е по формулі Е = R12H mod d, де додаткове просте БДЧ d = 35488784369499179: E = 1310719285759554. 5.5. Перший і другий користувачі формують значення S1 і S2 шляхом виконання операцій, що задаються формулою Sі = Еki mod q: S1 = Ek1 + t1 mod q = 728310863573296830603; S2 = Ek2 + t2 mod q = 56086667770983024235244. 5.6. Формують елемент S колективного підпису шляхом складання значень S1 і S2, тобто по формулі S = S1+S2 mod q: S = 56814978634556321065847. 6. Формують перше перевірочне БДЧ А, для чого виконують такі дії. 6.1. Обчислюють колективний відкритий ключ, відповідний першому і другому користувачам, по формулі Р = Р1Р2 mod p: Р = 1068337436654462125071874310676734040823302 350399. 6.2. Обчислюють перше перевірочне БДЧ А по формулі А = (gSP-Е mod p) H mod d = (gSPq-E mod p) H mod d: gS mod p = 2990618275667070987781223980090375140414481 497689; q-E = 132104432324578493552477; Pq-E mod p = 3230608368485602937575106171851890664155052 154957; 27 31105 E’ = gsPq-E mod p = 4612496234286267156330124112707228125194401 2875; A = E’H mod d = 1310719285759554. 7. Формують друге перевірочне БДЧ В = Е: B = R= 1310719285759554. 8. Порівнюють (наприклад, порозрядне) параметри першого і другого перевірочних БДЧ А і В. Порівняння показує, що параметри БДЧ А і В співпадають, що указує на достовірність колективного ЕЦП, тобто прийнятий колективний ЕЦП відноситься до прийнятого ЕД, представленому БДЧ Н, і сформований двома користувачами, яким відповідає колективний відкритий ключ, рівний добутку відкритих ключів цих користувачів, узятому по модулю р. Достовірність колективного ЕЦП, що належить першому і другому користувачам, означає, що документ, представлений БДЧ H, підписаний як першим, так і другим користувачами. У цьому прикладі перевірка достовірності колективного ЕЦП фактично здійснюється по формулах Е’ = у-EgS mod р, A = Е’Н mod d, В = Е и А = В. Коректність процедур формування і перевірки підпису доводиться для довільних розмірів БДЧ, використаних в даному прикладі, таким чином: А = Е’Н mod d = (y-EgS mod p) H mod d = (y-EgS mod p) H mode) d = ((g -Ek 1 g -Ek 2 ) g Ek 1 + t 1 + Ek 2 + t 2 t1 +t 2 t1 t2 mod p) H mod d = ((g mod p) H mod d = (g g mod р) Н mod d = (R1R2 mod p) H mod d = R12H mod d = E = B, Даний приклад ілюструє спосіб по п. 1 відповідно до варіанту реалізації по п. 7 формули корисної моделі. Цей варіант реалізації способу забезпечує формування колективного ЕЦП у вигляді двох БДЧ Е і S, що відноситься до двох різних електронних документів. 1 Формують просте число, таке ще р - 1 містить квадрат простий множник q, тобто р = N’q + 1, де N’ - парне число: р = 4153476369892465269012870897623282390047400 100719, де q = 132104433635297779312031; N’ = 31440855205200871476263378. 2. Формують секретний ключ у вигляді випадкового БДЧ k1 =3526378981324543353612; k2 = 1134645756882454332351. 3. Формують відкриті ключі першого і другого користувачів у вигляді БДЧ Р1 і Р2, відповідно, для чого виконують таку послідовність дій: 3.1. Генерують додаткове БДЧ g по формулі g = a N’ mod p, де a - випадкове вибиране число, a = 174658: g = 1092542652057354083616996599448449105489307 509155. Одержане додаткове БДЧ g має порядок q, тобто для нього виконується умова gq mod p = 1. 3.1. Генерують по формулі Pi = g ki mod p, 28 Р1 =34333345685377125409139461980200482717001 91416922; Р2 = 3863994385639455596779422037635001482560125 596243. 4. Приймають два різних ЕД, представлених, наприклад, БДЧ Н1 і Н2 (як H1 i Н2 можуть бути узяті хєш-функції від цих ЕД): H1 = 73568790119017231823457; Н2 = 13149608197092831584251. 5. Формують колективний ЕЦП у вигляді пари чисел (E,S), для чого виконують такі дії: 5.1. Перший і другий користувачі генерують випадкові числа t1 = 87193323415243553115136314; t2 = 13341235311683513436277397. 5.2. Перший і другий користувачі формують значення R1 і R2 шляхом виконання операцій, що ti задаються формулою Ri = g mod p: R1 = 3102757354750932471126071618632117690989549 467953; R2 = 2736650920704529583192747848763794868154802 175076. 5.3. Перший і другий користувачі формують спільне значення R12 по формулі R12 = R1R2 mod p: R12 = 4612496234286267156330124112707228125194401 2875. 5.4. Генерують елементі: колективного підпису у вигляді БДЧ, обчислюваного по формулі Е = R12 mod d, де d - додаткове просте БДЧ d = 35488784369499179: Е = 26024-955527428098. 5.5. Перший і другий користувачі формують значення S1 і S2 шляхом виконання операцій, що задаються формулою Si = ЕНiki + ti mod q: S1 =EH1k1 + t1 mod q = 3051416462327757619576; S2 = EH2k2 + t2 mod q = 46817971001761204206038. 5.6. Формують елемент S колективного підпису шляхом складання значень S1 і S2, тобто по формулі S = S1 + S2 mod q: S = 49869387464088961825614. 6. Формують перше перевірочне БДЧ А, для чого виконують такі дії. 6.1. Обчислюють колективний відкритий ключ, відповідний першому і другому користувачам, по 2 формулі P = Õ PiHi mod p: i= 1 H P1 1 = 3192986188590902019279100599364423667717869 234748; H P2 2 = 2145653218157257256253605149794108318708675 776011; 29 Р = 6079864693960582261609654640549111122716292 31480. 6.2. Обчислюють перше перевірочне БДЧ А по формулі А = (g SP-E mod p) mod d = (gSPq-E mod p) mod d: gS mod p 1163681247088626411656537018750571580687406 192371; q-E = 132104407610332251883933; Pq-E mod p = 9364694995266377794323919648556327776297999 50691; E’ = gSPq-E mod p = 4612496234286267156330124112707228125194401 2875; A = E’ mod d = 26024965527428098. 7. Формують друге перевірочне БДЧ В по формуле В = Е: В = 26024965527428098. 8. Порівнюють (наприклад, порозрядне) параметри першого і другого перевірочних БДЧ А і В. Порівняння показує, що параметри БДЧ А і В співпадають, що указує на достовірність колективного ЕЦП, тобто прийнятий ЕЦП відноситься до прийнятого ЕД, представленому БДЧЯ, сформований двома користувачами, яким відповідає колективний відкритий ключ, рівний добутку відкритих ключів цих користувачів, зведених по модулю p в ступінь Н1 і Н2, відповідно. Достовірність колективного ЕЦП, що належить першому і другому користувачам, означає, що документ, представлений БДЧ H1 підписаний першим користувачем, а документ, представлений БДЧ Н2, підписаний другим користувачем. Розглянуті приклади експериментально підтверджують коректність реалізації способу, якій заявляється, що доповнює приведені вище математичні докази коректності описаних конкретних реалізацій заявленого способу формування і перевірки колективного ЕЦП, якій завіряє ЕД. Таким чином, показано, що спосіб, що заявляється, може бути встановлений в основу стійких систем колективного ЕЦП, що забезпечують зменшення розміру колективного ЕЦП. Приведені приклади і математичне обґрунтовування показують, що пропонований спосіб формування і перевірки достовірності ЕЦП працює коректно, технічно реалізовуваний і дозволяє досягти сформульованого технічного результату. Перелік посилань 1. Иванов М.А. Криптографические методы защиты информации в компьютерных системах и сетях. –М.: КУДИЦ-ОБРАЗ, 2001. - 368с. 2. Ростовцев А.Г., Маховенко Е.Б. Введение в криптографию с открытым ключом. - С-Петербург: Мир и семья, 2001. 3. Молдовян А.А., Молдовян Н.А., Советов Б.Я. Криптография. - СПб.: Лань, 2000, - 224с. 4. Молдовян Н.А. Практикум по криптосистемам с открытым ключом. - СПб.: БХВПетербург, 2007. - 304с. 31105 30 5. Б.Я. Рябко, А.Н. Фионов. Криптографические методы защиты информации. -М.: Горячая линия - Телеком, 2005. - 229с. 6. Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи. Государственный стандарт Российской Федерации ГОСТ Р 34.10-2001. - 12с.
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for forming and checking authenticity of a collective signature for electronic document authenticity
Автори англійськоюKarpukov Leoind Matviiovych, Kozina Halyna Leonidivna, Moldovian Oleksandr Andriiovych, Moldovian Mykoloa Andriiovych
Назва патенту російськоюСпособ формирования и проверки достоверности коллективной электронной подписи для заверения электронного документа
Автори російськоюКарпуков Леонид Матвеевич, Козина Галина Ленидовна, Молдовян Александр Андреевич, Молдовян Николай Андреевич
МПК / Мітки
МПК: G09C 1/00, H03M 5/00, H03M 7/00
Мітки: цифрового, перевірки, достовірності, колективного, засвідчення, підпису, документа, електронного, спосіб, формування
Код посилання
<a href="https://ua.patents.su/15-31105-sposib-formuvannya-i-perevirki-dostovirnosti-kolektivnogo-elektronnogo-cifrovogo-pidpisu-dlya-zasvidchennya-elektronnogo-dokumenta.html" target="_blank" rel="follow" title="База патентів України">Спосіб формування і перевірки достовірності колективного електронного цифрового підпису для засвідчення електронного документа</a>
Попередній патент: Тепловий акумулятор
Наступний патент: Мікропроцесорна система керування тяговою передачею локомотива
Випадковий патент: Спосіб вибухового зміцнення та плакування зубів ковшів екскаваторів












