Спосіб виконання ортогональних перетворень зображень по базису хаара

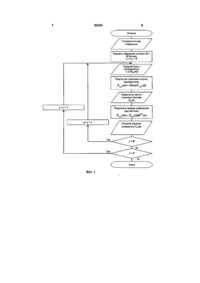
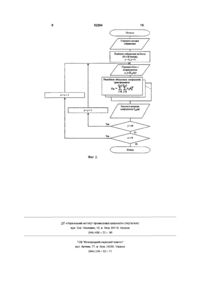
Спосіб виконання ортогональних перетворень зображень по базису Хаара, що складається з Запропонований винахід відноситься до автоматики й обчислювальної техніки і може бути використаний, зокрема, у системах обробки і відображення інформації Відомий спосіб виконання ортогональних перетворень зображень по базису Хаара [ 1 , 2], який складається з наступних етапів розгортання зображення в одномірну ПОСЛІДОВНІСТЬ, ПОДІЛ отриманої ПОСЛІДОВНОСТІ на відрізки визначеної довжини, виконання прямого ортогонального перетворення Хаара над кожним з отриманих відріз операцій поділу зображення на блоки визначеної розмірності та виконання ортогонального перетворення над кожним з отриманих блоків, який відрізняється тим, що ортогональні перетворення над блоками виконуються за один етап з рівнобіжним обчисленням необхідних коефіцієнтів трансформанти за рахунок використання двовимірного базису Хаара І 1 1 І 1 І 1 л/2 V2 - Л -л/2 О о о 2-2 І # де N - КІЛЬКІСТЬ елементів вектора ВІДЛІКІВ, N= 2", п =1,2, З, Н(п) - матриця Хаара розмірністю NxN, яка формується в результаті дискретизації перших N функцій Хаара, Х(п) - вектор (відрізок) ВІДЛІКІВ зображення, Y(n) - вектор коефіцієнтів перетворення Хаара Матриця Хаара Н(п) для N=8 має вид О ft о V 4Г 2 0 0 0 0 0 -2 0 0 0 1 1 - 1 - 1 - 1 - 1 ків ВІДПОВІДНО до виразу Г(«) 1 9 0 ~4І 0 -2 0 0 0 -& 0 (1 Недоліками відомого способу є необхідність розгортання зображення в одномірну послідовність, що збільшує час виконання перетворення, можливість обліку тільки одномірних кореляційних зв'язків уздовж розгортай, чого не досить для більшості задач обробки зображень Найбільш близьким до запропонованого технічним рішенням, обраним як прототип, є спосіб виконання ортогональних перетворень над зображеннями по базису Хаара [3], заснований на властивості подільності ортогональних базисів, який складається з наступних етапів поділ всього двовимірного масиву відліків зображення на блоки розмірності NxN, виконання перетворення Хаара (ПХ) над стовпцями блоку відліків зображення, результатом якого є проміжна матриця, виконання ПХ над рядками проміжної матриці, результатом якого є матриця коефіцієнтів Хаара Зазначені процедури описуються наступним виразом (О ю 52264 т Y(n) N' -Щп)Х(п)Н (п) , де X(n) - матриця ВІДЛІКІВ зображення (блок розмірністю NxN), Н(п) - матриця Хаара розмірністю NxN, Нт(п) -транспонована матриця Хаара, Y(n) - матриця коефіцієнтів перетворення Хаара (трансформанта розмірності NxN) Недоліками даного способу є необхідність виконання перетворення Хаара в два етапи, що спричиняє - збільшення помилок округлення, тому що помилки, сформовані на першому етапі, беруть участь в арифметичних операціях другого етапу, - неможливість початку виконання процедур другого етапу перетворення до закінчення виконання всіх процедур першого етапу, що збільшує час виконання перетворення, - необхідність виділення додаткової пам'яті під збереження проміжної матриці, - обмеженість у можливостях рівнобіжного виконання процедур перетворення, що не дозволяє зменшити час, який необхідний для виконання перетворення, - неможливість одержання тільки частини коефіцієнтів Хаара В основу винаходу поставлена задача створити спосіб виконання ортогональних перетворень зображень по базису Хаара, який дозволив би рівнобіжне виконання більшості процедур перетворення без ускладнення алгоритму перетворення й додаткових витрат пам'яті, що зменшить час виконання перетворення Поставлена задача вирішується за рахунок того, що пропонується спосіб виконання ортогонального перетворення зображення по базису Хаара, який ґрунтується на двовимірному базисі Хаара Далі будемо називати цей спосіб - двовимірним Я 0,0 Лп Яге Щг і*|з Н1Х ід Нгг Я 2 3 Я 2 4 #2s # Ї ( І Я 2 7 ur IT tr ст аы Н15 Щ6 я„ я„ я3 4 я зо #50 #46 #51 #52 #53 #54 # 5 Я-jc V— - вектор-стовпець, отриманий транспоk нуванням k-ro рядка матриці Н(п), V| - вектор-рядок, яка являє собою 1й рядок матриці Н(п), ® - символ кронекеровського добутку Нижче приведені деякі з підматриць матриці (п) для N=8 1 1 1 —I -1 _! _ і - 1 1 1 1 - 1 1 _1 —1 1 1 1 1 1 1 1 1 1 -1 1 — 1 —1 1 1 1 1 1 1 1 1 1 - 1 — 1 - 1 1 1 1 1 1 1 1 -1 _1 „I — 1 —1 І 1 1 1 1 1 1 1 Ї 1 — 1 — 1 _1 1 І 1 """ А — 1 1 1 1 -1 - 1 - 1 1 1 1 1 1 1 1 _ 1 _1 І 1 1 1 1 1 1 1 1 1 1 _ і _ 1 _1 —1 —1 _ 1 — 1 -1 — 1 —1 —1 -1 — 1 _1 —1 1 1 1 1 _ 1 1 1 1 _1 —1 —\ _1 —1 — 1 — 1 — І -1 —1 —1 Н77J ра Нпр2(п) з координатами к, І = 0, N - 1 , 1 1 1 Я'76 де Нк,І - підматриця двовимірної матриці Хаа 1 1 1 1 #56 #57 де Нк,І - матриця, яка представляє собою дискретні значення однієї з двовимірних функцій базиса Хаара й визначає ВІДПОВІДНИЙ коефіцієнт Хаара Процедура отримання підматриць Hk,l описується виразом 1 1 1 1 #« #66 #67 Ям 1 1 1 IT И]7 #36 #37 1 1 1 Н, '06 її 1 1 1 1 я, Я Япе а 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 _J #00 #01 #02 #03Нлл І-Ч 1 1 1 1 1 1 4 перетворенням Хаара (ДвПХ) Двовимірний базис Хаара описується клітин2 2 2 ною матрицею Нпр (п) розмірністю N xN , яка складається з підматриць Hk,l розмірності NxN й для N=8 має вид 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 в 0 2 2 2 2 2 2 2 -2 -2 -2 -2 -2 -2 0 0 0 0 0 0 0 0 0 0 0 0 _1 - 1 0 0 0 0 0 0 2 52264 Технічний результат, який може бути отриманий при здійсненні винаходу, полягає в усуненні двоетапності процедури перетворення і застосуванні рівнобіжного виконання більшості процедур перетворення На фиг 1 приведена блок-схема алгоритму, що реалізує спосіб, який прийнято за прототип На рис 2 приведена блок-схема алгоритму, яка реалізує запропонований спосіб Суть способу, що пропонується полягає в наступному Для виконання ортогонального перетворення необхідне виконання таких процедур поділ всього масиву ВІДЛІКІВ зображення на блоки розмірністю NxN, виконання ДвПХ над кожним із блоків зображення ВІДПОВІДНО до виразу ЛГ-liV-l Е * ij J £ J ' « -g if I Ч ij де Х, | Укі елемент h кі ' « J люватися рівнобіжно, що дозволить істотно зменшити час, необхідний для виконання перетворення Хаара ВІДПОВІДНО ДО блок-схеми (фиг 2) алгоритм складається з наступних процедур отримання зображення, поділ зображення на блоки необхідної розмірності, в результаті чого отримаємо N блоків по вертикалі і М - по горизонталі, організація циклу, в якому обробляється кожний із блоків, при цьому х і у - лічильники циклу, умова виходу з циклу - x>N і у>М В ТІЛІ циклу виконується рівнобіжне обчислення необхідних коефіцієнтів трансформанти - поелементне перемноження відповідної підматриці двовимірного базису та блоку ВІДЛІКІВ, сумування отриманих значень й запис їх у пам'ять Після обробки всіх блоків зображення (виконання умови виходу з циклу) отримаємо масив коефіцієнтів Хаара для вихідного зображення й алгоритм припиняє свою роботу елемент блоку зображення, трансформанти Хаара, елемент підматриці Ни, к, l,i,j = 0,N - 1 | J Результатом останнього виразу є один з коефіцієнтів трансформанти Хаара Дана процедура виконується для кожної з підматриць Нкі при необхідності отримати всі коефіцієнти трансформанти Хаара, або тільки для тих коефіцієнтів, в яких є потреба Результатом всіх процедур є матриця коефіцієнтів Хаара Всі коефіцієнти можуть обчис Література 1 Залмазон Л А Преобразования Фурье, Уолша, Хаара и их применение в управлении, связи и других областях - М Наука, 1989 - С 219227 2 Ахмед Н , Рао К Р Ортогональные преобразования при обработке цифровых сигналов Пер с англ / Под ред И Б Фоменко - М Связь, 1 9 8 0 - С 148 3 Ахмед Н , Рао К Р Ортогональные преобразования при обработке цифровых сигналов Пер с англ / Под ред И Б Фоменко - М Связь, 1980 - С 159 52264 Початок Отримати вихідне зображення Поділити зображення на блоки (N\ М блоків), Отримати блок з координатами Розрахунок проміжної матриш {перший етап). Записати до пам'яті проміжну матрицю Розрахунок матриці коефішєнпв (другий етап) Записати матрицю коефіцієнтів YgJn) Фиг. І. 52264 10 Початок Отримати вихідне зображення Поділити зображення на блоки (NxM блоків), Отримати блок з координатами Рівнобіжне обчислення коефіцієнтів транеформанти Записати матрицю коефіцієнтів YxJn) Фиг. 2. ДП «Український інститут промислової власності» (Укрпатент) вул Сім'ї Хохлових, 15, м Київ, 04119, Україна ( 0 4 4 ) 4 5 6 - 2 0 - 90 ТОВ "Міжнародний науковий комітет" вул Артема, 77, м Київ, 04050, Україна (044)216-32-71