Спосіб паралельного алгебраїчного додавання тривалостей групи часових інтервалів

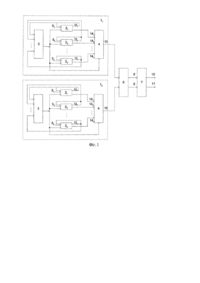
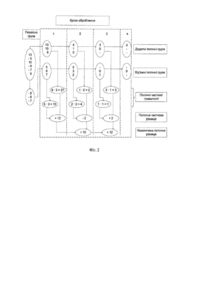
Винахід відноситься до автоматики та обчислювальної техніки і може бути використаний в операційних схемах аналогових процесорів, а також при вирішенні задач визначення нулів та екстремумів функцій, які задані таблицею. Відомий спосіб паралельного додавання тривалостей групи часових інтервалів (Карпов Р.Г., Карпов М.Р. Преобразование и обработка широтно-импульсных сигналов. М., « Машиностроение», 1977, с. 71), який оснований на перетворенні тривалостей у напруги, підсумовуванні напруг і виділенні середнього значення суми на загальному періоді проходження групи часових інтервалів. Недоліком даного способу є обмежені функціональні можливості через те, що даний спосіб оброблює лише невід'ємні тривалості групи часових інтервалів. Відомий спосіб паралельного додавання тривалостей групи часових інтервалів (а. с. СРСР №388269, кл. G06G7/14, 1971), який оснований на накопиченні кратних тривалостей і полягає в тому, що для кожного часового інтервалу групи виділяють шляхом диференціювання моменти часу його початку і кінця, за виділеними моментами часу визначають поточне значення різниці між сумою моментів часу початку тимчасових інтервалів групи і сумою моментів часу закінчення інтервалів групи, тривалість найбільшого часового інтервалу групи перетворюють у послідовність кратних тривалостей шляхом її множення на отримане значення різниці, при цьому кратні тривалості накопичують. Недоліком даного способу є обмежені функціональні можливості через те, що даний спосіб виконує лише накопичення тривалостей часових інтервалів. Найбільш близьким по технічній суті до способу, який пропонується, є спосіб паралельного додавання тривалостей групи часових інтервалів (а. с. СРСР №1119035, кл. G06G7/14, 1984), який оснований на накопиченні кратних тривалостей, причому порівнюють між собою тривалості часових інтервалів групи і виділяють часовий інтервал найменшої тривалості, формують тривалість, яка в подальшому позначається як поточна часткова тривалість, яка є кратною цій найменшій тривалості шляхом її множення на кількість часових інтервалів у гр упі, формують нову груп у часови х інтервалів шляхом віднімання цієї найменшої тривалості від тривалості кожного часового інтервалу попередньої групи, далі зазначені дії повторюють для кожної нової групи часових інтервалів до виділення інтервалу найменшої тривалості, яка дорівнює нулю, а отримані кратні тривалості послідовно підсумовуються. Недоліком цього способу є обмежені функціональні можливості через те, що в процесі підсумовування даний спосіб не враховує розмірності первісної групи, її структури, а також і те, що серед елементів даної групи можуть бути від'ємні, поява яких призводить до зупинки оброблення груп часових інтервалів даним способом. В основу винаходу поставлено задачу створення способу паралельного алгебраїчного додавання тривалостей групи часових інтервалів, в якому за рахунок введення нових дій досягається можливість паралельного формування суми додатних та від'ємних тривалостей гр упи часових інтервалів, що призводить до розширення функціональних можливостей способу шляхом зняття обмеження на невід'ємність даних тривалостей. Поставлена задача вирішується тим, що у способі паралельного додавання тривалостей групи часових інтервалів, який оснований на накопиченні кратних тривалостей, причому у групі часових інтервалів порівнюють між собою тривалості і виділяють часовий інтервал найменшої тривалості, формують поточну часткову тривалість, яка є кратною цій найменшій тривалості, шляхом множення її на кількість часових інтервалів у групі, формують нову поточну гр уп у часових інтервалів шля хом віднімання цієї найменшої тривалості від тривалості кожного часового інтервалу попередньої групи, далі зазначені дії повторюють для кожної нової поточної групи часових інтервалів до виділення інтервалу найменшої тривалості, яка дорівнює нулю, спочатку первісну групу часових інтервалів поділяють на додатну і від'ємну за знаком тривалості групи, у кожній групі одночасно виконують формування поточної часткової тривалості і нової поточної групи часових інтервалів, формують поточну часткову різницю між отриманими поточними частковими тривалостями, а отримані поточні часткові різниці тривалостей з урахуванням знаку додаються. На фіг.1 зображена блок-схема пристрою, який реалізує спосіб паралельного алгебраїчного додавання тривалостей групи часових інтервалів, на фіг.2 схематично представлено паралельне алгебраїчне додавання тривалостей групи часових інтервалів 13, -5, 15, -8, -7, 9. Пристрій (фіг.1), що реалізує даний спосіб паралельного алгебраїчного додавання тривалостей групи часових інтервалів містить, два блоки 11 і 12 відповідно для оброблення додатної та від'ємної груп часових інтервалів, причому кожний блок 11 і 12 містить схеми 21, 22, ..., 2n віднімання (де n - максимальна кількість тривалостей в групі часових інтервалів), за допомогою яких виділяють різниці між тривалостями окремих інтервалів групи та інтервалами найменшої тривалості, схему 3 порівняння, де виділяються інтервали найменшої тривалості, схему 4 послідовного додавання (накопичення) кратних тривалостей, в якому також виконується множення найменших тривалостей на кількість часових інтервалів у поточній групі, входи 51, 52, ..., 5n, на які подаються тривалості часових інтервалів первісної групи. Крім того, пристрій містить схему 6 віднімання, де формуються поточні часткові різниці між отриманими поточними частковими тривалостями, та схему 7 послідовного підсумовування (накопичення) отриманих поточних часткових різниць з їхніми знаками "+" або "-" відповідно у випадку, коли поточна часткова суш тривалостей додатної групи перевищує поточну часткову суму тривалостей від'ємної гр упи або навпаки. При цьому схема 7 послідовного додавання має інформаційний вхід 8, знаковий вхід 9 та ін формаційний вихід 10 і знаковий вихід 11, які є виходами пристрою. У кожному блоці 11 і 12 інформаційні виходи 121, ..., 12n схем 21, 22, ..., 2n віднімання з'єднані з входами схеми 3 порівняння і першою групою входів схем 2 1, 22, ..., 2n віднімання, які також підключені до входів 51, 52, ..., 5n пристрою. Другі входи схем 21, 22,..., 2n віднімання з'єднані з виходом 13 схеми 3 порівняння, який також підключений до входу схеми 4 послідовного додавання. Виходи ознак схем 21, 22, ..., 2n віднімання з'єднані з групою входів 141, ..., 14n схеми 4 послідовного додавання. Виходи 15 схеми 4 послідовного додавання обох блоків 11 і 12 підключені відповідно до входів схеми 6 віднімання, інформаційний та знаковий виходи якої з'єднані відповідно з входами 8 і 9 схеми 7 послідовного підсумовування. Паралельне алгебраїчне додавання тривалостей групи часових інтервалів виконується в такий спосіб. Спочатку поділяють первісну груп у часових інтервалів відповідно за знаком на дві групи: додатну та від'ємну, після чого знак тривалостей від'ємної групи змінюють на додатній шляхом множення тривалостей цієї групи на "-1". В результаті отримують дві групи часових інтервалів, до яких паралельно застосовують вище зазначені дії, а саме: на першому кроці порівнюють між собою тривалості часових інтервалів кожної групи і виділяють часовий інтервал найменшої тривалості. Формують поточну часткову тривалість, яка є кратною цієї найменшої тривалості, шляхом множення її на кількість часових інтервалів у гр упі, формують нову (др угу поточну) груп у часови х інтервалів шляхом віднімання цієї найменшої тривалості від тривалості кожного часового інтервалу попередньої групи. Формують поточну часткову різницю між двома отриманими поточними тривалостями. При цьому, якщо поточна часткова тривалість додатної групи менша за модулем ніж відповідна поточна часткова тривалість від'ємної групи, поточна часткова різниця тривалостей помножується на "-1". На другому кроці у двох гр упах часови х інтервалів повторюють зазначені дії, а саме: порівнюють між собою тривалості часових інтервалів кожної групи і виділяють часовий інтервал найменшої тривалості. Формують поточну часткову тривалість, яка є кратною цієї найменшої тривалості, шляхом множення її на кількість часових інтервалів у групі, формують нову поточну гр уп у часових інтервалів шляхом віднімання цієї найменшої тривалості з тривалості кожного часового інтервалу попередньої групи. Формують поточну часткову різницю між двома отриманими поточними тривалостями. При цьому, якщо поточна часткова тривалість додатної групи менша за модулем ніж відповідна поточна часткова тривалість від'ємної групи, поточна часткова різниця тривалостей помножується на "-1". Накопичується поточна різниця шляхом підсумовування отриманих поточних часткових різниць з урахуванням їхніх знаків. Далі зазначені дії повторюють для кожних нових (поточних) груп часови х інтервалів до виділення інтервалу найменшої тривалості, яка дорівнює нулю. Розглянемо паралельне алгебраїчне додавання, наприклад, тривалостей групи, яка складається з шести часови х інтервалів (фіг.2). Додаються інтервали з тривалостями, які дорівнюють 13, -5, 10, -8, -7, 9. Три тривалості (окремо додатні та від'ємні) подаються відповідно на входи 51, 52, і 53 кожного блока 11 і 12, внаслідок чого створюються первісні групи для додавання. Оскільки в початковому стані на виході схеми 3 порівняння обох блоків 11 і 12 присутня нульова тривалість, то на першому кроці оброблення від кожної початкової тривалості віднімається нуль зі схеми 3 порівняння, і на виходах схем 2 1, 22, і 23 формуються різниці, які фактично дорівнюють початковим тривалостям часових інтервалів. Для блока 11 це тривалості 13,10 та 9, які паралельно подаються на три входи схеми 3 порівняння, де відбувається виділення інтервалу найменшої ненульової тривалості з поданих трьох інтервалів, тобто утворюється мінімальна тривалість, а саме 9, яка подається на входи схеми 4 послідовного додавання, де формується поточна часткова тривалість 27, яка визначається кількістю тривалостей первісної додатної групи. Відповідно для блока 12 це тривалості -5, -8, та -7, які після "трансформування" у 5, 8, та 7, паралельно подаються на три входи схеми 3 порівняння, де відбувається виділення інтервалу найменшої ненульової тривалості з поданих трьох інтервалів, тобто утворюється мінімальна тривалість, а саме 5, яка подається на входи схеми 4 послідовного додавання, де формується тривалість 15, яка визначається кількістю тривалостей первісної від'ємної групи. Після отримання поточних часткових тривалостей в блоках 11 і 12 формується перша часткова різниця (27-15), а саме 12, яка з урахуванням того, що поточна часткова тривалість додатної групи більша за поточну часткову тривалість від'ємної групи, подається на схему 7 послідовного підсумовування зі знаком "+", т.т. перша різниця дорівнює +12. На другому кроці у схемах 21 , 22 , і 23 блока 11 формуються різниці між початковими тривалостями 13, 10 і 9 та мінімальною тривалістю першої групи, яка дорівнює 9, Утворюються різниці 4, 1 і 0 другої групи. Найменша ненульова тривалість часового інтервалу другої гр упи, яка дорівнює 1, формується в схемі 3 порівняння і подається на схему 4 послідовного додавання, де формується двократна мінімальна тривалість другої гр упи, в даному випадку 2, яка є поточною частковою тривалістю додатної групи. Відповідно на другому кроці у схемах 21, 2 2, і 23 блока 12 формуються різниці між початковими тривалостями 5, 8 і 7 та мінімальною тривалістю першої групи, яка дорівнює 5. Утворюються різниці 0, 3 і 2 другої гр упи. Найменша ненульова тривалість часового інтервалу другої групи, яка дорівнює 2, формується в схемі 3 порівняння і подається на схему 4 послідовного додавання, де формується двократна мінімальна тривалість другої групи, в даному випадку 4 послідовного додавання, яка є поточною частковою тривалістю від'ємної групи. Після отримання поточних часткових тривалостей в блоках 11 і 12 формується друга поточна часткова різниця (4-2), а саме 2, яка з урахуванням того, що поточна часткова тривалість додатної групи менша за поточну часткову тривалість від'ємної групи, подається на схему 7 послідовного підсумовування зі знаком "", т.т. др уга різниця дорівнює - 2. В схемі 7 послідовного підсумовування накопичується перша різниця (122), яка дорівнює +10. На третьому кроці у схемах 21, 22, і 23 блока її формуються різниці між початковими тривалостями 4, 1 і 0 та мінімальною тривалістю другої групи, яка дорівнює 1. Утворюються різниці 3 і 0 третьої групи. Найменша ненульова тривалість часового інтервалу третьої групи, яка дорівнює 3, формується в схемі 3 порівняння і подається на схему 4 схему послідовного додавання, де формується однократна мінімальна тривалість третьої групи, в даному випадку 3, яка є поточною частковою тривалістю. Відповідно на третьому кроці у схемах 21, 22, і 23 блока 12 формуються різниці між початковими тривалостями 0, 3 і 2 та мінімальною тривалістю другої групи, яка дорівнює 2. Утворюються різниці 0, і 1 третьої групи. Найменша ненульова тривалість часового інтервалу другої групи, яка дорівнює 1, формується в схемі 3 порівняння і подається на схему 4 схему послідовного додавання, де формується однократна мінімальна тривалість третьої групи, в даному випадку 1, яка є поточною частковою тривалістю. Після отримання поточних часткових тривалостей для блоків 11 і 12 формується третя поточна часткова різниця (3-1), а саме 2, яка з урахуванням того, що поточна часткова тривалість додатної групи менша за поточну часткову тривалість від'ємної групи, подається на схему 7 зі знаком "-", т.т. +2. Формується на третьому кроці також друга накопичена поточна різниця (10+2), т.т. 12, яка є остаточним результатом. На четвертому кроці у схемах 21 , 22 , і 23 блока 11 формуються різниці між початковими тривалостями 3 і 0 та мінімальною тривалістю третьої групи, яка дорівнює 3. Утворюється різниця 0 четвертої групи. Відповідно на четвертому кроці у схемах 21, 22, і 23 блока 11 формуються різниці між початковими тривалостями 1 і 0 та мінімальною тривалістю третьої групи, яка дорівнює 1. Утворюється відповідно різниці 0 четвертої гр упи. Внаслідок того, що отримано групи з нульовими тривалостями, процес паралельного алгебраїчного додавання тривалостей даної групи часових інтервалів припиняється. Працездатність даного способу представимо доведенням наступного твердження. Твердження. Сума елементів S довільної множини W, яка містить як додатні, так і від'ємні елементи, дорівнює модулю різниці сум її додатних та від'ємних елементів, тобто ( )( ) + + S = S+ - S- = S+ + S2 + ... + Sn - S1 + S2 + ... + Sn = 1 ( )( ) ( ) (1) + + = S1 - S1 + S+ - S - + ... + S+ - Sn £ S1 - S1 + S+ - S- + ... + S+ - S2 2 n 2 2 n n S+ S, де j , j - поточні часткові суми додатних та від'ємних елементів, j = 1 n , n - кількість як додатних так і від'ємних елементів множини W. Дрведення. Доведемо, що нерівність (1) виконується при n³2. Нехай n=2, покажемо, що (S + 1 (S + 1 )( ) + - S1 + S+ - S - £ S1 - S1 + S+ - S2 2 2 2 Припустимо, що існує така пара ( )( ) (2) + + S1 - S1 S2 - S2 ), для якої нерівність (2) не виконується, тобто ; + - S1 + S+ - S- > S1 - S1 + S + - S2 . 2 2 2 Піднесемо обидві частини останньої нерівності до квадрату, тоді, враховуючи, що "xÎR маємо |х|2= х2, отримаємо: (S + 1 - S1 ) + 2(S 2 + 1 )( )( - S1 × S+ - S - + S+ - S 2 2 2 2 ) > (S 2 + 1 ) ( 2 ) 2 + - S1 + 2 S1 - S1 × S+ - S - + S+ - S- . 2 2 2 2 Це означає, що наше припущення невірне, оскільки "xÎR:|x|³ x, а отже, нерівність (2) виконується. Припустимо, що нерівність (1) виконується при n=k, тобто має місце нерівність (S + 1 )( ) ( ) + - S1 + S+ - S - + ... + S+ - Sk £ S1 - S1 + S+ - S- + ... + S+ - S- . 2 2 k 2 2 k k Доведемо, що (1) виконується і для n=k+1, тобто виконується така нерівність (S + 1 )( ) ( ) ( ) + + + + - S1 + S+ - S - + ... + Sk - Sk + Sk +1 - S-+1 £ S1 - S1 + S+ - S- + ... + Sk - Sk + S++1 - Sk +1 . 2 2 k 2 2 k Маємо, враховуючи , що виконується нерівність (2), (S + 1 )( ) ( )( ) + - S1 + S+ - S - + ... + S+ - Sk + Sk +1 - S-+1 = 2 2 k k ( ) ( ) ( ) + + + = S1 - S1 + S+ - S- + ... + Sk - Sk + S++1 - Sk +1 £ Sk +1 - S-+1 + S+ - S1 + S+ - S- + ... + S+ - S- . 2 2 k k 1 2 2 k k На основі принципу математичної індукції можна зробити висновок, що нерівність (1) виконується при n³2, що і потрібно було довести. Зауваження. Нерівність (1) дає точний результат, тобто маємо між її лівою та правою частинами знак "=", у випадку, + S + ³ Si . В такому разі можна записати наступне: |S+ -S- |=|S+ |-|S- |. Якщо ж Si < Si , то поступаємо якщо i таким чином ( )( ) + S = S+ - S- = S+ + S+ + ... + Sn - S1 + S- + ... + S- = 1 2 2 n ( )( ) ( ) ( ) + + + = S1 - S1 + S+ - S - + ... + S+ - Si- + ... + S+ - Sn £ S1 - S1 + S+ - S- + ... - Si+ - Si- + ... + Sn - S- , i =1, n. 2 2 i n 2 2 n Запропонований спосіб дозволяє розширити функціональні можливості за рахунок поділу первісної групи часових інтервалів на додатну та від'ємну гр упи за знаком тривалостей, одночасного виконання у кожній групі формування поточної часткової тривалості і нової поточної групи часових інтервалів, формування поточної часткової різниці між отриманими поточними частковими тривалостями та підсумовування отриманих поточних часткових різниць тривалостей з урахуванням знаку.