Пристрій для множення елементів скінченних полів gf(2n)

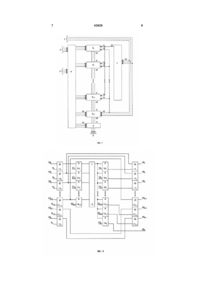
Пристрій для множення елементів скінченних полів GF(2n), який містить блок формування часткових добутків, який складається з n груп по n елементів І в кожній, (n-1) блоків матричного перетворення та блок додавання, виходи якого з'єднані з виходом результату пристрою, вхід I-го розряду першого (I=1,...,n) співмножника якого з'єднаний із згрупованими першими входами елементів І і-ої групи блока формування часткових добутків, входи поточної суми j-гo блока матричного перетворення (j=2,...,n-1) з'єднані з виходами поточної суми (j-1)-гo блока матричного перетворення, який відрізняється тим, що в нього введено блок множення, а кожний блок матричного перетворення містить першу і другу групи із n та (n-1) суматорів по модулю два, першу і другу групи з (n-2) та n елементів І та елемент АБО, причому входи блока множення з'єднані з відповідними входами коефіцієнтів утворюючого полінома пристрою і входами коефіцієнтів утворюючого полінома кожного з (n-1) блоків матричного перетворення, а виходи зі входами коефіцієнтів розширення k-го блока матричного перетворення (k=1,...,n-2), виходи поточної U 2 (19) 1 3 перетворення, блок додавання, дешифратор, n елементів И та елемент АБО та блок результату пристрою. Недоліком даного пристрою є обмеженість функціональних можливостей при виконанні операції множення, за рахунок чого зростають часові витрати при обробці інформації. Задачею корисної моделі є удосконалення пристрою для множення елементів скінченних полів шляхом видалення дешифратора та введення блоку множення. Це дозволяє забезпечити безпосередньо виконувати операції множення елементів різноманітних скінчених полів GF(2n), тобто має широкі функціональні можливості застосування їх в процедурах кодування та декодування циклічних поліноміальних кодів. Поставлена задача вирішується тим, що в пристрої для множення елементів скінченних полів GF(2n), який містить блок формування часткових добутків, який складається з n груп по n елементів И кожній, (n-1) блоків матричного перетворення та блок додавання, виходи якого з'єднані з виходом результату пристрою, вхід I-го розряду першого (I=1, ...,n) співмножника якого з'єднаний з згрупованими першими входами елементів И і-ої групи блоку формування часткових добутків, входи поточної суми j-гo блоку матричного перетворення (j=2, ...,n-1) з'єднані з виходами поточної суми (j-1)гo блоку матричного перетворення, а також, згідно з винаходом, введено блок множення, а кожний блок матричного перетворення містить першу і другу групи із n та (n-1) суматорів по модулю два, першу і другу групи з (n-2) та n елементів И та елемент АБО, причому входи блоку множення з'єднані з відповідними входами коефіцієнтів утворюючого поліному пристрою і входами коефіцієнтів утворюючого поліному кожного з (n-1) блоків матричного перетворення, а виходи зі входами коефіцієнтів розширення k-го блоку матричного перетворення (k=1, ..., n-2), виходи поточної суми (n-1)-го блоку матричного перетворення з'єднані з першими входами блоку додавання, другі входи якого з'єднані з виходами відповідних елементів И з першої по (n-1) групу якого з'єднані відповідно з входами часткових добутків з першого по (n-1) блоку формування часткових добутків, виходи якого з’єднані відповідно з входами часткових добутків, блок матричного перетворення, вхід і-го розряду другого співмножника пристрою з'єднаний з групованими другими входами і-их елементів И в кожній групі блоку формування часткових добутків, при цьому в кожному блоці матричного перетворення перші входи суматорів по модулю два першої групи з'єднані з входами поточної суми блоку, входи часткових добутків якого з'єднані з другими входами суматорів по модулю два першої групи, виходи яких, починаючи з другого, з'єднані відповідно з першими входами суматорів по модулю два другої групи, другі входи яких з'єднані з виходами з першого по (n-1)-ий елемент И другої групи, виходи суматорів по модулю два та вихід (n-2)-го елементу И другої групи з'єднані з відповідними виходами поточної суми блоку, виходи суматорів по модулю два з першого 43629 4 по (n-2)-ий першої групи з'єднані відповідно з першими входами елементів И першої групи, другі входи яких з'єднані з відповідними входами коефіцієнтів розширення блоку, а виходи з входами елемента АБО, вихід якого з'єднаний з групованими першими входами елемента И другої групи, другі входи яких з'єднані з відповідними входами коефіцієнтів утворюючого поліному блоку. Множення, наприклад, одного елементу aÎGF(pm) на другий елемент bÎGF(pm) відповідає множення багаточлену a(х) на багаточлен с(х), що відповідає елементу cÎGF(pm ), зворотному m bÎGF(p ), де багаточлен с(х) повинен відповідати умові b(х)*с(х)=1 mod p(x). Відомо [2], що множення багаточлена с(х) на багаточлен a(х) виконується у відповідності с виразом: с(х)=a(х) b(х)+r(х), яке у відповідності до того, що операції над багаточленами виконуються в полі GF(2n), то вираз можна записати у вигляді с(х)=a(х)Äb(х)År(х)=е(х)År(х), де: a(x)=am-1xm-1+am-2xm-2+...+a1x+a0; b(x)=bm-1xm-1+bm-2xm-2+...+b1x+b0; r(x)=rm-1xm-1+rm-2xm-2+...+r1х+r0; ai, bj, rs Î GF(2); e(x ) = (m-1)+(n-1) å ei xi = (n-1) å e( m -1)+ к x (m -1)+к + (m-1) (n-2) å ex = å e I I m+ к x m +к (m-1) + å ex I I . Множення елементів скінченних полів GF(2n) виконується як множення багаточленів та зводиться до обчислення суми часткових добутків з приведенням її по модулю утворюючого поліному, що забезпечує множення елементів скінченних полів GF(2n) (2≤m≤n), створених різними утворюючими поліномами. В результаті це дозволяє забезпечити безпосередньо виконувати операції множення та множення елементів різноманітних скінчених полів GF(2n), і як наслідок, розширення функціональних можливостей побудови комбінаційних схем. На креслені 1 зображена структурна схема пристрою для множення елементів скінчених полів GF(2n). На кресленні 2 - структурна схема блоку матричного перетворення. На кресленні 3 - структурна схема блоку множення. На кресленні 4 комбінаційна схема множення скінченного поля GF(2n). На кресленні 5 - приклад виконання операції множення багаточлену над полем GF(2n). Пристрій для множення елементів скінчених полів містить входи 1 коефіцієнтів утворюючого поліному, входи 2 першого співмножника, входи 3 другого співмножника, блок 4 формування часткових добутків, (n-1) блоків 5 матричного перетворення, блок 6 додавання, блоку множення 7 та виходи 8 результату. Блок 5 матричного перетворення містить входи 9 поточної суми, входи 10 часткових добутків, входи 11 поточного коефіцієнту розширення, входи 12 коефіцієнтів утворюючого поліному, першу групу з n суматорів 13 по модулю два, першу групу з (n-2) елементів И 14, (n-2) - вхідних елементів АБО 15, другу групу з n елементів И 16, другу групу з (n-1) суматорів 17 по модулю два та виходи поточної суми. i=0 k =1 l =0 k =0 l =0 5 Блок множення 7 містить входи 19 коефіцієнтів утворюючого поліному, групу з (n-3) інверторів 20, групу з (n-3) елементів И 21 та виходи 22 поточного коефіцієнту розширення. На кресленні 5 зображено приклад схеми множення багаточлену над полем GF(2n), де n=1. Пристрій для множення елементів скінчених полів GF(2n) працює в такий спосіб. Перед початком множення на входи 1 утворюючого поліному пристрою поступають значення коефіцієнтів утворюючого поліному gm (x), що призводить до формування на відповідному виході блоку множення 7 коефіцієнта розширення m. При поданні на входи 2 та 3 пристрою відповідно пер шого a(x ) та другого b(x ) співмножників на виходах блоку 4 формування часткових добутків утво a(x ) * bi , які подаються рюються часткові добутки на входи 10 часткових добутків відповідних і-тих блоків 5 матричного перетворення, входи 9 поточної суми кожного з яких з'єднані з однойменними входами 18 попереднього (і-1)-го блоку 5 матричного перетворення. На виходах 18 кожного і-го блоку 5 матричного перетворення формується і-а поточна сума як приведена по модулю утворюючого поліному сума і-го часткового добутку та a(x ) * bi Å Pn -1(x )mod gm (x ) . (і-1)-ої поточної суми, Таким чином, на виходах 19 (n-1)-го блоку 5 матричного перетворення формується поточна сума Pn-1(x ) a(x ) * bi Å Pn - 2 (x )mod gm (x ) . Остаяк сума точний результат множення елементів скінчених полів формується на виходах 8 блоку 6 підсумовування. Блок 4 формування часткових добутків, який вміщує в себе n груп по n елементів И в кожній, слугує для отримання послідовності часткових добутків виду ai(x)*bк, aі - множина коефіцієнтів першого співмножника, bк - коефіцієнт другого співмножника. На виходах елементів И перші групи формують часткові добутки а(n-1)*b(n-1), а(n-2)*b(n1), а(n-3)*b(n-1), ..., а1*b(n-1), а0*b(n-1), на виходах другої групи елементів И - а(n-1)*b(n-2), а(n-2)*b(n-2), a(n-3)*b(n2), …, a1*b(n-2), a0*b(n-2), на виходах n-ої групи елементів И - а(n-1)*b0, а(n-2)*b0, а(n-3)*b0, ..., a1*b0, a0*b0. Блок множення 7 призначений для визначення коефіцієнта розширення поля. Так, як ступінь розширення поля визначається старшим коефіцієнтом перетворюючого поліному gm(x), то поява сигналу "1" в старшому коефіцієнті утворюючого поліному трактується на виходах блоку множення як поточний коефіцієнт розширення. При цьому на всі інші входи надходить сигнал "0", та вони блокуються. 43629 6 Блоки 5 матричного перетворення обчислюють поточну суму часткових добутків та приведення її по модулю утворюючого поліному gm (x). Об a(x ) * bi Å Pn -1(x ) числення поточної суми , де a(x ) коефіцієнти першого співмножника, bi - і-тий коефіцієнт другого співмножника, який відповідає номеру і-го поточного блоку 5 матричного пере P (x ) - коефіцієнти поточної суми (і-1)творення, n-1 го попереднього блоку 5 матричного перетворення, Å сума по модулю два, яка виконується першою групою суматорів 13 по модулю два. Приведення по модулю два утворюючого поліному gm(x) виконується за умови якщо, сума по модулю два ак*b1Å P(i-1)=1/ак та Р(і-1) відповідно к-ті коефіцієнти першого співмножника та поточної суми попереднього блоку 5 матричного перетворення співпадає зі значенням коефіцієнта розширення поля ("1"), то a(x ) * bi Å Pn -1(x ) з суми вираховується значення коефіцієнтів gm(x) утворюючого поліному, що являється результуючою поточною сумою цього блоку. Якщо немає співпадіння ак*b1Å P(i-1)к зі значенням коефіцієнта розширення ("0"), то віднімання не виконується, та сума a(x ) * bi Å Pn -1(x ) передається на вихід блоку. Перша група елементів И 14 застосовується для порівняння коефіцієнта розширення зі знаком ак*b1Å P(i-1)к, а друга 16 - для управління відніманням, а (n-3) - входовий елемент АБО 15 призначений для мултиплексування коефіцієнтів розширення. Блок 6 сумування, який складається з (n-1) суматорів по модулю два, призначений для формування коефіцієнтів результуючого добутку, a(x ) * bi Å Pn -1(x ) які визначаються як сума . Множення елементів скінченних полів GF(2n) виконується як множення багаточленів та призводить до обчислення суми часткових добутків с приведенням їх по модулю утворюючого поліному. Таким чином, ефективність запропонованого пристрою визначається його багатофункціональними можливостями (діапазон степені розширення полю), регулярністю структури та можливістю реалізації у вигляді ВІС або ПЛІС. Джерела інформації: 1. Патент Російської Федерації №2058040, кл. G 06 F 7/49, 1996. 2. Патент України №4046, кл. G 06 F 7/49, 1994. 7 43629 8 9 43629 10 11 Комп’ютерна верстка Д. Шеверун 43629 Підписне 12 Тираж 28 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601