Спосіб моделювання структури додекагональних квазікристалів
Номер патенту: 80699
Опубліковано: 10.06.2013
Автори: Смоляков Олександр Васильович, Гіржон Василь Васильович, Гайворонський Ігор Володимирович
Формула / Реферат
Спосіб моделювання структури додекагональних квазікристалів, що включає вибір базисної модельної групи та її подальше розмноження, який відрізняється тим, що як модельну групу використовують правильний дванадцятикутник, а розмноження модельної групи здійснюють за формулою:
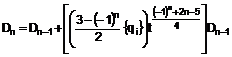 ,
,
де:
![]() - модельна група, безрозмірна величина;
- модельна група, безрозмірна величина;
![]() - номер модельної групи, безрозмірна величина;
- номер модельної групи, безрозмірна величина;
![]() - вектор базису оберненої ґратки, безрозмірна величина;
- вектор базису оберненої ґратки, безрозмірна величина;
![]() - порядковий номер базисного вектора;
- порядковий номер базисного вектора;
![]() - постійний ірраціональний коефіцієнт зміщення, що дорівнює
- постійний ірраціональний коефіцієнт зміщення, що дорівнює ![]() , безрозмірна величина.
, безрозмірна величина.
Текст
Реферат: Спосіб моделювання структури додекагональних квазікристалів включає вибір базисної модельної групи та її подальше розмноження. Як модельну групу використовують правильний дванадцятикутник. UA 80699 U (54) СПОСІБ МОДЕЛЮВАННЯ СТРУКТУРИ ДОДЕКАГОНАЛЬНИХ КВАЗІКРИСТАЛІВ UA 80699 U UA 80699 U 5 10 15 20 Корисна модель належить до фізики твердого тіла, а саме до моделювання квазікристалічних фаз з віссю симетрії 12 порядку. Відомий спосіб моделювання структури квазікристалів за допомогою проекційного методу [Ю.Х. Векилов, М.А. Черников. Квазикристаллы // Успехи физических наук. - 2012. - Т. 180. - № 6. - С. 561-586], який включає проектування на фізичний простір періодичних кристалічних ґраток більш високої розмірності. Ці ґратки повертають на деякий ірраціональний кут відносно вибраного фізичного простору, а їхні вузли проектують на нього і таким чином отримують модель структури квазікристалів. Область проектування на фізичний простір містить обмежену кількість вузлів кристалічної ґратки. Недоліками способу є використання гіпотетичних періодичних ґраток, розмірність яких перевищує три. Спільними ознаками з рішенням, що заявляється, є отримання експериментально доведених ідентичних обернених ґраток. Відомий спосіб моделювання оберненої ґратки для квазікристалів з віссю симетрії 10 порядку [V.V. Girzhon, V.M. Kovalyova, O.V. Smolyakov, M.I. Zakharenko. Modelling of decagonal quasicrystals // The Journal of Non-Crystalline Solids. - 2012. - Vol. 358. - N 2. - pp. 137-144], що включає вибір модельної групи декагональної ґратки, яка визначає базисні вектори оберненої ґратки декагонального квазікристалу, що є вершинами правильного десятикутника та їх подальше розмноження за формулою: Dn Dn 1 n 2 qi Dn 1 , (1) де: D - модельна група, безрозмірна величина; n - номер модельної групи, безрозмірна величина; - постійний ірраціональний коефіцієнт зміщення, що дорівнює 1 5 / 2 , безрозмірна величина; q - вектор базису оберненої ґратки, безрозмірна величина; 25 30 35 40 45 50 i - порядковий номер базисного вектора. Недоліками цього способу є неможливість його використання для моделювання оберненої ґратки квазікристалів з віссю симетрії, відмінною від осі 10-го порядку. Спільною з найближчим аналогом ознакою є вибір базисної модельної групи та її подальше розмноження. В основу корисної моделі поставлено задачу розробити спосіб моделювання структури додекагональних квазікристалів, який шляхом вибору групи модельної групи та її розмноження за заданим алгоритмом дозволяє побудувати двовимірну візуальну модель оберненої ґратки квазікристалів з віссю симетрії 12 порядку. Суттєвими ознаками способу є: - вибір вихідної модельної групи правильного дванадцятикутника; - розмноження вибраної модельної групи вузлів за формулою: n 1 2n 5 3 1n qi t 4 Dn 1 , (2) Dn Dn 1 2 де: D - модельна група, безрозмірна величина; n - номер модельної групи, безрозмірна величина; q - вектор базису оберненої ґратки, безрозмірна величина; i - порядковий номер базисного вектора; t - постійний ірраціональний коефіцієнт зміщення, що дорівнює 2 3 , безрозмірна величина. Відмінними від найближчого аналога ознаками є: - використання як модельної групи правильного дванадцятикутника; - розмноження вибраної модельної групи вузлів за формулою 2. На фіг. 1 зображено модельну групу D6 додекагональної квазігратки. На фіг. 2 зображено електронограму від додекагонального квазікристалу системи Та-Те. На фіг. 3 зображено накладання модельної групи D6 на експериментальну електронограму від додекагонального квазікристалу, що наведена на фіг. 2. Спосіб здійснюють таким чином: 1 UA 80699 U 5 Спочатку вибирають модельну групу, яка відповідає правильному дванадцятикутнику, позначену як група D1, та проводять 12 базисних векторів до його вершин. Потім будують групу D2 шляхом розміщення модельної групи D 1 у кожній вершині дванадцятикутника, тобто при зміщенні на базисні вектори. На наступному етапі будують групу D 3 додаванням до групи D2 дванадцяти ідентичних модельних груп, які зміщені на подвоєні значення базисних векторів. Наступну групу D4 отримують шляхом додавання до групи D3 12 ідентичних модельних груп, зміщених на базисні вектори qi , що збільшені у 2 3 раз. Алгоритм побудови групи D5 є аналогічним до побудови попередніх груп, але зміщення точок виконують на базисні вектори, 10 15 20 25 30 збільшені у 2 2 3 разів. Алгоритм побудови оберненої додекагональної ґратки можна записати у вигляді: D2 D1 qi D1,D3 D2 2qi D2 ,D4 D3 tqi D3 ,D5 D4 2tqi D4 , D 6 D 5 t 2 qi D 5 ,D 7 D 6 2t 2 qi D 6 ,D 8 D 7 t 3 qi D 7 ..., (3) де: D - модельна група, безрозмірна величина; n - номер модельної групи, безрозмірна величина; q - вектор базису оберненої ґратки, безрозмірна величина; i - порядковий номер базисного вектора; t - постійний ірраціональний коефіцієнт зміщення, що дорівнює 2 3 , безрозмірна величина. Нормування отриманої оберненої ґратки та порівняння з реальними електронограмами свідчать про адекватність вибраного способу моделювання. Приклад конкретного виконання: Запропонований спосіб було використано для моделювання оберненої ґратки квазікристалічних додекагональних фаз на прикладі сплаву системи Та-Те. Спосіб здійснювали таким чином: спочатку вибирали модельну групу, яка відповідала правильному дванадцятикутнику, позначену як група D1, та проводили 12 базисних векторів до його вершин. Потім будували групу D2 шляхом розміщення модельної групи D 1 у кожній вершині дванадцятикутника, тобто зміщення на базисні вектори. На наступному етапі будували групу D 3 шляхом додавання до групи D2 дванадцяти ідентичних модельних груп, які були зміщені на подвоєні значення базисних векторів. Наступну групу D 4 отримували шляхом додавання до групи D3 12 ідентичних модельних груп, зміщених на базисні вектори q i , що були збільшені у 2 3 раз. Алгоритм побудови групи D5 є аналогічним до побудови попередніх груп, але 35 40 45 зміщення точок виконували на базисні вектори, збільшені у 2 2 3 разів. Модель оберненої ґратки кристалу характеризує дифракційну картину, обумовлену типом симетрії досліджуваних фаз. Картина дифракції електронів при дослідженнях кристалів певного хімічного складу характеризує симетрію даної кристалічної ґратки. Побудована модельна група D6, яку наведено на фіг. 1, моделювала обернену ґратку додекагонального квазікристалу без генерації "зайвих" та малоінтенсивних відбиттів, які не спостерігаються на відповідній їй електронограмі, що наведено на фіг. 2. Ця електронограма являє собою картину дифракції електронів вздовж осі 12-го порядку від додекагонального квазікристалу системи Та-Те [М. Conrad, F. Krumeich, В. Harbrecht. A dodecagonal quasicrystalline chalcogenide // Angewandte chemie. - 1998. - Vol. 37. - N 10. - pp. 1383-1386]. Порівняння модельної групи D6 з електронограмою від додекагонального квазікристалу дало можливість підтвердити коректність запропонованого способу моделювання. Даний спосіб моделювання дозволяє побудувати реальну обернену ґратку додекагональних квазікристалів без зайвих вузлів та пустот. Запропонований спосіб дозволяє отримувати модель оберненої ґратки додекагональних квазікристалів, яка може бути використана для ідентифікації квазікристалічних додекагональних фаз при їх дифрактометричних дослідженнях. 50 ФОРМУЛА КОРИСНОЇ МОДЕЛІ 55 Спосіб моделювання структури додекагональних квазікристалів, що включає вибір базисної модельної групи та її подальше розмноження, який відрізняється тим, що як модельну групу використовують правильний дванадцятикутник, а розмноження модельної групи здійснюють за формулою: 2 UA 80699 U 5 1n 2n 5 3 1n q i t 4 Dn 1 , Dn Dn 1 2 де: D - модельна група, безрозмірна величина; n - номер модельної групи, безрозмірна величина; q - вектор базису оберненої ґратки, безрозмірна величина; i - порядковий номер базисного вектора; t - постійний ірраціональний коефіцієнт зміщення, що дорівнює 2 3 , безрозмірна величина. 3 UA 80699 U Комп’ютерна верстка В. Мацело Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for the simulation of dodecagonal quasi-crystal structure
Автори англійськоюHirzhon Vasyl Vasyliovych, Smoliakov Oleksandr Vasyliovych, Haivoronskyi Ihor Volodymyrovych
Назва патенту російськоюСпособ моделирования структуры додекагональных квазикристаллов
Автори російськоюГиржон Василий Васильевич, Смоляков Александр Васильевич, Гайворонский Игорь Владимирович
МПК / Мітки
МПК: G09B 23/06, G09B 23/26
Мітки: додекагональних, квазікристалів, спосіб, моделювання, структури
Код посилання
<a href="https://ua.patents.su/6-80699-sposib-modelyuvannya-strukturi-dodekagonalnikh-kvazikristaliv.html" target="_blank" rel="follow" title="База патентів України">Спосіб моделювання структури додекагональних квазікристалів</a>
Попередній патент: Теплоакумулюючий матеріал
Наступний патент: Спосіб попередження резорбції альвеолярного відростка щелеп у хворих на генералізований пародонтит
Випадковий патент: Потужний нвч напівпровідниковий помножувач частоти










