Спосіб створення моделі керованого процесу на основі керувального впливу

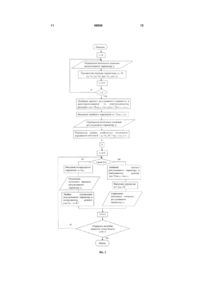
1. Спосіб створення моделі керованого процесу на основі керувального впливу в системах автоматичного керування з неповною апріорною інформацією про керований процес, поведінку керованих об'єктів під дією зовнішніх збурень і керувальних впливів в яких описують лінійними операторами, який відрізняється тим, що інформацію про керований процес активно накопичують в процесі керування, для чого створюють в реальному часі модель керованого процесу у вигляді керувального впливу, еквівалентного за своєю дією на керований об'єкт дії зовнішніх збурень, для чого вводять таке керування, яким подвоюють значення вихідної змінної порівняно з некерованим процесом. 3 гію у вигляді оптимального розподілу щільності ймовірностей керувального сигналу. Недоліками цього способу зокрема є: - необхідність апріорних формальних математичних моделей об'єкта керування та зовнішнього збурення, а також знання апріорних розподілів їх параметрів та характеристик для розрахунку апостеріорних розподілів; - неможливість створення моделі керованого процесу в реальному часі через необхідність накопичення статистичних даних про реакцію керованого об'єкта на "вивчальну" складову керувального впливу для забезпечення необхідних точності та вірогідності створеної моделі. Вказані недоліки не дозволяють керувати об'єктом без наявності формальної математичної моделі його поведінки при дії керувальних впливів та зовнішніх збурень, виконувати швидку адаптацію керувального пристрою до процесу керування, здійснювати керування при повній відсутності апріорної інформації про керований процес. Вказаний спосіб приймається як аналог. У відомих системах регулювання вихідних величин об'єктів керування здійснюють способами, основаними на фундаментальних принципах [Тихонов А.И. Введение в теорию автоматического управления. Курс лекций. 2002., Лекция 1.: www.toehelp.ru]: - розімкнутого керування; - компенсації; - зворотного зв'язку. Всі вказані принципи вимагають наявності формальної математичної моделі керованого процесу (об'єкта керування та зовнішнього збурення) для синтезу керувального впливу. Структура та параметри такої моделі можуть бути апріорі невідомими чи змінюватись в процесі керування. Для уточнення апріорної моделі керованого процесу застосовують різноманітні способи її ідентифікації (в тому числі і в процесі керування), а для відповідного корегування параметрів керувального пристрою в процесі керування - різноманітні способи його адаптації. Відомий спосіб синтезу оптимального керування в процесі керування в реальному часі з використанням прогнозу некерованого руху [Справочник по теории автоматического управления. /Под. ред. А.А. Красовского. - М: Наука. Гл. ред. физ.мат. лит., 1987. - С.428]. Спосіб включає наступні операції: - Вимірюють чи оцінюють поточний стан об'єкта в дискретні моменти часу, які відповідають початку чергового циклу формування керування; - Використовуючи математичну модель об'єкта керування, прогнозують некерований (вільний) рух об'єкта на заданому інтервалі [tu,t2] оптимізації керування (інтервал прогнозування) з початковими умовами, які збігаються з поточним на момент tu станом об'єкта чи знаходяться в деякому околі цього стану; - Обчислюють градієнт зміни функції V(x,t) поточного стану об'єкта, яка входить до критерію якості керування; - Формують сигнал керування за умовою мінімізації прийнятого критерію якості керування. 49959 4 Недоліками цього способу зокрема є: - Необхідність створення формальної математичної моделі керованого процесу для прогнозування некерованого процесу; - Неможливість прогнозування керованого процесу в цілому через відсутність інформації про конкретну реалізацію зовнішнього збурення, яка діє в даний момент. Вказані недоліки не дозволяють регулювати вихідну змінну керованого об'єкта за відсутності формальної математичної моделі керованого процесу чи її зміні в процесі керування. Вказаний спосіб приймається як аналог. У відомих системах параметричну ідентифікацію математичної моделі об'єкта керування в процесі його функціонування при дії невідомих зовнішніх збурень на основі даних про вхідні і вихідні змінні здійснюють зокрема способом, основаним на пошукові екстремуму цільового функціоналу нев'язки параметрів об'єкта та його моделі в просторі параметрів моделі, зокрема, шляхом використання спеціальних тестових сигналів, які додають до вхідного сигналу. Тестові сигнали вибирають серед періодичних чи випадкових функцій з нульовим середнім значенням таким чином, щоб спектр частот тестового сигналу знаходився в області частот, які значно перевищують верхню межу спектру вхідного сигналу. Шляхом синхронного детектування реакції об'єкта на тестовий сигнал знаходять градієнт екстремуму цільового функціоналу нев'язки [Справочник по теории автоматического управления. / Под. ред. А.А. Красовского. - М.: Наука. Гл. ред. физ.-мат. лит., 1987. - С.276-278]. Недоліками цього способу зокрема є: - необхідність використання спеціальних тестових сигналів, непотрібних в процесі нормального функціонування об'єкта керування; - необхідність врахування впливу на отримані дані, на основі яких виконують ідентифікацію, невідомих зовнішніх збурень. Вказані недоліки не дозволяють ідентифікувати параметри математичної моделі об'єкта керування в процесі його нормального функціонування в умовах сильних випадкових збурень з невідомими статистичними характеристиками. Вказаний спосіб приймається як аналог. Технічною задачею, на вирішення якої спрямована корисна модель, є створення керувальним пристроєм в процесі керування в реальному часі необхідної для здійснення керування моделі керованого процесу за відсутності апріорної інформації про нього. Суть запропонованого способу полягає в тому, що модель керованого процесу створюють у вигляді керувального впливу, еквівалентного за своєю дією на керований об'єкт дії зовнішніх збурень на інтервалі часу створення моделі шляхом копіювання некерованого процесу. Спосіб відрізняється тим, що: - об'єкт керування і зовнішнє збурення, що діє на нього, моделюють в реальному часі як єдине ціле - керований процес; - модель є не стохастичною, а детермінованою; - модель створюють не у вигляді оператора, 5 який описує поведінку об'єкта під дією збурень, та даних, які описують розподіл ймовірностей значень збурення, а у вигляді регресійної залежності значень керувального впливу від часу. Технічним результатом застосування корисної моделі є забезпечення можливості керування об'єктом в умовах апріорної невизначеності за відсутності формальних математичних моделей об'єкта керування та збурення. Технічною задачею, на вирішення якої також спрямована корисна модель є створення регулятора, здатного зменшувати відхилення регульованої змінної від заданого значення без використання формальної математичної моделі керованого процесу (об'єкта керування та зовнішнього збурення). Суть запропонованого способу полягає в тому, що процес регулювання складається з таких основних етапів, які, при необхідності, повторюють: - Моделюють керований процес керувальним впливом; - Програмують керувальний вплив на основі отриманої моделі керованого процесу; - Здійснюють запрограмоване керування. Спосіб також відрізняється від відомого тим, що використовують неформальну модель керованого процесу в цілому у вигляді керувального впливу еквівалентного дії конкретного зовнішнього збурення на конкретний керований об'єкт на часовому інтервалі моделювання, яку створюють в процесі керування в міру її необхідності. Технічним результатом застосування корисної моделі є зменшення величини відхилення об'єкта від заданого положення під впливом збурень з використанням даних про регульований параметр і керувальний вплив при відсутності формального опису керованого процесу та апріорної інформації про нього. Технічною задачею на вирішення якої спрямована корисна модель є також параметрична ідентифікація математичної моделі об'єкта керування в процесі його функціонування при дії невідомих зовнішніх збурень з використанням відомих значень керувального впливу та спостережених значень регульованої змінної і без використання спеціальних тестових впливів. Суть запропонованого способу полягає в тому, що, у випадку використання описаного вище способу регулювання вихідної змінної на часових інтервалах створення моделі керованого процесу на основі керувального впливу, є відомим керувальний вплив еквівалентний дії збурення та може бути виміряна подвоєна реакція об'єкта на нього, що дозволяє ідентифікувати параметри математичної моделі на основі знання вхідного і вихідного сигналів. Спосіб відрізняється від відомих способів тим, що для його реалізації використовують модель керованого процесу у вигляді даних про керувальний вплив, еквівалентний за своєю дією на об'єкт дії зовнішніх збурень. Технічним результатом застосування корисної моделі є забезпечення можливості виконання параметричної ідентифікації математичної моделі об'єкта керування в процесі його нормальногофу 49959 6 нкціонування без використання спеціальних тестових впливів та усунення впливу на результат ідентифікації невідомих зовнішніх збурень. Запропонований спосіб ілюстрований фігурами 1-5: На Фіг.1. зображено структурно-функціональну схему системи керування, в якій може бути застосована корисна модель, де: x(t) - невідоме зовнішнє збурення; u(t) - керувальний вплив; y(t) - регульований параметр; А - невідомий, але лінійний оператор, який визначає реакцію об'єкта на зовнішнє збурення; В - невідомий, але лінійний оператор, який визначає реакцію об'єкта на керувальний вплив; Bu(t) - реакція об'єкта на керувальний вплив; Ax(t) - реакція об'єкта на зовнішнє збурення. На Фіг.2 зображено алгоритм створення обчислювальним пристроєм регулятора моделі керованого процесу на основі керувального впливу для випадку коли А=В=К (збурення і керування приведені до одного входу), шумами спостереження регульованого параметру та керувального впливу можна знехтувати, задане значення регульованого параметру дорівнює нулю. Обчислення виконують в дискретні моменти часу ti=i∆t, де і - номер відліку, ∆t - інтервал дискретизації. В обчисленнях використовують лише відомі регулятору значення власного керувального впливу ui та доступні для спостереження значення регульованого параметру уi, причому: yuі - спостережене значення регульованого параметру в некерованому режимі в момент ti; усі - спостережене значення регульованого параметру в керованому режимі в момент ti; yupi - прогнозоване чи відновлене шляхом обчислень значення регульованого параметру в некерованому режимі в момент ti; усрі - прогнозоване значення регульованого параметру в керованому режимі в момент ti; К* - оцінка коефіцієнта підсилення об'єкта, N - необхідна кількість точок моделі. На Фіг.3 зображено процеси в системі керування і зокрема модель керованого процесу на основі керувального впливу, створену обчислювальним пристроєм за алгоритмом, зображеним на Фіг.2, якщо сигнал збурення x(t)=c·sin( t+ ) є реалізацією випадкового процесу X(t)=Csin( t+ ), де С, , - випадкові величини, конкретні параметри керованого процесу дорівнюють К=3, с=2, = , =0,1, і: 1 - невідоме зовнішнє збурення; 2 - відхилення регульованого параметру від заданого значення під дією зовнішнього збурення (частково спостережений, частково прогнозований і відновлений некерований процес); 3 - керувальний вплив (модель керованого процесу); 4 - регульований параметр (керований процес). 5 - перша точка моделі. Параметри керованого процесу К, с, , алгоритмові створення моделі невідомі (в обчисленнях їх не використовують). 7 На Фіг.4. зображено алгоритм регулювання. Обчислення виконують в дискретні моменти часу ti=i∆t, де і - номер відліку, ∆t - інтервал дискретизації. В обчисленнях використовують лише відомі регулятору значення власного керувального впливу ui та доступні для спостереження значення регульованого параметру уі u*(t) - регресійна залежність керувального впливу від часу, отримана в результаті роботи алгоритму моделювання (Фіг.2). На Фіг.5 зображені процеси в системі керування, отримані при застосуванні алгоритму, зображеного на Фіг.4, якщо об'єкт керування - підсилювальна ланка з коефіцієнтом підсилення К=3, сигнал збурення x(t)=c1·sin( 1t+ 1)+c2·sin( 2t+ + 2)+ (t), де c1=2, 1=0,3 1/с, 1=- /12, с2=0,25, 2=2 1/с, 2=0, (t) - рівномірний білий шум з інтенсивністю 2=0,0003 з відліками через ∆t=0,01c, інтерпольований кубічними сплайнами. Процедура накопичення інформації в процесі синтезу моделі керованого процесу -ARIMA(0,2,2) з ваговими коефіцієнтами 1=0,1, 2=-0,2. Параметри керованого процесу К, c1, 1 1 с2, 2, 2 алгоритмові регулювання невідомі (в обчисленнях їх не використовують): 1 - невідоме зовнішнє збурення; 2 - відхилення регульованого параметру від заданого значення під дією зовнішнього збурення (некерований процес); 3 - керувальний вплив; 4 - регульований параметр (керований процес). Спосіб створення моделі керованого процесу на основі керувального впливу здійснюють наступним чином. 1. Протягом деякого часу Т0-Т1 отримують значення регульованого параметру при нульовому значенні керувального впливу u(t)=0 під дією лише зовнішнього збурення з метою прогнозування поведінки некерованого об'єкта yu(t) з заданою точністю і здійснюють вказане прогнозування загальновідомими математичними методами екстраполяції на часовий інтервал Т1-Т3, внаслідок чого отримують значення yup(t). 2. В момент часу t=T1 вводять деяке керування u(t) (наприклад, ступінчате) в бік відхилення об'єкта під дією зовнішнього збурення x(t), яке приймають за одиничне, і протягом часового інтервалу Т1-Т2, Т2