Спосіб шифрування зображення з використанням хаотичного відображення

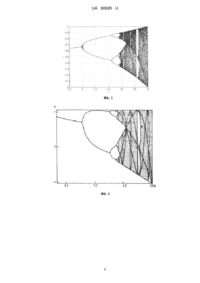
Реферат: Спосіб шифрування зображення з використанням хаотичного відображення полягає в тому, що зображення складається з сітки пікселів, які є набором трьох компонент: червона, зелена, синя, кожна з яких є початковими умовами для одномірного відображення, що використовуються для генерації ключа, генероване значення якого сумарно з перетвореним в десятковий дріб значенням кожної складової кольору утворює зашифровану складову кольору, що накладається з двома іншими зашифрованими складовими кольору, утворюючи зашифрований піксель, причому для шифрування використовують три різні одномірні відображення: логістичне, квадратичне, кубічне, кожне з яких генерує свій ключ для шифрування кожної складової кольору. UA 80695 U (54) СПОСІБ ШИФРУВАННЯ ЗОБРАЖЕННЯ З ВИКОРИСТАННЯМ ХАОТИЧНОГО ВІДОБРАЖЕННЯ UA 80695 U UA 80695 U 5 10 15 20 25 30 35 40 45 50 Корисна модель належить до області радіотехнічних пристроїв та засобів телекомунікацій, зокрема до систем захищеної передачі інформації, що використовують одномірні хаотичні відображення при шифруванні повідомлення. Відомий алгоритм шифрування інформації, що використовує псевдовипадковий генератор ключа, побудований на двох одномірних відображеннях [1]. Як хаотичні системи використовується парабола М. Фейгенбаума, тобто дві хаотичні системи мають однаковий ітеративний принцип з різними початковими умовами. Перша система генерує випадкові числа для оновлення параметрів другої, а вихідна псевдовипадкова послідовність є результатом перемноження двох логістичних хаотичних систем. В загальному алгоритм шифрування та дешифрування виглядає наступним чином: зображення перетворюється в потік бінарних даних, на нього накладається псевдовипадкова ключова послідовність та утворюється зашифроване зображення. Одним із недоліків такого способу є використання двох динамічних систем з однаковим ітеративним принципом. Такий алгоритм характеризується невисокою криптографічною стійкістю, що оцінюється по коефіцієнту кореляції двох сусідніх пікселів. Також відомий алгоритм шифрування та дешифрування зображення з хаотичними відображенням сіток [2], що є найбільш близьким до запропонованого способу шифрування зображення, та використовує логістичне відображення для шифрування зображення. Ідеєю алгоритму є те, що будь-яке зображення може бути представлене в вигляді сітки пікселів, кожен з яких має окремий колір. Колір пікселя це комбінація трьох компонент: червона, синя, зелена. Внаслідок цього створюється три паралельні хаотичні відображення сітки, перетворюючи кожен з цих трьох компонент кольору в відповідне значення змінних відображення, та використовуючи ці значення як початкові умови для логістичного відображення. Логістичне відображення в алгоритмі використовується як генератор ключа. Три компоненти кольору шифруються окремо за допомогою логістичного відображення. Такий алгоритм характеризується досить високою криптостійкістю, але недоліком його є те, що після проведення шифрування зображення контури оригінального зображення все ще можна розгледіти. Задачею корисної моделі є підвищення криптостійкості алгоритму шифрування зображення. Суть корисної моделі полягає в тому, що для підвищення криптостійкості інформації, при передаванні чи збереженні зображення, застосовуються три одномірних відображення (логістичне квадратичне та кубічне), розкладаючи кожен піксель на три складові (червону зелену та синю), перетворюючи їх градацію від 0 до 255 в десятковий дріб в межах від 0 до 1, далі отримане значення кожної складової використовується в якості початкових умов для кожного з відображень. Зображення шифрується, задавши відповідні параметри для кожного з відображень, кількість ітерацій та кількість циклів. Новим є те, що шифрування здійснюється, розкладаючи кожен піксель на три складові і шифруючи кожну з них окремим відображенням. Проітерувавши задану кількість разів та повторивши вказану кількість циклів з кожною складовою отримаємо зашифроване значення для кожної складової, перетворивши отримані значення в градацію кольору, накладаємо три складові та отримаємо зашифроване зображення. На фіг. 1 приведена структурна схема способу шифрування зображення. На фіг. 2 приведено розбиття зображення на пікселі. На фіг. З приведено біфуркаційну діаграми логістичного відображення. На фіг. 4 приведено біфуркаційну діаграми квадратичного відображення. На фіг. 5 приведено біфуркаційну діаграму кубічного відображення. На фіг. 6 приведена сітка пікселів однієї зашифрованої складової кольору. Система, що ілюструє суть найближчого до пропонованого способу шифрування, працює наступним чином [2]. Розбиваючи зображення на пікселі та кожен піксель на три складові кольору, отримуються початкові умови для логістичного відображення (1). Ітеруючи логістичне відображення певну кількість разів та проводячи певну кількість циклів, здійснюється шифрування зображення, починаючи з першого пікселя до останнього. xn1  rxn (1 xn ) 55 (1) Дешифрування зображення здійснюється, використовуючи ту саму кількість ітерацій та циклів в зворотному напрямку. Для дешифрування останнього пікселя використовується зашифроване значення передостаннього і т.д. Структурна схема вдосконаленого способу шифрування зображення приведена на фіг. 1 та складається з наступних елементів: 1 UA 80695 U 5 10 15 1 - Вхідне зображення; 2 - Визначення кількості пікселів; 3 - Розбиття пікселів на три складові; 4 Червона складова; 5 - Синя складова; 6 - Зелена складова; 7 - Визначення значення C та x c кожного пікселя; 8 - Визначення початкової умови для шифрування першого пікселя; 9 - Ітерування n разів одномірного рівняння та отримання значення x n ; 10 - Шифрування першого пікселя; 11 - Визначення початкової умови для шифрування другого пікселя; 12 - Шифрування кожного пікселя червоної складової; 13 - Вихідне зашифроване зображення. Працює наступним чином. Зображення розбивається на пік селі, утворюючи сітку пікселів, кожен з яких має окремий колір. Колір кожного пікселя є комбінацією трьох компонент: червона, C  (Cr , Cg,Db зелена, синя кожна з яких приймає ціле значення в межах 0255. Таким чином, отримується три паралельні хаотичні відображення сітки. Перетворюючи кожну з цих трьох g x C  (xr , x C , x b , C C змінних відображення, використовуємо ці значення як початкові умови x C  x 0 для трьох різних одномірних відображень: логістичне (1), квадратичне (2) та кубічне (3), біфуркаційні діаграми яких приведені на фіг. 3, 4 та 5. компонент 20 кольору в відповідне значення 2 x n 1  1  x n 3 x n 1    bx n  x n 25 (2) (3) Шифрування червоної складової відбувається з використанням логістичного відображення. Для цього вибираємо значення параметру   3.9 . Для цього параметру хаотичний атрактор логістичного відображення займає фазовий простір між xmin  0.09062 та xmax  0,975 . Далі перетворюємо червону компоненту кольору C кожного пікселя в змінну x c відповідного відображення в сітці, дане перетворення здійснюється за допомогою наступної формули: x C  xmin  x(C / 255) (4) 30 35 де x  x max  x min . та для значення   3.9 складає 0,88438. Спосіб шифрування включає наступні кроки. , 1. Зображення складається з N  M  m пікселів (i  12,...,m) , як показано на фіг. 2. Кожен піксель розбивається на три компоненти кольору і-го пікселя перетворюються в три значення змінної x C згідно рівняння (4). m 2. Значення кольору x C останнього пікселя m використовується як початкова умова для 1 m шифрування першого пікселя (i=1), тобто, x 0  x C . 1 3. Після n ітерацій першого відображення, ми отримаємо змінну відображення x n та 40 1 додаємо до нього значення кольору пікселя x C і отримуємо зашифроване значення першого пікселя. Сумарне значення використовуються як початкова умови для наступного відображення, 2 1 1 тобто, x 0  x n  x C . 4. Ітеруємо всі відображення послідовно стартуючи з першого відображення і таким чином i i шифруємо всі пікселі зображення. Крім того, якщо сума x n  x C  x max віднімаємо x , тобто, 45  x i0 1  x in  x iC  x . Після одного циклу, що починається з першого відображення до останнього, ми отримаємо відображення сітки, що приведене на фіг. 4. Воно може бути візуалізоване 2 UA 80695 U i i перетворенням нової змінної відображення x n  x C до відповідного значення кольорів, згідно рівняння (5). C  roundxn  xmin 255 / x 5 (5) 5. Повторюємо кроки 3 та 4 і здійснюємо кілька циклів. Для наступного циклу, нове значення m m m кольору останнього відображення x C  j  x n  j  x C  j ( j - номер циклу) використовуються як початкова умова для першого відображення щоб запустити наступний цикл, тобто, 10 15 x1 j  1  x m j . Після j циклів, ми отримаємо відображення сітки ідентичне до того, що 0 C показано на фіг 4 та можемо візуалізувати зашифроване зображення використовуючи рівняння (5). 6. Повторюємо всі кроки для трьох компонент кольору (червона, зелена, синя). Накладаємо три складові одна на одну та отримуємо зашифроване зображення. Для дешифрування, необхідно відтворити оригінальний цикл зображення в зворотному напрямку, стартуючи з останнього відображення m , та ідучи до першого відображення (i  1) здійснюючи ту саму кількість ітерацій для кожного відображення як і при шифруванні. Алгоритм дешифрування способу шифрування зображення включає наступні кроки: 1. Спочатку необхідно відновити зображення циклу j  1 , починаючи з останнього відображення. Зашифроване значення передостаннього відображення в j циклі, це початкова m m 1 умова для останнього відображення в циклі j  1 , тобто, x 0 j  1  x C j . Починаючи з цих 20 m початкових умов, ітеруємо останнє відображення n разів і отримаємо значення x n j  1 . m m Віднімаючи ці значення від значення кольору останнього відображення в; циклі, x C j  xn ( j  1) , 25 m отримаємо значення кольору останнього відображення в j  1 циклі, тобто, x c ( j  1) . 2. Потім беручи зашифроване значення відображення m 2 як початкову умову для відображення m 1, знаходимо значення кольору останнього відображення в циклі j  1 і т. д. 3. Повторюємо крок 2 для кожного відображення в зворотному напрямку з останнього відображення до першого відображення та відтворюємо зображення циклу j  1 . j  1 в циклі j  1 використовуємо розшифроване значення кольору останнього відображення m j  1 циклі, 4. Для відновлення значення кольору першого відображення 30 x m j  1 , як початкову умову для першого відображення. Ітеруємо необхідну кількість разів та C віднімаємо від зашифрованого значення першого пікселя. i 5. Повторюємо всі попередні кроки j разів та отримаємо відображення сітки x C (0) , що 35 40 i конвертується рівнянням (5) в значення кольорів C . 6. Повторюємо всі кроки для кожної компоненти кольору та накладаючи три зображення отримаємо оригінальне зображення. Шифрування та дешифрування інших двох складових відбувається аналогічним чином. Джерела інформації: 1. Liu S., Sun J., Xu Zn. An improved image encryption algorithm based on chaotic system/ S. Liu, J. Sun, Zn. Xu// Journal of computers.-2009. -Vol. 4-№ 11-Pp. 1091-1100. 2. Pisarchik A.N., Flores-Carmona N.J. and Carpio-Valadez M. Encryption and decryption of images with chaotic map lattices/ A.N. Pisarchik, N.J. Flores-Carmona and M. Carpio-Valadez // CHAOS 16,033118 (2006) 6 P. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 45 Спосіб шифрування зображення з використанням хаотичного відображення, який полягає в тому, що зображення складається з сітки пікселів, які є набором трьох компонент: червона, зелена, синя, кожна з яких є початковими умовами для одномірного відображення, що використовуються для генерації ключа, генероване значення якого сумарно з перетвореним в 3 UA 80695 U 5 десятковий дріб значенням кожної складової кольору утворює зашифровану складову кольору, що накладається з двома іншими зашифрованими складовими кольору, утворюючи зашифрований піксель, який відрізняється тим, що для шифрування використовують три різні одномірні відображення: логістичне, квадратичне, кубічне, кожне з яких генерує свій ключ для шифрування кожної складової кольору. 4 UA 80695 U 5 UA 80695 U Комп’ютерна верстка І. Мироненко Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 6