Пристрій багатошарової двонаправленої асоціативної пам’яті

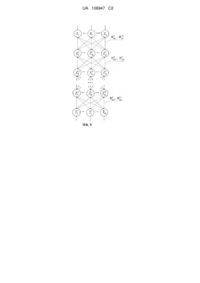
Реферат: Пристрій багатошарової двонаправленої асоціативної пам'яті належить до обчислювальної техніки та може бути використаний при побудові баз знань технологічних процесів та систем підтримки прийняття рішень. Пристрій може зберігати та відновлювати зі своєї пам'яті ланцюги асоціацій завдяки тому, що в структуру мережі введення N шарів нейронів, які послідовно з'єднані один з одним парами двонаправлених зважених зв'язків, при цьому кожен нейрон першого з N шарів нейронів з'єднується двонаправленими зваженими зв'язками з кожним нейроном першого сенсорного шару, а кожен нейрон останнього з N шарів нейронів з'єднаний двонаправленими зваженими зв'язками з кожним нейроном другого сенсорного шару нейронів. Технічним результатом є зберігання та відновлювання зі своєї пам'яті асоціативні зображення та будування ланцюгів асоціацій. UA 108947 C2 (12) UA 108947 C2 UA 108947 C2 5 10 15 20 25 30 35 40 45 50 55 60 Винахід належить до обчислювальної техніки, зокрема до області побудови автоматизованих систем керування складними технічними об'єктами. Винахід може бути використаний при побудові баз знань технологічних процесів та систем підтримки прийняття рішень. Відомий пристрій гібридної ієрархічної нейронної мережі для зберігання знань технологічного процесу механообробки, що складається з восьми модулів, перші три являють собою нейронні мережі адаптивної резонансної теорії (АРТ-1У), які по призначенню ширини, довжини та висоти виробу проводять аналіз розмірів та конфігурації майбутнього виробу, результати роботи подаються на вхід четвертого модуля (НМ АРТ-1), де визначається вигляд заготовки, п'ятий модуль являє собою нейронну мережу АРТ-1s, що по типу поверхні та виду операції визначає типи станків, які можуть виконати дану операцію, шостий модуль є дискретною нейронною мережею APT-1h, де по габаритах заготовки і типам станків визначається підмножина станків, які підходять для обробки поверхні виробу з заданими габаритними розмірами, сьомий модуль - дискретна нейронна мережа АРТ-1s, він визначає підмножину станків, що забезпечують задану точність обробки, восьмий модуль являє собою нейронну мережу Хеммінга яка визначає станок, що забезпечує мінімальну вартість операції [1]. Недоліком розглянутого пристрою є те, що він не здатен зберігати та відновлювати зі своєї пам'яті двонаправлені асоціативні зображення. Відомий пристрій двонаправленої асоціативної пам'яті, що складається з двох сенсорних шарів нейронів та двох керуючих нейронів, що зв'язані вихідними зв'язками з керуючими нейронами відповідних модулів та вхідними зв'язками з усіма нейронами в проміжному шарі, елементи якого зв'язані парами двонаправлених зважених зв'язків з відповідними їм елементами розпізнавальних шарів двох однотипних паралельно працюючих модулів, кожний з яких являє собою дискретну нейронну мережу адаптивної резонансної теорії, що містить у собі шари інтерфейсних елементів, нейрони яких пов'язані з відповідними їм елементами сенсорних шарів парами бінарних двонаправлених зв'язків, шари розпізнавальних елементів, нейрони яких пов'язані з кожним з елементів у відповідних їм інтерфейсних шарах парами двонаправлених зважених зв'язків з безперервними ваговими коефіцієнтами, вирішуючі нейрони, які зв'язані збудливими вхідними зв'язками з усіма елементами сенсорних шарів, гальмуючими вхідними зв'язками з усіма елементами інтерфейсних шарів та збудливими вихідними зв'язками з усіма елементами розпізнавальних шарів й керуючи нейрони модулів, які зв'язані збудливими вхідними зв'язками з усіма елементами сенсорних шарів, збудливими вихідними зв'язками з усіма елементами інтерфейсних шарів та гальмуючими вхідними зв'язками з усіма елементами розпізнавальних шарів, а також зв'язані вхідними зв'язками з відповідними керуючими нейронами мережі [2]. При порівнянні з першим аналогом даний пристрій здатен здійснювати двонаправлене відновлення асоціативних зображень зі своєї пам'яті. Однак недоліком розглянутого пристрою двонаправленої асоціативної пам'яті є складність його апаратної реалізації. Найбільш близьким до заявленого пристрою є пристрій нейронної мережі, що одержала назву двонаправленої асоціативної пам'яті й складається з двох сенсорних шарів елементів, нейрони яких зв'язані між собою парами зважених двонаправлених зв'язків з відповідними ваговими коефіцієнтами [3]. При порівнянні з відомими аналогами пристрій-прототип (двонаправлена асоціативна пам'ять) має спрощену структурну реалізацію й здатен здійснювати двонаправлене відновлення асоціативних зображень (векторів) зі своєї пам'яті. Однак у розглянутого прототипу відсутня можливість отримання ланцюгів асоціацій між вхідними та вихідними зображеннями, тобто неможливе багатошарове відновлення асоціацій з пам'яті пристрою. Таким чином, недоліком прототипу є те, що він не в змозі отримати ланцюги асоціацій між вхідними та вихідними зображеннями, тобто неможливе багатошарове відновлення асоціацій з пам'яті пристрою. Задача винаходу - розробка пристрою багатошарової двонаправленої асоціативної пам'яті, що має можливістю отримання ланцюгів асоціацій між вхідними та вихідними зображеннями. Задача вирішується завдяки тому, що пристрій двонаправленої асоціативної пам'яті перебудовується шляхом введення в структуру мережі N шарів нейронів, які послідовно з'єднані один з одним парами двонаправлених зважених зв'язків, при цьому кожен нейрон першого з N шарів нейронів з'єднується двонаправленими зваженими зв'язками з кожним нейроном першого сенсорного шару, а кожен нейрон останнього з N шарів нейронів з'єднаний двонаправленими зваженими зв'язками з кожним нейроном другого сенсорного шару нейронів. У результаті додавання в структуру нейронної мережі перерахованих вище шарів нейронів досягається можливість побудови ланцюгів асоціацій між вхідними та вихідними зображеннями. 1 UA 108947 C2 5 Це стає можливим завдяки тому, що кожен нейрон кожного Z шару нейронів (фіг. 1) пов'язаний з кожним нейроном попереднього шару, що дозволяє при проходженні кожного шару отримувати нову асоціацію на основі попередньої. Винахід ілюструється кресленням (фіг. 1), на якому наведена схема пристрою багатошарової двонаправленої асоціативної пам'яті, розробленої на основі нейронних мереж двонаправленої асоціативної пам'яті. Винахід складається з двох сенсорних шарів нейронів вхідного i (i  1, n) та вихідного j ( j  1 m) , нейрон 10 , а також з N проміжних шарів вхідного шару i (i  1, n) двонаправлених зважених зв'язків з кожним нейроном 1 (q1  1 g1) , q 1 пов'язаний 1 Wiq 1, 2 Wq i 1 з , 2 (q2  1 g2 ) , q 2 кожним ,…, N (qN  1 gN ) , qN . Кожен нейроном 1 -шару парами (i  1 n; q1  1 g1) , кожен нейрон 1 -шару пов'язаний , ,  2 -шару парами двонаправлених зважених зв'язків 1 Wq q 1 2 , 2 Wq q 2 1 (q1  1 g1; q2  1 g2 ) , кожен нейрон шару  2 пов'язаний з кожним нейроном наступного шару  3 , , парами двонаправлених зважених зв'язків. По аналогії кожен наступний k -шар пов'язаний з 1 2 (k 1) (k  4, N  1) парами двонаправлених зважених зв'язків Wqk 1qk , Wqk qk 1 попереднім шаром  15 (qk 1  1 gk 1; qk  1 gk ) , а також з наступним (k 1) -шаром парами двонаправлених зважених , , 1 Wq q зв'язків k k 1 , 2 Wq q k 1 k (qk  1 gk ; qk 1  1 gk 1) . Вихідний  -шар нейронної мережі пов'язаний з , , попереднім N -шаром парами двонаправлених зважених зв'язків. Розроблена мережа функціонує відповідно до двох алгоритмів: навчання та розпізнавання. Алгоритм навчання являє собою процес визначення навчального набору зображень та 20 25  , 1 , 2 , ..., N , j qN побудови матриць вагових зв'язку між шарами нейронів: i q1 q2 . Навчання проводиться з використанням навчального набору зображень. Процес навчання реалізовується в формі обчислень, це означає, що спочатку обчислюються вагові матриці по відомих формулах. Вагові матриці для зв'язку першого сенсорного шару та першого проміжного шару розраховуються за формулами: 1 Wiq  1 2 Wq i 1  L  Si t  , i  1, n, q1  1, g1; q 1 WiqT 1 (1) , (2) S , t  де - елементи матриць зв'язків, T - символ транспонування матриці, i q1 - пари асоціативних зображень,  - номер пари асоціативних зображень, L - загальна кількість пар асоціативних зображень. f (U Для біполярних вхідних зображень функції активації p в х.р) для елементів  - і  -шарів задаються виразом: 1 Wiq , 1 30 1  1 2 Wq i 1 1, якщо Uв х. ( t )  ,  Uв их. ( t  1)  Uв их. ( t ), якщо Uв х. ( t )   , 0, якщо U ( t )  , в х.   (3) де Uв их., Uв х. - вхідні та вихідні сигнали  -гo елемента,  - поріг  -гo елемента,   1, L . Приклад навчання мережі з біполярними нейронами для запам'ятовування двох ланцюгів 35 1 1 1 1 2 2 2 2 асоціативних зображень (S , S1, S2, S3 ), (S , S1 , S2, S3 ), представлених на фіг. 2, що описуються двійковими векторами: 2 UA 108947 C2 S1  (1,1,1,1,1,1,  1,  1,  1,1,1,  1,  1,1,1,1,  1,1,1,1,1,  1,  1,  1,1,1,1,1,1,1, ), S1  ( 1,1,1,1,  1,1,  1,  1,  1,1,1,  1,  1,  1,1,1,  1,  1,  1,1,1,  1,  1,  1,1,  1,1,1,1,  1), 1 S1  ( 1,1,1,1,  1,1,  1,  1,  1,1,  1,1,1,1,  1,1,  1,  1,  1,1,1,  1,  1,  1,1,  1,1,1,1,  1, ), 2 S1  ( 1,1,1,1,  1,1,  1,  1,  1,1,  1,1,1,1,  1,1,  1,  1,  1,1,  1,1,1,1,  1,  1,  1,1,  1,  1), 3 S2  ( 1,1,1,1,  1,  1,1,1,1,  1,  1,1,1,1,  1,  1,1,1,1,  1,  1,1,1,1,  1,  1,1,1,1,  1,), 2 S1  ( 1,1,1,1,  1,  1,1,1,1,  1,1,1,1,1,1,1,1,1,1,1,  1,1,1,1,  1,  1,1,1,1,  1), S2  ( 1,1,1,1,  1,  1,1,  1,1,  1,1,  1,  1,  1,1,1,  1,  1,  1,1,  1,1,  1,1,  1,  1,1,1,1,  1), 2 5 2 S3  ( 1,  1,1,  1,  1,  1,1,  1,1,  1,1,  1,  1,  1,1,1,  1,  1,  1,1,  1,1,  1,1,  1,  1,  1,1,  1,  1). Побудова вагових матриць пристрою здійснюється за формулою (1). Побудовані вагові матриці представлені на фіг. 3-5. Перевірка працездатності роботи пристрою багатошарової двонаправленої асоціативної пам'яті. При поданні вхідного вектора S1  (1 1 1 1 1 1  1  1  1 1 1  1  1 111  1 1 11 1  1  1  1 1 1 1 1 1 1 ), , , , , , , , , , , , , , ,,, , , ,, , , , , , , , , , , асоційованого з S1 1 отримаємо: 1 S1Wiq  (1 1 1 1 1 1  1  1  1 1 1  1  1  1 1 1  1  1  1 1 1 1 1 1 1)  ,,,,,, , , ,,, , , ,,, , , ,,,,,, 1 10 1 Wiq 1  (34,  16, 34,  16, 34,16,  34, 34,  34,16,16,  34, 34,  34,16,16,  34, 34,  34,16,16,16, 34,16,16, ). Використовуючи функцію активації (3) при нульовому порозі, визначаємо вектор 15 S1  ( 1 1 1 1  1 1  1  1  1 1 1  1  1  1 1 1  1  1  1 1 1  1  1  1 1  1 1 1 1  1). ,,,, ,, , , ,,, , , ,,, , , ,,, , , ,, ,,,, 1 В алгоритмі функціонування пристрою багатошарової двонаправленої асоціативної пам'яті при подачі зображення на перший сенсорний вхід прийняті наступні позначення: n - число елементів у першому сенсорному шарі нейронів (у прикладі n  30 ); m - число елементів у другому сенсорному шарі нейронів (у прикладі m  30 ); g1 - число елементів у першому проміжному шарі нейронів (у прикладі g1  30 ); g2 - число елементів у другому проміжному шарі нейронів (у прикладі g2  30 ); 20 gN1 - число елементів у (N  1) -му проміжному шарі нейронів; gN - число елементів у N -му проміжному шарі нейронів; L - число наборів асоціативних зображень, що запам'ятовуються (у прикладі L  2 );  - номер набору асоціативних зображень; t1 , t1, t1 ,... 0 1 2 25 - послідовні моменти часу при отриманні асоціативних зображень, якщо t1  t1  t або в загальному вигляді k (k 1) де t - час, необхідний для отримання вихідного сигналу нейронів за допомогою функції активації; f - функція активації  -гo елемента. t1  t1  t 1 0 Алгоритм роботи багатошарової виконання наступних кроків: 30 двонаправленої 1 Wiq Крок 1. Ініціюються ваги зв'язків 1 , асоціативної Uвх.i (0)  0; Uвих.i (0)  fi (Uвх.i )  0; i  1 n; , Uв х.1 (0)  0; Uв их.1 (0)  fq1 (Uв х.1 )  0; q1  1 g1; , q1 q1 Uв х.2 (0)  0; Uв их.2 (0)  fq2 (Uв х.2 )  0; q2  1 g2; , 35 … q2 q2 передбачає 2 Wq i (i  1, n; q  1, g ) 1 1 . Задається початковий час: 1 t  t1 . Ініціюються нульовими вхідними сигналами всі нейрони мережі: 0 q1 пам'яті, q2 3 UA 108947 C2 Uв х.N (0)  0; Uв их.N (0)  fqN (Uв х.N )  0; qN  1 gN; , qN qN qN Uвх.i (0)  0; Uвих.i (0)  fj (Uвх.i )  0; j  1 m. ,    Крок 2. Для заданого зображення S  (S1 , ..., Sn ) виконуються кроки 3-7. Крок 3. Задаються вхідні сигнали нейронів  -шару: 5 Uвх.i (t1 )  Si, i  1 n. , 0 1 1 Задається час t  t1  t 0  t та обчислюються вихідні сигнали  -елементів: Uвих.і (t1)  fi (Uвх.i (t1 )), i  1 n. , 1 0 1 Крок 4. Доки не встановляться вихідні сигнали всіх   та   нейронів , виконуються кроки 5-7 алгоритму. 10 1 Крок 5. Адаптується активність елементів   шару . Обчислюються вхідні та вихідні 1 сигнали   елементів :  t   f n   i  1,n; q  1, g ; t  ; i  1,n; q  1, g . 1 Uв х.1 t1   Wiq Uв их.Xi t1 , 1 1 q1 1 i1 Uв их.1 q1 1 1  q1  Uв х.11 1 q 1 2  1 1 1 1 Вихідні сигнали   нейронів посилаються на входи елементів   шару . 15 Крок 6. Адаптується активність елементів   шару . Обчислюються вхідні та вихідні сигнали   елементів :  Uв х. i t1  2 g1  qi 1  2 Wq iUв их.Z1 t1 , 2 1     q1 i  1, n; q1  1 g1; , Uвих.i t1  fi Uвх.i t1 , i  1, n; q1  1, g1. 3 2 1 Вихідні сигнали X  нейронів посилаються на входи елементів   шару :  t   f n 20   q  1, g ; i  1,n; t  ; q  1, g ; i  1,n. 1 Uв х.1 t1   Wiq Uв их.i t1 , 3 3 q1 Uв их.1 1 i1 q1 1 4   q1  Uв х.11 q 1 3 1 1 1 1 Крок 7. Перевіряється тест на збіжність. Порівнюються вихідні сигнали   нейронів   та U Uвих.i t1 3  , i  1,n , а також вихідні сигнали   нейронів 1 вих.i t1 1   та U Uв их.1 t1 2 q1  , 1 в их.11 t 4 q q1  1 g1; які отримані на поточній на попередній ітераціях. Якщо не виконана хоч одна рівність: , 25     1 1 Uвих.i t1  Uвих.i t1 , i  1, n; Uв их.11 t 2  Uв их.11 t 4 , q1  1, g1, 3 1 q q 1 то перехід до кроку 5 алгоритму, в іншому випадку на виході нейронів   шару з'явиться  зображення S1 та здійснюється перехід до кроку 8. Для отримання наступних зображень виконуються наступні кроки алгоритму починаючи з кроку 8, коли на кожному з k шарів з   нейронів отримується одне зображення з ланцюга 30 , асоціацій, де k  1 N  1 . Крок 8. Ініціюються ваги зв'язків час: t  t (1k ) . 0 1 Wq q k ( k 1) , 2 Wq ( k 1)qk  q  1 g(k 1) , ( qk  1, gk ; (k 1) ), та задається     k Крок 9. Для заданого зображення Sk  Sk1,..., Skn , отриманого на шарі   нейронів , виконуються кроки 10-14 алгоритму. 4 UA 108947 C2 (1k ) k Крок 10. Задається час t  t1 та обчислюються вихідні сигнали   елементів :    ( Uв их.k t11k )  Uв их.k t k ; q  1, g , r qk qk k k k k де t r (r  {4,6,8,...}) - момент часу отримання вихідного сигналу з   шару елементів на попередній ітерації. 5 (k 1)  нейронів, виконуються Крок 11. Доки не встановляться вихідні сигнали всіх k  та  кроки 12-14 алгоритму. (k 1)  шару . Обчислюються вхідні та вихідні Крок 12. Адаптується активність елементів  (k 1)  елементів: сигнали    W ( Uвх.(k 1) t11k )  q( k 1) 10  t (1 k ) 2 Uвих . ( k 1) q( k 1)  t , gk (1 k ) 1 1 U qk q( k 1) вих . k qk qk 1  q(k 1)  1 g(k 1) qk  1 gk ; , , ;    (  fq( k 1)  Uвх. ( k 1) t11 k )  , , , q( k 1)   q(k 1)  1 g(k 1) ; qk  1 gk . (k 1)  нейронів посилаються на входи елементів k  шару . Вихідні сигнали  k Крок 13. Адаптується активність елементів   шару . Обчислюються вхідні та вихідні k сигнали   елементів:   W Uвх. k t (1 k )  2 qk  15  g( k 1) q( k 1) 1 2 U q( k 1) qk вих . ( k 1) q ( k 1)  t , (1 k ) 2  , qk  1 gk ; q(k 1)  1 g(k 1) ; ,   Uвих . k t (1 k )  fi  Uвх. k t (1 k )  , 3 2 , qk , qk   qk  1 gk ; q(k 1)  1 g(k 1) ; k (k 1)  шару : Вихідні сигнали   нейронів посилаються на входи елементів  Uвх.(k 1) q( k 1)  t (1k ) 3  W t , gk   qk 1 1 U qk q( k 1) вих . k q (1 k ) 3 k   Uвих . ( k 1) t (1 k )  fq( k 1)  Uвих . ( k 1) t (1 k ) 4 3 q( k 1) q( k 1)   ; q q(k 1)  1 g(k 1) ; qk  1 gk ; , , (k 1)  1 g(k 1) ; qk  1 gk . , , k Крок 14. Перевіряється тест на збіжність. Порівнюються вихідні сигнали   нейронів 20  Uвих . k t (1 k ) 3 qk Uвих . (k 1)   t (1 k ) 4  та  ( Uвих .Z k t11 k ) qk  qk  1, gk , , а також  (1 k ) U ( k 1) t (k 1)  нейронів вих . q(k 1) 2  та 1g , q (k 1) , (k 1) , які отримані на поточній на попередній ітераціях. Якщо не виконана хоч одна рівність: q( k 1)     ( Uвих .k t (1 k )  Uвих .k t11 k ) , 3 qk Uвих .(k 1) q( k 1) 25  t (1 k ) 2  U qk вих . (k 1)1) q( k   qk  1 gk ; , t (1k ) 4 , q(k 1)  1 g(k 1) , , то перехід до кроку 12 алгоритму, якщо k  1  N , то k  k  1 та перехід до кроку 8, в іншому випадку - до кроку 15. Крок 15. Ініціюються ваги зв'язків 1 Wq Крок 16. Для заданого зображення Крок 17. Задається час 30   t   ( t1N 1) Nj  SN , 2 Wjq ( j  1, m; q  1, g ) N N N    (SN1,..., SNn ) , та задається час: t  t N 1 0 . виконуються кроки 17-21 алгоритму. N та обчислюються вихідні сигнали   елементів: ( Uвих.N t1N1)  Uвих.N tN , q  1 g , r , N qN qN N N N t де r (r  {4,6,8,...}) - момент часу отримання вихідного сигналу з   шару елементів на попередній ітерації. N Крок 18. Доки не встановляться вихідні сигнали всіх   та   нейронів, виконуються кроки 19-21 алгоритму. 5 UA 108947 C2 Крок 19. Адаптується активність елементів   шару . Обчислюються вхідні та вихідні сигнали   елементів:    W U t , j  1 m; q , t   f U t , j  1, m; q  1, g . gN ( Uвх.j t1N1)  (N1) 1 qN j вих .N 1 qN qN 1 Uвих.j 5 (N1) 2 N вх.j j (N1) 1 N  1 gN; , N N Вихідні сигнали   нейронівпосилаються на входи елементів   шару . N Крок 20. Адаптується активність елементів   шару . Обчислюються вхідні та вихідні N сигнали   елементів:   W t   f U Uвх. N t (N 1)  2 qN Uвих . N qN t m 2 U jqN вих . j j 1 (N 1) 3 i вх. N qN t (N 1) 2 (N 1) 2 , ; , j  1 m; qN  1 gN; , , j  1 m; qN  1 gN. , Вихідні сигнали   нейронів посилаються на входи елементів   шару : N 10    W U t , j  1 m; q , t   f U t , j  1, m; q  1, g . gN Uвх.j t (N1)  3 1 qN j вих .N qN qN 1 Uвих.j (N1) 4 j (N1) 3 N вх.j (N1) 3 N  1 gN; , N Крок 21. Перевіряється тест на збіжність. Порівнюються вихідні сигнали   нейронів  Uвих.j t(N1) 2 15 Uвих .N qN   t (N1) 3 , q N одна рівність:   Uвих.j t(N1) 4 та   1 gN , , j  1 m , а також вихідні сигнали ,  U t (N1) N  нейронів вих .N 1 qN  та , які отримані на поточній на попередній ітераціях. Якщо не виконана хоч   ( Uвих.N t (N1)  Uвих.N t1N1) , q  1 g ; , N qN 3 qN N     Uвих .j t(N1)  Uвих .j t(N1) , j  1, m, 4 2 20 25 30 то перехід до кроку 18 алгоритму, в іншому випадку - до кроку 22. Крок 22. Зупинення. Джерела інформації: 1. Гібридна ієрархічна нейронна мережа для зберігання знань технологічного процесу механообробки / Дмитрієнко В.Д., Хавіна І.П. // Вісник НТУ "ХПІ". Тематичний випуск: Інформатика та моделювання. - Харків: НТУ "ХПІ".-2013. - №39 (1012). - С. 68-72. 2. Пат. 10024 України МПК G06G 7/00. Пристрій двоспрямованої асоціативної пам'яті / Дмитрієнко В.Д., Заковоротний О.Ю.; замовник та власник патенту Національний технічний університет "Харківський політехнічний інститут". - № u 2006 05460, заявлено 19.05.2006; опубліковано 15.11.2006, Бюл. № 11. 3. Осовский С. Нейронные сети для обработки информации. - М.: Финансы и статистика, 2002, 344 с. ФОРМУЛА ВИНАХОДУ 35 40 Пристрій багатошарової двонаправленої асоціативної пам'яті, що створений на основі пристрою двонаправленої асоціативної пам'яті, який складається з двох сенсорних шарів нейронів, який відрізняється тим, що додатково введені N шарів нейронів, які послідовно з'єднані один з одним парами двонаправлених зважених зв'язків, при цьому кожен нейрон першого з N шарів нейронів з'єднаний двонаправленими зваженими зв'язками з кожним нейроном першого сенсорного шару, а кожен нейрон останнього з N шарів нейронів з'єднаний двонаправленими зваженими зв'язками з кожним нейроном другого сенсорного шару нейронів. 6 UA 108947 C2 7 UA 108947 C2 8 UA 108947 C2 Комп’ютерна верстка Л. Бурлак Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 9