Спосіб псевдовипадкового завадостійкого кодування

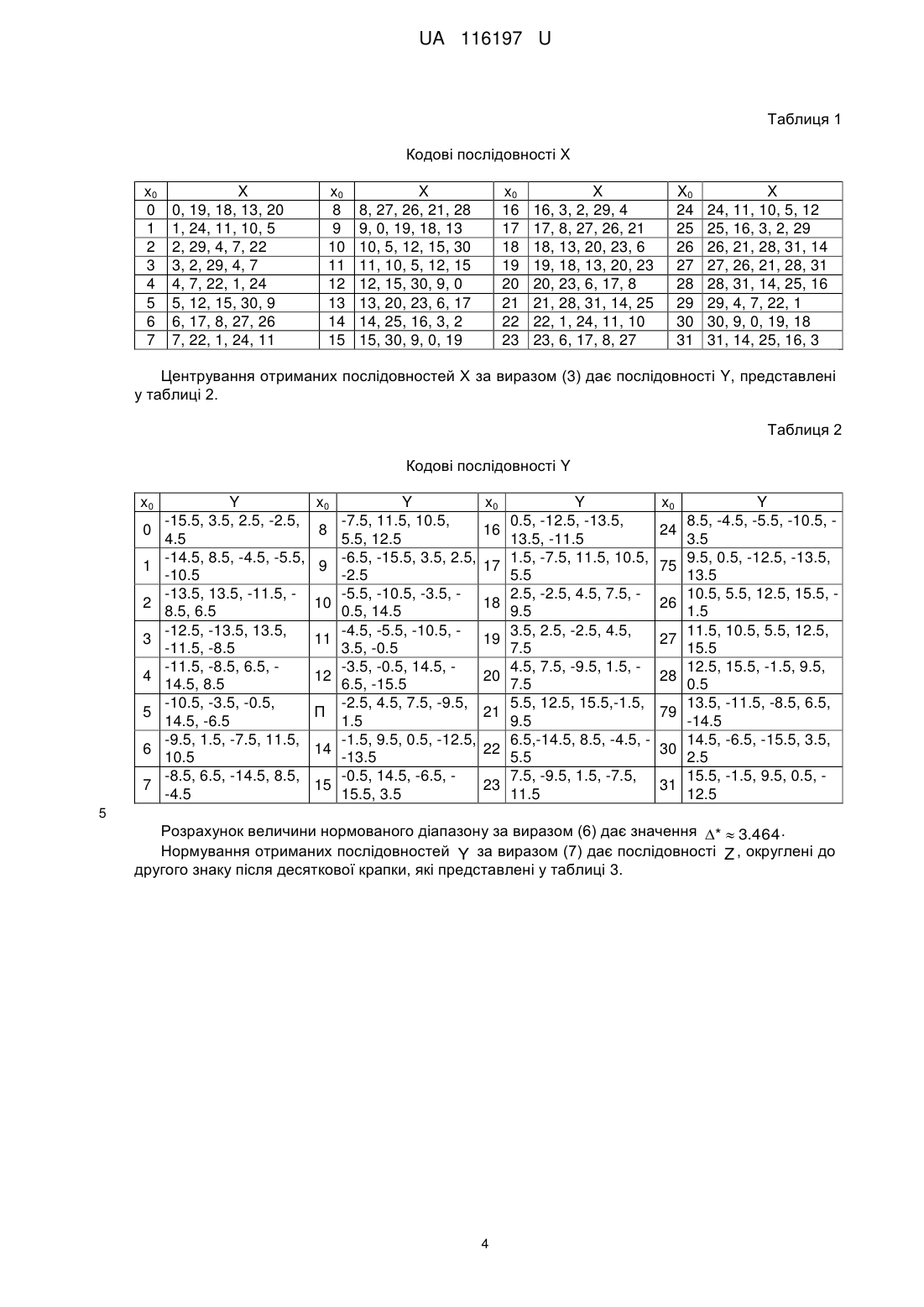
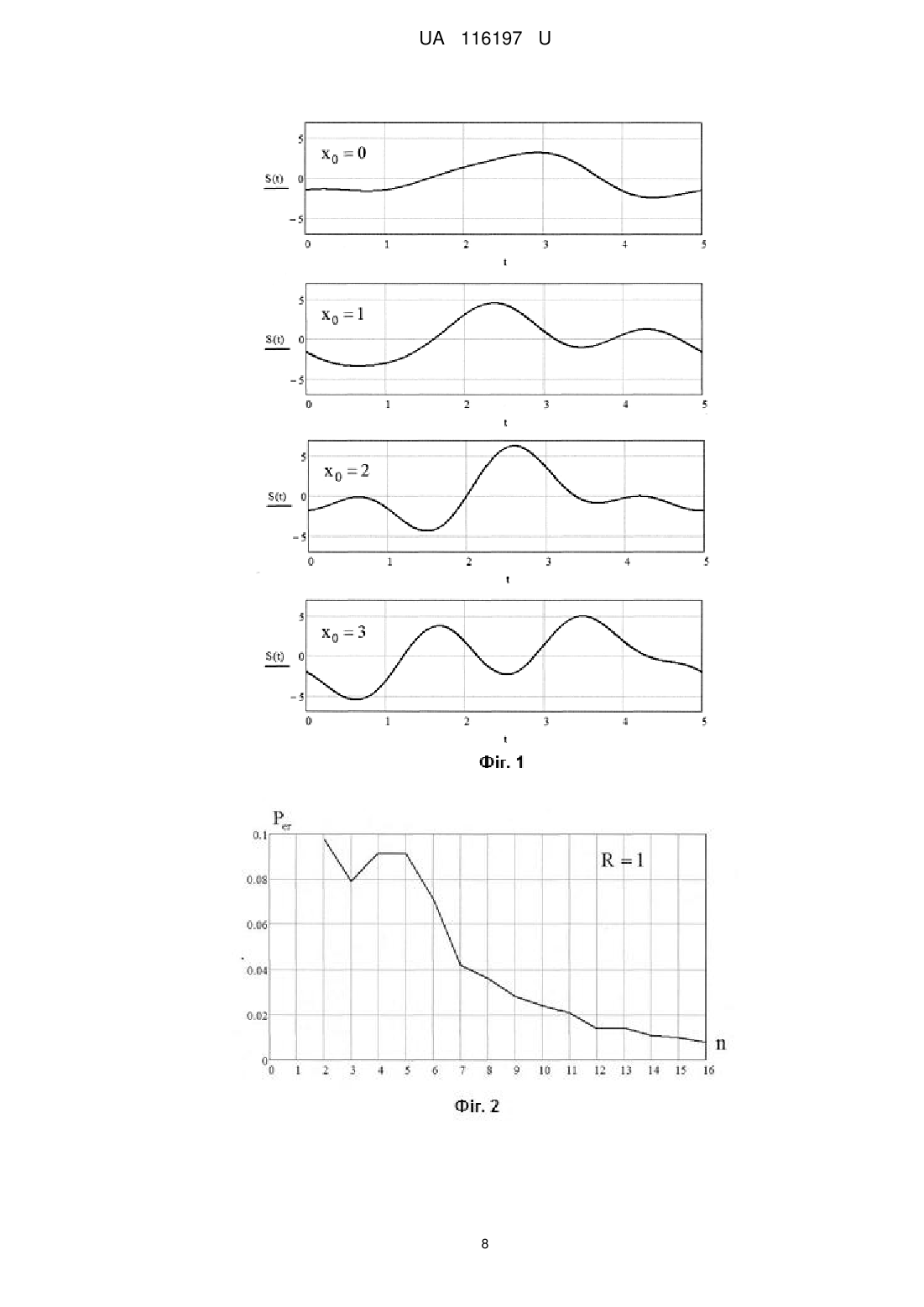
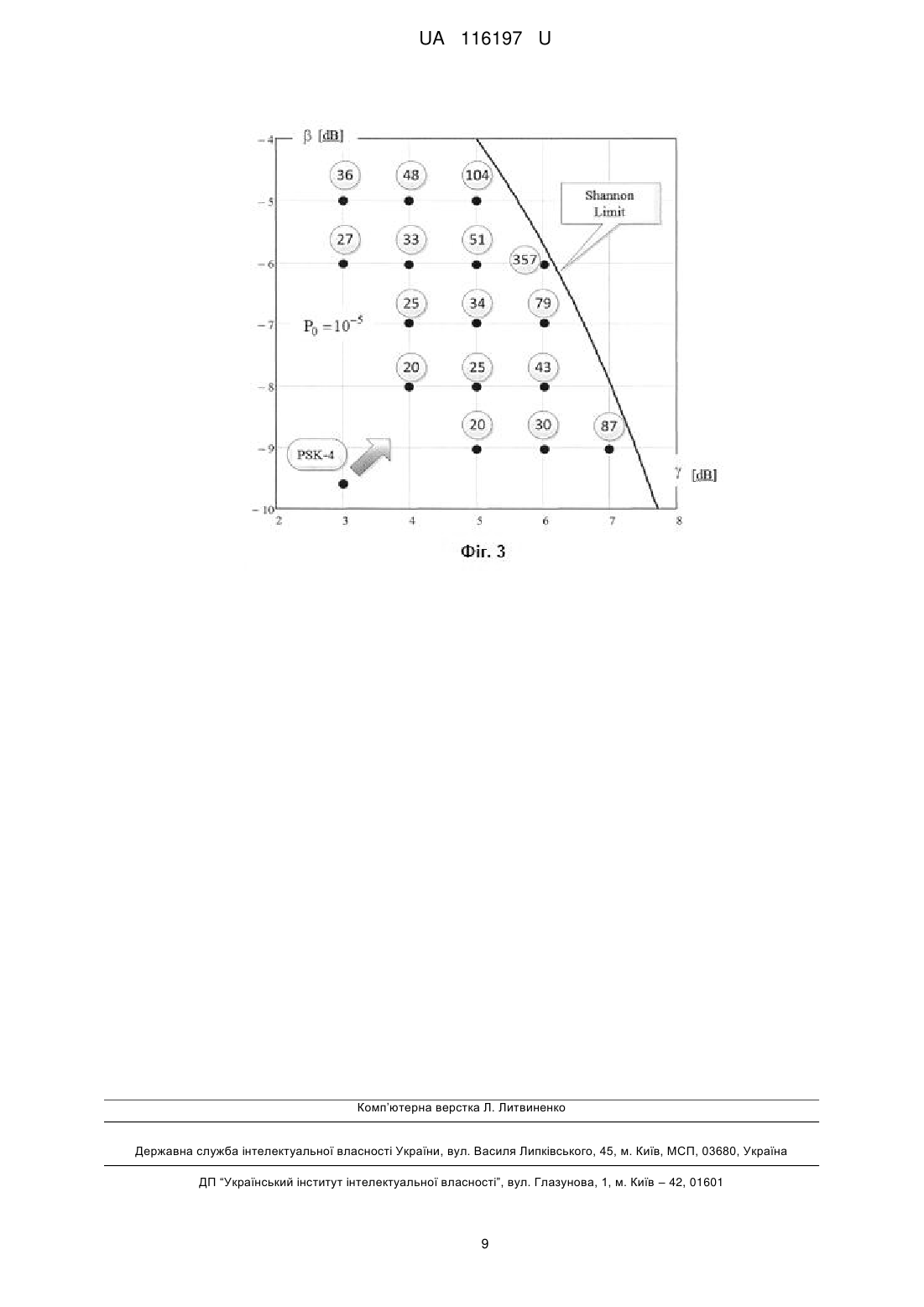
Реферат: UA 116197 U UA 116197 U 5 10 15 20 25 30 35 40 45 50 Корисна модель належить до області завадостійкого кодування і реалізує наближення частотно-енергетичної ефективності систем передачі інформації до теоретичної межі Шеннона, може бути використана в системах стільникового зв'язку 5G. Відомий спосіб генерації псевдовипадкових послідовностей [1]. Для генерації псевдовипадкової послідовності використовують операцію підсумовування по модулю два попередніх біт послідовності. Недолік способу - низькі функціональні можливості, оскільки процедура побудови коду на основі псевдовипадкової послідовності не визначена. Відомий також спосіб кодування чисел [2]. Розглянуто спосіб завадостійкого кодування, який містить операції випадкового генерування чисел - символів коду та процедуру виключення "поганих" кодових слів при їх побудові чисто випадковими способами. Недолік способу - низькі функціональні можливості, оскільки процес отримання випадкових чисел та порядок побудови кодових слів - не визначено. Найбільш близьким за технічною суттю (прототипом) є спосіб псевдовипадкового завадостійкого кодування, що полягає у формуванні вибірок безперервного шуму [3]. Суть способу-прототипу полягає в генерації m  2k вибірок безперервного шуму, кожна тривалістю Т. Даним вибіркам ставляться у відповідність двійкові числа із діапазону i 0, m  1 . В кодері послідовності повідомлень джерела розбиваються на групи по k двійкових символів і для кожної групи як сигнал передається відповідна вибірка шуму. При цьому суть процесу отримання вибірок безперервного шуму не визначена. Це не дає можливості практичної реалізації псевдовипадкового завадостійкого кодування. Недолік способу-прототипу - низькі функціональні можливості, які обумовлені неможливістю практичної реалізації способу псевдовипадкового завадостійкого кодування. В основу запропонованої корисної моделі поставлена задача розширити функціональні можливості способу-прототипу за рахунок розробки та впровадження конструктивної технології формування вибірок неперервного шуму на основі детермінованої технології лінійної конгруентної генерації, що дає можливість на 2-3 децибели підвищити показники питомої частотної і енергетичної ефективності систем передачі інформації. Поставлена задача вирішується за рахунок того, що при формуванні кожної із вибірок неперервного шуму двійкова послідовність - інформаційне повідомлення довжиною k - біт перетворюють в десяткове число х0, еквівалентне кількісному значенню двійкової послідовності, та вибирають за перший символ n-символьного недвійкового кодового слова псевдовипадкового завадостійкого коду, решту n  1 недвійкових чисел кодового слова генерують на основі технології лінійної конгруентної генерації, після чого отримані числа кодового слова центрують відносно нуля, нормують по абсолютній величині відповідно до виділеної для передачі кодового символу енергії і використовують як інформативні параметри сигналу - амплітуди квадратур піднесучих коливань у гармонійному ортогональному розкладанні Фур'є. Запропонований спосіб реалізують наступним чином. Загальний потік символів джерела, призначений для передачі, розбивають на блоки по k біт для побудови блокового завадостійкого коду. При цьому кожну комбінацію з k двійкових символів джерела трактують як десяткову кількісну величину x 0 - порядковий номер, який визначає подальшу відповідну послідовність псевдовипадкових чисел x1, x 2,..., xn1 тобто x 0 число, що породжує кодове слово з відповідним номером. Таким чином, кожному блоку з k двійкових символів джерела ставлять у відповідність блок з n недвійкових чисел коду. Величина k (1) R n є швидкістю завадостійкого коду та показує співвідношення кількості інформаційних двійкових символів повідомлення до кількості недвійкових символів коду, призначених для передачі по каналу зв'язку. Процес кодування полягає в обчисленні послідовності символів кодового слова на підставі відомого породжуючого числа x 0 . Отримання n  1 чисел кодового слова на основі числа x 0 здійснюється на основі детермінованої технології лінійної конгруентної генерації (ЛКГ). Властивість лінійності цієї технології є принциповою, оскільки без її виконання код буде не придатним для реалізації у наступному обчислювально-простого способу декодування. Значення числових символів кодових слів обчислюють відповідно до таких правил: 1 UA 116197 U 5 10 15 - x 0  [0...( 2k  1)] - початковий символ - умовний порядковий номер повідомленняджерела, що породжує кодове слово; - xi  (a  xi1  b) mod m , i  1 n  1) - числа кодового слова псевдовипадкового коду, які ,...( обчислюють по рекурентному способу, де операція ( A ) mod m - означає обчислення A по модулю m ; - a, b - константи, m - модуль обчислень; - a, b, m - цілі позитивні числа, що задовольняють умовам: m  2k ; b і m - взаємно прості числа, при цьому величини (a  1) і m вибирають кратними 4. При виконанні вказаних вище умов псевдовипадкові цілі числа, що отримуються, розподілені рівномірно у діапазоні [0,2k  1] , а їх послідовність має максимальні значення періоду повторення. Причому довільне і-те число послідовності кодового слова зв'язане з початковим породжуючим числом x 0 залежністю:  ai  1  x i   ai  x 0  b  mod m, i  1,...n  1 . (2)  a 1    Далі, для мінімізації потрібної потужності передатчика числа кодових слів, що отримані, центрують відносно нуля, тобто послідовність X  x0, x1,..., xn1 перетворюють у послідовність Y  y0, y1,..., yn1 , де m 1 (3) , i  0,1,..., n  1 . 2 Числа послідовності Y вже не є цілими, представляють дискретний ряд з кроком 1 та yi  xi  рівномірно розподілені у діапазоні 20 25  m  1 m  1 , абсолютна величина якого складає  2 , 2      (m  1) . Далі числа послідовності Y нормують відповідно до виділеної для передачі кодового слова енергії. Нехай значення середньої енергії, яку можливо витратити відповідно до виділеного бюджету енергії на передачу одного двійкового символу джерела, є величиною Eb . Тоді для передачі одного символу коду в каналі допустимо витратити енергію (4) Eсимв  R  Eb , де R - швидкість коду, що визначається виразом (1). Числа кодового слова розподілені по дискретному рівномірному закону всередині діапазону  навколо нуля. При цьому дисперсія D (середня потужність)довільного символу складає величину приблизно 2 . (5) 12 На підставі визначення дисперсії рівномірного розподілу і введеного обмеження на енергію символу, визначають вимоги до величини нормованого діапазону  * , шляхом використання виразів (4) і (5): D  *2    R  E 30 35 3 (6)  R  Eb . b  *  2 12  де  - передбачена тривалість передачі одного символу коду в каналі, яка визначається швидкістю модуляції. Знайдену величину  * використовують в подальшому для нормування значень псевдовипадкових чисел відповідно до виділеного бюджету енергії. Процес нормування чисел центрованої відносно нуля послідовності Y полягає у обчисленнях елементів нової послідовності Z  z0, z1,..., zn1 за наступною формулою: * (7) , i  0,1,..., n  1 .  Отриману послідовність чисел Z  z0, z1,..., zn1 використовують далі для побудови канальної форми загального сигналу кодового слова на основі гармонійного ортогонального розкладення Фур'є на тривалості n   : zi  y i  2 UA 116197 U  n 1  2   i   t      zi  Cos 2 fн  n     i0   2 . St      n    (8) n  n 1 j      2 t     z j  Sin 2 fн  n       n      j 2        В виразі (8): - величина fн позначає частоту несучого коливання сигналу для передавання кодового слова; n  j  i ,   2  - відповідно, i( j) -ти піднесучі частоти; - величини  fн    fн  n   n       5 10 15 20 25 30 2 введено для забезпечення збереження виділеного бюджету енергії на n передачу кодового символу (4), оскільки числа zi використовують як амплітуди гармонійних коливань. Згідно з корисною моделлю, загальний сигнал кодового слова псевдовипадкового завадостійкого коду передбачає паралельне кодування недвійкових символів (чисел) коду як амплітуд ортогональних на тривалості T  n   гармонійних піднесучих коливань. При цьому за час T передбачається паралельна передача n символів кодового слова. Таким чином, суть способу - корисної моделі, що розглядається, полягає в введенні до способу-прототипу та виконанні наступних нових операцій: - перетворення інформаційного повідомлення довжиною k біт в десяткове число x 0 , еквівалентне кількісному значенню двійкової послідовності; - генерації решти n  1 недвійкових символів кодового слова за технологією лінійної конгруентної генерації; - центрування чисел кодового слова відносно нуля; - нормування чисел кодового слова відповідно до виділеної для передачі кодового слова енергії; - побудови загального сигналу кодового слова у вигляді гармонійного ортогонального розкладення Фур'є. Вираз (8) описує практичну реалізацію вибірки випадкового (псевдовипадкового) відрізку безперервного шуму. Отримання загального сигналу (8) за викладеним способом, фактично, є конструктивною технологією отримання вибірок безперервного шуму, що означає усунення основного недоліку способу-прототипу та досягнення мети корисної моделі - розширення функціональних можливостей. Розглянемо конкретний приклад застосування запропонованого способу для побудови псевдовипадкового завадостійкого коду. Нехай параметри псевдовипадкового завадостійкого коду складають значення: k  5 , n  5 , - множник R  1,   31, Eb  1 Вт  с  , fн  1 Гц  ,   1c . Для технології ЛКГ вибираємо параметри: 5 m  22  32 , a  5 , b  19 . Послідовно перебираючи номери двійкових послідовностей на довжині k  5 символів x0  0,1 31 , використаємо правило (2) для отримання набору ,... 35 40 послідовностей X , які представлені у таблиці 1. Наприклад, при кодуванні двійкового повідомлення вигляду "00000" (при k  5 ) маємо: x0  0 - (перетворення двійкової комбінації "00000" в десяткове число); x1  a  x0  bmod m  5  0  19 mod 32  19 ; x2  a  x1  bmod m  5  19  19 mod 32  18 ; x3  a  x2  bmod m  5  18  19 mod 32  13 ; x 4  a  x3  bmod m  5  13  19 mod 32  20 . 3 UA 116197 U Таблиця 1 Кодові послідовності X x0 0 1 2 3 4 5 6 7 X 0, 19, 18, 13, 20 1, 24, 11, 10, 5 2, 29, 4, 7, 22 3, 2, 29, 4, 7 4, 7, 22, 1, 24 5, 12, 15, 30, 9 6, 17, 8, 27, 26 7, 22, 1, 24, 11 x0 8 9 10 11 12 13 14 15 X 8, 27, 26, 21, 28 9, 0, 19, 18, 13 10, 5, 12, 15, 30 11, 10, 5, 12, 15 12, 15, 30, 9, 0 13, 20, 23, 6, 17 14, 25, 16, 3, 2 15, 30, 9, 0, 19 x0 16 17 18 19 20 21 22 23 X 16, 3, 2, 29, 4 17, 8, 27, 26, 21 18, 13, 20, 23, 6 19, 18, 13, 20, 23 20, 23, 6, 17, 8 21, 28, 31, 14, 25 22, 1, 24, 11, 10 23, 6, 17, 8, 27 X0 24 25 26 27 28 29 30 31 X 24, 11, 10, 5, 12 25, 16, 3, 2, 29 26, 21, 28, 31, 14 27, 26, 21, 28, 31 28, 31, 14, 25, 16 29, 4, 7, 22, 1 30, 9, 0, 19, 18 31, 14, 25, 16, 3 Центрування отриманих послідовностей Х за виразом (3) дає послідовності Y, представлені у таблиці 2. Таблиця 2 Кодові послідовності Y x0 0 1 2 3 4 5 6 7 Y -15.5, 3.5, 2.5, -2.5, 4.5 -14.5, 8.5, -4.5, -5.5, -10.5 -13.5, 13.5, -11.5, 8.5, 6.5 -12.5, -13.5, 13.5, -11.5, -8.5 -11.5, -8.5, 6.5, 14.5, 8.5 -10.5, -3.5, -0.5, 14.5, -6.5 -9.5, 1.5, -7.5, 11.5, 10.5 -8.5, 6.5, -14.5, 8.5, -4.5 x0 8 9 10 11 12 П 14 15 Y -7.5, 11.5, 10.5, 5.5, 12.5 -6.5, -15.5, 3.5, 2.5, -2.5 -5.5, -10.5, -3.5, 0.5, 14.5 -4.5, -5.5, -10.5, 3.5, -0.5 -3.5, -0.5, 14.5, 6.5, -15.5 -2.5, 4.5, 7.5, -9.5, 1.5 -1.5, 9.5, 0.5, -12.5, -13.5 -0.5, 14.5, -6.5, 15.5, 3.5 x0 16 17 18 19 20 21 22 23 Y 0.5, -12.5, -13.5, 13.5, -11.5 1.5, -7.5, 11.5, 10.5, 5.5 2.5, -2.5, 4.5, 7.5, 9.5 3.5, 2.5, -2.5, 4.5, 7.5 4.5, 7.5, -9.5, 1.5, 7.5 5.5, 12.5, 15.5,-1.5, 9.5 6.5,-14.5, 8.5, -4.5, 5.5 7.5, -9.5, 1.5, -7.5, 11.5 x0 24 75 26 27 28 79 30 31 Y 8.5, -4.5, -5.5, -10.5, 3.5 9.5, 0.5, -12.5, -13.5, 13.5 10.5, 5.5, 12.5, 15.5, 1.5 11.5, 10.5, 5.5, 12.5, 15.5 12.5, 15.5, -1.5, 9.5, 0.5 13.5, -11.5, -8.5, 6.5, -14.5 14.5, -6.5, -15.5, 3.5, 2.5 15.5, -1.5, 9.5, 0.5, 12.5 5 Розрахунок величини нормованого діапазону за виразом (6) дає значення *  3.464 . Нормування отриманих послідовностей Y за виразом (7) дає послідовності Z , округлені до другого знаку після десяткової крапки, які представлені у таблиці 3. 4 UA 116197 U Таблиця 3 Кодові послідовності Z x0 0 1 2 3 4 5 6 7 Z -1.73, 0.39, 0.28, 0.28, 0.5 -1.62, 0.95, -0.5, 0.61, -1.17 -1.51, 1.51, -1.29, 0.95, 0.73 -1.4, -1.51, 1.51, 1.29, -0.95 -1.29, -0.95, 0.73, 1.62, 0.95 -1.17, -0.39, -0.06, 1.62, -0.73 -1.06, 0.17, -0.84, 1.29, 1.17 -0.95, 0.73, -1.62, 0.95, -0.5 x0 8 9 10 11 12 13 14 15 Z -0.84, 1.29, 1.17, 0.61, 1.4 -0.73, -1.73, 0.39, 0.28, -0.28 -0.61, -1.17, -0.39, 0.06, 1.62 -0.5, -0.61, -1.17, 0.39, -0.06 -0.39, -0.06, 1.62, 0.73, -1.73 -0.28, 0.5, 0.84, 1.06, 0.17 -0.17, 1.06, 0.06, 1.4, -1.51 -0.06, 1.62, -0.73, 1.73, 0.39 x0 16 17 18 19 20 21 22 23 Z 0.06, -1.4, -1.51, 1.51, -1.29 0.17, -0.84, 1.29, 1.17, 0.61 0.28, -0.28, 0.5, 0.84, -1.06 0.39, 0.28, -0.28, 0.5, 0.84 0.5, 0.84, -1.06, 0.17, -0.84 0.61, 1.4, 1.73, 0.17, 1.06 0.73, -1.62, 0.95, 0.5, -0.61 0.84, -1.06, 0.17, 0.84, 1.29 x0 Z 0.95, -0.5, -0.61, -1.17, 24 -0.39 1.06, 0.06, -1.4, -1.51, 25 1.51 1.17, 0.61, 1.4, 1.73, 26 -0.17 1.29, 1.17, 0.61, 1.4, 27 1.73 1.4, 1.73, -0.17, 1.06, 28 0.06 1.51, -1.29, -0.95, 0.73, 29 -1.62 1.62, -0.73, -1.73, 0.39, 30 0.28 1.73, -0.17, 1.06, 0.06, 31 -1.4 У відповідності з виразом (8) при заданих параметрах коду повний сигнал довільного кодового слова, який є готовим для передачі по каналу, матиме вигляд: St   2   1 i     zi  Cos 2  t     5 5  2 i 0   4  n   1 j  3    z  Sin 2  t    j 5    5  j3  (9) , 5 10 15 20 25 де як zi вибираються послідовності з комірок таблиці 3 у відповідності з фактичним значенням x 0 . Оскільки у прикладі, що розглядається, величина n непарна, то для кодування чисел zi коду використано три косинусні та дві синусні квадратурні компоненти піднесучих коливань (нерівна кількість). Приклади вигляду повних сигналів кодових слів, які обчислені за виразом (9) та ілюструють результат застосування корисної моделі - способу псевдовипадкового кодування для повідомлень з номерами 03 показані на фіг. 1. Для декодування псевдовипадкового завадостійкого коду (яке не є предметом розгляду в даній корисної моделі) та оцінки значень чисел zi , приймачу достатньо виконувати обчислення відповідних коефіцієнтів розкладення St  в ряд Фур'є на інтервалі часу, рівному T  n   , а потім, з використанням операцій, зворотних нормуванню та центруванню, отримати номер двійкової послідовності джерела x 0 . Розглянемо корисний ефект, що досягається при використанні розглянутого способу реалізації псевдовипадкового завадостійкого кодування при його використанні в умовах білого гауссового шуму в каналі передачі інформації. Доцільним є проведення порівняння зі звичайними способами надлишкового завадостійкого кодування. Для оцінки коригувальних властивостей коду, побудованого пропонованим способом, було проведено моделювання гауссового каналу і декодування кодових слів за правилом максимальної правдоподібності в умовах спотворень канальних символів при параметрах коду, які наведені у розглянутому вище прикладі конкретного застосування. При цьому досліджувалась залежність ймовірності декодування з помилкою Per від довжини кодового слова n при фіксованої швидкості коду R  1 і відношенні сигнал/шум h, нормованого до одного біту інформаційного повідомлення h  Eb N0  4 , де N0 - спектральна щільність потужності адитивного білого гауссового шуму. Результати моделювання у вигляді залежності ймовірності декодування з помилкою на блок Per як функції довжини блока n представлені на графіку (фіг. 5 UA 116197 U 5 10 15 2). Слід підкреслити, що, незважаючи на наявність викидів при малих значеннях довжини блока, досліджена ймовірність Per має монотонно спадаючий характер з ростом довжини блока n. При цьому декодування проводилося за правилом максимальної правдоподібності з визначенням найближчого слова з повної кодової книги до прийнятого кодового слова. Отже, простим збільшенням довжини блока псевдовипадкового коду можливо досягнути будь-якого потрібного малого значення ймовірності декодування з помилкою. Оцінка отриманого виграшу при використанні запропонованого коду в порівнянні з некодованою модуляцією і всіма існуючими комбінаторними кодами може бути проведена на площині частотно-енергетичної ефективності систем передачі інформації. Координатами на даній площині є показники питомої енергетичної ефективності   1/ h , де h - відношення сигнал/шум, а також показник питомої частотної ефективності   1/ F , де F - смуга частот сигналу. Ці покажчики виражені в децибелах і нормовані до одного біту повідомлень. Так як числа, що генеруються за псевдовипадковим законом, розподілені, практично, рівномірно у визначеному діапазоні, то кодова книга у n-вимірному просторі утворює Пуассонове поле точок. На виході гауссового каналу при оптимальному когерентному оцінюванні числових символів коду, точки, що приймаються, розташовуються (навколо справжніх) всередині сфери невизначеності з радіусом rN  n  N0 / 2 . Тому, ймовірність 0 декодування з помилкою для цього поля можна визначити, як ймовірність події, котра складається з потрапляння всередину сфери з радіусом rN , хоча б однієї точки, крім істинної: 0 20      Per  1  exp    V rN0 , де V rN0 - сфера невизначеності шуму, n  N  n  V rN0     n 0  Г  1 ,  2  2    Г( x ) - гамма функція;  - щільність поля точок, яка визначається з виразів:   n 25 30 35 40 45  N  2    n   0  R  Eb      2  ;   2Rn V r  , V r    n  Г  1 2  Vr  - загальний сферичний обсяг існуючих точок поля при обліку можливих шумових зсувів. Тоді ймовірність помилки на блок коду складає величину    n  Per  1  exp  2R 1  2  R  h  .   Оскільки запропонований код є неузгодженим за розміщенням точок кодових слів зі значеннями комбінацій двійкових символів k-бітових блоків повідомлень джерела, то ймовірність помилки на біт визначається співвідношенням: P0  0,5  Per . На основі дослідження статистичних властивостей і наведеної аналітичної моделі коду був проведений розрахунок необхідних довжин блока коду для досягнення значення P0  10 5 . Результати моделювання та розрахунків представлені точками на площині ефективності на кресленні (фіг. 3). Цифри, які зображені на площі ефективності всередині окружностей, є необхідними значеннями довжини блока псевдовипадкового завадостійкого коду. На фіг. 3 показана область площі ефективності, розташована правіше і вище відносно точки некодованої квадратурної модуляції (PSK-4). Слід зазначити, що жодна відображуюча точка існуючих комбінаторних кодів не розташовується одночасно вище і правіше PSK-4. Тому всі точки реалізацій запропонованого коду на фіг. 3 (із зазначеними значеннями необхідної довжини блока) виграють за питомою частотною або енергетичною ефективністю, як мінімум 23 децибели у всіх відомих кодів. При довжині блока n, рівній приблизно 20-40 канальних символів, при різних швидкостях коду можна забезпечити виграш в порівнянні з некодованою модуляцією до 3 і більше децибелів по питомій швидкості та(або) по зниженню необхідної питомої енергії на передачу одного біта інформаційних повідомлень. Таким чином, технічний результат від використання запропонованої корисної моделі дозволяє розширити функціональні можливості способу-прототипу та отримати практичний спосіб псевдовипадкового завадостійкого кодування. Даний спосіб дозволяє практично генерувати вибірки безперервного шуму, що, в свою чергу, надає можливість підвищити 6 UA 116197 U 5 10 достовірність передачі даних та зменшити питомі витрати на передачу інформації. Наведені приклади, математичні вирази та результати моделювання і розрахунків підтверджують достовірність отриманих результатів. Джерела інформації: 1. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. - Издательский дом "Вильямс", 2003.-743-744. 2. Флейшман Б.С. Конструктивные способы оптимального кодирования для каналов с шумами. - М.: Изд. АН СССР, 1963. - 224 с. 3. Shannon С.Е. A Mathematical Theory of Communication. - Bell Syst. Tech., July-October, 1948. - Vol. 27. - P. 379-423, 623-656. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 15 20 25 Спосіб псевдовипадкового завадостійкого кодування, що полягає у формуванні вибірок k неперервного шуму, кожна з яких відповідає двійковому числу з діапазону і[0,2 -1], який відрізняється тим, що при формуванні кожної із вибірок інформаційне повідомлення - двійкову послідовність довжиною k-біт перетворюють в десяткове число х0, еквівалентне кількісному значенню двійкової послідовності, та вибирають за перший символ n-символьного недвійкового кодового слова псевдовипадкового завадостійкого коду, решту (n-1) недвійкових чисел кодового слова генерують на основі технології лінійної конгруентної генерації, після чого отримані числа кодового слова центрують відносно нуля, нормують по абсолютній величині відповідно до виділеної для передачі кодового символу енергії і використовують як інформативні параметри сигналу - амплітуди квадратур піднесучих коливань у гармонійному ортогональному розкладанні Фур'є. 7 UA 116197 U 8 UA 116197 U Комп’ютерна верстка Л. Литвиненко Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 9