Спосіб криптографічного перетворення двійкових даних (варіанти)

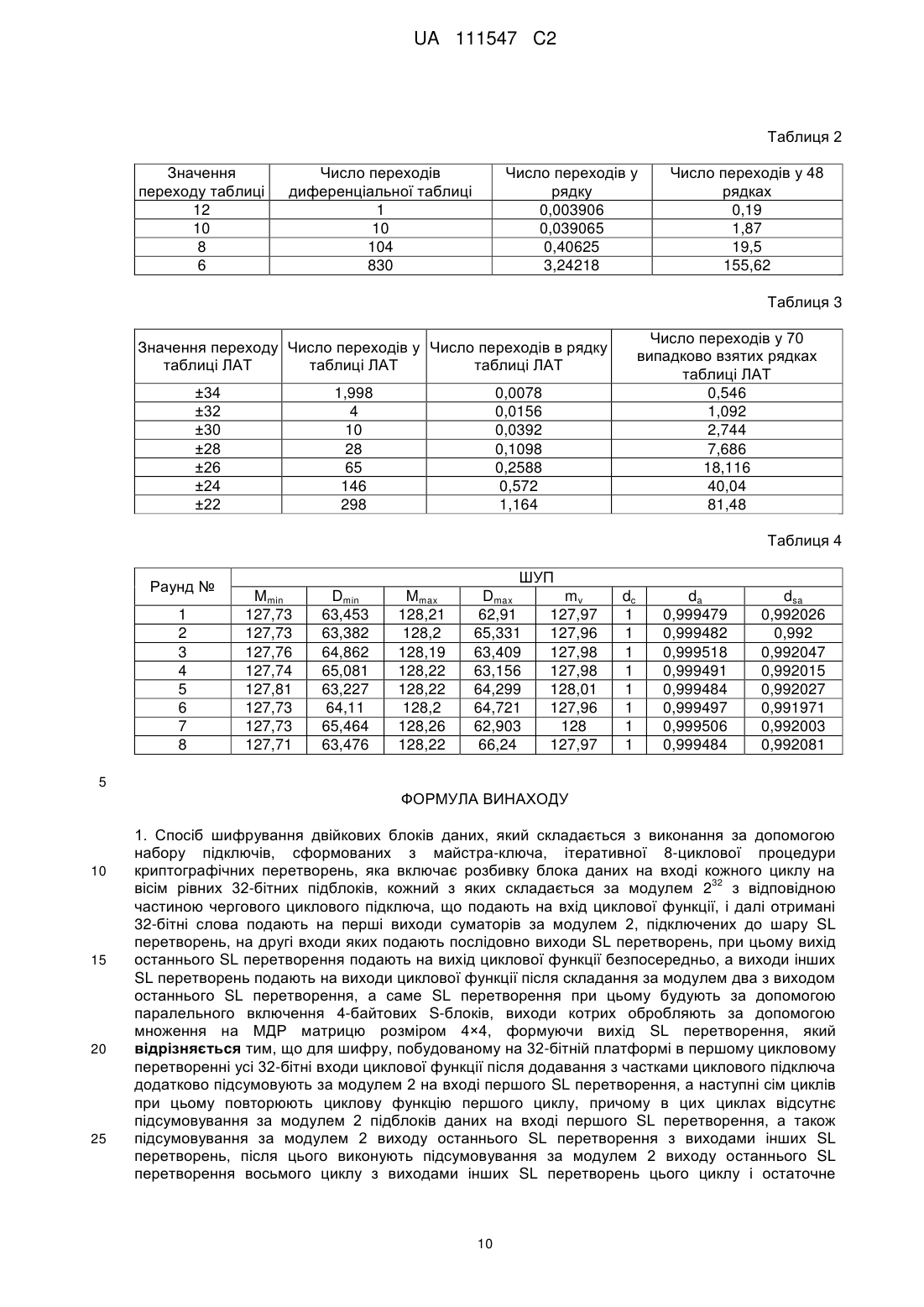
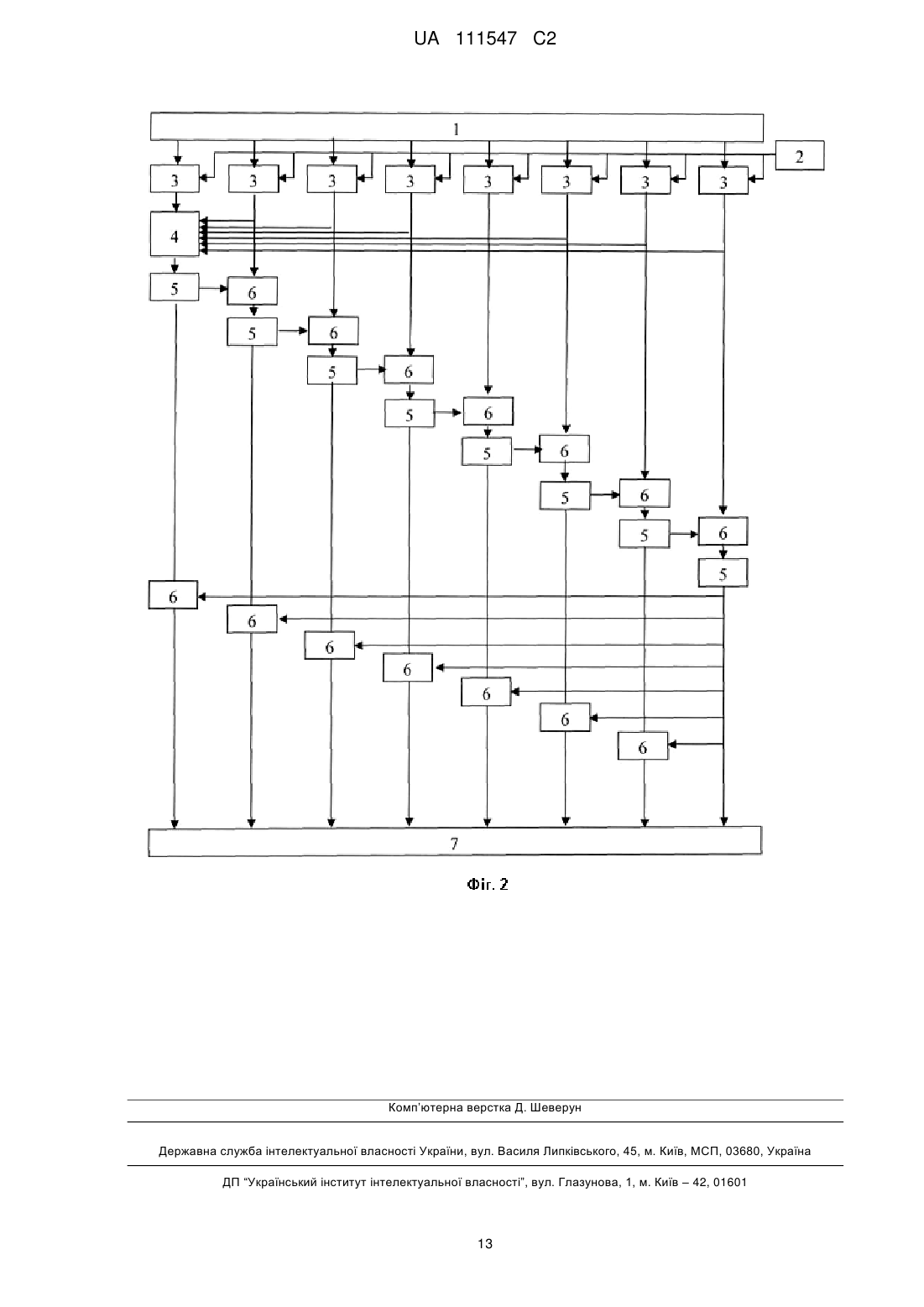
Реферат: Винахід належить до області обчислювальної техніки, а саме до способів криптографічного перетворення даних. Спосіб криптографічного перетворення двійкових даних, складається з виконання за допомогою набору підключів, сформованих з майстра-ключа, ітеративної 8циклової процедури криптографічних перетворень, яка включає розбивку блока даних на вході 32 кожного циклу на вісім рівних 32-бітних підблоків, кожний з яких складається за модулем 2 з відповідною частиною чергового циклового підключа, що подається на вхід циклової функції, і далі отримані 32-бітні слова подаються на перші виходи суматорів за модулем 2, підключених до шару SL перетворень, на другі входи яких подаються послідовно виходи SL перетворень, при цьому вихід останнього SL перетворення подається на вихід циклової функції UA 111547 C2 (12) UA 111547 C2 безпосередньо, а виходи інших SL перетворень подаються на виходи циклової функції після складання за модулем два з виходом останнього SL перетворення, а саме SL перетворення при цьому будується за допомогою паралельного включення 4-байтових S-блоків, виходи котрих обробляються за допомогою множення на МДР матрицю розміром 4×4 формуючи вихід SL перетворення, а для 64-бітної платформи вхідний блок даних (256-ти бітів) на вході першого циклу розбивається на чотири рівних 64-бітних підблоків, кожний з яких складається за 64 модулем 2 з відповідною часткою чергового циклового підключа, що подається на вхід циклової функції, a SL перетворення будуються на основі обробки 64-бітних блоків даних вісьма байтовими S-блоками з подальшим множенням результатів проходження S-блоків на МДВ матрицю розміром 8×8, формуючи вихід SL перетворення, а наступні сім циклів при цьому повторюють циклову функцію першого циклу за винятком того, що в цих циклах відсутнє підсумовування за модулем 2 підблоків даних на вході першого SL перетворення, а також підсумовування за модулем 2 виходу останнього SL перетворення з виходами інших SL перетворень, після цього виконується підсумовування за модулем 2 виходу останнього SL перетворення восьмого циклу з виходами інших SL перетворень цього циклу і остаточне підсумовування результату з останнім цикловим підключем за модулем 2, при цьому процедура розгортання майстра-ключа включає його поділ на окремі байти з подальшим виконанням циклічного зсуву майстра-ключа на числа бітів, що задаються значеннями послідовності суміжних (сусідніх) байтів і отримані циклічні зрушення майстра-ключа використовуються послідовно як чергові циклові підключи. Технічним результатом, що досягається даним винаходом, є підвищення показників стійкості, розширення функціональних можливостей. UA 111547 C2 5 10 15 20 25 30 35 40 45 50 55 Винахід належить до області обчислювальної техніки, а саме до способів криптографічного перетворення даних. Відомий спосіб недетермінованого криптографічного перетворення даних (Деклараційній патент на України на корисну модель № 53949А, МПК 17.02.2003. Бюл. № 2). Спосіб включає формування ключа шифрування у вигляді сукупності підключів і почергове перетворення підблоків на основі керованої підстановки (байтової заміни), в котрому таблиця підстановок представляється латинським квадратом, розмірність якого визначається підблоком, що підлягає зашифруванню, а само перетворення здійснюється на основі керованої підстановки шляхом вибору як вихідні байти значень комірок таблиць, які визначаються за першими (інформаційними) входами в таблиці підстановок (латинських квадратів) по рядках (стовпцях), значеннями підблоків, що шифруються на поточному кроці, і за другими (керуючими) входами в таблиці підстановок по стовпцях (рядках), що визначаються байтовими значеннями виходів таблиць підстановок на попередніх кроках перетворення блоків даних по черзі в двох напрямках, причому в одному напрямку використовують підстановки-рядки, в іншому підстановки-стовпці латинських квадратів, а між перетвореннями в кожному з напрямків вводять операцію складання підблоків даних з ключем, який вибирають параметрично залежним від значення останнього зашифрованого підблока попередньої поточної операції керованої підстановки. Недоліком цього способу є необхідність виділення значного обсягу пам'яті для зберігання таблиць підстановок (латинських квадратів) великого розміру (для байтових підстановок 16 24 латинський квадрат містить 2 комірок - це 2  17-ть Мбіт пам'яті), що створює труднощі у використанні шифру в ряді практичних додатків. Найбільш близьким за сукупністю суттєвих ознак до способу, який заявляється, є спосіб, реалізований у шифрі "Мухомор-512" (див. Горбенко І.Д. Перспективний блоковий симетричний шифр "Мухомор" - основні положення та специфікація / І.Д. Горбенко, М.Ф. Бондаренко, В.І. Долгов, Р.В. Олійников та інші // Прикладная радиоэлектроника. - Харьков: ХТУРЭ. - 2007. Том. 6, № 2. - С. 147-157), котрий полягає у виконанні багатоциклової процедури криптографічних перетворень, які виконуються за допомогою набору підключів і складаються з первинного забілювання вихідного блока даних за допомогою додавання за модулем 2 з першим підключем та наступних ітеративних циклових перетворень, кожне з яких включає в себе розбивку вхідного блока даних на 4-ри рівних підблоки, різниця (XOR) між парами яких подається на вхід функції ускладнення М-256 (для розміру блоків даних 512 бітів), крім того, ці 4-ри підблоки складаються попарно за модулем 2 із вихідними підблоками функції ускладнення, після чого другий і четвертий підблоки подаються на вихід циклової функції безпосередньо, а першій і третій підблоки подаються на вихід циклової функції після проходження операції ортогонального перетворення, тобто як базова схема циклового перетворення використовується схема Лея-Массея [1]. Функція ускладнення шифру Мухомор 512. 32-х бітні вхідні значення функції М-256 32 переставляються між собою і складаються за модулем 2 з відповідними частками чергового підключа, що також подається на вхід функції. Потім кожне отримане 32-х бітне слово проходить окреме SL перетворення, число котрих дорівнює числу 32-х бітних слів, причому результати цих перетворень складаються за модулем 2 з усіма іншими 32-х бітними словами вхідного блока даних, формуючи входи в першу (верхню) лінійку SL перетворень, і далі реалізується динамічне управління підстановлювальними перетвореннями, коли на вхід чергового SL перетворення надходять результати проходження блоками даних попередніх SL перетворень. Описана операція виконується два рази, тобто використовується дві лінійки SL перетворень, при цьому входами в другу лінійку SL перетворень є виходи першої лінійки SL перетворень, а виходи останніх SL перетворень кожної лінійки складаються за модулем 2 з виходами інших SL перетворень кожної лінійки, формуючи виходи циклової функції, котрі об'єднуються у два 128 бітних слова (напівблоки). Ліве вихідне 128-ми бітне слово формується як результат конкатенації чотирьох лівих 32-х бітних слів, праве 128-бітне слово - як результат конкатенації правих чотирьох 32-х бітних слів. SL-перетворення. Основними операціями функції ускладнення М-256 є SL-перетворення, які виконують обробку 32-х бітових блоків даних. Кожне вхідне 32-х бітне значення на вході SL перетворення ділиться на 4-ри байти, які замінюються відповідно до заданих таблиць байтових підстановок. У перетворенні використовується 4-ри різних таблиці, по одній для кожного з послідовних байтів. Після заміни 4-ри байти піддаються матричному множенню. Матриця перетворення є матрицею кода з максимальною відстанню (МДВ коду) та збігається з МДВ матрицею алгоритму Rijndael, але множення здійснюється з використанням іншого 1 UA 111547 C2 5 10 15 20 25 30 35 40 45 50 55 60 нерозкладного поліному. Результати матричного множення становляться 4-ма виходами SL перетворення. В схемі розгортання ключів використовують компоненти функції ускладнення для перетворення базового ключа та ключових констант у підключі шифрування. Розвинутий в цитованій роботі підхід у своїй основі зорієнтований на використання двоетапного принципу формування циклової функції, коли на верхньому (зовнішньому) рівні перетворення використовується відома схема Лея Массея [1], а динамічне управління підстановлювальними перетвореннями виконується на нижньому рівні. В свій час, коли розроблявся цей шифр, автори порахували таку двоетапну процедуру перемішування бітів даних більш ефективною з точки зору забезпечення високого рівня криптографічної стійкості шифру. Проведені до теперішнього дня дослідження [4-2, 5-3], однак, показали, що введений зовнішній рівень перемішування циклової функції виявляється якби зайвим. Циклове перетворення нижнього рівня виявляється цілком самодостатнім для реалізації граничних показників динаміки переходу шифру до стану випадкової підстановки. Однак для цього треба було подбати про те, щоб при активізації S-блоків циклової функції завжди здійснювалася активізація самого лівого (першого) SL перетворення, що задає подальшу активізацію всіх інших S-блоків. Справа в тому, що при додатковому аналізі перетворення М-256 (також як і інших перетворень нижнього рівня М-128і М-64), вдалося виявити слабкість шифрів серії "Мухомор", яка полягала в тому, що активізація S-блоків першого циклу здійснювалася цими перетвореннями нерівномірно. Якщо при активізації найлівішої четвірки байтів вхідного блока даних у функції ускладнення М-256 активізувалися всі наступні SL перетворення циклової функції, то сама права четвірка байтів входу активізувала тільки одне саме праве SL перетворення, яке потім активізувало всі 32-а S-блоки другого шару перемішування циклової функції (повторюваний шар SL перетворень). Інші ж четвірки байтів входу активізували тільки частини S-блоків першого рівня SL перетворень у відповідності з позиціями четвірок у вхідному блоці даних. Крім того, сама функція ускладнення представлялася декілька обтяженою через практичне повторення в ній однакових (ідентичних з точністю до етапу введення циклового підключа) перетворень і включала два ідентичних шари (циклів) нелінійних замін. Нарешті, деякі перетворення циклової функції вийшли такими, що дублювали одне одного. Технічною задачею винаходу є розробка способу криптографічного перетворення двійкових даних, що має більш високі показники стійкості і швидкодії. На фіг. 1 представлена структурна схема першого циклу шифру. В таблиці 1 наведені результати експерименту по визначенню кількості активних S-блоків в процентах у першому циклі шифру з використанням SL перетворень з множенням на МДВ матрицю при активізації одного байта входу в процентах. В таблиці 2 наведені розрахунки числа переходів різного типу в 48-и рядках диференціальної таблиці випадкової підстановки. В таблиці 3 наведені розрахунки числа переходів різного типу в 70-ти рядках лінійної апроксимаційної таблиці випадкової підстановки. На фіг. 2 представлена схема побудування першого циклу. В таблиці 4 наведені розрахунки показників статистичної безпеки ШУП-а. ШУП використовує у своїй конструкції принципи побудови нижнього рівня шифру "Мухомор512", тобто схема Лея Массея на верхньому (зовнішньому) рівні перетворення відкидається, і основою шифру береться 256 бітна конструкція функції ускладнення М-256. Ця циклова функція реалізує ідею управління поточними входами SL перетворень сумами за модулем 2 вхідних блоків даних з результатами виконання SL перетворень попередніх блоків даних. Шифр, названий нами "Шифром управляемых подстановок" (ШУП), забезпечує шифрування блоків даних розміром 256-ти бітів (шифр допускає масштабування, тобто можна побудувати за таким способом і 128-бітний шифр і 64-бітний або 512 бітний шифр з різними варіантами довжин майстра-ключа). Число циклів шифрування дорівнює 8-ми. Довжина майстра-ключа використовується 256 або 512 біт. При розробці цього рішення в основу були покладені наступні критерії: 1) шифр повинен приходити до випадкової підстановки за число циклів менше, ніж у відомих шифрів. 2) прихід до стану випадкової підстановки позначає, що зміна будь-якого біта входу приводить в середньому до зміни половини бітів виходу. 3) конструкція циклової функції повинна певною мірою бути простою і прозорою. 4) обчислювальна складність виконання операцій зашифрування і розшифрування повинна бути вище, ніж у відомих конструкцій шифрів з таким же розміром бітового входу. 5) шифр повинен підтримувати 32-ох бітну або 64-ох бітну платформи. 2 UA 111547 C2 5 10 15 20 25 30 35 40 45 50 55 60 6) шифр повинен дозволяти здійснювати конвеєрну обробку даних. 7) схема розгортання ключів повинна бути простою і швидкодіючою. Основна вимога для цієї схеми відсутність самоподібності циклових підключів. Ці технічні ефекти досягаються тим, що в способі шифрування двійкових блоків даних, який складається з виконання за допомогою набору підключів, сформованих з майстра-ключа, ітеративної 8-ми циклової процедури криптографічних перетворень, що включає розбивку блока даних на вході кожного циклу на вісім рівних 32-ох бітних підблоків, кожний з яких складається 32 за модулем 2 з відповідною часткою чергового циклового підключа, що подається на вхід циклової функції, і далі отримані 32-ох бітні слова подаються на перші виходи суматорів за модулем 2, підключених до шару SL перетворень, на входи яких подаються послідовно виходи попередніх SL перетворень, які підсумовуються за модулем 2 з послідовними підблоками, 32 отриманими після підсумовування за модулем 2 з відповідними частками чергового циклового підключа, при цьому вихід останнього SL перетворення подається на вихід циклової функції безпосередньо, а виходи інших SL перетворень подаються на виходи циклової функції після складання за модулем два з виходом останнього SL перетворення, а само SL перетворення при цьому будується за допомогою паралельного включення 4-ох байтових S-блоків, виходи котрих обробляються за допомогою множення на МДВ матрицю розміром 4×4, формуючи вихід SL перетворення, згідно з винаходом, в першому цикловому перетворенні для 32-ох бітної платформи усі 32-ох бітні входи циклової функції після додавання з частками циклового підключа додатково підсумовуються за модулем 2 на вході першого SL перетворення, а для 64ох бітної платформи вхідний блок даних (256-ти бітів) на вході першого циклу розбивається на 64 чотири рівних 64-ох бітних підблоків, кожний з яких складається за модулем 2 з відповідною часткою чергового циклового підключа, що подається на вхід циклової функції, a SL перетворення будуються на основі обробки 64-ох бітних блоків даних вісьма байтовими Sблоками з подальшим множенням результатів проходження S-блоків на МДВ матриці розміром 8×8, формуючи виходи SL перетворень, а наступні сім циклів при цьому повторюють циклову функцію першого циклу за винятком того, що в цих циклах відсутнє сумування за модулем 2 підблоків даних на вході першого SL перетворення, а також підсумування за модулем 2 виходу останнього SL перетворення з виходами інших SL перетворень, після цього виконується підсумування за модулем 2 виходу останнього SL перетворення восьмого циклу з виходами інших SL перетворень цього циклу і остаточне підсумування результату з останнім цикловим підключем за модулем 2, при цьому процедура розгортання майстра-ключа включає його поділ на окремі байти з подальшим виконанням циклічного зсуву майстра-ключа на числа бітів, що задаються значеннями послідовності суміжних (сусідніх) байтів і отримані циклічні зрушення майстра-ключа використовуються послідовно як чергові циклові підключі. Перерахована сукупність істотних ознак дозволяє реалізувати початкове циклове перетворення, що має поліпшені перемішуючі та розсіюючі властивостями і за рахунок цього скоротити число циклів шифрування без зниження показників криптографічної стійкості. Зменшене число циклів шифрування, очевидно, приводить і до підвищення швидкодії шифру. Нижче суть пропонованого рішення більш детально викладається з посиланнями на прикладені фігури та таблиці. Узагальнена схема запропонованого способу шифрування представлена структурою першого циклу перетворень, зображеною для 32-ох бітної платформи на фіг. 1. Кожне з 32-бітових вхідних значень функції циклового перетворення складається за 32 модулем 2 з відповідною частиною підключа, поданого на вхід функції. Всі отримані результати підсумовуються на вході першого SL перетворення за модулем 2 (це нововведення), а також надходять роздільно на суматори за модулем 2 на входах усіх інших SL перетворень. Наступні операції пояснює фіг. 1. Решта сім циклів повторюють схему фіг. 1 за винятком того, що в цих циклах відсутнє підсумовування за модулем 2 підблоків даних на вході першого SL перетворення, а також підсумовування за модулем 2 виходу останнього SL перетворення з виходами інших SL перетворень, після цього виконується підсумовування за модулем 2 виходу останнього SL перетворення восьмого циклу з виходами інших SL перетворень цього циклу і остаточне підсумовування результату з останнім цикловим підключем за модулем 2. 1 Процедура за шифрування. На вхід процедури подається відкритий текст і підключі шифрування. Отриманий блок даних задану кількість разів (8-м) обробляється цикловими функціями, і в завершенні виконується підсумовування за модулем 2 виходу останнього SL перетворення восьмого циклу з виходами інших SL перетворень цього циклу і остаточне підсумовування результату з останнім (9-им) цикловим підключем за модулем 2. Отриманий в результаті блок даних є шифр-текстом. 3 UA 111547 C2 5 10 15 20 25 30 35 40 45 50 55 60 1.1 Циклове перетворення. Вважаючи, що рішення з побудови шифру повинно мати певну елегантність і простоту при побудові циклової функції ШУП з базової конструкції шифру Мухомор було виключено ряд підсумовувань результатів проходження SL перетворень з наступними і попередніми блоками даних, тому що вони дублювали операції, реалізовані послідовністю SL перетворень. збережено лише додавання результатів проходження останнього SL перетворення з виходами інших SL перетворень, щоб забезпечити при формуванні виходу циклової функції ефекту проходження кожним байтом входу всіх SL перетворень (отримати максимально можливу кількість активних S-блоків) для кожної четвірки байтів входу. Особливу увагу при побудові циклового перетворення шифру було приділено конструкції першого циклу. Тут було поставлено завдання побудувати його так, щоб була забезпечена активізація вхідними блоками даних (колонками) одночасно і збалансовано всіх S-блоків цих цикловій функції. У результаті для 32-ох бітної платформи як циклове перетворення використовується декілька змінена функція ускладнення М-256 шифру "Мухомор". По перше, цикл ШУП практично включає тільки першу (верхню) половину перетворення функції ускладнення М-256. Практично один цикл функції ускладнення М-256 шифру "Мухомор" розбивається на два цикли (до другої частини функції ускладнення додається в самому початку складання з цикловим підключем, аналогічно операції введення циклового підключа у верхній частині циклової функції, і з одного циклового перетворення функції М-256 виходить два циклових перетворення ШУП-а. По друге, крім зазначених вище винятків ряду підсумовувань для забезпечення активізації будь-яким 32-х бітним словом входу першого SL перетворення в лінійці динамічно керованих переходів інших SL перетворень, в першому циклі після операції складання з цикловими підключами (за 32 модулем 2 ) перед заходом в SL перетворення вводиться додаткове додавання за модулем 2 (XOR) усіх 4-ох байтових сегментів вхідних блоків даних на вході першого SL перетворення. Ця операція є принциповою і має сенс тільки для вибраного способу запуску SL перетворень, де SL перетворення включені у ланцюжок з послідовним запуском один одного. Для інших (відомих) конструкцій шифрів ця процедура не має сенсу, тому що в інших шифрах S-блоки в циклову функцію входять незалежно один від одного або незалежними групами. Наступні сім циклів при цьому повторюють циклову функцію першого циклу за винятком того, що в цих циклах відсутнє підсумовування за модулем 2 підблоків даних на вході першого SL перетворення, а також підсумування за модулем 2 виходу останнього SL перетворення з виходами інших SL перетворень, після цього виконується підсумовування за модулем 2 виходу останнього SL перетворення восьмого циклу з виходами інших SL перетворень цього циклу і остаточне підсумовування результату з останнім цикловим підключем за модулем 2. Для 64-ох бітної платформи вхідний блок даних (256-ти бітів) на вході першого циклу 64 розбивається на чотири рівних 64-ох бітних підблоків, кожний з яких складається за модулем 2 з відповідною часткою чергового циклового підключа, що подається на вхід циклової функції. І в цьому випадку перед заходом в SL перетворення вводиться додаткове додавання за модулем 2 (XOR) усіх 8-й байтових сегментів вхідних блоків даних на вході першого SL перетворення. Наступні сім циклів при цьому, як і в попередньому випадку, повторюють циклову функцію першого циклу за винятком того, що в цих циклах відсутнє підсумовування за модулем 2 підблоків даних на вході першого SL перетворення, а також підсумовування за модулем 2 виходу останнього SL перетворення з виходами інших SL перетворень, після цього виконується підсумовування за модулем 2 виходу останнього SL перетворення восьмого циклу з виходами інших SL перетворень цього циклу і остаточне підсумовування результату з останнім цикловим підключем за модулем 2. 1.2 SL перетворення. Основним перетворенням циклової функції є SL перетворення, що для 32-ох бітної платформи виконує перетворення 32-бітових блоків даних. Схема SL перетворення повторює конструкцію SL перетворення шифру Мухомор (що подібна перетворенню, задіяному у шифрі Rijndael), тобто будується за допомогою 4-ох паралельно включених байтових S-блоків, виходи котрих обробляються за допомогою множення на МДВ матрицю розміром 4×4, формуючи вихід SL перетворення. Таблиці підстановок алгоритму ШУП повторюють таблиці підстановок шифру "Мухомор". Вихідним значенням SL-перетворення, як випливає з фіг. 2, є 32-бітовий вектор (слово). Для 64-ох бітної платформи SL перетворення будується на основі обробки 64-ох бітних блоків даних вісьма байтовими S-блоками з подальшим множенням результатів проходження Sблоків на МДВ матрицю розміром 8×8, формуючи вихід SL перетворення. 2. Процедура розшифрування. 4 UA 111547 C2 5 10 15 20 25 30 35 Алгоритм розшифрування є зворотним до алгоритму зашифрування. На вхід алгоритму подаються блоки зашифрованого тексту і підключі зашифрування. На самому початку процедури розшифрування здійснюється зняття фінальної рандомізації шифр-тексту, після чого з отриманого блока даних за допомогою підсумовувань за модулем 2 його відповідних підблоків формується блок даних на виході восьмого циклу шифрування, після чого отриманий блок даних необхідну кількість разів (вісім) обробляється у зворотному порядку цикловими функціями. Отриманий блок даних є блоком відкритого тексту. Залишається відзначити, що при розшифруванні - у зворотному порядку також подаються підключі розшифрування; - виконується інверсне лінійне перетворення (виконується множення на обернену МДВ матрицю);. - в якості підстановок використовуються інверсні S-блоки. 3. Процедура розгортання ключів У шифрі "Мухомор" використовується складна схема розгортання майстра-ключа. У нашому шифрі було використане більш просте рішення. При його формуванні була поставлена задача забезпечити відсутність періодичності в побудові циклових підключів. Використовується майстер ключ, в якому використовується неповторювальна послідовність байтів. Сама процедура розгортання майстра-ключа включає його поділ на окремі байти з наступним виконанням циклічного зсуву майстра-ключа на величини, що задаються значеннями суміжних (сусідніх) байтів. Якщо узятий байт повторює попередній, то використовується наступний байт. Отримані циклічні зрушення майстер-ключа і використовуються послідовно як чергові підключі. У цьому випадку для формування всього набору циклових підключів буде потрібно дев'ять послідовних байтів. Вибір байтів для розгортання ключів може стати додатковим секретним параметром шифру ( C9  225 варіантів вибору байтів). Для ключа довжиною 512 біт значенням 32 байта можна задавати число біт, які відкидаються (з початку) від майстра-ключа. Поточний підключ визначається 256-ма бітами, що йдуть після відкинутих (у цьому випадку C9  235 ). 64 4. Показники випадковості ШУП-у У цьому розділі наводяться результати оцінки очікуваних параметрів переходу ШУП до стану випадкової підстановки. У відповідності з ідеєю розвинутого в [3] підході необхідно виконати оцінку мінімального числа активних (задіяних S-блоків), після проходження яких шифр стає випадковою підстановкою. Це мінімальне число визначається диференціальними та лінійними показниками самих S-блоків, застосованих у шифрі, конструкціями і властивостями його циклових перетворень, а також значеннями показників доказовою стійкості шифру, що залежать від розміру його бітового входу. В роботі [3] цей зв'язок між зазначеними показниками визначений у вигляді двох співвідношень:    IPSD  (DPmax )k ,IPSL  2k 1  LPmax 40 45 50 55  . (1) k   Тут DPmax і LPmax - максимальні значення диференціальної і лінійної ймовірностей підстановлювальних перетворень ( x ) . IPSD (Indicator of Provable Security Differential) диференціальний показник доказовою безпеки і IPSL (Indicator of Provable Security Linear) лінійний показник доказової безпеки, k  kmin - мінімальне число активних S-блоків, що беруть участь у формуванні переходу шифру до випадкової підстановки. Користуючись розрахунковими зі співвідношеннями, встановленими в роботі [4], можна прийти до висновку, що очікуване значення максимуму диференціального переходу для шифру з 256 бітним входом виявляється близьким до 190, а очікуване значення максимуму зміщення 130 лінійного корпусу для шифру з 256 бітним входом виявляється близьким до 2 . Відповідно отримаємо, що максимальні значення лінійної та диференціальної ймовірності для шифру з 256 бітним входом виходять близькими один до одного і рівними приблизно 2248  2250 (близькими до складності атаки повного перебору ключів). Виходячи з наведених вище співвідношень, можна зробити висновок, що для шифру з 256 бітним входом потрібно для приходу до стану випадкової підстановки з диференціальних переходів при використанні S-блоків з граничними показниками -рівномірності рівними  DPmax  26 , (відповідно до рівності 2248  (26 )k ) kmin  41 S-блок (для "рідних" S-блоків з  показником -рівномірності рівними DPmax  25 маємо kmin  50 ). Аналогічно, для приходу до стану випадкової підстановки за лінійним показників при  використанні S-блоків з граничними показниками нелінійності рівними LPmax  26 буде потрібно 5 UA 111547 C2   k  ( 2 250  2k 1  2 6 ) kmin  50 S-блоків (для "рідних" S-блоків з показником нелінійності LPmax  25 5 10 15 20 25 30 35 маємо kmin  62,5 ). Оцінимо число активних S-блоків шифру на двох перших циклах шифрування. Для шифру з SL перетворенням з використанням множення на МДВ матрицю з великою ймовірністю SL перетворенням буде давати одразу 4-ри активних S-блоки. Але вихід останнього SL перетворення надходить і на виходи (сума за модулем 2) усіх попередніх SL перетворень. Вихід останнього SL перетворення, як випливає з фіг. 1, надходить і на виходи (сума за модулем 2 усіх попередніх SL перетворень. В результаті у формуванні кожного виходу циклової функції для будь-якої четвірки байтів входу буде задіяне 8+1=9 SL перетворень. Отже виходить, що кожний вхідний 32-х бітний блок даних проходить у кращому випадку за перший цикл 36 S-блоків. Що важливе, конструкція циклової функції підвищує число S-блоків, що беруть участь в формуванні вихідного ефекту циклового перетворення (замість 32-ох Sблоків байти вхідного блоку даних проходять через 36 S-блоків). Реальний стан тут пояснює таблиця 2. Видно, що з імовірністю, близькою до 0,9999 у першому циклі ШУП-у активізується 32 чи 31 S-блок (без врахування підсумувань за модулем 2 виходу останнього SL перетворення з виходами усіх попередніх SL перетворень). 64-ох бітна платформа. Оцінити властивості SL перетворень у цьому випадку можна за таким способом. Для SL перетворень з множенням на МДВ матрицю розміром 8×8 відповідно з підходами, розглянутому вище, виходить що кожний вхідний 64-х бітний блок даних проходить у кращому випадку за перший цикл 8×5=40 S-блоків. Другий цикл в кращому випадку дає 8×4=32 S-блоки. Отже за два цикли з перевищенням отримаємо 40+32=72 S-блоки. 5. Використання випадкових S-блоків Оцінимо перспективи використання в ШУП-і випадкових S-блоків. Методика виконання розрахунків представлена в роботі [5]. У табл. 3 наведені результати розрахунків числа переходів різного типу в 48-ми рядках диференціальної таблиці випадкової підстановки. Ми в своїх розрахунках скористалися відразу таким числом активних S-блоків, яке дозволяє реалізувати прихід шифру до випадкової підстановки. Для диференціальних показників воно дорівнює 48. Реальні розрахунки, що дозволяють отримати це число наведені нижче. З представлених результатів випливає, що для 48 активних S-блоків при виборі в рядках максимально ймовірних переходів можна очікувати при випадкових входах в S-блоки: - два переходи зі значенням 10; - двадцять переходів із значенням 8; - двадцять п'ять переходів із значенням 6. Всього 48 переходів (48 активних S-блоків). Обчислення в цьому випадку призводять до потрібного результату: 2  10   8       256   256  40 45 50 55 20  6     256  26  2250 . Це означає, що випадкові S-блоки для цього шифру теж забезпечують за два цикли його прихід до стану випадкової підстановки. Наведемо тепер розподіл переходів для зміщень лінійної апроксимаційної таблиці. У загальне число переходів тут входять і позитивні, і негативні зміщення. Користуючись результатами роботи [5], можемо розрахувати числа переходів різного типу в 70 рядках лінійної апроксимаційної таблиці випадкової підстановки, підсумки розрахунків яких представлені в табл. 4. Знову будемо вважати, що за рахунок введення циклових підключів входи в S-блоки будуть випадковими і статистично незалежними. Методика розрахунків представлена в роботі [5]. У таблиці наведені результати оцінки числа переходів і їх значень у 70 випадково взятих рядках таблиці ЛАТ. З результатів випливає, що для 70 активних S-блоків при використанні максимально ймовірних переходів можна очікувати при випадкових входах у випадковий Sблок: один перехід зі значенням 32; три переходу зі значенням 30; вісім переходів зі значенням 28; вісімнадцять переходів зі значенням 26; тридцять дев'ять переходів зі значенням 24. Найперший (один) S-блок узятий з максимально можливим значенням переходу (34). Вважаючи далі, що рядки в S-блок вибираються з усієї множини з 256-ти рядків, при цьому переходи по S-блоках йдуть в довільному порядку і здійснюються за найбільш ймовірним шляхом, можемо виконати оцінку ймовірності приходу шифру до стану випадкової підстановки з випадковими S-блоками. Обчислення для значення k  70 призводять до результату 6 UA 111547 C2 2 69 2 5 10 15 20 25 30 35 40 45 50 55  34   32       128   128  2   30      128   2 3 8 18 2 2       28      26          128     128          24 2        128     39  2257 і, отже, 70 активних S-блоків дозволяють здійснити перехід шифру до випадкової підстановки за два цикли. Нагадаємо на закінчення, що шифр Rijndael приходить до стану випадкової підстановки з диференціальних показників на третьому циклі, а по лінійних показниках лише на четвертому. 6. Показники обчислювальної складності. Як і в роботі [6], при оцінці обчислювальної складності будемо орієнтуватися на число XOR операцій, виконуваних шифром в процесі зашифрування і розшифрування. Будемо виходити з того, що для виконання SL перетворення у вигляді матричного множення, як у шифрі Rijndael, потрібно виконати 4-ри XOR операції [6]. Отже у першому циклі ШУП-у буде використано 8×4+3×7=53 XOR-и. В інших циклах буде використано по 32 XOR-и у кожному циклі. В результаті у восьми циклах буде задіяне 53+32×7+8=285 XOR-ів, тобто ШУП повинен бути помітно більш швидким, ніж AES. Нагадаємо, що у AES-256 на 14-ть циклів припадає 32×14=448-м XOR-ів. Але тут ще не враховуються витрати на процедуру розгортання майстра-ключа. У нашому випадку процедура розгортання ключа буде набагато більш швидкою, ніж у інших шифрах, в тому числі швидше, ніж в шифри AES і Мухомор. Зауважимо, що шифр "Мухомор-256" буде повільнішим (більш ніж у два рази) в порівнянні з шифром ШУП і забезпечуватиме перехід до стану випадкової підстановки на двох циклах за диференціальними показниками (60-т S-блоків). За лінійним характеристиками необхідно три цикли (80 активних S-блоків). Природно, що в цьому випадку для трьох циклів і випадкові Sблоки призводять до показників випадкової постановки. Наведемо, нарешті результати експериментальної оцінки обчислювальної складності ШУП Застосовувався процесор Intel Core iS-750, 2,7 GHz (зашифрування здійснювалось одним потоком). Оперативна пам'ять 6 Гб. Отримані такі характеристики швидкодії ШУП-а: ШУП (8 циклів, довжина ключа шифрування 256 бітів), реалізація без оптимізації: - зашифрування:  11,9 Мбайт/с; - розшифрування:  10,9 Мбайт/с. ШУП (14 циклів, довжина ключа шифрування 256 бітів), реалізація без оптимізації: - зашифрування:  6,64 Мбайт/с; - розшифрування:  5,64 Мбайт/с. Для порівняння наведемо дані по швидкодії для шифрів Rijndael і Калині (теж не оптимізовані версії) у тих же самих умовах. Шифр Rijndael (14-ть циклів, ключ і блок по 256ти бітів): - зашифрування:  5,17 Мбайт/с. Оптимізована версія AES (14 циклів, ключ 256 бітів, блок 128 бітів): - зашифрування:  248 Мбайт/с. Для блока довжиною 256 бітів результат для шифру AES буде майже у два рази меншим. Зауважимо, що запропонована версія блочного симетричного шифру теж може бути оптимізована, тобто можна очікувати швидкодію оптимізованої версії шифру ШУП більше 200 Мбайт/с (мова йде про 256 бітну конструкцію). 7. Конвеєрна обробка даних. Циклові функції, котрі використовуються в обох шифрах на останніх семи циклах допускають конвеєрну обробку даних. Дійсно після формування виходу першого SL перетворення другого циклу можна одразу ж з формуванням виходу другого SL перетворення даного циклу формувати вихід першого SL перетворення третього циклу. Після формування виходу другого SL перетворення другого циклу можна одразу ж з формуванням виходу другого SL перетворення третього циклу формувати і вихід першого SL перетворення четвертого циклу і т.д. Якщо рахувати, що для 32-ох бітної платформи для виконання операції SL перетворення потрібно затратити час Т, то для окремої лінійки (циклу) з m SL перетворень потрібно буде потратити mТ сек. При конвеєрній обробці кожний черговий s-тий цикл буде починатися з затримкою у (s-1)T c, 1  s  r. В результаті, якщо для обробки r циклів при зашифруванні одним потоком буде потрібно витратити rm сек, то при паралельній обробці r циклів достатньо буде витратити m  r  1 сек. Отже виграш у швидкодії, котрий може бути досягнутий складає: 7 UA 111547 C2 - Якщо шифр будується з використанням 32-ох бітної платформи, то для r  7, m  8 маємо виграш у швидкодії обчислення семи останніх циклів зашифрування у рази. - Для 5 14-ти циклового шифру маємо виграш конвеєрної 15 20 25 30 35 40 45 50 55 обробки, що складає 14  8 112   5,3 разів. 14  8  1 21 - Для шифру на 64-ох бітній платформі r  7, m  4 маємо виграш у 10 mr 78 56   4 m  r  1 7  8  1 14 mr 74 28    2,8 m  r  1 7  4  1 10 разів (майже в три рази). Таким чином, описаний шифр, названий авторами ШУП-ом, представляється авторами як найбільш перспективне рішення з побудови сучасних шифрів. Він має найкращі з відомих шифрів динамічні показники приходу до випадкової підстановки. Практично він стає випадковою підстановкою вже з другого циклу, чого не дозволяє жоден з відомих шифрів, що означає його підвищену стійкість до атак диференціального та лінійного криптоаналізу (дозволяє зменшити кількість циклів зашифрування). За іншими показниками стійкості цей шифр успадкував всі високі показники, властиві шифру "Мухомор" [7]. Зауважимо також важливу особливість шифру, яка полягає в тому, що в шифрі практично без зниження показників стійкості можуть застосовуватися випадкові S-блоки. За показниками обчислювальної складності шифр працює істотно швидше AES-a. Важливою особливістю шифру є те, що він допускає конвеєрну обробку блоків даних, при цьому відкривається можливість подальшого збільшення його швидкодії від 3-ох до 5-ти разів. Зупинимося більш детально на оцінці стійкості запропонованого рішення по побудові процедури шифрування до відомих методів криптоаналізу. Стійкість до лінійного і диференціального криптоаналізу. Відносно підвищеної стійкості до відомих методів криптоаналізу, і, зокрема до лінійного і диференціального криптоаналізу можна відзначити, що за рахунок використання механізму керованої підстановки реально слід очікувати відсутності будь-яких статистично стійких асиметричних (зміщених по ймовірності) зв'язків між входами і виходами циклових перетворень і всього шифру в цілому. Очевидно, що результуючі показники доказової стійкості для шифру ШУП збігаються з показниками стійкості відомих шифрів AES, Калина та інші. Підвищення стійкості в даному випадку означає, що ШУП становиться випадковою підстановкою вже на другому циклі. Існуюча практика побудування шифрів встановила правило, відповідно до якого число циклів шифрування береться у 3-4 рази збільшеним відносно числа циклів шифру потрібних для його виходу до стану випадкової підстановки. Отже в нашому випадку число циклів шифрування ШУП вибрано рівним 8-ми, тобто вважається що шифр буде забезпечувати гарантовано граничні показники стійкості до атак лінійного та диференціального криптоаналізу при 8-ми циклах шифрування. Це і дозволяє підвищувати показники обчислювальної складності в запропонованих рішеннях. Інтегральна атака. Інтегральна атака застосовується до шифрів з добре збудованою структурою, подібною структурі SPN. Так як запропонована циклова функція відрізняється від тих, що звичайно застосовуються в SPN конструкціях наявністю недетермінованого механізму управління підстановками, то видається, що навряд чи вдасться знайти інтегральний розрізнювач для цілої структури всього шифру. Інші атаки. Статистичні атаки. Враховуючи високі дифузійні властивості циклової функції, високий ступінь нелінійності S блокового перетворення і "достатність" числа циклів, можна з упевненістю сказати, що пропоновані рішення будуть стійкими до всіх варіантів лінійного та диференційного криптоаналізу та їх поєднань, до бумерангових і rectangle атакам і їх узагальненням, подібним атакам з використанням зрізаних диференціалів і диференціалів високого порядку, неможливих диференціалів і багатьом іншим атакам. Відносно-ключова і слайд атаки. Слайд атаки експлуатують періодичні структуру алгоритму розгортання ключів. Пропоноване рішення по формуванню циклових підключів виключає їх подібність.. Інтерполяційні і алгебраїчні атаки. Інтерполяційні атаки використовують переваги Sблокового представлення, а саме його просту алгебраїчну структуру. Представляється, що, сам недетермінований механізм, реалізований за допомогою керованих підстановок, навряд чи може знайти аналітичний опис (на наш погляд вимоги до відбору підстановок у запропонованих рішеннях можуть виявитися істотно більш м'якими, ніж, наприклад, в шифрі FOX). Тому видається, що відмічені атаки не є скільки-небудь ефективними для запропонованих рішень. 8 UA 111547 C2 5 10 15 20 25 30 35 40 45 Запропонований спосіб може бути реалізований за допомогою пристроїв, з'єднання між якими ілюструє блок-схема на фіг. 2. Шифр починається з нетривіального циклу, представленого для 32-ох бітової платформи на фіг 2, де 1 - блок формування 32-х бітних сегментів даних на вході циклової функції, 2 - регістр-накопичувач циклового підключа, 3 блоки 32 підсумовування 32-бітних сегментів з сегментами циклового підключа за модулем 2 , 4 багатовходовий суматор за модулем 2, 5 - блоки керованих SL перетворень, 6 - суматори за модулем 2, 7 - накопичувач-формувач перетвореного блока даних. Реалізація запропонованого способу не викликає труднощів, оскільки всі блоки і вузли, які входять в пристрій, що реалізує спосіб, загальновідомі і широко описані в технічній літературі. Далі наведені деякі результати експериментальної оцінки показників статистичної безпеки пропонованої процедури. В табл. 4 представлені результати аналізу лавинного ефекту, реалізованого в експериментах з нашим шифром. Наводяться числа одиничних і нульових елементів в побітових різницях зашифрованих блоків на виході кожного циклу для пар блоків даних на вході шифру, що відрізняються одним бітом, а також показники ступеня повноти dc, ступеня лавинного ефекту da та ступеня суворого лавинного критерію dsa [2]. З таблиці 4 видно, що у всіх випадках змінюється половина біт зашифрованого тексту з відхиленням ±0,21, що відповідає 0,008 %. Видно також, що відхилення відбувається в обидві сторони. Отримані результати свідчать, що показники лавинного ефекту (глибина входу в цикли шифру і дисперсія відхилень від середнього значення) краще за всіх відомих криптографічних алгоритмів [2]. Практично вже на першому циклі ШУП становиться випадковою підстановкою по всіх показниках. Результати аналізу існуючих перетворень в цілому показують, що використання недетермінованих процедур криптографічних перетворень і, зокрема, процедур керованих підстановок, дозволяє уникнути багатьох слабостей фіксованих детермінованих перетворень. Джерела інформації: 1. X. Lai. A proposal for a new block encryption standard. / X. Lai and J. Massey.// In I. Damg°ard, editor, Advances in Cryptology-EUROCRYPT'90, volume 473 of Lecture Notes in Computer Science, pages 389-404. Springer-Verlag, 1991. 2. Долгов Виктор Иванович. Методология оценки стойкости блочных симметричных шифров к атакам дифференциального и линейного криптоанализа: монография. / В.И. Долгов, И.В. Лисицкая. - Харьков. Издательство "Форт", - 2013. - 420 с. 3. Gorbenko I.D. On Ciphers Coming to a Stationary State of Random Substitution /I.D. Gorbenko, K.E. Lisitskiy, D.S. Denisov // Copyright © 2013 Horizon Research Publishing. 4. Lisitskiy K.E. On Maxima Distribution of Full Differentials and Linear Hulls of Block Symmetric Ciphers [Text] / K.E. Lisitskiy // I J. Computer Network and Information Security, 2014, 1, 11-18 Published Online November 2013 in MECS (http://www.mecs-press.org/) DOI: 10.5815/ijcnis. 2014.01.02. 5. Горбенко И.Д. О динамике прихода шифров к случайной подстановке при использовании S-блоков с показателями нелинейности близкими к предельным / И.Д. Горбенко, К.Е. Лисицкий // Радиотехника: Всеукр. межвед. Науч.-техн. сб. - 2014. - Вып. № 176. - С. 276. Горбенко И.Д. Свойства и возможности оптимизации криптографических преобразований в AES-RIJNDAEL / И.Д. Горбенко, Д.А. Чекалин // Радиотехника. Всеукр. Межвед. Науч.-техн. сб. 2001. Вып 119. С. 36-42. 7. Бондаренко М.Ф. Обґрунтування вимог та розробка основних рішень з побудування та властивості перспективного БСШ "Мухомор" / М.Ф. Бондаренко, І.Д. Горбенко, B.I. Долгов, Р, В. Олійников та інші // Прикладная радиоэлектроника. - Харьков: ХНУРЭ. - 2007. - Том 6, № 2. - С. 174-185. Таблиця 1 Кількість активних S-блоків 27 28 29 30 31 32 Оцінка кількості в % 0,000048 0,000811 0,031328 0,692749 10,978746 87,905693 50 9 UA 111547 C2 Таблиця 2 Значення переходу таблиці 12 10 8 6 Число переходів диференціальної таблиці 1 10 104 830 Число переходів у рядку 0,003906 0,039065 0,40625 3,24218 Число переходів у 48 рядках 0,19 1,87 19,5 155,62 Таблиця 3 Число переходів у 70 випадково взятих рядках таблиці ЛАТ 0,546 1,092 2,744 7,686 18,116 40,04 81,48 Значення переходу Число переходів у Число переходів в рядку таблиці ЛАТ таблиці ЛАТ таблиці ЛАТ ±34 ±32 ±30 ±28 ±26 ±24 ±22 1,998 4 10 28 65 146 298 0,0078 0,0156 0,0392 0,1098 0,2588 0,572 1,164 Таблиця 4 Раунд № 1 2 3 4 5 6 7 8 Mmin 127,73 127,73 127,76 127,74 127,81 127,73 127,73 127,71 Dmin 63,453 63,382 64,862 65,081 63,227 64,11 65,464 63,476 Mmax 128,21 128,2 128,19 128,22 128,22 128,2 128,26 128,22 ШУП Dmax mv 62,91 127,97 65,331 127,96 63,409 127,98 63,156 127,98 64,299 128,01 64,721 127,96 62,903 128 66,24 127,97 dc 1 1 1 1 1 1 1 1 da 0,999479 0,999482 0,999518 0,999491 0,999484 0,999497 0,999506 0,999484 dsa 0,992026 0,992 0,992047 0,992015 0,992027 0,991971 0,992003 0,992081 5 ФОРМУЛА ВИНАХОДУ 10 15 20 25 1. Спосіб шифрування двійкових блоків даних, який складається з виконання за допомогою набору підключів, сформованих з майстра-ключа, ітеративної 8-циклової процедури криптографічних перетворень, яка включає розбивку блока даних на вході кожного циклу на 32 вісім рівних 32-бітних підблоків, кожний з яких складається за модулем 2 з відповідною частиною чергового циклового підключа, що подають на вхід циклової функції, і далі отримані 32-бітні слова подають на перші виходи суматорів за модулем 2, підключених до шару SL перетворень, на другі входи яких подають послідовно виходи SL перетворень, при цьому вихід останнього SL перетворення подають на вихід циклової функції безпосередньо, а виходи інших SL перетворень подають на виходи циклової функції після складання за модулем два з виходом останнього SL перетворення, а саме SL перетворення при цьому будують за допомогою паралельного включення 4-байтових S-блоків, виходи котрих обробляють за допомогою множення на МДР матрицю розміром 4×4, формуючи вихід SL перетворення, який відрізняється тим, що для шифру, побудованому на 32-бітній платформі в першому цикловому перетворенні усі 32-бітні входи циклової функції після додавання з частками циклового підключа додатково підсумовують за модулем 2 на вході першого SL перетворення, а наступні сім циклів при цьому повторюють циклову функцію першого циклу, причому в цих циклах відсутнє підсумовування за модулем 2 підблоків даних на вході першого SL перетворення, а також підсумовування за модулем 2 виходу останнього SL перетворення з виходами інших SL перетворень, після цього виконують підсумовування за модулем 2 виходу останнього SL перетворення восьмого циклу з виходами інших SL перетворень цього циклу і остаточне 10 UA 111547 C2 5 10 15 20 25 30 підсумовування результату з останнім цикловим підключем за модулем 2, при цьому процедура розгортання майстра-ключа включає його поділ на окремі байти з подальшим виконанням циклічного зсуву майстра-ключа на числа бітів, що задають значеннями послідовності суміжних (сусідніх) байтів і отримані циклічні зрушення майстра-ключа використовують послідовно як чергові циклові підключи. 2. Спосіб шифрування двійкових блоків даних, який складається з виконання за допомогою набору підключів, сформованих з майстра-ключа, ітеративної 8-циклової процедури криптографічних перетворень, яка включає розбивку блока даних на вході кожного циклу на 32 вісім рівних 32-бітних підблоків, кожний з яких складається за модулем 2 з відповідною частиною чергового циклового підключа, що подають на вхід циклової функції, і далі отримані 32-бітні слова подають на перші виходи суматорів за модулем 2, підключених до шару SL перетворень, на другі входи яких подають послідовно виходи SL перетворень, при цьому вихід останнього SL перетворення подають на вихід циклової функції безпосередньо, а виходи інших SL перетворень подають на виходи циклової функції після складання за модулем два з виходом останнього SL перетворення, а саме SL перетворення при цьому будують за допомогою паралельного включення 4-байтових S-блоків, виходи котрих обробляють за допомогою множення на МДР матрицю розміром 4×4 формуючи вихід SL перетворення, який відрізняється тим, що для шифру, побудованому на 64-бітній платформі в першому цикловому перетворенні вхідний блок даних (256-ти бітів) на вході першого циклу розбивають на чотири 64 рівних 64-бітних підблоків, кожний з яких складається за модулем 2 з відповідною часткою чергового циклового підключа, що подають на вхід циклової функції, a SL перетворення будують на основі обробки 64-бітних блоків даних вісьма байтовими S-блоками з подальшим множенням результатів проходження S-блоків на МДВ матрицю розміром 8×8, формуючи вихід SL перетворення, а наступні сім циклів при цьому повторюють циклову функцію першого циклу, причому в цих циклах відсутнє підсумовування за модулем 2 підблоків даних на вході першого SL перетворення, а також підсумовування за модулем 2 виходу останнього SL перетворення з виходами інших SL перетворень, після цього виконують підсумовування за модулем 2 виходу останнього SL перетворення восьмого циклу з виходами інших SL перетворень цього циклу і остаточне підсумовування результату з останнім цикловим підключем за модулем 2, при цьому процедура розгортання майстра-ключа включає його поділ на окремі байти з подальшим виконанням циклічного зсуву майстра-ключа на числа бітів, що задають значеннями послідовності суміжних (сусідніх) байтів і отримані циклічні зрушення майстра-ключа використовують послідовно як чергові циклові підключі. 11 UA 111547 C2 12 UA 111547 C2 Комп’ютерна верстка Д. Шеверун Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 13