Спосіб оптимізації механічних систем

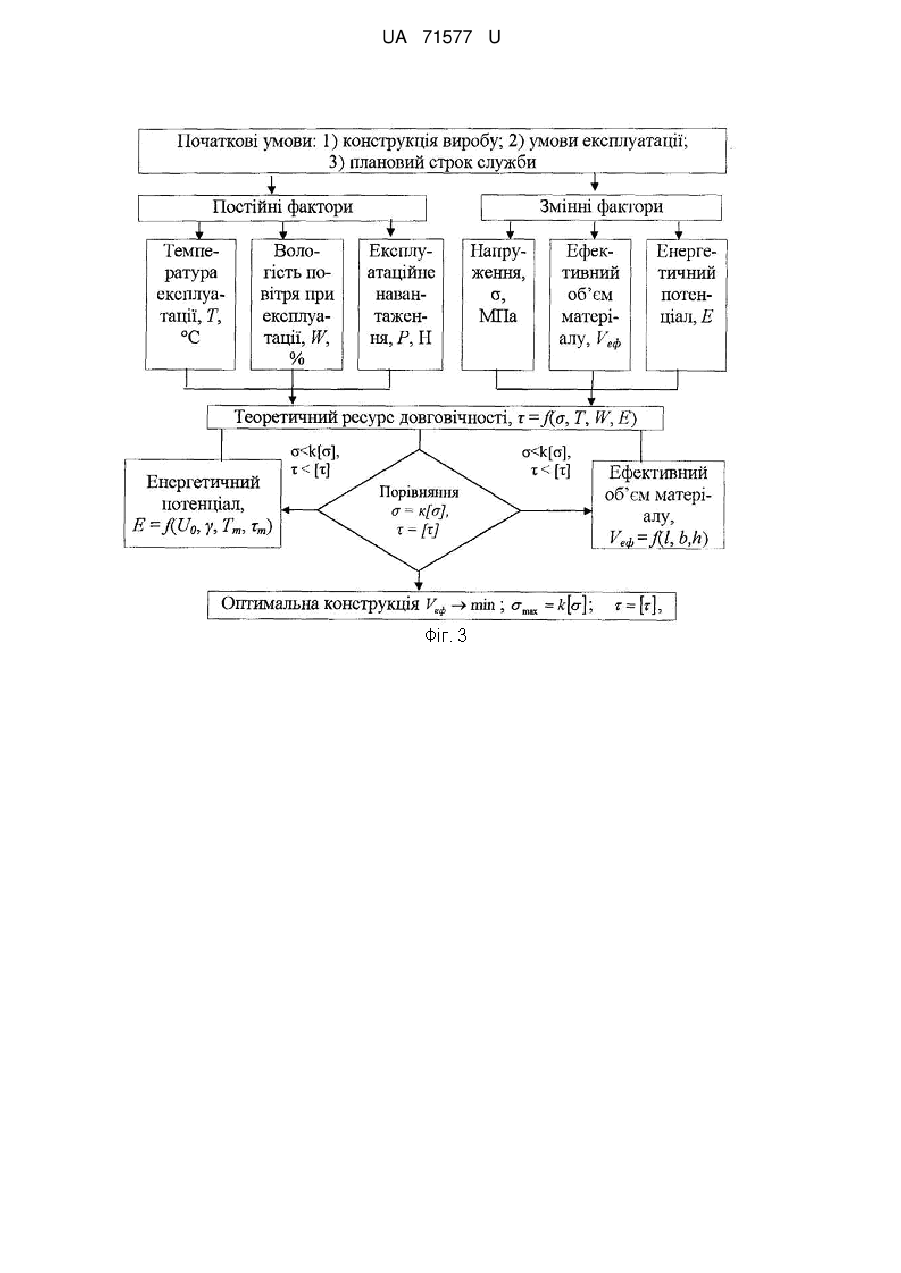
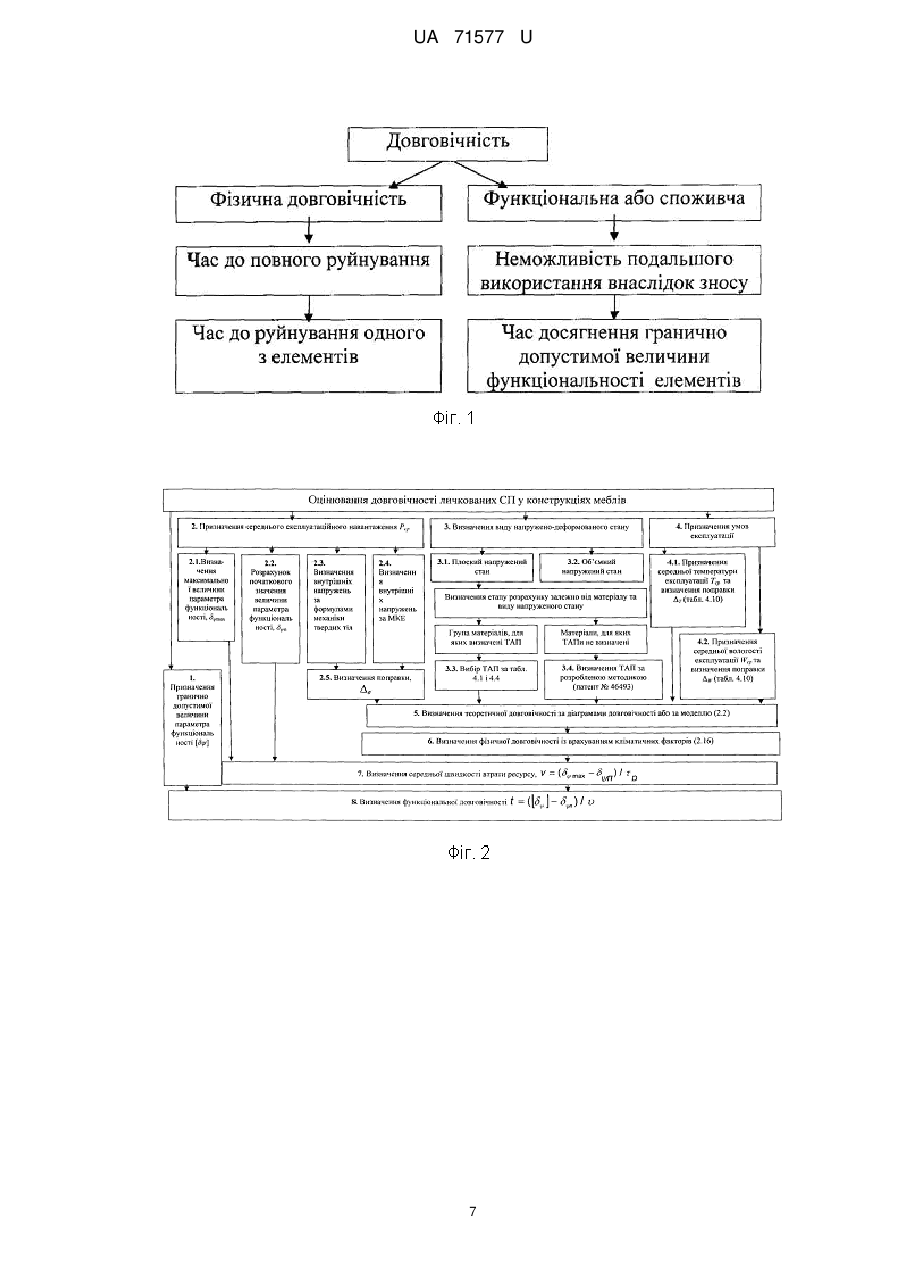
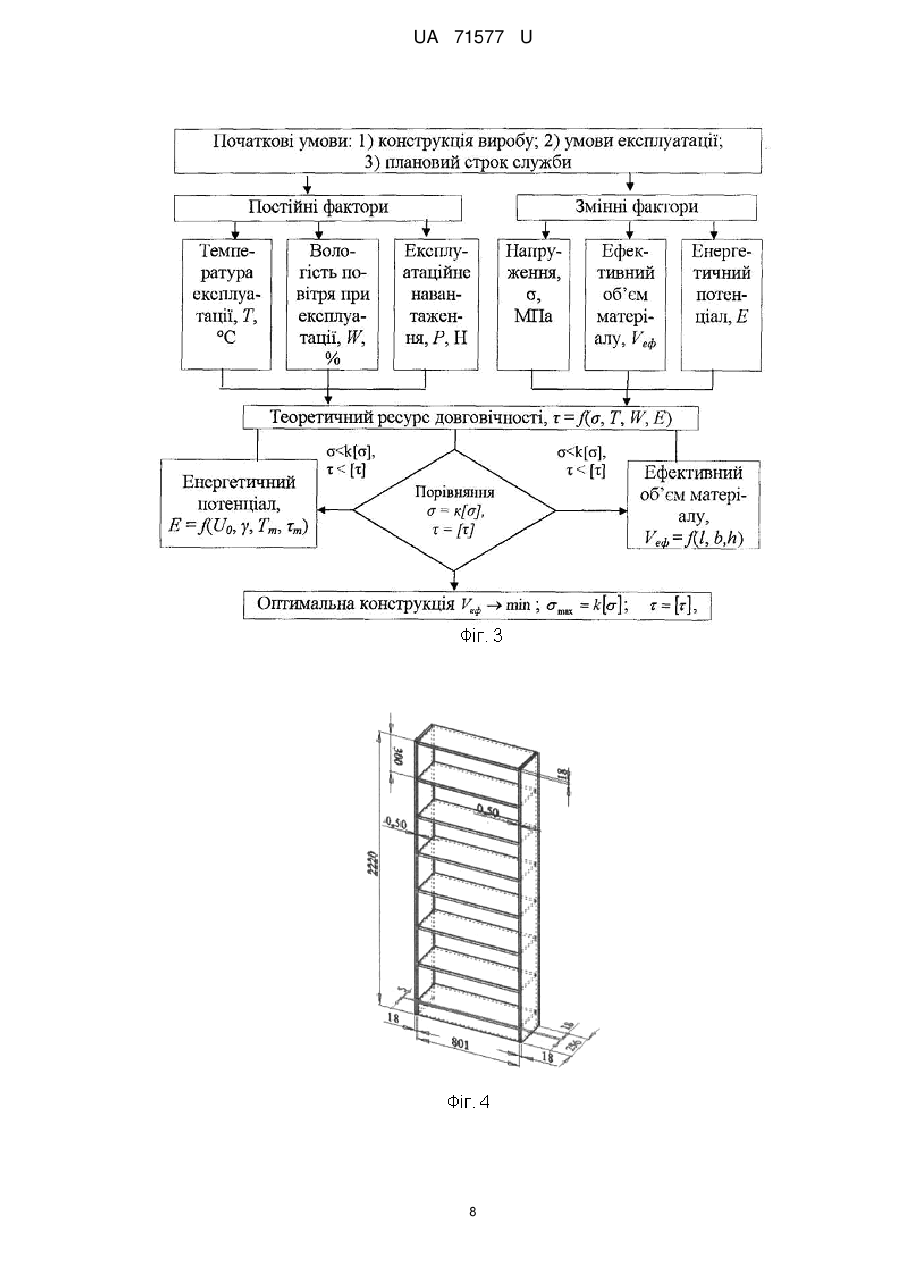
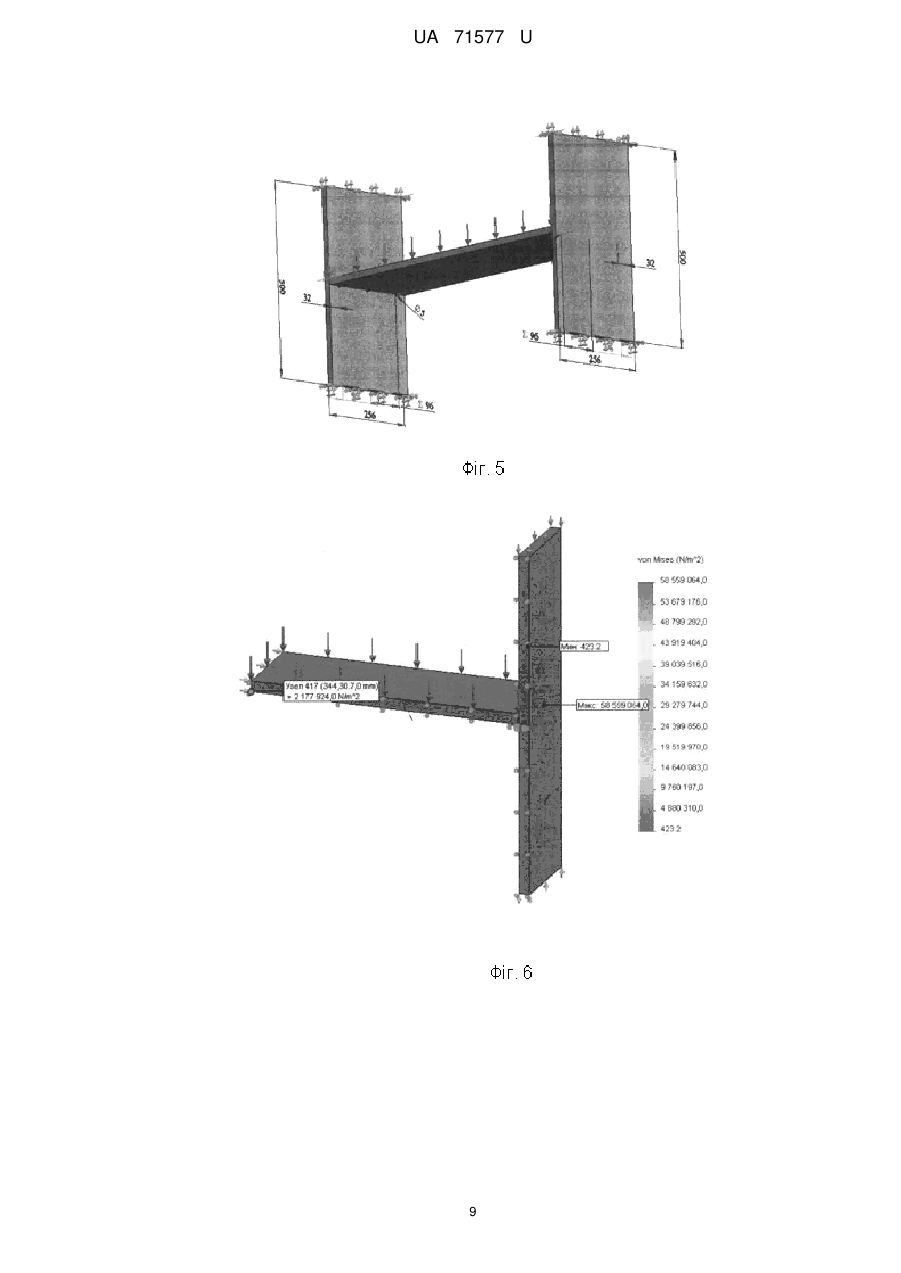
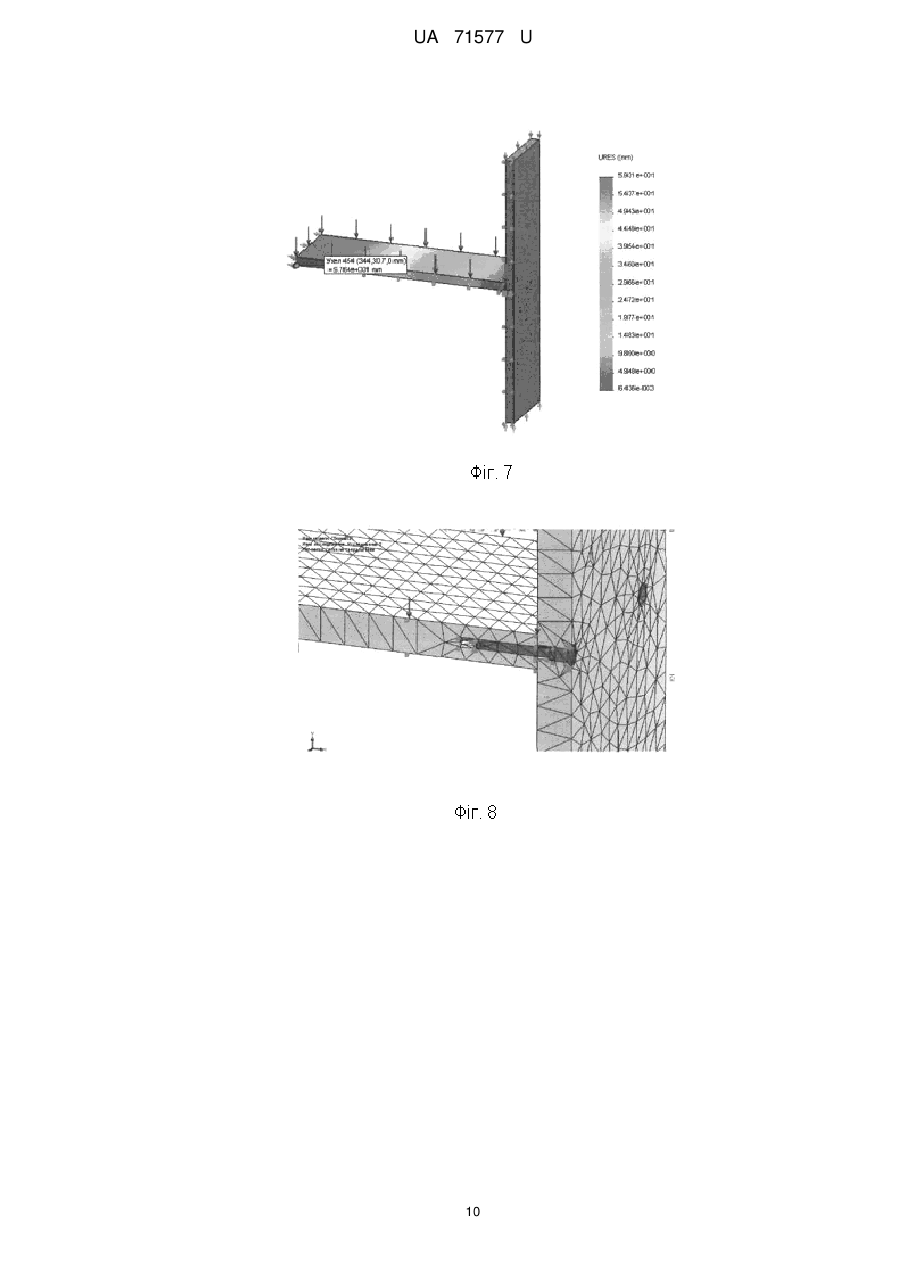
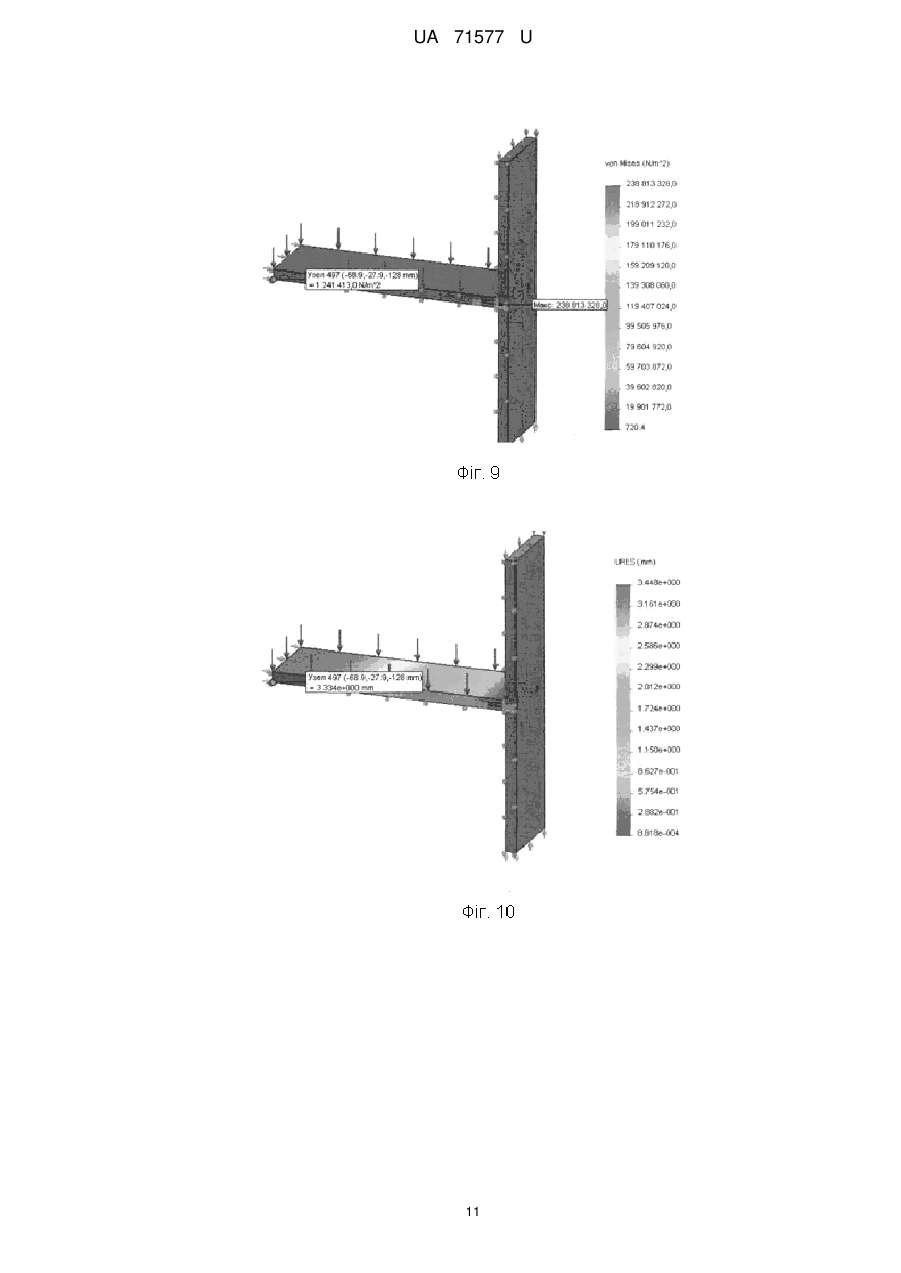
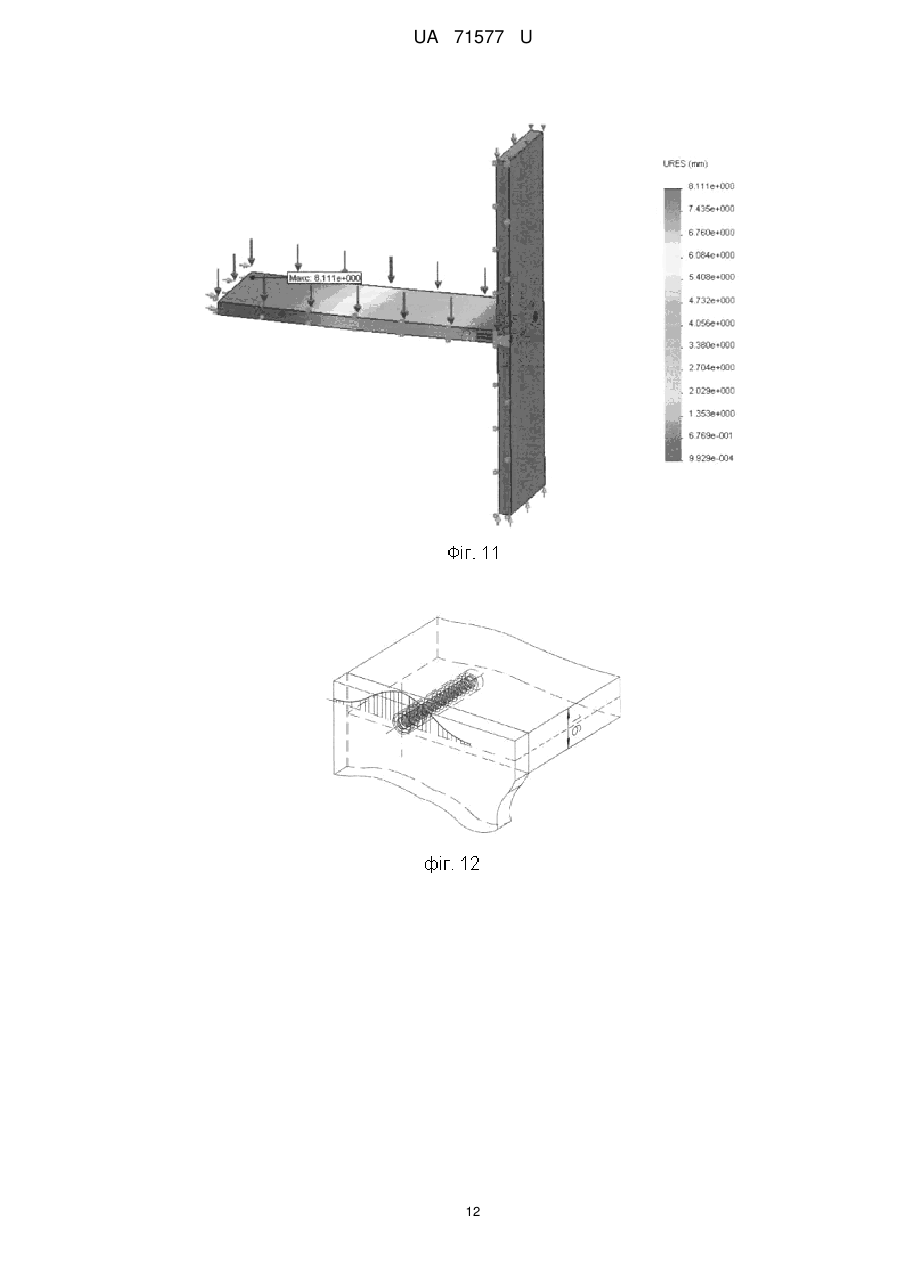
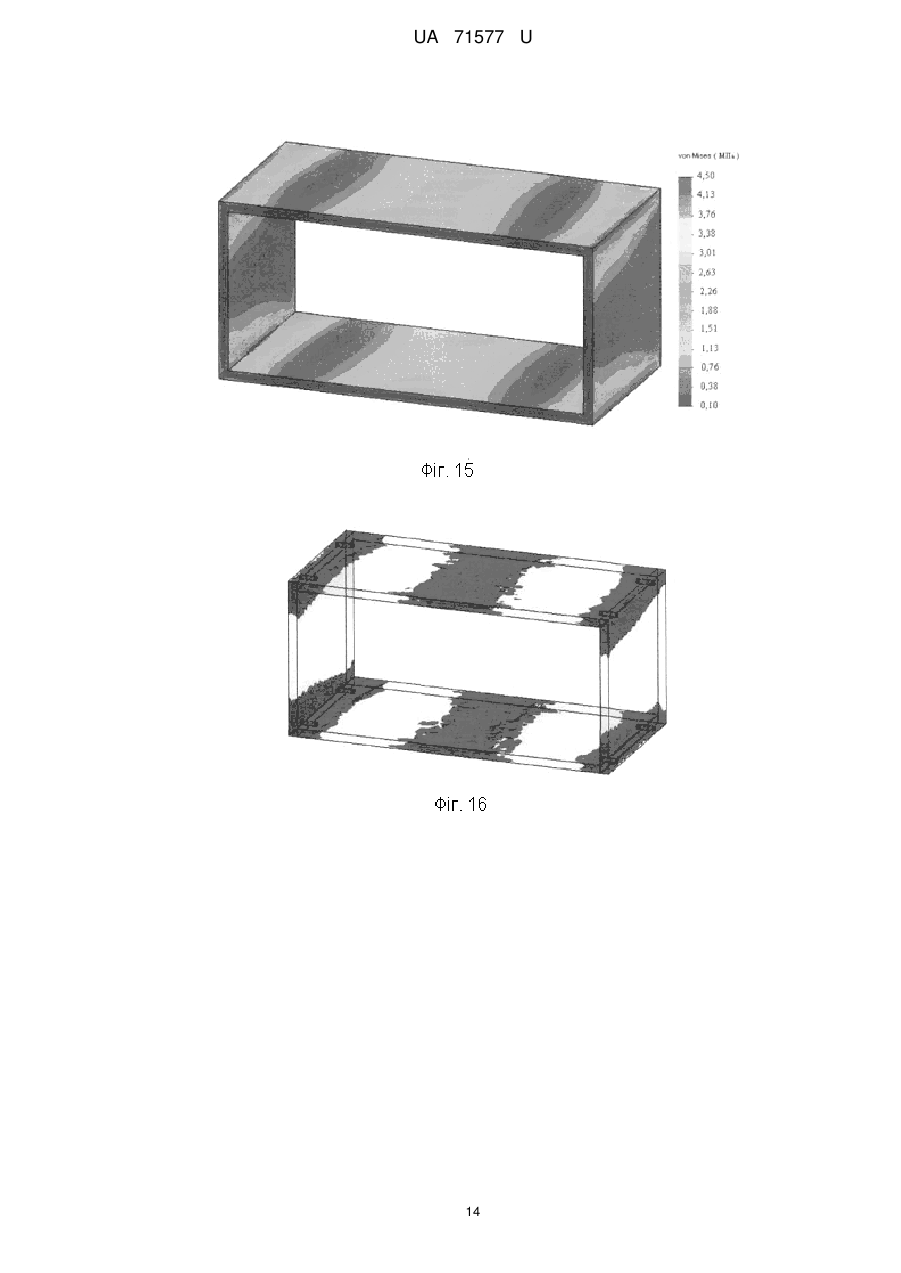
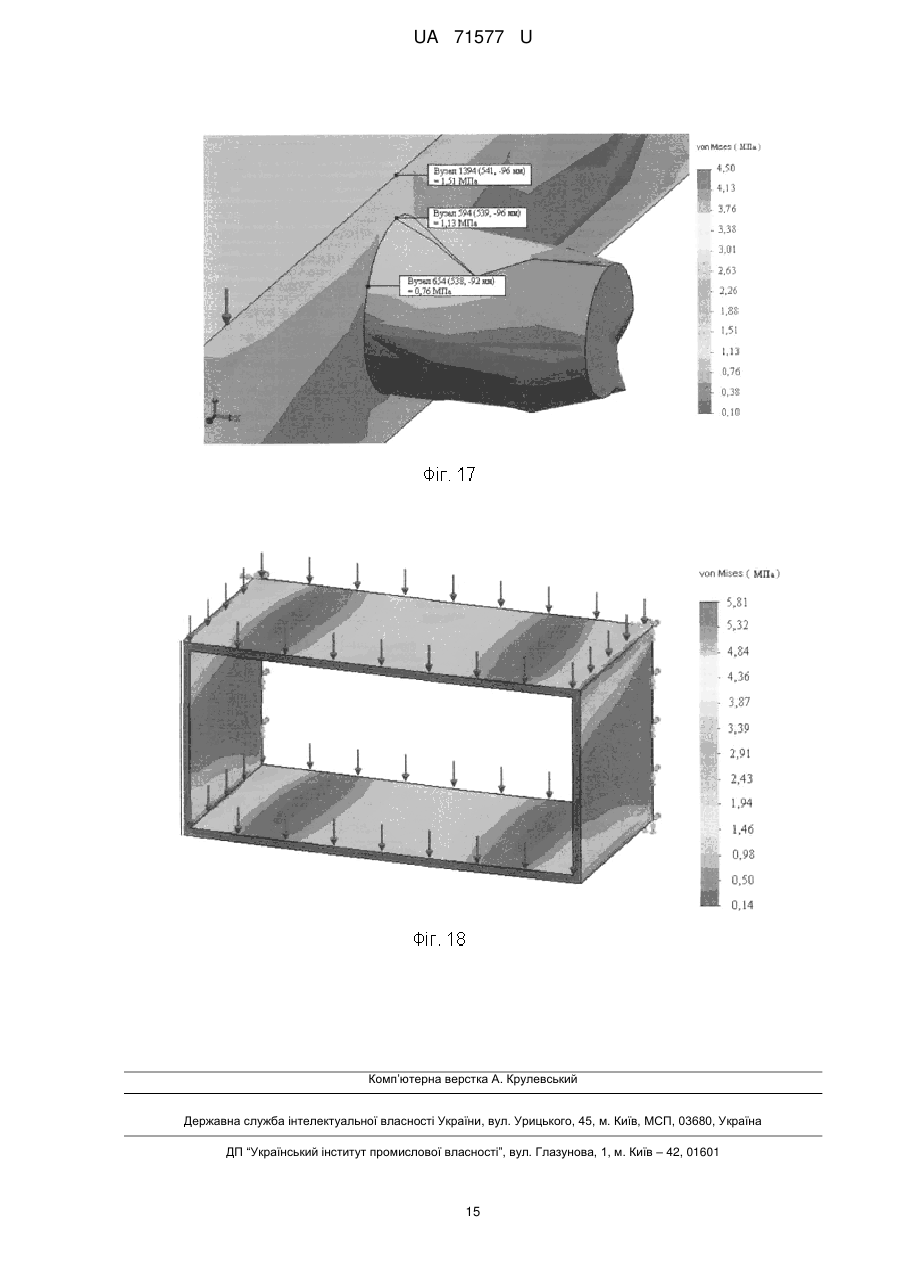
Реферат: Спосіб оптимізації механічних систем, що полягає у визначенні мінімальної маси конструкції механічної системи, здатної витримувати допустимі значення напруження під дією допустимих навантажень, причому задають плановий строк служби механічної системи,  ; визначають термоактиваційні параметри механічної системи, такі як; U0 - максимальну енергію активації руйнування, кДж/моль;  - структурно-механічний параметр, кДж/(молъ·МПа); Tm - граничну температуру існування механічної системи (температуру деструкції), К; m - мінімальну довговічність (період коливання кінетичних одиниць - атомів, груп атомів, сегментів), с; та виконують розрахунок прогнозування довговічності механічної системи. Порівнюють розрахунковий та плановий строк служби та виконують вибір оптимальної конструкції механічної системи. UA 71577 U (12) UA 71577 U UA 71577 U 5 10 15 20 25 30 35 40 45 50 55 60 Корисна модель належить до галузі оптимізації пружних механічних систем. Відомий спосіб оптимізації полягає в досягненні мінімальної маси конструкції, яка може витримувати допустимі навантаження. При цьому мета оптимізації полягає в пошуку мінімального значення функції декількох змінних, що задовольняє декільком додатковим вимогам [1]. Ця функція називається цільовою, а додатковим вимогам відповідають конструктивні обмеження. Цільова функція Z і функції обмежень f1, f2, … fn повинні бути виражені через структурні змінні X1, Х2, … Хn: Z=Z (X1, X2, … Хn), f1-f1 (X1, Х2, … Хn), f2=f2 (X1, X2, … Хn), fn=fn (X1, X2, … Хn). У пружних системах, що працюють на розтяг-стиск, структурні змінні - це, як правило, площі поперечних перерізів або їх розміри, а цільова функція - маса системи Z: Z =∑ρі∙Li∙bi∙hi, де pi - щільність матеріалу, Li - довжина, bi - ширина, hi - товщина деталі. Через площі перерізів або розміри повинні бути виражені і функції обмежень. Незалежними змінними при оптимізації будуть розміри деталей. Як обмеження найчастіше використовуються: допустимі значення напруг; допускаються переміщення в певних точках конструкції; зусилля або напруги втрати стійкості; розміри перерізів [1]. Проте використання даного способу, призводить часом до суперечливих результатів оптимізації, оскільки він не враховує впливу допустимих навантажень на довговічність проектованих механічних систем. І оптимальна з точки зору міцнісних властивостей механічна система протягом часу свого існування веде себе непередбачуваним чином. Тобто може зруйнуватися в саме невідповідний час. Відомий і спосіб оптимізації полягає в забезпеченні рівноміцності всіх елементів механічної системи для досягнення її мінімальної маси, яка може витримувати допустимі навантаження. Спосіб розглядає, крім вищезазначених, також безліч параметрів різної природи. Таких як геометричні (довжину, висоту, ширину, товщину, площа, координати і т.д.), фізико-механічні (модуль пружності, коефіцієнт Пуассона, коефіцієнт лінійного температурного розширення, межа плинності, твердість, щільність матеріалу, теплоємність і т.д.). Зовнішні впливи на механічну систему можуть бути описані відповідним безліччю зовнішніх впливів. Таких як розосереджені або зосереджені сили, температурні, кліматичні дії, інтенсивність опромінення і т.д. Крім того, спосіб розглядає такі параметри, як умови експлуатації (коефіцієнт запасу міцності, жорсткості, стійкості і т.п.). Величини коефіцієнтів безпеки конструкції відображають багатоневраховані фактори в фізичній моделі, наближене завдання експлуатаційних навантажень, наближеність методів аналізу стану системи і т.п. Критерій ефективності або цільова функція може бути при цьому виражена кількісним показником. Зокрема їм може бути показник ваги конструкції, вартість, надійність і т.п. Цільова функція повинна задовольняти певним обмеженням параметрів. Працездатною (допустимою) вважається при цьому така система, для якої виконуються умови неприпустимості перевищення цих обмежень. Як обмеження приймаються: обмеження на напружений стан; обмеження на деформований стан; обмеження на умови місцевої стійкості; обмеження на умови загальної стійкості системи; обмеження на частоти власних коливань; обмеження на амплітуди механічних коливань; обмеження на швидкість руху деформівної системи; обмеження на параметри [2]. Однак цей спосіб не бере до уваги зміну стану матеріалів, з яких складаються механічні системи, в часі. І тому не дозволяє спрогнозувати, як буде вести себе спроектована за цим способом оптимальна конструкція в часі. В основу корисної моделі поставлено задачу удосконалення способу оптимізації механічних систем з тим, щоб мати можливість на етапі їх оптимізації знати їхні потенційні можливості. При цьому технічний результат полягає в підвищенні точності та достовірності прогнозування довговічності оптимальної механічної системи. Поставлена задача вирішується тим, що у відомому способі оптимізації механічних систем, що полягає в досягненні, наприклад, мінімальної маси конструкції, здатної витримувати допустимі значення напруг, як додаткове обмеження використовується мінімально допустима довговічності механічної системи. За основу способу прогнозування прийнята теорія термофлуктуаційного руйнування твердих тіл, що полягає в дослідженні впливу не лише величини і тривалості прикладеного навантаження, але і температури експлуатації виробів, на їх довговічність. При цьому використовуються рівняння, що відображають фізичні закономірності. Згідно з кінетичною концепцією, міцність руйнування твердого тіла розглядається не як критична подія, а 1 UA 71577 U 5 10 15 20 як поступовий кінетичний, термоактиваційний процес, що розвивається в механічно напруженому тілі в часі з моменту прикладання до нього навантаження, зокрема менше критичного. На відміну від механічних уявлень, що враховують лише конкуренцію між прикладеною силою і силами міжатомних зв'язків, вона розглядає тепловий рух атомів як вирішальний чинник процесу механічного руйнування. Для руйнування матеріалу необхідний час, протягом якого в навантаженому тілі протікають процеси, що приводять до його розділення на частини. Таким чином, при будь-яких температурах механічне руйнування є таким, що відбувається в часі механотермічним процесом, що реалізується через елементарні акти розриву міжатомних (хімічних) зв'язків. Час саме по собі ролі не грає, він лише збільшує кількість теплових флуктуацій, необхідних для реалізації тих процесів розриву зв'язків, які перешкоджають критичній події. Проте ця подія може не наступити, оскільки завдяки тепловому руху розірвані зв'язки рекомбінуються. У механічному полі процес розриву зв'язків прискорюється. При цьому роль навантаження полягає в зменшенні енергії зв'язків (і відповідно енергії активації, яка їй пропорційна), зміні відстані між кінетичними одиницями, а також у фіксації їх переміщень, зокрема в утрудненні рекомбінації радикалів. Отже, спрямованість прикладеної сили забезпечує безповоротність процесу внаслідок накопичення цих розривів. Отже, головний руйнуючий чинник - це теплові флуктуації, тобто енергія руйнування тіла більшою мірою черпається із запасу теплової енергії, чим з роботи зовнішніх сил. При цьому довговічність визначається по формулі [3]:  25 30   U   1     m exp 0 T  Tm1  , (1) R   де,  - час до руйнування (довговічність), с; m , U0 ,  і Tm - фізичні константи, які визначаються по результатах проведення випробовування; m - мінімальна довговічність (період коливання кінетичних одиниць - атомів, груп атомів, сегментів) (при T  Tm ), с; U0 - максимальна енергія активації руйнування, кДж/моль;  - структурно-механічна константа, кДж/(мольхМПа); Tm - гранична температура існування твердого тіла (температура деструкції), К; R - універсальна газова стала, кДж/(мольхК); 35 40 45 50 55  - напруження, МПа; T - температура, К. Приклад використання способу оптимізації механічних систем застосуємо при оптимізації меблевих конструкцій. Відомо, що довговічність може розглядатися у двох аспектах: фізична довговічність та споживча або функціональна довговічність. Перша - обмежується часом до її повного руйнування або руйнування одного з найбільш важливих елементів. Друга - функціональна довговічність, характеризує час, протягом якого меблі зберігають свої функціональні, споживчі якості (Фіг. 1). Прогнозування функціональної довговічності полягає у визначенні часу, протягом якого формозмінність функціонально важливого параметра, наприклад прогину книжкової полиці, призведе до неможливості або незручності використання даного виробу, тобто до досягнення гранично допустимої величини функціональності. Методика оцінки довговічності личкованих стружкових плит у конструкціях корпусних меблів може бути подана у вигляді алгоритма (Фіг. 2), який складається із наступних етапів: 1. Призначення гранично допустимої величини параметра функціональності [ψ]. Для цього використовують відповідні стандарти, технічні умови тощо на певний виріб. 2. Призначають середнє навантаження Рср. та визначають поправки  за діаграмою ∆f(). 2.1. Визначення гранично допустимої величини параметра функціональності ψmax, виходячи із умов втрати міцності в момент руйнування. 2.2. Розрахунок початкового значення величини параметра функціональності ψ шляхом визначення величини абсолютно пружної деформації ψпр. 2 UA 71577 U або 5 10 15 20 25 30 35 40 45 50 55 2.3 Визначення величини внутрішніх напружень вн за формулами механіки твердого тіла, 2.4. визначення величини внутрішніх напружень вн за методом МКЕ. 2.5. Визначення поправки ∆ за діаграми ∆f(). 2. Визначення виду напружено-деформованого стану: плоский або об'ємний напружений стан. Залежно від матеріалу і виду напруженого стану при умові, що група матеріалів, вже досліджена, то: 3.3 термоактиваційні параметри (ТАП) можна вибрати за довідником; якщо ТАПи для даного матеріалу не визначені, то їх можна: 3.4. дослідити, користуючись методом, згідно з патентом України № 46493 (Спосіб прогнозування довговічності кутових з'єднань корпусних меблів). 3. Призначення умов експлуатації. 4.1. Призначення середньої температури експлуатації T ср та визначення поправки ∆T за діаграмою ∆f(T). 4.2. Призначення середньої вологості експлуатації W cp і визначення поправки ∆W за діаграмою ∆f(W). 5. Визначення фізичної довговічності р з врахуванням кліматичних факторів за формулою (1). 6. Визначення середньої швидкості втрати ресурсу визначаємо за формулою: v=(ψmax-ψП)/р, (2) де v - швидкість втрати ресурсу; ψmax - максимально допустима деформація; ψn - початкова деформація (пружна деформація в момент прикладання навантаження); р - розрахункова фізична довговічності. 7. Визначення функціональної довговічності як часу, протягом якого матеріал досягне гранично допустимої величини параметра функціональності за формулою: t=(ψmax-[ψ])/v, (3) На сьогоднішній день меблеві вироби конструюються на основі критеріїв міцності, тобто такі, які можуть витримувати максимальне експлуатаційне навантаження. Для вибору оптимальної меблевої конструкції одного критерію міцності недостатньо, тому необхідно використовувати одночасно критерії міцності та довговічності. Необхідні дії під час пошуку оптимального розв'язання даної вибраної задачі показано у вигляді алгоритму (Фіг. 3). Під час розв'язання задачі оптимізації як цільова функція може бути прийнята мінімальна вартість виробу. При цьому працездатність виробу протягом всього планового строку служби повинна забезпечуватися мінімальним ефективним об'ємом матеріалу на його виробництво. Vеф → min, при max=k[]; =[], (4) де Vеф - ефективний об'єм матеріалу личкованої стружкової плити, що сприймає робоче навантаження; max - напруження в ефективному об'ємі; к - коефіцієнт запасу міцності; [] - допустиме напруження;  - прогнозована розрахункова довговічність; [] - планований строк служби виробу. Оцінимо довговічність книжкової шафи, що показано на фіг. 4. У даному випадку полиця відрізняється від горизонтальної стінки тим, що не є скріпленою жорстко з бічними стінками корпусу, і має можливість змінювати своє розташування в книжковій шафі. Вона зв'язана з бічними стінками за допомогою полицетримачів. Для розрахунку довговічності книжкової полиці приймемо матеріал - ламінована СП, виробництва ТОВ "Кроно-Україна". Заводські характеристики матеріалу; модуль пружності Е=2600 МПа, межа міцності на згин []=14 МПа, 3 щільність 700 кг/м . Етап 1. Як критерій споживчої довговічності приймаємо величину максимального прогину книжкової полиці. Споживча довговічність визначиться часом досягнення величини прогину полиці, що, згідно з вимогами споживчого попиту, дорівнює [ψ] =10 мм. Фізична довговічність визначиться як максимальна величина прогину в момент руйнування. Етап 2. Розподілений тиск на книжкову полицю становить q=1250 Па. Визначаємо величину внутрішніх напружень вн за МКЕ (етап 2.4) Товщина плити і габаритні розміри деталей показані на Фіг. 4. Для зменшення розмірності при розрахунках за МКЕ застосуємо принцип симетрії, який дозволяє значно знизити кількість розрахункових вузлів і пришвидшити розрахунок. 3 UA 71577 U 5 10 15 20 25 30 35 40 45 50 55 Розрахунковий вузол, що включає об'єкт дослідження (горизонтальну полицю), показаний на Фіг. 5. Результати розрахунків показано на епюрах еквівалентного напруження за Мізесом (Фіг. 6). Таким чином, на підставі проведеного комп'ютерного дослідження визначили початкове значення параметра функціональності (етап 2.2). Максимальний прогин всередині полиці склав ψп=6,8 мм, а максимальні напруження в точці максимального прогину - =2,18 МПа. Враховуючи, що межа міцності при згині полиці складає 14 МПа, дана полиця має великий запас міцності, а отже фізичну довговічність. Для аналізу споживчої довговічності визначимо, який би був прогин у полиці у випадку, коли тиск на полицю призвів до напруження, близького до межі міцності, тобто до напруження в момент руйнування. Методом послідовних наближень визначимо, що руйнування полиці відбудеться за величиною тиску q=9500 Па. При цьому максимальний прогин у момент руйнування склав ψ=57,64 мм (Фіг. 7). Отже тим самим визначили гранично допустиму величину параметра функціональності (етап 2.1). Етап 3. Полиця в корпусі шафи зв'язана з бічними стінкам за допомогою полицетримачів, тому матеріал працює у плоскому напруженому стані (етап 3.1). Для плоского напруженого стану термоактиваційні параметри для даного матеріалу є такими: U0=196 кДЖ/моль, =9,1 кДЖ/моль∙МПа, lg0=-0,7, Тm= 486 К. (етап 3.3). Етап 4. Призначаємо умови експлуатації. Температура в приміщенні змінюється від 10 °C до 25 °C. Поправка для коливання температури [6] ∆T=-0,0007T+1,0835. Середня вологість у приміщенні W=60 % поправка: ∆w=-0,0015W+1,09. Етап 5. Теоретична довговічність полиці, при даній схемі навантаження, що розрахована за формулою (1), складе близько р=962 років. Етап 6. Фізична довговічність з врахуванням умов експлуатації =р/∆∑=962/1,08=890 років, де     W   T     1,07  1,0  1,09  1,08 . Етап 7. Середня швидкість втрати ресурсу довговічності книжкової полиці визначаємо за формулою (2). Для нашого прикладу. v=(57,64-6,8)/890=0,057 мм/рік. Етап 8. Визначення функціональної довговічності як часу, протягом якого матеріал досягне гранично допустимої величини параметра функціональності за формулою (3). Для нашого прикладу: t=(10-6,8)/0,057=56 років. Для порівняння впливу конструкції кутового з'єднання на довговічність скористаємося прикладом, який показаний на Фіг. 8, за умови кріплення полиці за допомогою конферматів, замість полицетримачів. На відміну від попередньої конструкції конфермат виконує одночасно функцію стягування та полицетримання. Решта параметрів, включаючи значення прогину полиці, що визначає функціональну довговічність [ψ]=10 мм, залишаться тими, що і у попередньому прикладі. Оцінку довговічності визначаємо за тим же алгоритмом. Етап 1. Як критерій споживчої довговічності приймаємо той же критерій, допустимий прогин полиці [ψ]=10 мм. Розподілений тиск на книжкову полицю становить q=1250 Па. Визначаємо величину внутрішніх напружень вн за МКЕ (етап 2.4). Товщина плити і габаритні розміри деталей показані на Фіг. 5. 6. Для зменшення розмірності при розрахунках за МКЕ застосуємо принцип симетрії. Розрахунковий вузол, що включає горизонтальну полицю, показано на Фіг. 8. Епюра еквівалентного напруження у системі полиця-конфермат-стінка показана на Фіг. 9. Напруження в точці вимірювання =1,24 МПа, значення прогину в цій точці показано на Фіг. 10 і дорівнює ψn=3,33 мм. При цьому максимальне напруження у системі, яка досліджується, виникає у конферматі і дорівнює мах=238,8 МПа. На Фіг 10. показана епюра переміщень досліджуваної системи, що дає можливість визначити початковий прогин полиці. Для аналізу довговічності визначимо, який би був прогин полиці у випадку, коли тиск на неї викликає напруження, близьке до межі міцності, тобто у момент руйнування. Методом послідовних наближень знайдемо, що руйнування полиці відбудеться при значенні тиску q=3000 Па. При цьому максимальний прогин складе ψmax=28,11 мм (Фіг. 11). З Фіг. 11 видно, що максимальні напруження виникають в області конфермата. Полиця зв'язана з корпусом за допомогою конферматів, тому СП у зоні конферматів знаходиться в об'ємному складному напруженому стані. 4 UA 71577 U 5 10 15 20 25 30 35 40 45 50 55 Дослідження величини максимального напруження max у зоні контакту полиці і конфермата методом зондування показало, що матеріал у цій зоні працює на межі працездатності. Значення напруження у зоні ймовірної втрати працездатності показано на Фіг. 13. На Фіг. 12 відображено епюру максимальних напружень у полиці, що проходить через вісь конфермата. Етап 3. Термоактиваційні параметри для кутового меблевого з'єднання на конферматах наступні: U0=262 кДЖ/моль, =15,7 кДЖ/моль∙МПа, lgm=-0,75, Тm=437 К (етап 3.3). Етап 4. Призначаємо умови експлуатації. Температура в приміщенні змінюється від 10 °C до 25 °C. Поправка для коливання температури ∆T=-0,0018T+1,1359. Середня вологість в приміщенні W=60 %, поправка: ∆w=-0,002W+1,135. Етап 5. Теоретична довговічність полиці при даній схемі навантаження розрахована за формулою (1) і буде слугувати до її повного руйнування близько 196,6 років. Етап 6. Фізична довговічність з врахуванням умов експлуатації =р/∆Σ=197/1,086=181 років, де     W   T     1,104  1,015  1,05  1,086 . Етап 7. Середня швидкість втрати ресурсу довговічності книжкової полиці визначали за формулою (2): v=(28,11-3,3)/181=0,14 мм/рік. Етап 8. Визначення функціональної довговічності як часу, протягом якого матеріал досягне гранично допустимої величини параметра функціональності, визначали за формулою (3) і дорівнює t=(10-3,3)/0,14=47 років. Таким чином, через 47 років книжкова полиця за даного навантаження буде мати прогин, що є максимально допустимий, виходячи зі споживчих вимог. Отже, можна зробити порівняння результатів, отриманих у разі дослідження залежності працездатності полиці від виду кріплення її у конструкції шафи, а саме використання конфермата, для кутового меблевого з'єднання призводить до появи додаткового концентратора напруження. Це, у свою чергу, має вирішальне значення для працездатності всієї системи. У разі використання рівняння (1) можна побудувати математичну модель довговічності книжкової полиці, яка знаходиться у складному напруженому стані. Приклад вирішення зворотної задачі оптимізації. Проект модульної системи складається із п'яти елементів, за допомогою яких можна скомпонувати до сорока компоновок різного дизайну та функціонального призначення. Дизайн-проект показано на Фіг. 14. Початкові умови: 1) геометрична модель виробу згідно з дизайн-проектом (Фіг. 14). Матеріал для виготовлення меблів: ламінована стружкова плита, що має термоактиваційні параметри: U0=260 кДЖ/моль, =15,6 кДЖ/моль∙МПа, m=-0,72, Тm=443 К; товщина матеріалу h≤[h]=16 мм; допустиме напруження []=14 МПа. 2) Експлуатація виробу планується в нестаціонарних умовах. Навантаження на полицю q=1250 Па; середня температура експлуатації 25 °C; вологість повітря 60 %. 3) Планований строк служби виробу []=30 років. За об'єкт дослідження прийнята секція максимальних габаритів. Для розрахунку напружень застосовуємо МКЕ. Для першого варіанта розрахунку приймемо, що товщина ламінованої стружкової плити 16 мм, габаритні розміри секції 300(Н)х300x600 (мм), задню стінку не показано. Результати розрахунків показано на епюрах еквівалентного напруження за Мізесом (Фіг. 15), максимальні напруження складають =4,50 МПа. Зони, що найбільше навантажені в процесі експлуатації секції, показано на Фіг. 16 синім кольором. Для того, щоб уточнити розподілене навантаження в області шканта, сховаємо бічну стінку і дослідимо область крайки у місці встановлення шканта. Епюра розподілення навантаження в області шканта показана на фіг. 17. Як видно з епюри (Фіг. 17), напруження в області шканта нижче допустимого, тому в розрахунок приймаємо величину максимального еквівалентного напруження в області кріплення задньої стінки. Як видно із епюри еквівалентного напруження, максимальне значення ек=4,50 МПа, що менше допустимого, ек[]=30 і ек=4,50