Спосіб створення незалежних багатомірних градуювальних моделей

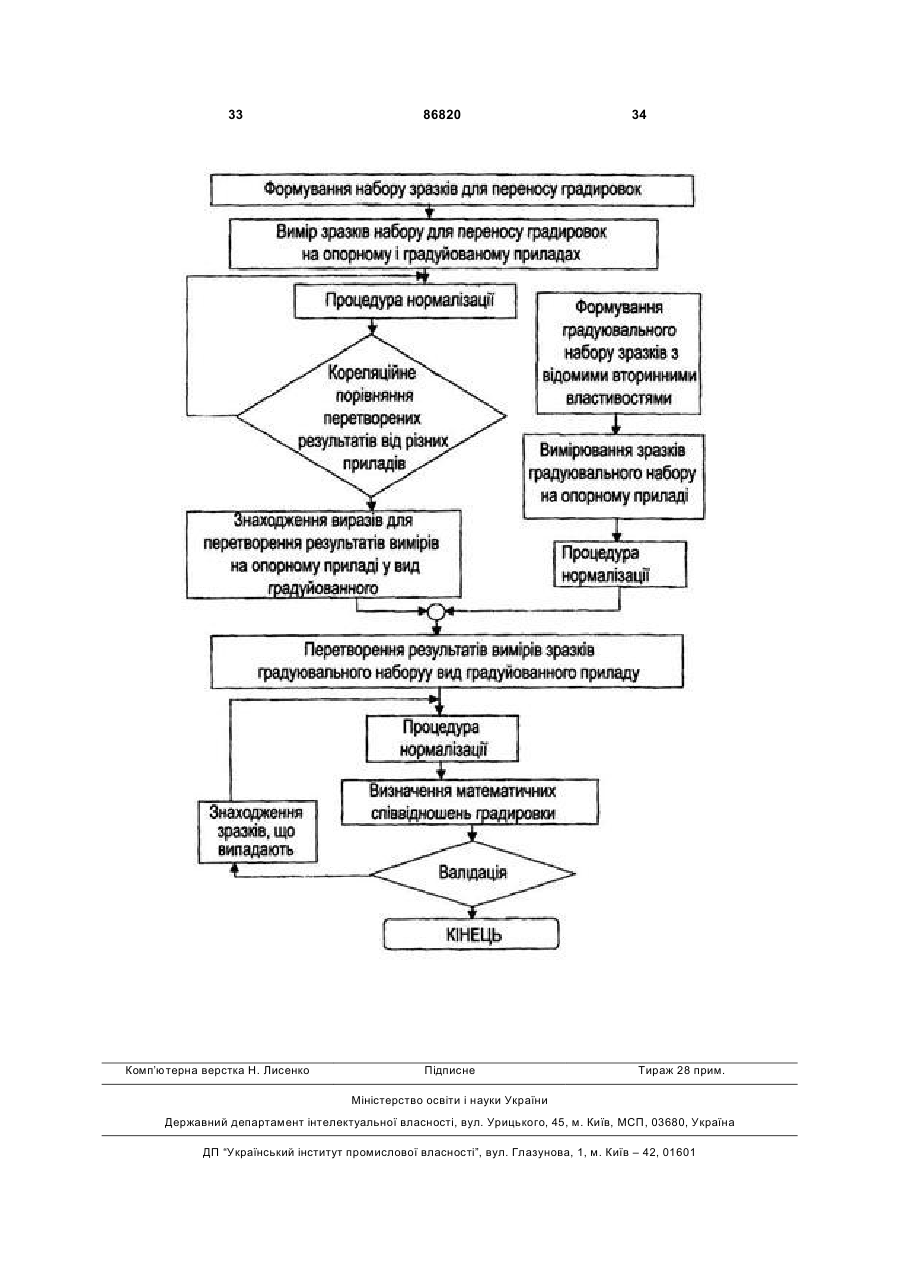
1. Спосіб створення незалежних багатомірних градуювальних моделей, що включає підбір градуювального набору зразків з відомими вторинними властивостями, вимір на опорному приладі первинних властивостей кожного із зразків градуювального набору, перетворення за допомогою співвідношень переносу градуювань результатів виміру первинних властивостей зразків градуювального набору на опорному приладі у вигляд, еквівалентний результатам виміру зразків градуювального набору на градуйованому приладі, зіставлення перетворених у вигляд, еквівалентний результатам виміру на градуйованому приладі, результатів вимірів первинних властивостей зразків градуювального набору з відомими вторинними властивостями цих зразків, і створення за допомогою методів багатомірного регресійного аналізу незалежної багатомірної градуювальної моделі, яка виражає вторинні властивості зразків через обмірювані на градуйованому приладі первинні властивості, який відрізняється тим, що математичні співвідношення переносу градуювань визначають, підбираючи набір зразків для переносу градуювань, вимірюючи первинні властивості кожного зразка з набору для переносу градуювань на 2 (19) 1 3 86820 4 градуювання виключають із градуювального набору зразки, що випадають. 6. Спосіб за п.1, який відрізняється тим, що у випадку, якщо процедура валідації градуювальної моделі показала невідповідність створеної градуювальної моделі заданим критеріям точності, результати виміру первинних властивостей зразків градуювального набору на опорному приладі, перетворені у вигляд, еквівалентний результатам виміру зразків градуювального набору на градуйованому приладі, доповнюють результатами вимірів первинних властивостей додаткових градуювальних зразків з відомими вторинними властивостями, проведеними на градуйованому приладі, і знаходять співвідношення градуювання за результатами виміру первинних властивостей зразків градуювального набору, перетвореними у вигляд, еквівалентний результатам виміру на градуйованому приладі, доповненим результатами виміру додаткових градуювальних зразків на градуйованому приладі. 7. Спосіб за п.6, який відрізняється тим, що доповнені градуювальні дані аналізують на присутність даних, що випадають, за допомогою статистики передбачення викидів, і перед визначенням співвідношень градуювання виключають із градуювального набору зразки, що випадають. 8. Спосіб за п.6, який відрізняється тим, що результати вимірів первинних властивостей зразків доповненого градуювального набору перетворюють у вигляд, еквівалентний результатам вимірів цих зразків на будь-якому іншому приладі, у тому числі на колишньому опорному приладі, після чого знаходять співвідношення градуювання і будують нову незалежну градуювальну модель, причому прилад, на якому проводилися виміри первинних властивостей додаткових градуювальних зразків, виступає як новий опорний прилад. 9. Спосіб за п.1, який відрізняється тим, що у випадку, якщо процедура валідації градуювальної моделі показала невідповідність створеної градуювальної моделі заданим критеріям точності, до визначення співвідношень градуювання перетворені у вигляд, еквівалентний результатам вимірів на градуйованому приладі, результати вимірів первинних властивостей зразків із градуювального набору і/або відповідні відомі вторинні властивості градуювальних зразків піддають процедурі нормалізації. 10. Спосіб за п.6, який відрізняється тим, що у випадку, якщо процедура валідації градуювальної моделі показала невідповідність створеної градуювальної моделі заданим критеріям точності, перед визначенням співвідношень градуювання доповнені градуювальні дані і/або відповідні відомі вторинні властивості градуювальних зразків піддають процедурі нормалізації. 11. Спосіб за п.1, який відрізняється тим, що як опорний і градуйований прилади використовують спектрометри, причому результати вимірів спектральних характеристик зразків, що описують поглинання, відбиття або розсіювання світла при різних значеннях хвильових чисел, використовують як первинні властивості зразків. 12. Спосіб за п.11, який відрізняється тим, що використовують спектрометри на основі принципу Фур'є-спектроскопії, причому перетворення результатів вимірів первинних властивостей на опорному приладі у вигляд, еквівалентний результатам вимірів на градуйованому приладі, виконують без урахування спектральних зсувів. Винахід, що заявляється, стосується аналітичного приладобудування. Зокрема, винахід стосується способів створення градуювальних моделей для різного виду вимірювальних приладів, які дозволяють визначити одну або кілька вторинних властивостей невідомого зразка за результатами виміру багатьох первинних властивостей цього зразка. У різних галузях промисловості й наукових досліджень виникає задача визначення однієї або одночасно декількох властивостей зразків, наприклад, октанового числа бензину або вмісту протеїну, вологи й золи в зерні пшениці. Причому при визначенні властивостей зразків суттєвими є такі характеристики методу виміру як швидкість проведення аналізу й збереження зразків у процесі вимірів. Це особливо важливо для промислового застосування, коли прагнуть мати швидкий контроль, що не руйнує властивостей продукції на різних стадіях виробництва. Дуже часте визначення властивостей зразка за допомогою прямих методів виміру не забезпечує необхідної швидкості аналізу або приводить до руйнування зразка. Типовим прикладом є задача аналітичної хімії по визначенню концентрацій утворюючих зразок компонентів, де традиційний прямий метод хімічного аналізу заснований на проведенні хімічних реакцій, що приводить до руйнування зразка, а, крім того, потрібний значний час для проведення аналізу. Тому для вирішення проблеми швидкого неруйнівного аналізу властивостей зразків був розроблений цілий ряд непрямих методів, де властивості зразків, що аналізуються, визначають шляхом виміру інших властивостей зразків, які залежать від властивостей, що аналізуються, які, однак, на відміну від властивостей, що аналізуються, можуть легко вимірятися прямо протягом короткого проміжку часу й без руйнування зразка. Властивості зразків, які часто вимірюються, називають «первинними властивостями», а властивості зразків, що аналізуються, від яких залежать результати вимірів, але які не вимірюються безпосередньо, називають «вторинними властивостями». Одним з найбільш ефективних непрямих методів дослідження є спектроскопічний аналіз, при якому «вторинні» властивості зразків (наприклад, хімічний склад) визначаються за результатами вимірів їхніх спектральних характеристик, таких як оптичні спектри поглинання, відбиття або розсіювання, що виступають у якості «первинних» властивостей. 5 Для будь-якого непрямого методу аналізу властивостей зразків дуже важливим є етап визначення математичних співвідношень між результатами вимірів первинних властивостей зразка й значеннями величин, які характеризують вторинні властивості, що аналізуються. Ці співвідношення між вимірюваними на приладі первинними характеристиками й вторинними властивостями зразка, що аналізуються, називаються градуювальними моделями або просто градировками. Створення градуювальних моделей є однією з головних задач при використанні непрямих методів дослідження. Цей процес досить довгий і трудомісткий, особливо для випадку так званого багатомірного аналізу, коли для визначення кількісних характеристик вторинних властивостей зразка використовується набір результатів виміру великої кількості параметрів, які характеризують первинні властивості. Наприклад, у випадку спектроскопічного аналізу для визначення концентрації різних компонентів проводять виміри великої кількості . спектральних даних (величини поглинання, відбиття або розсіювання) для різних значень хвильових чисел (довжин хвиль, частот). Для побудови градуювальної моделі, яка дає задану точність визначення параметрів, що характеризують вторинні властивості довільного зразка, що аналізуються, необхідно провести аналіз великого набору зразків, схожих на зразки, які будуть аналізуватися на приладі надалі (градуювальний набір). Підбір зразків градуювального набору строго регламентується стандартами на різні непрямі методи аналізу, наприклад, стандартом на якісний аналіз за допомогою БІК спектроскопії [1]. Зразки градуювального набору повинні мати відомі значення параметрів, що характеризують аналізовані вторинні властивості, які визначаються за допомогою прямого референтного методу, який має задану точність і відтворюваність. У розглянутому раніше прикладі по спектроскопічному аналізу хімічного складу зразків, властивості зразків градуювального набору, що аналізуються, можуть бути попередньо визначені стандартними хімічними методами з використанням хімічних реакцій. Діапазон зміни вторинних властивостей зразків градуювального набору повинен повністю покривати діапазон можливих змін цих властивостей при аналізі невідомих зразків. Крім того, для створення найбільш стійкої моделі, зразки в градуювальному наборі повинні бути однорідно розподілені в діапазоні зміни властивостей, що аналізуються. Остаточні висновки щодо правильності підбору зразків градуювального набору й стійкості побудованої згідно з ним градуювальної моделі, можуть бути зроблені тільки після стандартної процедури валідації градуювальної моделі [1], оцінки числа ступенів свободи й визначення зразків, що випадають із градировки. Питання щодо стійкості градуювальної моделі є дуже важливим, тому що визначає область застосовності побудованої градировки. У випадку нестійкої градуювальної моделі, невеликі шумові зміни у вимірюваних первинних властивостях можуть привести до статистично значимих змін у результатах аналізу вторинних властивостей. Підвищення стійкості граду 86820 6 ювальної моделі здійснюється шляхом виключення із градуювального набору зразків з викидами в характеристиках. Пошук таких зразків здійснюється на підставі статистичного аналізу викидів, наприклад за відстанню Махаланобіса [1], що використовує дані вимірів первинних властивостей повного градуювального набору. Інше важливе питання, що виникає при використанні градуювальної моделі для визначення вторинних властивостей невідомого зразка - це оцінка того, наскільки точно побудована модель описує даний зразок і забезпечує необхідну точність визначення його вторинних властивостей. Виміряні первинні властивості зразка також піддають аналізу за статистикою визначення викидів. Критерієм застосовності градуювальної моделі для аналізу властивостей невідомого зразка може бути обчислена для даного зразка відстань Махаланобіса. Проблема застосовності градуювальної моделі для опису невідомого зразка перегукується із задачами, що розв'язуються при якісному аналізі, де на підставі виміру первинних властивостей зразка (спектральних даних) і зіставлення їх з бібліотечними даними, робиться висновок про набір компонентів у зразку. Відзначимо, що для визначення відстані Махаланобіса необхідно мати повну інформацію про результати вимірів первинних характеристик всіх зразків градуювального набору, причому умови вимірів зразка, що аналізується, й градуювальних зразків повинні бути ідентичними. На результати виміру первинних властивостей зразків, а як наслідок, і на точність визначення параметрів, які характеризують вторинні властивості зразків, що аналізуються, можуть істотно впливати зміни зовнішніх умов, а також технічні характеристики вимірювального приладу. Тому було запропоновано кілька способів створення градуювальних моделей, малосприйнятливих до зміни умов вимірів, а також кілька способів переносу градуювальних моделей між вимірювальними приладами, що дозволяє врахувати розходження в технічних характеристиках приладів і не повторювати складний процес побудови градуювальної моделі на кожному окремому приладі. Відомий спосіб створення багатомірних градуювальних моделей [2, 3], що мають малу сприйнятливість до зміни параметрів приладу, на якому проходять виміри, а також до зміни зовнішніх умов, при яких відбуваються виміри, і до зміни інших властивостей зразка. У даному способі для створення градуювальної моделі проводять виміри великої кількості параметрів, які характеризують первинні властивості зразка, для кожного зразка, з так званого градуювального набору зразків, з відомими вторинними властивостями. Зразки градуювального набору вибираються таким чином, щоб інші властивості зразків змінювалися в максимально можливому діапазоні. Крім того, при вимірі первинних властивостей зразків із градуювального набору навмисно роблять зміни параметрів вимірювального приладу, на якому проводять побудову градуювальної моделі, наприклад, у випадку спектрометрів вводять спектральні перекручування й зміну амплітуди вимірюваного сигналу. 7 Величина зміни параметрів приладу при побудові градуювальної моделі визначається максимально можливими величинами зміни цих параметрів, які очікуються між різними приладами при виробництві або будуть виникати в процесі експлуатації. Додатково вводять зміну зовнішніх умов. Зміни параметрів приладу або інших умов вимірів можуть також вводитися не в процесі проведення реальних вимірів, а шляхом математичних перетворень. Даний спосіб дозволяє створити багатомірну градуювальну модель, що дає результати аналізу вторинних властивостей зразка, які мало залежать від умов вимірів і приладу, на якому ці виміри проводилися, тому градуювальна модель створюється один раз і використовується без змін на всіх однотипних приладах. Навмисне введення розкиду даних результатів виміру зразків градуювального набору безумовно робить модель більше стійкою, а область застосовності побудованої даним способом градировки більше широкою. Однак точність результатів аналізу з використанням градуювальної моделі, яка створена за даним способом, буде знижена, тому що в моделі спочатку передбачається варіація результатів виміру первинних властивостей. Крім того, число факторів, які впливають на результати вимірів, дуже велике й не завжди можлива побудова математичної моделі, яка враховує вплив всіх можливих факторів. Тому для побудови повноцінної градуювальної моделі, яка враховує вплив великої кількості додаткових факторів, необхідно провести величезну кількість вимірів зразків градуювального набору при різних умовах, що робить і без того складний процес створення градуювальної моделі ще більш трудомістким і довгим. Останнім недоліком градуювальної моделі, створеної за допомогою даного методу, є те, що введення варіацій у результати вимірів зразків градуювального набору ускладнює оцінку правомірності застосування градуювальної моделі для аналізу того або іншого невідомого зразка, що може привести до помилок в аналізі вторинних властивостей. Наприклад, може виявитися так, що градуювальна модель для визначення процентного вмісту різних хімічних компонентів у зразку буде використана для аналізу невідомого зразка, який складається з інших компонентів, які у значній мірі відрізняються від зразків градуювального набору. Існує інший підхід до створення багатомірних градуювальних моделей, при якому не намагаються побудувати універсальну градуювальну модель, яка працює на всіх приладах і враховує всі можливі фактори, що впливають на результати вимірів. Замість цього, для того щоб градуювальна модель, побудована на одному приладі, який працює при одних умовах, дозволяла визначати вторинні властивості зразків за результатами вимірів первинних властивостей на іншому вимірювальному приладі, який відрізняється за технічними параметрами і працює в інших умовах, використовують спеціально розроблені способи переносу градировок. J. Shenk та ін. [4] запропонували спосіб переносу багатомірної градуювальної моделі між спек 86820 8 трометрами, заснований на перетворенні спектральних даних, виміряних на градуйованому приладі до виду, еквівалентному вимірам на опорному приладі, який використовувався для створення градуювальної моделі. Визначення вторинних властивостей невідомих зразків проводять після перетворення спектральних даних, прямо використовуючи створену на опорному приладі градуювальну модель. Спочатку градуювальна модель створюється на опорному спектрометрі з використанням методів багатомірного регресійного аналізу (таких як, багатолінійна регресія MLR, регресія основних компонентів PCR, або метод дробових найменших квадратів PLS), за допомогою яких знаходять співвідношення, що зв'язують відомі значення параметрів, які описують вторинні властивості зразків, що аналізуються, із градуювального набору з виміряними на опорному приладі спектральними характеристиками цих зразків (наприклад, зі спектрами поглинання). Для переносу градуювальної моделі на градуйований прилад використовується набір зразків для переносу градировок, також з відомими властивостями, що аналізуються; наприклад, це може бути частина зразків із градуювального набору. Спектральні характеристики зразків з набору для переносу градировок вимірюються, як на опорному, так і на й градуйованому приладах. Після чого, шляхом зіставлення результатів вимірів спектральних характеристик тих самих зразків на опорному й градуйованому спектрометрах, знаходять математичні співвідношення, які дозволяють перетворити спектральні дані, виміряні на градуйованому приладі на вид, еквівалентний результатам вимірів на опорному приладі. Знайдені математичні співвідношення щоразу використовують для виконання перетворень над результатами вимірів спектральних характеристик невідомого зразка на градуйованому приладі. Після чого градуювальна модель, створена на опорному спектрометрі, може бути застосована для визначення вторинних властивостей невідомого зразка. Більш детально процедура пошуку математичних співвідношень для перетворення спектральних даних виглядає в такий спосіб. На першому кроці визначають зсув хвильових чисел. Для визначення зсуву хвильових чисел обчислюються кореляційні коефіцієнти між спектральними даними, виміряними на опорному приладі при заданому хвильовому числі та спектральними даними, обмірюваними на градуйованому приладі при декількох найближчих до заданого значеннях хвильових чисел. Далі робиться припущення, що кореляційні коефіцієнти зв'язані квадратичною залежністю зі значеннями хвильових чисел у спектральних даних, виміряних на градуйованому приладі. Коефіцієнти даної квадратичної залежності визначаються методом найменших квадратів. Значення хвильового числа градуйованого приладу, при якому досягається максимум квадратичної залежності, відповідає заданому значенню хвильового числа опорного приладу, звідки визначаємо спектральний зсув для кожної точки в спектральних даних опорного приладу. Така процедура знаходження спектрального зсуву добре працює 9 для приладів зі скануючими дифракційними решітками в силу їх конструктивних особливостей. Після визначення спектрального зсуву проводять процедуру лінійної інтерполяції спектральних даних, виміряних на градуйованому приладі, де знаходять значення амплітуди вимірюваного сигналу при заданих значеннях хвильових чисел, які відповідають значенням хвильових чисел в опорних спектральних даних. Далі проводять амплітудне корегування інтерпольованих спектральних даних, знаходячи методом найменших квадратів коефіцієнти лінійного зв'язку між інтерпольованими спектральними даними й опорними спектральними даними. При деяких значеннях хвильових чисел неможливо знайти коригувальні коефіцієнти, оскільки значення спектральних даних у цих точках дорівнює нулю. Це може бути результатом математичної дообробки вихідних результатів вимірів, наприклад, диференціювання спектральних даних; у цьому випадку коригувальні амплітудні коефіцієнти для цих хвильових чисел знаходяться шляхом інтерполяції. Таким чином, результатом даного способу переносу градировок є: створена на опорному приладі градуювальна модель і дані необхідні для виконання перетворення результатів вимірів спектральних характеристик на градуйованому приладі у вид еквівалентний вимірам на опорному приладі, які включають величину спектрального зсуву й корегуючи амплітудні коефіцієнти для кожного значення хвильового числа. Недоліками даного методу є: вузька орієнтованість на спектрометри зі скануючими дифракційними решітками і великий обсяг обчислень, проведений на градуйованому приладі при аналізі невідомого зразка перед зіставленням обмірюваних спектральних характеристик із градуювальною моделлю для визначення цікавих вторинних властивостей. Це збільшує час обробки даних і вимагає високих обчислювальних потужностей, що може виявитися суттєвим при аналізі продукту безпосередньо в процесі виробництва, де швидкість одержання даних є ключовим параметром. Крім цього, у даному способі на градуйованому приладі не зберігаються дані щодо результатів вимірів градуювального набору, тому неможливо оцінити застосовність градуювальної моделі для аналізу невідомого зразка, що обмежує галузь застосування даного методу тими випадками, коли заздалегідь відомо, що невідомий зразок попадає в діапазон зміни спектральних даних, який покривається градуювальним набором. Відсутність даних про результати виміру зразків градуювального набору також не дозволяє розширити градуювальну модель шляхом виміру додаткових градуювальних зразків безпосередньо на градуйованому приладі, тому що для визначення зразків, які випадають із градуювального набору, необхідна повна інформація про результати вимірів всіх зразків градуювального набору. Розширення градировки без такої перевірки може привести до нестійкості градуювальної моделі. Найбільш повний опис методів переносу градуювальних моделей представлений в [5], де описані відразу кілька різних способів переносу гра 86820 10 дуювальних моделей. Хоча в даному патенті описуються способи переносу градировок між спектрометрами, дані методи можуть бути легко перенесені на будь-які інші прилади для аналізу однієї або декількох вторинних властивостей невідомого зразка за результатами виміру множини первинних властивостей цього зразка. У патенті розглянуті три основних способи переносу градуювальних моделей з опорного приладу на градуйований прилад. Як і в способі, запропонованому в [4], спочатку створюється градуювальна модель, заснована на спектральних даних, виміряних на опорному приладі для градуювального набору зразків з відомими властивостями, що аналізуються. Потім, із градуювального набору вибирається частина зразків і створюється набір для переносу градировок, який вимірюється на градуйованому приладі, і використовується для визначення співвідношень переносу градировок. Для достовірного визначення співвідношень переносу градировок зразки з набору для переносу градировок повинні забезпечувати достатню кількість інформації про особливості результатів вимірів спектральних даних на різних приладах. Тому кількість цих зразків повинна бути не менше рангу матриці коефіцієнтів градуювальної моделі, створеної на опорному приладі. Далі перенос градуювальної моделі здійснюється шляхом зіставлення спектральних даних, обмірених на опорному й градуйованому приладі відповідно до одного із запропонованих способів. У першому способі, названому авторами «класичним», передбачається, що для зразків з набору для переносу градировок відомі всі аналізовані вторинні властивості, наприклад, концентрації складових, зразки хімічних компонентів. Тоді зв'язок між обміреними спектральними даними й відомими властивостями зразків визначається двома різними градуювальними моделями для опорного й градуйованого приладу. Це може бути записане в матричній формі як. R1=CK1 (1) R2=CK2=C(K1+DK) де R1 - матриця спектральних даних, виміряних на опорному приладі, яка має розмірність m X n; R2 - аналогічна матриця спектральних даних, виміряних на градуйованому приладі; n - число спектральних точок у результатах вимірів, m - кількість зразків у наборі для переносу градировок, С - матриця властивостей зразків (концентрацій), які визначаються, що має розмірність m X с; с число властивостей, які визначаються; K1 - опорна калібрована модель, K2 - скоригована калібрована модель, представлена у вигляді матриць коефіцієнтів, що мають розмірність с X n. Матриця коефіцієнтів коригування має вигляд. (2) DK=C+(R2-R1) де С+ - псевдо або узагальнена зворотна матриця властивостей зразків (тому що матриця С у загальному випадку неквадратна). Використовуючи вираження (1) і (2) ми можемо знайти спектральні дані, які були б отримані шляхом виміру всього градуювального набору зразків на градуйованому приладі, після чого побудувати 11 нову градуювальну модель. Таким чином, «класичний» спосіб переносу градировок використовує відомі властивості зразків з набору для переносу градировок для того, щоб визначити коригувальні коефіцієнти. Ці коефіцієнти визначають зв'язок між вторинними властивостями зразків з набору для переносу градировок і вимірюваними на градуйованому приладі первинними властивостями цих зразків. Після чого, виходячи з відомих вторинних властивостей зразків повного градуювального набору, використовуючи дані коефіцієнти корегування, знаходять первинні властивості для кожного зразка з повного градуювального набору, емулюючі вимір градуювального набору на градуйованому приладі. Використовуючи обчислені значення первинних властивостей зразків градуювального набору й відомі вторинні властивості цих зразків, за допомогою методів регресійного аналізу створюють нову градуювальну модель для градуйованого приладу, що використовується надалі для визначення вторинних властивостей невідомого зразка за результатами виміру первинних властивостей цього зразка на градуйованому приладі. Класичний спосіб переносу градировок можливо використати тільки в тому випадку, коли точно відомі всі властивості зразків із градуювального набору, наприклад, є точні дані про концентрації всіх хімічних елементів, що складають зразок. Крім того, набір зразків для переносу градировок - це частина зразків з повного градуювального набору, для яких також повинні бути відомі всі вторинні властивості. Крім того, даний метод негласно припускає, що скоригована за набором для переносу градуювальна модель має достатню точність передбачення й стійка, хоча реальної валідації не здійснюється. Як показує досвід [5], для даного методу характерна відносно невисока вірогідність визначення властивостей зразка. У випадку, коли немає необхідності у визначенні всіх вторинних властивостей зразків, а цікавить лише одна певна властивість, наприклад, вміст білка, в [5] запропоновано використати «зворотний» спосіб переносу градировок. Модифікований «зворотний» спосіб був також запропонований в [6]. У цьому способі обсяг математичних обчислень значно зменшується в порівнянні з «класичним» способом, тому що матриця концентрацій вироджується у вектор «с» розмірності m, і градуювальна модель також описується вектором коефіцієнтів «b» розмірності n. Спочатку, стандартним способом, використовуючи багатомірний регресійний аналіз, за градуювальним набором зразків створюється градуювальна модель на опорному приладі, яка визначає співвідношення, що зв'язують матрицю спектральних даних або інших первинних властивостей зразків з набору для переносу градировок, обмірюваних на опорному приладі (R1) і вторинну властивість цих зразків, яка визначається. c=R1b1 (3) Далі проводять вимір тих самих зразків з набору для переносу градировок на градуйованому приладі, причому коефіцієнти градуювальної моделі коригуються для одержання відомих значень 86820 12 характеристик, які описують вторинні властивості зразків з набору для переносу градировок. с=R2b2=R2(b1+Db) (4) У підсумку, вектор коефіцієнтів нової градуювальної моделі можна виразити через вектор коефіцієнтів опорної градуювальної моделі й зворотні матриці результатів виміру первинних властивостей (спектральних даних) зразків з набору для переносу градировок на опорному й градуйованому приладах відповідно. b2=b1+(R+2-R+1)c (5) На відміну від «класичного» способу переносу градировок в «зворотному» способі не проводиться корекція всіх результатів виміру первинних властивостей зразків градуювального набору на опорному приладі з метою приведення їх до виду, еквівалентному результатам виміру на градуйованому приладі. У цьому методі на підставі вимірів зразків набору для перенесення градировок знаходяться скориговані коефіцієнти градуювальної моделі, які згодом використовуються для визначення вторинних властивостей невідомого зразка. Даний метод може бути розширений для випадку, коли одночасно досліджуються кілька властивостей зразка. Тоді вектори будуть замінені на матриці. Основна перевага даного методу переносу градировок у тім, що для його реалізації необхідні відносно невисокі обчислювальні потужності. Причому, результатом застосування даного методу переносу градировок є скориговані коефіцієнти градуювальної моделі, побудованої на опорному приладі, які прямо використовуються для визначення вторинних властивостей за результатами виміру первинних властивостей на градуйованому приладі, що суттєво скорочує час аналізу невідомого зразка. Однак для досягнення високої точності визначення властивостей невідомих зразків на градуйованому приладі, необхідно використати велику кількість зразків у наборі для переносу градировок. Чим більше набір зразків, тим вище точність. Як і в «класичному» способі в «зворотному» способі немає можливості оцінити застосовність перенесеної градуювальної моделі для аналізу невідомого зразка, виміряного на градуйованому приладі, тому що для цього необхідно мати інформацію про спектральні дані для всіх зразків градуювального набору, виміряних в умовах, еквівалентних умовам виміру невідомого зразка. Третій спосіб переносу градировок, описаний в [5], автори назвали «прямим» способом. У цьому способі, використовуючи результати виміру первинних властивостей (спектральних характеристик) зразків з набору для переносу градировок, отриманих на опорному й градуйованому приладі, знаходять матрицю перетворення результатів виміру (F), яка визначає функціональний зв'язок між результатами виміру первинних властивостей довільного зразка на опорному приладі й результатами виміру цього ж зразка на градуйованому приладі. F=R+2R1 (6) Після чого, первинні властивості довільного зразка, виміряні на градуйованому приладі, мо 13 жуть бути доведені до виду еквівалентному результатам виміру цього зразка на опорному приладі. r1'=r2F (7) г2 - результати виміру первинних властивостей зразка на градуйованому приладі, а r1'- результат математичного перетворення результатів виміру первинних властивостей зразка на градуйованому приладі у вид еквівалентний результатам виміру на опорному приладі. У даному методі математичні співвідношення зв'язують кожне значення первинних властивостей зразка, перетворених у вид еквівалентний результатам виміру на опорному приладі з кожним значенням, виміряним на градуйованому приладі. Це означає, що кожна точка в спектральних даних перетворених у вид опорного приладу, є функцією спектральних даних у всіх точках, виміряних на градуйованому приладі. Це робить перенос градировок найбільш точним, однак це також є причиною одного з недоліків даного способу. А саме того, що перетворення спектральних даних з використанням «прямого» методу вимагає високих обчислювальних потужностей і може суттєво здорожувати прилад. Число зразків у наборі для переносу градировок повинне дорівнювати, як мінімум, рангу матриці спектральних даних для повного градуювального набору, виміряного на опорному приладі, а матриця перетворення результатів вимірів, яка використовується в даному способі, має розмірність n X n, де n - число спектральних точок, у яких роблять вимірювання, причому п, як правило, велике число і його значення може перевищувати 100. Крім того, щораз перед визначенням вторинних властивостей зразка, які аналізуються, необхідно провести математичні перетворення обмірюваних даних у вид опорного приладу, що може значно збільшити час аналізу. Відзначимо, що в описаному способі переносу градуювальних моделей за допомогою тих або інших перетворень, первинні властивості зразків, обмірювані на градуйованому приладі, приводяться до виду еквівалентному результатам виміру на опорному приладі, після чого для визначення вторинних властивостей, що аналізуються, використовується градуювальна модель, створена на опорному приладі. Причому градуювальна модель, створена на опорному приладі, повинна пройти стандартну процедуру валідації [1], що гарантує стійкість моделі, однак це не є достатньою умовою того, що дана модель стійка при аналізі результатів вимірів, отриманих на градуйованому приладі й перетворених у вид, еквівалентний результатам вимірів на опорному приладі. Для цього результати вимірів невідомого зразка потрібно проаналізувати на присутність даних, які випадають, за допомогою статистики передбачення викидів, наприклад, статистики Махаланобіса, для чого необхідна інформація про результати вимірів зразків повного градуювального набору, а не тільки дані про константи в математичних співвідношеннях градуювальної моделі. Тому в деяких випадках, корисно мати окрему "незалежну" градуювальну модель. Під терміном «незалежна модель» ми маємо на увазі таку градуювальну модель, яка 86820 14 створюється окремо для кожного приладу, що градуюється, ураховує його особливості, дає можливість оцінки застосовності для аналізу того або іншого невідомого зразка й гарантує стійкість. Незалежна градуювальна модель може бути розширена шляхом простого виміру додаткових градуювальних зразків на градуйованому приладі без використання опорного приладу, наприклад, для коректування градуювальної моделі при зміні параметрів приладу, який градуюється, в процесі експлуатації (старіння). Відомий спосіб переносу градуювальних моделей між приладами [7], також орієнтований на перенос градировок між спектрометрами. По сукупності суттєвих ознак даний спосіб є найбільш близьким до винаходу, що заявляється. Даний спосіб містить у собі: визначення спектральної передатної функції опорного спектрометра й спектрометра, що градуюється, шляхом виміру спектральних даних на обох приладах для монохроматичного джерела світла; визначення кореляційних співвідношень між спектральними передаточними функціями опорного спектрометра й спектрометра, що градуюється, і знаходження математичних співвідношень перетворення результатів вимірів на опорному приладі у вид, еквівалентний результатам вимірів на градуйованому приладі; підбор зразків градуювального набору з відомими властивостями, що аналізуються; виміру на опорному спектрометрі спектральних характеристик кожного зразка із градуювального набору; перетворення за допомогою знайдених співвідношень спектроскопічних даних для зразків градуювального набору, виміряних на опорному спектрометрі, у вид еквівалентний результатам вимірів зразків градуювального набору на градуйованому спектрометрі; і створення градуювальної моделі для градуйованого спектрометра, шляхом визначення за допомогою методів регресійного аналізу співвідношень між відомими властивостями зразків градуювального набору й перетвореними спектральними даними. Градуювальна модель, створена на градуйованому приладі за допомогою даного способу, є повністю незалежною від опорного приладу. Причому даний спосіб дає можливість не повторювати виміру зразків градуювального набору на кожному градуйованому приладі, а використовує перетворені у вид приладу, що градуюється, дані, обмірювані на опорному приладі. Така градуювальна модель може бути легко доповнена й розширена шляхом виміру додаткових градуювальних зразків, безпосередньо на градуйованому приладі. Однак співвідношення для перетворення результатів вимірів, проведених на опорному приладі, у вид, еквівалентний вимірам на градуйованому приладі, встановлюються шляхом порівняння відгуків обох приладів на теж саме джерело монохроматичного світла. Тому даний метод придатний лише для спектрометрів, і не може бути використаний для приладів, що використовують інші принципи аналізу, коли вимірюються інші не спектроскопічні первинні властивості зразків. Відзначимо, що для одержання достовірного переносу градировок монохроматичне джерело повинно мати 15 безпрецедентно високу стабільність. Таке джерело випромінювання, як правило, має високу вартість і не завжди може бути доступним. Головним недоліком даного методу є те, що використання тільки однієї монохроматичної лінії випромінювання не дозволяє знайти точних співвідношень для перетворення спектральних даних. Теорія спектральної передаточної функції розроблена для лінійного наближення. Однак, дуже часто варіації в характеристиках приладів мають нелінійний характер, наприклад, зсув довжини хвилі в приладах зі скануючими дифракційними решітками [4]. Таким чином, використання математичних перетворень, отриманих даним способом, може привести до невірних результатів переносу спектральних даних у випадку нелінійних змін у характеристиках приладів. Крім того, даний метод переносу градировок не враховує варіації в інтенсивності й спектрі випромінювання поліхроматичних джерел світла в самих градуйованих спектрометрах. Задачею даного винаходу є створення незалежної градуювальної моделі для визначення одного або декількох вторинних властивостей невідомого зразка за результатами вимірів численних первинних властивостей цього зразка, не обов'язково спектральних, яка забезпечує високу точність визначення властивостей, що аналізуються, і враховує нелінійні відмінності технічних параметрів градуйованого й опорного приладів і вплив умов експлуатації, а крім того, дає можливість розширення й доповнення, шляхом виміру додаткових градуювальних зразків на градуйованому приладі. Поставлена задача вирішується способом створення незалежних багатомірних градуювальник моделей, який включає послідовність дій, об'єднаних єдиним винахідницьким задумом. Спосіб включає підбір градуювального набору зразків з відомими вторинними властивостями, що визначені референтними методами; вимір на опорному приладі первинних властивостей кожного зі зразків градуювального набору з відомими вторинними властивостями й перетворення результатів виміру первинних властивостей зразків градуювального набору за допомогою співвідношень переносу градировок у вид, як якби виміри проводилися на градуйованому приладі; створення градуювальної моделі шляхом знаходження за допомогою методів регресійного аналізу з використанням перетворених даних співвідношень градировки, які дозволяють визначити вторинні властивості невідомого зразка, що аналізуються, за результатами вимірів множини первинних властивостей цього зразка, проведених на градуйованому приладі, та відрізняється тим, що співвідношення переносу градировок знаходять, підбираючи набір зразків для переносу градировок, вимірюючи первинні властивості кожного зразка з набору для переносу градировок на опорному й градуйованому приладах і зіставляючи за допомогою методів багатомірного регресійного аналізу результати вимірів первинних властивостей зразків набору для переносу градировок, отримані на опорному приладі, з результатами виміру первинних властивостей тих же самих зразків, отриманими на градуйованому приладі, а 86820 16 знайдені співвідношення градировки вибирають у якості оптимальної градуювальної моделі використовуючи процедуру перевірки точності (валідації). Використання набору зразків для переносу градировок дозволяє врахувати нелінійні зміни в характеристиках приладів, тому що для знаходження співвідношень перетворення результатів вимірів використовується кілька залежностей зміни первинних властивостей. Крім того, всі результати вимірів зразків градуювального набору перетворюються у вид, еквівалентний результатам вимірів на градуйованому приладі, і зберігаються в комп'ютері градуйованого приладу. Це робить модель, створену за допомогою даного способу, повністю незалежною від вимірів на опорному приладі, і дозволяє при вимірюванні невідомого зразка на градуйованому приладі проводити аналіз даних, що випадають, за допомогою статистики передбачення викидів, що гарантує високу точність визначення вторинних властивостей, що аналізуються. Запропоновані різні способи підбору зразків у набір для переносу градировок. Проведення на заключному етапі процедури перевірки точності (валідації) гарантує, що побудована модель задовольняє заданій точності аналізу вторинних властивостей невідомих зразків. Валідація градировки здійснюється шляхом порівняння вторинних властивостей зразків, визначаючи їх з результатів вимірів на градуйованому приладі за допомогою співвідношень градировки з прямими результатами виміру вторинних властивостей за допомогою референтних методів. Передбачена можливість розширення створеної градуювальної моделі з метою підвищення точності аналізу й стійкості моделі шляхом доповнення результатів вимірів первинних властивостей зразків градуювального набору, перетворених у вид, як якби виміри проводилися на градуйованому приладі, результатами вимірів первинних властивостей додаткових градуювальних зразків з відомими вторинними властивостями, проведеними на градуйованому приладі й находження математичних співвідношень градировки по доповненим градировочним даним, причому створювана градуювальна модель є повністю незалежною від аналогічної градуювальної моделі, побудованої на опорному або будь-якому іншому приладі. Передбачена можливість переносу доповнених градуювальних даних на інший прилад, у тому числі назад на опорний, після чого створюють нову градуювальну модель, причому прилад, на якому проводилися виміру додаткових градуювальних зразків, виступає в якості нового опорного приладу. З метою підвищення стійкості градуювальної моделі, що створюється, запропоновано використовувати статистику передбачення викидів, і виключати з моделі зразки градуювального набору, що випадають, перед визначенням співвідношень градировки. Запропоновано використати процедуру нормалізації результатів вимірів і референтних даних, що забезпечує мінімальну погрішність визначення аналізованих вторинних властивостей і що дозво 17 ляє враховувати технічні особливості приладу, на якому проводяться вимірювання, а також розходження пробопідготовки й стану досліджуваного зразка. Процедура нормалізації являє собою вибір того або іншого методу математичної передобробки. Критерієм вибору передобробки є точність аналізу вторинних властивостей зразків, яку забезпечує градуйований прилад із градировкою, при створенні якої використовувався даний вид математичної передобробки. У якості основних кількісних критеріїв використовуються кількісні параметри процедури валідації градуювальної моделі (наприклад, стандартна помилка кросвалідації) [1]. Також розглянуті особливості реалізації пропонованого способу на спектрометрах, які використовують принципи Фур'є-спектроскопії. Суть винаходу полягає у тому, що запропонована сукупність ознак дозволяє створити на градуйованому вимірювальному приладі повністю незалежну градуювальну модель, яка дає можливість із високою точністю передбачати вторинні властивості невідомих зразків за результатами виміру багатьох первинних, не обов'язково спектроскопічних, властивостей, яка враховує нелінійні розходження в технічних параметрах градуйованого й опорного приладів, а також особливості умов експлуатації, причому градуювальна модель будується на основі даних стосовно первинних властивостей зразків із градуювального набору, виміряних на опорному приладі й перетворених у вид, як якби виміри проводилися на градуйованому приладі. Вид перетворення результатів вимірів зразків градуювального набору у вид, еквівалентний результатам вимірів на градуйованому приладі, визначається з вимірів набору зразків для переносу градировок на обох приладах, причому набір для переносу градировок складається з набагато меншої кількості зразків, чим градуювальний набір. Зразки з набору для переносу градировок забезпечують суттєві розходження в результатах вимірів у всьому діапазоні первинних властивостей як на опорному, так і на градуйованому приладах. Використання набору зразків для переносу градировок дозволяє визначити нелінійний зв'язок між результатами вимірів тих самих зразків на різних приладах шляхом кореляційного аналізу з використанням регресійних методів. Крім того, оскільки створювана градуювальна модель повністю незалежна й при її побудові використовуються результати вимірів первинних властивостей зразків градуювального набору, доведені до виду градуйованого приладу, оцінка застосовності побудованої градуювальної моделі для аналізу невідомого зразка може бути проведена стандартними методами з використанням статистичних методів визначення викидів даних, наприклад, шляхом визначення відстані Махаланобіса. З метою підвищення точності аналізу градуювальна модель може бути доповнена шляхом виміру додаткових градуювальних зразків на градуйованому приладі. Крім того, запропоновано використати процедуру нормалізації з використанням різних видів математичної передобробки результатів вимірів і даних стосовно вторинних властивостей (референтних 86820 18 даних), що дозволяють урахувати впливи факторів, що заважають, таких як розходження у пробопідготовці й у стані зразків. Суть винаходу, що заявляється, пояснюється малюнком, де на Фіг. наведене схематичне зображення способу, який заявляється, у вигляді потокової діаграми. Спосіб створення незалежних градуювальних моделей, який заявляється, може бути використаний для будь-яких вимірювальних приладів, де за результатами багаторазового виміру первинних властивостей, визначають значення параметрів, які характеризують деякі вторинні властивості, зокрема для різного виду спектрометрів, наприклад, для БІК і ІК спектроаналізаторів, які вимірюють поглинання світлового випромінювання зразком при різних значеннях довжини хвилі випромінювання. Результати таких вимірів прийнято називати спектральними даними або просто спектрами. Розглянемо застосування способу, який заявляється, на прикладі спектрометрів для аналізу хімічного складу зразка. Однак варто ще раз підкреслити, що галузь застосування способу, який заявляється, не обмежується спектроскопією, і в наведеному нижче описі спектрометри використовуються лише як найбільш наочний приклад. Як уже говорилося, градуювальна модель визначає зв'язок між результатами вимірів, спектром, у випадку спектрометра, і властивостями зразка, що аналізуються. Відзначимо, що часто з властивостями зразка, що аналізуються, порівнюються не безпосередньо результати вимірів, а спектральні дані, що вже пройшли процедуру нормалізації (попередню математичну передобробку). Так, наприклад, може проводитися згладжування спектрів, віднімання базової лінії або диференціювання. Вид попередньої математичної обробки при виконанні процедури нормалізації вибирається виходячи з критерію максимальної точності визначення вторинних властивостей, що аналізуються, тому математичні операції, які виконуються, повинні перетворювати спектральні дані таким чином, щоб у перетворених спектральних даних вплив досліджуваних властивостей виявлявся в найбільш явному виді й зводився до мінімуму вплив побічних факторів, пов'язаних з паразитним розсіюванням і особливостями пробопідготовки. Та ж сама математична передобробка застосовується до всіх спектрів зразків градуювального набору. Тобто, якщо до попередньої математичної обробки вид спектрів змінювався незначно при зміні досліджуваних властивостей зразків, то після проведення процедури нормалізації перетворені спектральні дані мають яскраво виражені зміни навіть при незначних змінах аналізованих властивостей. Як критерії для оцінки точності передбачення використовуються статистичні характеристики градуювальної моделі, такі як стандартна помилка калібрування (SEC), стандартна помилка валідації (SEV) і стандартна помилка крос-валідації (SECV) [1]. Найпоширенішим видом математичної передобробки при спектральному аналізі є знаходження середньозважених значень спектральних даних [8], що зменшує на 1 число ступенів свободи в градуювальній мо 19 86820 делі. У даній передобробці знаходять усереднений по всьому градуювальному наборі спектр і віднімають його від кожного індивідуального спектра градуювальних зразків. Аналогічним чином знаходять середньозважені значення референтних даних. Тоді при аналізі невідомого зразка перед застосуванням побудованої градуювальної моделі від виміряного спектра також віднімається усереднений за градуювальним набором спектр. Для того щоб створити градуювальну модель для спектрометра, спочатку проводять виміри спектральних даних для великого набору зразків (градуювального набору). Зразки градуювального набору для спектрального аналізу вибираються за наступними критеріями [1]: а) зразки повинні містити всі хімічні компоненти, які планується аналізувати; б) діапазон зміни концентрації компонентів, що аналізуються, у зразках градуювального набору повинен перевищувати діапазон зміни в невідомих зразках, що аналізуються; в) величини зміни в концентрації хімічних компонентів від зразка до зразка повинні бути рівномірно розподілені по всьому діапазоні змін; г) число зразків повинне забезпечуватизнаходження за допомогою статистичних методів математичних співвідношень між спектроскопічними даними й концентрацією окремих хімічних компонентів. Визначення зразків, що випадають із градуювального набору, здійснюється за допомогою статистичного аналізу викидів, наприклад, шляхом обчислення відстані Махаланобіса [1], що визначається як: D2=rt(R·Rt)+r (8) де R - матриця спектральних даних повного градуювального набору, r - вектор, що відповідає спектру одного зразка. Відстань Махаланобіса показує скільки ступенів свободи вносить у градуювальну модель даний зразок. У середньому кожний градювальний зразок повинен вносити k/m, де k - число перемінних у регресії, m - число зразків у градуювальному наборі. Зразки з D2>3k/m повинні бути виключені із градуювального набору. Велике значення відстані Махалонобіса означає, що спектр даного зразка майже повністю визначає один з регресійних коефіцієнтів, що робить модель нестійкою. Таке може відбутися, коли наприклад порушена однорідність і рівномірність розподілу властивостей градуювальних зразків, що аналізуються, по діапазоні, у якому вони змінюються, тобто коли склад зразка суттєво відрізняється від інших зразків у градуювальному наборі. Із градуювального набору повинні бути також виключені зразки, значення аналізованих властивостей, що аналізуються, яких, визначені за допомогою побудованої моделі, значно відрізняються від значень, які дає референтний метод. Дані зразки визначаються з розбіжностей по Стьюденту, розрахованих за формулою: t = (9) тут eі - відмінність отриманої за допомогою градуювальної моделі величини концентрації хімічного компонента або властивості, що аналізується, й референтного значення для і-го градуювального зразка, SEC - стандартна помилка 20 калібрування [1], D2i - відстань Махаланобіса для іго градуювального зразка. Розбіжності за Стьюдентом повинні бути рівномірно розподілені за нормальним законом. Величина розбіжності порівнюється з коефіцієнтом Стьюдента, для довірчої ймовірності 0,95 і числа ступенів свободи m-k. У випадку якщо величина розбіжності перевищує коефіцієнт, зразок виключається із градуювального набору. Досліджувані властивості зразків градуювального набору заздалегідь відомі або виміряються референтним способом, наприклад, за допомогою традиційних хімічних методів з використанням реактивів. Оскільки оптичні виміри при спектральному аналізі проводяться при заданому об'ємі зразка, який визначається довжиною оптичного шляху, бажано щоб референтні дані були виражені в об'ємних одиницях. Високі вимоги пред'являються до точності й відтворюваності референтного методу, тому що від цього прямо залежить точність і спектрального аналізу. Точність референтного методу може бути підвищена шляхом багаторазового виміру и усереднення референтних даних. Після виміру спектральних характеристик зразків градуювального набору на опорному приладі може бути створена багатомірна градуювальна модель. Для цього використовуються відомі математичні методи регресійного аналізу, такі як, багатомірна лінійна регресія (MLR), аналіз принципових компонентів (РСА), метод дробових найменших квадратів (PLS) або метод нейронних сіток (ANN). Тоді, вимірюючи спектр невідомого зразка на опорному приладі й використовуючи створену градуювальну модель, ми можемо визначити властивості, що аналізуються, наприклад, концентрацію одного або декількох хімічних елементів, процентний склад протеїну, жиру або крохмалю й т.п. Створена градуювальна модель дозволяє з високою точністю передбачати властивості зразків, вимірюючи їхні спектри на спектрометрі, на якому проводилися виміру всіх зразків градуювального набору. При використанні іншого, навіть однотипного спектрометра, точність прередбачень із використанням градуювальної моделі, створеної на іншому приладі, значно знижується, що пов'язане з варіацією технічних характеристик спектрометрів і різних умов експлуатації. Крім того, може виявитися, що зміни в спектральних даних того самого зразка, виміряного на різних приладах, виходять за межі області застосування побудованої градуювальної моделі, яка визначається максимально припустимим значенням відстані Махаланобіса. Тоді створена на опорному приладі градуювальна модель взагалі не може бути застосована для аналізу. Таким чином, для точного передбачення властивостей невідомих зразків на кожному приладі необхідно мати свою незалежну градуювальну модель, яка враховує нелінійні розходження в характеристиках приладів і дає задану точність аналізу, а також дозволяє оцінити застосовність моделі для аналізу невідомого зразка за допомогою статистичних методів визначення викидів, наприклад шляхом визначення відстані Махаланобіса. Крім того, у процесі експлуатації тех 21 нічні характеристики приладів можуть змінюватися, що також може привести до зниження точності передбачень і необхідності побудови нової градуювальної моделі. Спосіб, що заявляється, дозволяє створювати повністю незалежні градуювальні моделі для різних приладів і проводити коригування вже створеної градуювальної моделі без виміру повного набору градуювальних зразків на градуйованому приладі. Для створення нової градуювальної моделі використовуються спектральні дані, виміряні на опорному приладі, однак перетворені у вид еквівалентний вимірам на градуйованому спектрометрі. Область застосування й стійкість нової градуювальної моделі аналізуються на підставі перетворених спектральних даних. Оскільки всі дані за результатами вимірів зразків градуювального набору перетворюються у вид еквівалентний результатам вимірів на градуйованому приладі, при аналізі невідомого зразка на градуйованому приладі вони можуть бути використані для оцінки викидів даних, наприклад шляхом визначення відстані Махаланобіаса для обмірюваного на градуйованому приладі спектра невідомого зразка. Для визначення співвідношень перетворення спектральних даних зразків градуювального набору у вид еквівалентний результатам вимірів на градуйованому приладі, використовується набір зразків, не обов'язково з відомими властивостями, які аналізуються, що забезпечують максимально можливі варіації вимірюваних спектральних даних, називаний надалі як набір для переносу градировок. Спектр кожного зразка з набору для переносу градировок вимірюється на обох, опорному (де проводилось виміру спектрів зразків градуювального набору) і градуйованому (для якого створюється нова градуювальна модель) приладах. Проводячи кореляцію спектральних даних для зразків з набору для переносу градировок, виміряних на опорному й градуйованому приладі, знаходять співвідношення, що дозволяють перетворити спектри, виміряні на опорному приладі у вид, як якби виміри проводилися на градуйованому приладі і враховують нелінійні розбіжності в результатах вимірів тих самих зразків на різних приладах. Для кореляції можна використати як безпосередньо результати вимірів, так і спектральні дані, що пройшли процедуру нормалізації, яка полягає в попередній математичній обробці, при цьому однакові математичні перетворювання використовуються для всіх обмірюваних спектрів. Математичні перетворювання повинні забезпечувати виявлення явних відмінностей у спектральних даних, виміряних на різних приладах, що забезпечить більш точне визначення виразів для перетворення спектральних даних виміряних на опорному приладі до виду еквівалентному результатам вимірів на градуйованому приладі. Після того як знайдені вирази для перетворення спектральних даних, спектральні дані для кожного зразка із градуювального набору можуть бути перетворені у вид, що відповідає вимірам на градуйованому приладі. Далі, використовуючи стандартні математичні методи багатомірного регресійного аналізу (MLR, PCA, PLS і т.п.[8]) по пе 86820 22 ретвореним спектральним даним створюють градуювальну модель для градуйованого приладу. Після чого властивості невідомого зразка можуть бути визначені по вимірам спектральних даних на градуйованому приладі з використанням нової незалежної градуювальної моделі. У способі, що заявляється, більша частина обчислень по перетворенню спектральних даних виконується на стадії створення градуювальної моделі, а не аналізу зразка (не потрібно трудомісткого перетворення у вид еквівалентний результатам вимірів на опорному приладі), що дозволяє скоротити час аналізу. Також відзначимо, що спосіб, який заявляється, створює повністю незалежну градуювальну модель на кожному градуйованому приладі, хоча виміри градуювального набору зразків проводяться лише однократно. Перетворення спектральних даних для кожного зразка градуювального набору у вид еквівалентний результатам вимірів на градуйованому приладі дозволяють проводити пошук, зразків, які випадають із градировки для даного конкретного градуйованого приладу, що гарантує стійкість створеної моделі. При аналізі невідомих зразків незалежність градуювальної моделі дає можливість провести оцінку результатів вимірів на викиди в спектральних даних, наприклад за допомогою статистики Махаланобіса, що дозволяє оцінити застосовність створеної градуювальної моделі й очікувану точність аналізу зразка. Для переносу спектральних даних градуювального набору на градуйований прилад використовується спеціально підібраний набір зразків для переносу градировок, число зразків у якому набагато менше, ніж у повному градуювальному наборі, при цьому їхні властивості можуть бути невідомі, важливо лише те, що цей набір зразків забезпечує значні варіації у виміряних спектральних даних, які дозволяють знайти вирази перетворення. Незалежність градуювальної моделі дає можливість доповнення й розширення градировки шляхом виміру додаткових градуювальних зразків з відомими (або обмірюваними референтними методами) властивостями, що аналізуються, безпосередньо на градуйованому приладі До матриці перетворених у вид градуйованого приладу спектральних даних для повного градуювального набору додаються спектри додаткових зразків, які можуть бути перевірені по статистиці Махаланобіса на наявність викидів, чим забезпечується стійкість розширеної градуювальної моделі. Таке розширення дозволяє підвищити точність результатів аналізу властивостей невідомих зразків з більш глибоким урахуванням характерних рис градуйованого приладу, умов експлуатації й особливостей аналізованих зразків (пробопідготовка, чистота й т.п.). Наприклад, якщо прилад проводить виміри продукту на деякій стадії його виробництва, всі попередні стадії виробництва можуть впливати не тільки на властивості зразка, що аналізуються, але й на інші властивості продукту, які відбиваються в змінах вимірюваних спектральних даних, що може привести до неточного передбачення властивос 23 тей, що аналізуються; щоб підвищити точність передбачень можна доповнити градуювальну модель вимірами декількох додаткових градуювальних зразків, які пройшли всі попередні стадії обробки, властивості яких точно визначаються референтним методом. Іншим прикладом може служити доповнення градуювальної моделі зразками сільськогосподарської продукції, яка вирощена в конкретному регіоні або зібрана в певний урожай. Незалежність створеної за допомогою способу, що заявляється, градуювальної моделі дозволяє переносити вже доповнену на градуйованому приладі модель на будь-який інший прилад, використовуючи той же спосіб, що й при переносі з опорного приладу на градуйований прилад. Це дуже зручно, тому що дозволяє накопичувати градуювальні дані, так, наприклад, при розширенні виробництва й запусканні нової лінії, можна використати доповнену градировку, яка враховує особливості виробничого циклу й властивості використовуваної сировини, та отримана на приладі, що працює на вже діючій лінії. Оскільки для створення кожної нової незалежної градуювальної моделі використовується повний набір спектрів для всіх зразків градуювального набору, перетворений у вид градуйованого приладу, даний спосіб дозволяє проводити оцінку даних, що випадають, наприклад, по відстані Махаланобіса, для невідомого зразка, що аналізується, прямо на градуйованому приладі й визначати зразки, що випадають. Інша перевага, що дає даний спосіб, а точніше незалежність градуювальної моделі, полягає в тому, що після того, як було здійснене перетворення спектральних даних для всіх зразків із градуювального набору, ці дані можна піддати процедурі нормалізації шляхом додаткової математичної обробки. Таким чином, ми одержуємо можливість використовувати на кожному градуйованому приладі при здійсненні процедури нормалізації свій незалежний метод попередньої математичної обробки, який враховує особливості кожного окремого приладу, що суттєво підвищує точність передбачень. Це особливо корисно, коли градуювальна модель переноситься з опорного приладу одного типу на градуйований прилад іншого типу, наприклад зі спектрометра на базі скануючих дифракційних решіток на спектрометр, який використовує принципи Фур'є-спектроскопії. Відзначимо, що спосіб, який заявляється, може бути використаний також для переградировки одного приладу, з огляду на зміни в характеристиках приладу, що виникають у процесі експлуатації (старіння). Для ілюстрації способу, що заявляється, наведемо приклад створення незалежних градуювальних моделей для визначення показників якості продовольчої пшениці на декількох спектрометрах ІнфраЛЮМ ФТ-10, розміщених на різних елеваторах Краснодарського краю. Даний вид спектрометрів використовує принципи Фур'є - спектроскопії в ближній інфрачервоній області спектра (БІК). Однак, ще раз підкреслимо, що наведений приклад використовується лише для ілюстрації й більше 86820 24 чіткого розуміння основних принципів пропонованого способу й не в якій мері не обмежує рамки даного винаходу. Спочатку на опорному спектрометрі проводяться виміри спектрів зразків градуювального набору. У спектрометрах типу ІнфраЛЮМ ФТ-10 виміряні спектри зразків проходять наступну процедуру нормалізації, яка враховує особливості приладів, які працюють на пропущення та використовують принципи Фур'є-спектроскопії. Обчислюється спектр, усереднений по всьому градуювальному наборі. (10) R = де N - число зразків у градуювальному наборі, j - порядковий номер довжини хвилі, на якій проводили виміри, R - виміряні спектральні дані для і-го зразка при j-ом значенні довжини хвилі Усереднений спектр віднімається від кожного спектра градуювального набору, так знаходяться середньозважені значення спектральних даних. (11) =R R Аналогічно знаходять середньозважені значення для референтних даних градуювальних зразків. Після знаходження середньозважених значень спектральні й референтні дані можуть бути піддані процедурі масштабування відхилень, при якій значення в кожній точці спектра ділиться на стандартне відхилення значень у цій точці по всьому градуювальному набору, де стандартне відхилення обчислюється по формулі. R (12) = В іншому варіанті попередньої математичної обробки спектральних даних проводять нормування спектрів по середньоквадратичному відхиленню. При цьому для кожного спектра із градуювального набору розраховується середнє арифметичне по всіх довжинах хвиль. (13) = де р - число довжин хвиль, при яких проводять виміри. Потім із значень у кожній спектральній точці вираховують середнє арифметичне й нормують отриману різницю на середньоквадратичне відхилення для даного спектра. R = (14) Якщо при процедурі нормалізації проводять вирівнювання базової лінії, тоді спектральні дані апроксимуються поліномом другого ступеня. у(х)=а1+а2х+а3х2 (15) записуючи вираження (15) у матричній формі одержуємо 25 86820 26 b=a·X (18) SECV= (16) b= Коефіцієнти апроксимації обчислюються за формулою. A=(XT*X)-1*Xt* де Xt - транспонована матриця X. Після знаходження коефіцієнтів апроксимації в кожній спектральній точці віднімається відповідне значення апроксимуючого полінома. Після здійснення процедури нормалізації результатів спектральних вимірів отримані спектральні дані зіставляються з відомими, які також пройшли нормалізацію, властивостями зразків градуювального набору, звідки знаходяться математичні співвідношення між спектральними даними й властивостями зразків, відомими з референтного аналізу. Дані співвідношення визначають градуювальну модель для опорного приладу. Як ми вже відзначали раніше, вид математичної обробки спектральних даних при нормалізації вибирається на підставі того, наскільки точно створена при даному виді обробки даних градуювальна модель передбачає властивості невідомого зразка, а в якості критерії точності використовуються статистичні параметри градуювальної моделі. Одним з таких параметрів є стандартна помилка калібрування (SEC), що дає оцінку наскільки властивості зразків, передбачені виходячи зі спектральних вимірів за допомогою даної градуювальної моделі, узгоджуються із властивостями, визначеними референтним методом. SEC= (17) де eі=ỹ-уi - помилка градировки для і-того зразка градуювального набору, ỹi -передбачені властивості, Уi - властивості, визначені референтним методом, d=N-k - число ступенів свободи градуювальної моделі, N - число градуювальних зразків, k - число перемінних величин у градуювальній моделі, яке залежить від математичного методу с, що використовується для побудови моделі. Для оцінки стійкості моделі проводять процедуру валідації [1]. Стандартна помилка кросвалідації (SECV) дозволяє оцінити максимальне число ступенів свободи, які повинні бути використані при створенні моделі. Для оцінки SECV один або більше градуювальних зразків видаляють з матриці спектральних даних і створюють модель без цих зразків. Потім створену модель використовують, щоб оцінити властивості, що аналізуються, вилучених зразків. Процес повторюють доти, поки кожний зразок із градуювального набору не виключать хоча б один раз. де - вектор, що містить оцінки перехресної валідації. Валідація за додатковим набором визначається параметром стандартної помилки валідації (SEV), який характеризує відхилення від референтних значень при аналізі зразків додаткового набору. (19) SEV= де dv - загальне число референтних значень параметра, що аналізується, для всіх спектрів додаткового набору, j - референтні значення аналізованого компонента для і-го спектра додаткового набору - передбачені значення аналізованого компонента для і-ro спектра додаткового набору. Основні характеристики вихідної градировки, створеної за 145 зразками продовольчої пшениці на опорному приладі, наведені в Таб.1. Таблиця 1 Результати градировки опорного приладу показник протеїн клейковина стекло волога SEC 0.41 0.62 2.56 0.19 SECV 0.41 0.69 2.74 0.20 SEV 0.34 0.65 2.37 0.25 Для створення нових незалежних градуювальних моделей на градуйованих приладах необхідно мати набір зразків для переносу. В експериментах з градуювального набору було відібрано кілька зразків. Однак відзначимо, що зразки в наборі для переносу в загальному випадку можуть не належати градуювальному набору. Було обрано два окремих набори для переносу. Перший набір підбирався на підставі параметра score [8], тобто із градуювального набору вибиралися зразки з максимальним і мінімальним значеннями параметра для будь-якого показника (наприклад, протеїну). Кращій перенос градировок досягається, коли до цих зразків додаються ті, які мають крайні значення scores і за іншими показниками (наприклад, для вологості й клейковини). Було обрано 10 зразків для переносу, які використовувались для побудови незалежних градуювальних моделей на 14 приладах. У другому випадку зразки вибиралися так, щоб їх референтні дані були рівномірно розподілені по всьому діапазоні. У цьому випадку для створення незалежних градуювальних моделей достатньо 27 86820 10-16 зразків. Уданому варіанті був проведений перенос спектральних даних градуювального набору з опорного приладу на п'ять градуйованих приладів по протеїну й клейковині. При кількості зразків менше 10 або більше 20 значення SEV для нових градировок погіршувалося. Відповідно до способу, який заявляється, ті самі зразки для переносу градировок вимірялись на всіх градуйованих приладах. Після чого, шляхом кореляції спектральних даних опорного й градуйованого приладів знаходились вираження для перетворення результатів спектральних вимірів на опорному приладі у вид градуйованих приладів. Характерною рисою спектрометрів ІнфраЛЮМ ФТ10, які використовують принцип Фур'є - спектроскопії, є те, що через конструктивні особливості приладів вимірювані спектри мають однакові постійні значення довжин хвиль (хвильових чисел) при яких проводяться виміри, що забезпечується синхронізуючим лазером [8]. Цей факт значно спрощує спосіб знаходження математичних спів 28 відношень для перетворення спектральних даних виміряних на опорному приладі у вид еквівалентний результатам вимірів на градуйованому приладі. У найпростішому виді ці співвідношення можуть бути визначені методом лінійної регресії, шляхом зіставлення результатів виміру спектральних даних для зразків з набору для переносу градировок, зроблених на опорному й градуйованому приладах. Rsi,j= а1i+a"iRm i,j (20) де Rsi,j - значення спектральних даних виміряні на градуйованому приладі (і-а довжина хвилі, j-й зразок з набору для переносу градировок), Rmi,j аналогічні спектральні дані, виміряні на опорному приладі. Спектральні дані можуть піддаватися процедурі нормалізації (попередній математичній обробці), однак повністю однаковим перетворенням, як для опорного так і для градуйованого приладів. Коефіцієнти регресії визначаються методом найменших квадратів. a' = a'' = де с - кількість зразків у наборі для переносу градировок. Після знаходження коефіцієнтів регресії спектральні дані для кожного зразка із градуйованого набору перетворюються у вид відповідний вимірам на градуйованому приладі. Далі створюється нова градуйована модель за перетвореними даними градуйованого набору. Створена незалежна модель на кожному градуйованому приладі проходила стандартну процедуру валідації [1], де визначалися основні статистичні параметри градуйованої моделі. У таблиці 2 наведені дані по створенню градировок для продовольчої пшениці, отримані з вико ристанням 10 зразків для переносу, обраних на підставі параметра score для 14 градуйованих приладів. Отримані результати демонструють високу точність передбачення властивостей невідомого зразка при використанні способу створення незалежних градуювальних моделей, що заявляється. На закінчення ще раз відзначимо, що галузь застосування способу, що заявляється, не обмежується Фур'є-спектроаналізаторами або спектрометрами іншого типу. Запропонована ідеологія може бути застосована до різних приладів, де одні властивості зразка визначаються з багаторазового виміру інших властивостей. Таблиця 2 Результати створення градировок за зразками для переносу, обраними виходячи з параметра SCORE Компонент Протеїн Номер приладу Номер зразка 470 471 472 473 474 475 476 477 478 479 SEV реф. знач. 13.94 13.29 12.66 12.53 13.11 13.86 12.01 13.06 12.28 12.78 прилад майстер 14.09 13.89 12.88 12.62 12.71 14.17 12.06 13.55 12.61 12.60 0.34 1 2 3 4 5 6 14.07 14.11 12.90 12.72 13.15 14.27 12.40 13.62 12.71 12.85 0.31 13.83 13.74 12.55 12.61 12.75 13.90 12.21 13.41 12.41 12.44 0.29 13.88 13.83 12.57 12.40 12.71 13.98 11.82 13.38 12.43 12.52 0.31 * 13.94 12.64 12.48 12.83 13.87 12.17 13.36 12.30 12.38 0.33 * 13.82 12.76 12.29 12.79 13.88 12.08 13.60 12.61 12,51 0.38 14.09 14.05 12.72 12.59 12.98 14.13 12.33 13.59 12.69 12.73 0.33 29 86820 30 Продовження таблиці 2 Клейковина Скловидність Вологість Компонент Протеїн Клейковина 470 471 472 473 474 475 476 477 478 479 SFV 470 471 472 473 474 475 476 477 478 479 SFV 470 471 472 473 474 475 476 477 478 479 SEV Номер приладу Номер зразка 470 471 472 473 474 475 476 477 478 479 SEV 470 471 472 473 474 475 476 477 478 479 SEV 23.60 23.90 20.00 19.10 20.00 23.80 17.80 21.60 19.30 18.70 7 23.29 23.03 20.41 18.49 20.30 23.62 18.96 22.44 19.18 19.05 0.65 49.96 50.72 49.06 45.71 49.05 50.64 48.24 50.90 47.27 46.58 2.37 11.03 11.06 10.91 11.48 10.89 11.09 11.41 10.76 11.71 11.82 0.25 8 22.96 23.00 20.33 18.98 20.81 23.48 19.05 21.99 18.87 19.08 0.82 49.39 49.80 47.65 46.57 48.15 50.28 47.48 49.75 46.17 45.78 2.30 10.92 10.96 10.96 11.31 10.80 11.04 11.37 10.78 11.55 11.66 0.33 9 23.15 22.65 19.88 19.28 20.53 23.46 19.25 22.18 18.87 18.62 1.14 49.81 49.11 47.82 46.68 48.60 50.56 47.97 50.22 46.61 46.00 2.36 11.04 11.08 10.98 11.42 10.88 11.12 11.35 10.71 11.63 11.88 0.25 10 23.57 23.24 20.42 18.98 20.51 23.63 18.45 22.21 19.17 19.16 0.72 50.32 50.05 48.29 45.94 48.59 50.58 46.85 50.28 47.51 45.81 2.41 10.94 11.01 10.94 11.36 10.85 11.07 11.43 10.74 11.59 11.77 0.30 11 * 23.70 20.38 19.22 21.18 23.65 19.31 22.13 19.05 18.88 0.76 * 50.59 48.20 46.70 48.50 50.09 48.10 50.29 47.37 46.27 2.36 * 10.99 10.96 11.48 10.85 11.15 11.38 10.83 11.73 11.86 0.21 12 * 23.26 20.60 18.28 20.83 23.45 19.05 22.63 19.77 19.01 0.65 * 50.21 48.48 45.09 48.92 51.16 48.11 50.87 47.64 46.06 2.82 * 11.04 10.95 11.50 10.91 11.12 11.41 10.69 11.63 11.82 0.21 13 13.98 14.29 12.82 12.82 13.02 14.28 12.38 13.60 12.74 12.89 0.44 22.57 23.54 20.13 18.93 20.30 23.50 18.84 21.82 18.58 19.01 0.68 13.98 14.09 12.78 12.58 12.82 13.99 12.02 13.58 12.76 12.63 0.35 23.15 23.20 20.27 18.73 20.08 23.22 18.38 21.96 19.13 18.76 0.69 14.11 14.24 12.86 12.75 13.04 14.17 12.04 13.69 12.76 12.71 0.48 23.09 23.21 20.16 18.87 20.51 23.17 17.99 22.17 19 00 18.74 0.64 14.13 14.14 12.74 12.75 13.04 14.12 12.08 13.76 12.81 12.82 0.42 23.68 23.55 20.26 18.88 20.91 23.45 18.54 22.97 19.56 19.24 0.65 14.16 14.12 12.75 12.82 13.09 14.28 12.23 13.68 12.85 12.86 0.45 23.26 23.07 19.84 18.99 20.70 23.49 18.58 22.27 19.31 19.12 0.65 14.27 14.24 12.70 12.69 13.02 14.29 12.24 13.73 12.68 12.81 0.45 23.33 23.22 19.76 18.62 20.39 23.42 18.60 22.13 18.61 19.00 0.60 14.21 14.12 14.16 14.11 12.82 12.76 12.79 12.68 13.04 13.05 14.16 14.25 12.30 12.27* 13.64 12.65 12.67 12.84 12.91 0.40 0.51 23.36 23.39 23.17 23.46 19.74 19.85 19.04 19.75 20.56 20.40 23.15 23.71 18.62 18.57 22.07 * 18.49 19.48 19.12 20.19 0.70 0.65 50.00 50.00 47.00 45.00 46.00 50.00 50.00 45.00 47.00 48.00 11.50 11.00 11.00 11.50 11.00 11.00 11.00 10.50 12.00 12.00 23.47 23.32 20.18 18.90 20.80 23.48 19.27 22.14 19.16 19.19 078 49.74 50.09 48.11 46.19 48.38 49.76 47.98 49.70 46.79 46.13 2.06 10.95 11.01 10.98 11.33 10.88 11.06 11.33 10.73 11.60 11.74 0.28 14 31 86820 32 Продовження таблиці 2 Скловидність Вологість 470 471 472 473 474 475 476 477 478 479 SEV 470 471 472 473 474 475 476 477 478 479 SEV 49.29 50.47 48.74 46.19 48.49 50.26 47.48 50.49 45.55 45.45 2.49 11.08 10.95 10.90 11.29 10.78 11.02 11.29 10.72 11.58 11.65 0.28 50.22 50.31 48.14 46.44 47.88 50.23 47.63 49.80 46.98 45.90 2.18 10.97 10.99 10.99 11.38 10.82 11.07 11.42 10.77 11.62 11.75 0.28 50.25 50.30 48.23 46.09 48.40 50.33 46.85 50.44 46.87 45.38 2.54 10.98 11.00 10.89 11.33 10.81 10.98 11.36 10.74 11.51 1171 0.31 50.85 50.04 48.16 46.43 49.01 50.43 47.31 50.80 47.18 45.85 2.58 10.95 10.97 11.03 11.35 10.80 11.04 11.38 10.75 11.61 11.72 0.30 50.38 50.07 48.17 46.47 48.87 50.45 47.46 50.42 46.81 46.18 2.54 10.96 10.99 10.90 11.33 10.82 11.01 11.36 10.71 11.55 11.71 0.31 50.21 50.18 48.11 46.14 47.95 50.46 47.42 49.99 46.14 45.94 2.36 10.89 10.94 10.87 11.35 10.71 10.99 11.27 10.65 11.45 11.61 0.36 50.28 50.20 47.82 46.65 48.29 49.97 47.37 50.57 45.99 45.35 2.41 10.96 10.80 10.85 11.34 10.73 11.04 11.32 10.67 11.40 11.55 0.36 51.21 50.76 49.03 46.61 48.66 51.38 48.22 * 47.08 45.22 2.00 11.09 11.16 11.09 11.48 11.22 11.11 11.46 * 11.51 11.51 0.35 * Реєстрація спектра не проводилася. Джерела інформації: 1. ASTM standard, E 1655 - 00, Practices for Infrared Multivariate Quantitative Analysis. 2. Патентна заявка США № 4 944 589, МПК G01J3/18, опублікована 31.07.1990 3. Патентна заявка США № 6 615 151, МПК G01N015/06, опублікована 02.09 2003 4. Патентна заявка США № 4 866 644, МПК G01N37/00, опублікована 12.09.1989 5. Патентна заявка США № 5 459 677, МПК G01N021/01, опублікована 17.10.1995 6. Європейська патентна заявка ЕР 0 663 997 В1, МПК G01N021/27, опублікована 17.10.1995 . 7. Патентна заявка США № 5 347 475, МПК G01J003/02, опублікована 13.09.1994 8. Посібник з експлуатації ІнфраЛЮМ ФТ-10, 152.00.00.00.РЭ. 33 Комп’ютерна верстка Н. Лисенко 86820 Підписне 34 Тираж 28 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601