Спосіб розрахунку координат об’єктів на поверхні моделі очного яблука
Номер патенту: 37269
Опубліковано: 25.11.2008
Автори: Ємченко Віктор Іванович, Мосьпан Владислав Олександрович, Кухаренко Дмитро Володимирович
Формула / Реферат
Спосіб розрахунку координат об'єктів на поверхні моделі очного яблука, який включає визначення сферичних координат на моделі, яка являє собою сферу з визначеним радіусом у відповідності з виразами:
![]() ,
,
![]() ,
,
![]() ,
,
де r - радіус сфери,
x,y,z - декартові координати,
j і q - сферичні координати сфери,
який відрізняється тим, що в комп'ютер вводять такі дані: радіус ока і сферичні координати точки на поверхні моделі очного яблука, і визначають координати об'єктів на поверхні моделі очного яблука у відповідності з виразами:
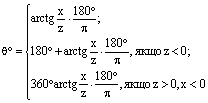
![]()
Текст
Спосіб розрахунку координат об'єктів на поверхні моделі очного яблука, який включає визначення сферичних координат на моделі, яка являє собою сферу з визначеним радіусом у відповідності з виразами: 2 3 37269 координат анатомічних утворень на поверхні моделі очного яблука, використовуючи ОССК. Це досягається тим, що використовують мову високого рівня програмування Delphi 7 і відповідний математичний апарат. Спільними ознаками найближчого аналога та корисної моделі є визначення сферичних координат на моделі, яка представляє собою сферу з визначеним радіусом. Корисна модель відрізняється тим, що в комп'ютер вводять дані: радіус ока, а також при необхідності розрахунку декартових координат анатомічних утворень і сферичні координати. Визначають координати об'єктів на поверхні моделі очного яблука у відповідності з виразами: x 180° ì ïarctg z × p ; ï x 180° ï q ° = í180° + arctg × , якщ о z 0, x < 0 î j° = arctg x 180 ° × , z p де x, y, z - декартові координати. На Фіг. представлений спосіб розрахунку координат об'єктів на поверхні моделі очного яблука. Спосіб здійснюють наступним чином: запускають файл визначення координат. В першу чергу вводять у вікно під номером 17 радіус моделі ока в міліметрах, якщо цього не зробити, не буде здійснений процес розрахунку відстані між точками М і М¢ по дузі і по хорді в міліметрах. Спосіб дозволяє здійснювати процес обертання моделі ока у тривимірній декартовій системі координат за допомогою колеса миші. Для цього необхідно натиснути колесо миші на поверхні моделі очного яблука і, переміщуючи мишу в ту чи іншу сторону модель ока буде обертатися навколо осей тривимірної декартової системи координат. Також спосіб передбачає кнопки керування, які знаходяться на робочому вікні 22-30. Кнопкою 22 - здійснюють обертання моделі ока справа наліво. Щоб модель ока постійно рухалася, лівою клавішею миші утримують необхідну кнопку до ти х пір поки модель ока не буде у потрібному положенні. Кнопкою 27 здійснюють обертання ока зліва направо, 24 - зменшують модель ока, 25 - збільшують, 26 - виконують переміщення моделі ока в початкове поло 4 ження, 28 - виконують обертання ока навколо осі Y проти годинникової стрілки, 30 - виконують обертання ока навколо осі Y за годинниковою стрілкою, 23 - виконують обертання ока знизу вверх, 29 зверху вниз. Обертаючи модель ока навколо осей тривимірної декартової системи координат, знаходять м'яз, який необхідно оперувати шляхом пересадження в інше місце на поверхні моделі очного яблука. Далі в робочому вікні за допомогою лівої клавіші миші встановлюють фіксовану точку М, яка має червоний колір, на поверхню моделі очного яблука, а саме на той м'яз, який необхідно пересадити. Правою клавішею миші встановлюють другу фіксовану точку М¢, яка має жовтий колір, на поверхню моделі очного яблука, на те місце, де планується розташувати пересаджений м'яз. У вікнах під номером 13 і 14 відобразяться числові дані відстані між точками по хорді і по дузі у відносних одиницях і в міліметрах у вікнах 15, 16. При переміщенні фіксованих точок по поверхні моделі очного яблука відповідні декортові (1, 2, 3 - для точки М і 4, 5, 6 - для точки М¢) і сферичні (довгота: 18-М, 20-М¢; широта: 19-М, 21-М¢) координати змінюються в відповідності до величини переміщення. Спосіб також включає розрахунок кута поворота навколо кожної з осей тривимірної декартової системи координат Х(7), Y(8), Z(9). Для цього достатньо поставити фіксовані точки М і М¢ на поверхню моделі очного яблука. Розрахунок декартових координат точки М проводять наступним чином: у вікна 10 і 11 вводять сферичні координати: довгота і широта відповідно. При натисканні лівої клавіші миші на кнопку розрахунок (12) проводиться автоматичне визначення декартових координат x, y, z (31, 32, 33) точки М і її розташування на поверхні моделі очного яблука. При цьому модель ока повертається до оператора таким чином, щоб він зміг візуально спостерігати місце розташування фіксованої точки М. Технічний результат способу полягає у скороченні часу на проведення досліджень, точно відображає окорухові стр уктури очного яблука людини. Спосіб тривимірного моделювання зміни координат прикріплень окорухови х м'язів на поверхні моделі очного яблука може використовуватись в офтальмології для підвищення ефективності хірургічни х операцій. 5 Комп’ютерна в ерстка C.Литв иненко 37269 6 Підписне Тираж 28 прим. Міністерство осв іт и і науки України Держав ний департамент інтелектуальної в ласності, вул. Урицького, 45, м. Київ , МСП, 03680, Україна ДП “Український інститут промислов ої в ласності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for calculating coordinates of objects on surface of eyeball model
Автори англійськоюKukharenko Dmytro Volodymyrovych, Mospan Vladyslav Oleksandrovych, Yemchenko Viktor Ivanovych
Назва патенту російськоюСпособ расчета координат объектов на поверхности модели глазного яблока
Автори російськоюКухаренко Дмитрий Владимирович, Мосьпан Владислав Александрович, Емченко Виктор Иванович
МПК / Мітки
МПК: G09B 23/00, A61B 3/00
Мітки: моделі, розрахунку, яблука, об'єктів, спосіб, координат, очного, поверхні
Код посилання
<a href="https://ua.patents.su/3-37269-sposib-rozrakhunku-koordinat-obehktiv-na-poverkhni-modeli-ochnogo-yabluka.html" target="_blank" rel="follow" title="База патентів України">Спосіб розрахунку координат об’єктів на поверхні моделі очного яблука</a>
Попередній патент: Пневматичний висівний апарат
Наступний патент: Спосіб зниження частоти коливального процесу
Випадковий патент: Спосіб виробництва напоїв вітамінізованих "топіфрут-яблуко"







