Спосіб виміру частоти гармонійних коливань
Номер патенту: 66357
Опубліковано: 26.12.2011
Формула / Реферат
Спосіб виміру частоти гармонійних коливань, що включає операції аналого-цифрового перетворення сигналу, запам'ятовування його значень в N наступних моментах часу, який відрізняється тим, що операцію аналого-цифрового перетворення сигналу здійснюють за синхронною квадратурною схемою з рівномірною дискретизацією, а оцінку частоти гармонійних коливань розраховують за сукупністю з N відліків кожної з квадратурних складових напруг сигналів згідно з виразом:
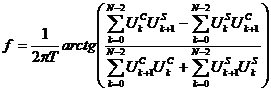 ,
,
де ![]() ,
, ![]() та
та ![]() ,
, ![]() - косинусна і синусна квадратурні складові напруг сигналів у k-му та k+1-му часових відліках,
- косинусна і синусна квадратурні складові напруг сигналів у k-му та k+1-му часових відліках, ![]() - період дискретизації.
- період дискретизації.
Текст
Спосіб виміру частоти гармонійних коливань, що включає операції аналого-цифрового перетворення сигналу, запам'ятовування його значень в N наступних моментах часу, який відрізняється тим, що операцію аналого-цифрового перетворення сигналу здійснюють за синхронною квадратур ною схемою з рівномірною дискретизацією, а оцінку частоти гармонійних коливань розраховують за сукупністю з N відліків кожної з квадратурних складових напруг сигналів згідно з виразом: N 2 N 2 C S S C Uk Uk 1 Uk Uk 1 k 1 k 0 f arctg N 0 , 2 N 2 2Т UC UC US US k 1 k k 1 k k 0 k 0 Корисна модель відноситься до вимірювальної техніки й може бути використана для виміру відхилень миттєвої частоти від номінального значення, для демодуляції частотно-модульованих сигналів у радіовимірювальних, радіоприймальних пристроях, у цифрових телевізійних декодерах СЕКАМ та радіолокації. Відома значна кількість способів демодуляції дискретного частотно-модульованого сигналу, виміру частоти гармонійних коливань, докладний огляд яких наведений, наприклад, в [1]. Один з найбільш простих способів полягає в тому, що для обчислення значень миттєвої частоти в ньому використовуються три послідовні вибірки сигналу, наприклад А1 А2 і А3, на підставі яких визначають частоту відповідно до виразу [1]: A A3 1 arccos 1 (1) Т 2A 2 , де Т - період дискретизації. Можна показати, що даний спосіб оцінювання є оптимальним за мінімумом середньоквадратичної похибки виміру. Використана в ньому операція ділення на вибірку А2 зменшує залежність вихідного сигналу від амплітуди несучої, тобто деякою мірою замінює амплітудний обмежник, що особливо важливо для демодуляції частотномодульованих сигналів. Разом з тим наявність операції ділення в розглянутому способі є його недоліком, оскільки при А2 = 0 виконати її неможливо. Розвитком даного підходу до виміру частоти є спосіб [2], що включає, зокрема, операції аналогоцифрового перетворення сигналу, запам'ятовування його значень в N послідовних одна за одною тріадах моментів часу, спільну обробку всіх отриманих тріад відліків аналого-цифрового перетворення. Слід зазначити, що підсумовування кількох тріад відліків сигналу дозволило знизити вплив флуктуаційних завад. Крім того, у розглянутому способі вдалося виключити можливість збоїв, обумовлених діленням на нуль, хоча для цього й треба було ввести операцію логарифмування. Недоліком відомого способу [2] є не оптимальність обробки відліків напруг сигналу (використовуються не самі напруги, а їхні модулі). Крім того, у розглянутому способі, щоб уникнути зсуву нульової точки аналого-цифрового перетворювача АЦП, необхідно виконувати додаткове зважування цифрових відліків сигналів. Найбільш близьким за технічною сутністю до винаходу, що заявляється, є спосіб виміру частоти гармонійних коливань [3], що включає операції аналого-цифрового перетворення сигналу, запам'ятовування його значень в N наступних момен (19) UA (11) 66357 (13) U C C S S де Uk , Uk 1 та Uk , Uk 1 - косинусна і синусна квадратурні складові напруг сигналів у k-му та k+1му часових відліках, Т - період дискретизації. 3 66357 тах часу, який полягає в тому, що частоту сигналу визначають відповідно до виразу: f 1 1 arccos 2Т 2 N U 2n n1 N , U1n U3n U2n 2 n1 1 (2) де Т - інтервал дискретизації АЦП, U1n, U2n, U3n - напруги першого, другого і третього відліків, що оброблюються в n-му положенні ковзного вікна, N кількість трійок відліків, що усереднюються (загальна кількість зсувів вікна обробки), причому вибір частоти дискретизації сигналу, розміщення тріад у часі й вибір їхньої кількості здійснюють за умови 4 S Uk A sinТk , (6) де С і S - синфазна й квадратурна складові, відповідно. Розглянемо наступні суми відліків напруг на виходах АЦП: C C C S Uk Uk 1 1 cosТ Uk sinТ Uk . (7) S S S C Uk Uk 1 1 cosТ Uk sinТ Uk . (8) Перепишемо вирази (7) і (8) у вигляді C C S Uk 1 Uk Uk 0 N (9) U2n 2 n 1 нерівності нулю суми . Спосіб-прототип дозволяє оптимально, за методом найменших квадратів, оцінити частоту гармонійних коливань по серії цифрових відліків напруг сигналів. Недоліком способу-прототипу є неможливість його використання для виміру частоти сигналів, представлених у комплексній формі запису, тобто таких, що мають квадратурні складові напруг. З урахуванням сказаного, технічне завдання, що вирішується заявленою корисною моделлю, полягає у забезпеченні оптимального виміру частоти гармонійних коливань сигналу у комплексній формі запису, представленого сукупністю цифрових відліків квадратурних складових напруг. Сутність корисної моделі полягає в тому, що на відміну від прототипу операцію аналогоцифрового перетворення сигналу здійснюють за синхронною квадратурною схемою з рівномірною дискретизацією, а оцінку частоти гармонійних коливань розраховують за сукупністю з N відліків кожної з квадратурних складових напруг сигналів згідно з виразом: N 2 N 2 C S S C Uk Uk 1 Uk Uk 1 k 0 1 k 0 f arccos N2 N 2 2Т UC UC US US k 1 k k 1 k k 0 k 0 , (3) F C C S Uk 1 Uk Uk N2 2 (5) S S C Uk 1 Uk Uk N2 2 min (11) . Мінімізуємо значення функції F. Прирівнявши похідні F по μ і ν нулю й вирішуючи отриману систему рівнянь, одержимо оцінки μ і ν: k 0 N 2 N 2 k 0 N 2 k 0 N 2 U C 2 Uk N 2 k 0 C C S S Uk 1Uk Uk 1Uk k 0 k 0 (12) S 2 k , N 2 C S S C Uk Uk 1 Uk Uk 1 k 0 N 2 k 0 N 2 U C 2 Uk k 0 S 2 k (13) Остаточна оцінка частоти ω має вигляд де А - амплітуда сигналу; ω=2 - кругова частота вхідного сигналу; φ - початкова фаза вхідного сигналу. Нехай сигнал (4) рівномірно дискретизирується за допомогою синхронно тактовних аналогоцифрових перетворювачів (АЦП) із періодом дискретизації Т. Зневажаючи шумами, запишемо вирази для k-го відліку синфазної й квадратурної складових напруг на виходах АЦП: (10) де μ = cos(ωТ) й ν = sin (ωТ). Для оцінки частоти ω скористаємося методом найменших квадратів. Нехай отримана вибірка з N відліків. Використовуючи вирази (9) і (10), запишемо цільову функцію у вигляді k 0 C C S S де Uk , Uk 1 та Uk , Uk 1 - косинусна і синусна квадратурні складові напруг сигналів у k-му та k + 1-му часових відліках. Запропонований спосіб дозволяє оптимально оцінити частоту гармонійних коливань, для доведення чого слід скористатися ідеями, викладеними в [1]. Нехай на вході АЦП є присутнім гармонійний комплексний сигнал виду иt A expjt , (4) C Uk A cosТk , S S C Uk 1 Uk Uk 0 , 1 arctg Т . (14) Використовуючи результати (12) і (13), перепишемо вираз (14) у наступному виді N 2 N 2 C S S C Uk Uk 1 Uk Uk 1 k 0 1 k 0 arctg N 2 (15) N 2 Т С UC US US k 1 k k 1 k k 0 k 0 , що відповідає виразу (3). Для підтвердження можливості реалізації способу, що заявляється, був використаний спеціальний модуль цифрової обробки сигналів з двома синхронними АЦП, що дозволяє оцифровувати радіочастотний сигнал (безперервний або імпульсний) за квадратурною схемою, накопичувати його дискретні відліки в буферному оперативному запам'ятовуючому пристрої (ОЗП) в темпі їхнього надходження й далі через системну шину завантажувати отримані відліки напруг сигналів для обробки у ПЕОМ. Крім того, працездатність заявленого способу була доведена шляхом моделювання його операцій у пакеті Mathcad. 5 Джерела інформації: 1. Хохлов Б. Н. Декодирующие устройства цветных телевизоров. - М.: Радио и связь, 1992.-С. 88-101. 2. Хохлов Б. Н. Декодирующие устройства цветных телевизоров. - М.: Радио и связь, 1992.-С. 97-101. Комп’ютерна верстка Л. Купенко 66357 6 3. Патент РФ № 2111496, G01R23/00. Способ измерения частоты гармонических колебаний. // Слюсар В. И., Покровский В. И., Сахно В. Ф., Слюсарь И. И. - Опубл. 20.05.98, Бюл. № 14. - прототип. Підписне Тираж 23 прим. Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for measurement of frequency of harmonic vibrations
Автори англійськоюBondarenko Maksym Vasyliovych, Sliusar Vadym Ivanovych
Назва патенту російськоюСпособ измерения частоты гармонических колебаний
Автори російськоюБондаренко Максим Васильевич, Слюсар Вадим Иванович
МПК / Мітки
МПК: G01R 23/00
Мітки: коливань, спосіб, гармонійних, виміру, частоти
Код посилання
<a href="https://ua.patents.su/3-66357-sposib-vimiru-chastoti-garmonijjnikh-kolivan.html" target="_blank" rel="follow" title="База патентів України">Спосіб виміру частоти гармонійних коливань</a>
Попередній патент: Моноблок дрібнобульбашкового продування для ливарних і проміжних ковшів
Наступний патент: Спосіб додаткового стробування цифрових відліків сигналів
Випадковий патент: Засіб підвищення зносостійкості покриттів високотемпературного призначення







