Спосіб визначення граничного значення стискуючого навантаження деталі
Номер патенту: 39527
Опубліковано: 25.02.2009
Формула / Реферат
Спосіб визначення граничного значення стискуючого навантаження деталі, що включає операції визначення схеми навантажування, при якій жорсткість деталі є мінімальною, подальшого навантажування деталі стискуючим зусиллям і її одночасного навантажування за визначеною схемою, при якій жорсткість деталі є мінімальною, під час якого реєструють лінійну деформацію деталі в ділянці, де прикладають зусилля за схемою, при якій жорсткість деталі є мінімальною, і визначають зміну жорсткості деталі в згаданій ділянці, за якими визначають граничне значення стискуючого навантаження деталі з виразу:
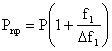 ,
,
де f1 - деформація деталі в ділянці, де прикладають зусилля за схемою, при якій жорсткість деталі є мінімальною без навантажування деталі стискуючим зусиллям; Df1 - зміна деформації f1 під час навантажування деталі стискуючим зусиллям Р.
Текст
Спосіб визначення граничного значення стискуючого навантаження деталі, що включає операції визначення схеми навантажування, при якій жорсткість деталі є мінімальною, подальшого навантажування деталі стискуючим зусиллям і її одночасного навантажування за визначеною схемою, при якій жорсткість деталі є мінімальною, під час 3 39527 значають граничне значення стискуючого навантаження Рnр деталі з виразу: æ f ö Pnp = Pç 1+ 1 ÷ , ç Df1 ÷ è ø де f1 - деформація деталі в ділянці, де прикладають зусилля за схемою, при якій жорсткість деталі є мінімальною без навантажування деталі стискуючим зусиллям; Df1 - зміна деформації f1 під час навантажування деталі стискуючим зусиллям Р. Особливістю пропонованого способу є те, що для визначення граничного навантаження деталей визначають зміну жорсткості частини деталі, матеріал якої частково руйнується при навантаженнях, значення яких є менші за граничні. Для цього виготовляють зразок, який має такий самий концентратор (тріщину), форму і схему навантаження, що і досліджувана деталь, але значно менших розмірів. Такий зразок має меншу жорсткість і змінюється вона поступово (більш в'язко). Деталь змінює жорсткість раптово (більш крихко) при інших станах матеріалу і значеннях критеріїв міцності. Впливає масштабний фактор. По зміні жорсткості зразка розміром R0 рахують граничні напруження і переміщення в деталі розміром r за формулами æ G Rn -1 ö Gu ç 2 0 G ÷ s = 1 0 +ç - 1 ÷ ò f (u0 )du0 , R0 R0 ÷ ç rn è ø æ n -1 ö u u0 ç R0 1 ÷ = +ç f (u )du0 , r R0 ç rn R0 ÷ò 0 ÷ è ø де G1 и G 2 - коефіцієнти пружності, що залежать від матеріалу і схемі навантаження, E (n - 1)E G1 = , G2 = - модуль пружності 1- (n - 1)m (1+ m ) матеріалу, m - коефіцієнт Пуассона; n - параметр, що залежить від форми деталі, визначається експериментально, функція f(u0) дорівнює G0 (u0 ) - G1 f (u0 ) = , G0(u0) - жорсткість зразка, u0 G2 - G1 переміщення зразка. Під час використання пропонованого способу можуть бути використані такі схеми навантаження, при яких жорсткість досліджуваної деталі є мінімальною. Жорсткість деталі, форма якої є близької до стрижня постійної товщини при шарнірному закріпленні мінімальна, якщо силу прикласти посередині довжини деталі перпендикулярно до неї. При жорсткому закріпленні одного кінця деталі, жорсткість мінімальна, якщо силу прикласти до вільного кінця деталі, перпендикулярно до неї в напрямку мінімального моменту інерції її поперечного перерізу, якщо подовжнє стискаюче навантаження прикладене в центрі цього перетину. Якщо навантаження істотно зміщене від центру в напрямку максимального моменту інерції (перпендикулярно напрямкові мінімального моменту інерції), то схемою прикладання сил, при якій жорсткість деталі мінімальна, буде прикладання сили в напрямку 4 максимального моменту інерції. У випадку довільного зсуву навантаження щодо центра ваги перетину напрямок дії сили, що відповідає мінімальної жорсткості знаходиться між напрямком зсуву і напрямком мінімального моменту інерції. Для тонкостінної деталі незамкнутого профілю (швелер, двотавр, подовжньо розрізаний короб), схемою прикладання сил, при якій жорсткість деталі мінімальна буде прикладання моменту, що скручує. У загальному випадку схема прикладання сил, при якій жорсткість деталі мінімальна, визначається експериментально, послідовною перевіркою найбільш очевидних комбінацій схем. Вимога мінімальності жорсткості не є суворою. Не є обов'язковим вимірювати жорсткість при схемі, що відповідає найменшої жорсткості. Важливо лише, щоб жорсткість була істотно менша за жорсткість деталі при схемі прикладання основного навантаження і змінювалася більш лінійно, щоб її зміну можна було б надійно вимірити при навантаженнях припустимо менших за граничні. Приклад. Для обґрунтування можливості виміру змін жорсткості і розрахунку граничного стискаючого навантаження, при якій жорсткість мінімальному і відповідному основному навантаженню стає рівної нулеві, розглянемо найбільш простий випадок розрахунку зміни цих жорсткостей. Найбільш простим є випадок, коли форма деталі близька до форми стрижня постійної товщини, що шарнірно закріплений на кінцях і стискується подовжнім навантаженням. Його жорсткість Gпрод У подовжньому напрямку дорівнює EF Gпрод = , L де Е - модуль пружності матеріалу, F - площа поперечного переріза стрижня, L - довжина стрижня. Зі збільшенням подовжнього навантаження ця жорсткість змінюється дуже нелінійно. Спочатку вона практично не міняється, а поблизу граничного значення дуже швидко змінюється до нульових і від'ємних значень. Найменшу жорсткість стрижень має при схемі прикладання навантаження перпендикулярно стрижневі в його середині в напрямку мінімального моменту інерції поперечного переріза. При відсутності подовжньої сили ця жорсткість дорівнює: 48EJ G0 = , L3 де J - мінімальний момент інерції поперечного переріза стрижня. При впливі подовжнього навантаження Р поперечна жорсткість стрижня G змінюється по наступній залежності: G= G0 3 (KP )3 KP - th KP , L2 . При стискуючому 4EJ навантаженні, тобто від'ємних значеннях Р жорсткість G залишається дійсною. Уявна одиниця де K - параметр, K = i= - 1 скорочується. У діапазоні значень подовжнього навантаження від граничної до нульо 5 39527 вої відмінність цієї залежності від лінійної апрокæ P ö ÷ складає менш симації у вигляді G = G0 ç 1 ç Pпp ÷ è ø половини відсотка. Таким чином, зміна жорсткості при зміні подовжньої сили поблизу безпечно малих і граничних її значень практично однакова, що дозволяє по обмірюваній зміні мінімальної жорсткості розрахувати граничне значення подовжнього стискаючого навантаження, використовуючи лінійну апроксимацію. У більш складних випадках, а також при істотній відмінності схеми прикладання сил від схеми, при якій жорсткість деталі мінімальна, але помітно менше ніж при схемі прикладання основного навантаження, необхідно використовувати нелінійну залежність. Але тому що вона буде набагато більш плавної чим залежність жорсткості при схемі прикладання основного навантаження, то мається можливість досить точно оцінити її граничне значення по вимірах зміни жорсткості деталі в безпечному діапазоні значень навантаження. Приклад 1. Розглянемо простий випадок. Стрижень постійного перетину закріплений шарнірно на кінцях і стискується подовжнім навантаженням. Жорсткість стрижня мінімальна у випадку прикладання сили перпендикулярно стрижневі в його середині. Виміримо мінімальну жорсткість без прикладання навантаження. Для цього прикладемо силу, величиною Р1=1Н. Допустимо, стрижень прогнеться на f1=0,001м. У цьому випадку мінімальна жорсткість дорівнює P G0 = 1 = 1кН / м . f1 Навантажимо стрижень подовжнім стискаючим навантаженням величиною Р=1кН. При тій же силі Р1=1Н цього разу стрижень прогнеться більше f2=0,0011м. Мінімальна жорсткість стрижня зменшиться на величину P DG0 = G0 - 1 = 0,0909 кН / м . f2 Визначимо в скількох разів прикладена подовжня сила менше граничної. Для цього початкове значення мінімальної жорсткості G0 розділимо на її зміну при прикладанні сили Р=1кН. Pпp G = 0 = 11 . P DG0 Таким чином, граничне значення подовжньої стискаючої сили дорівнює: Рпр=11Р=11кН 2. Розглянемо складний випадок. Деталь складної форми має жорсткість при основній схемі прикладання сил рівну G=100кН/м. Методом проб знаходимо схему, при якій жорсткість деталі помітно менше. Наприклад, G0=4кН/м. Навантажимо деталь за основною схемою прикладання сил силою Р1=1кН і визначимо жорсткість при знайденій схемі прикладання сил. Наприклад, G01=3,98кН/м. Аналогічно визначимо жорсткість при знайденій схемі прикладання сил у випадку основного навантаження Р2=2кН. Наприклад, G02=3,94кН/м. Апроксимуємо залежність жорсткості (меншої, чим основний) деталі при знай 6 деній схемі прикладання сил нелінійною залежністю у виді полінома другого ступеня G0Р=A+ВP+CP2 . Коефіцієнти А, В и С визначаємо з рішення системи рівнянь: G0=A, при Р=0; G01=A+BP 1+CP12 ; при Р=Р1; G02=A+BР 2+СP22 ; при Р=P2, A=G 0=4кН; 2 2 2 2 G02P1 - G02P2 + A(P2 - P1 ) B= = - 0,01; 2 P1 P2 - P1 2 P2 G01 - A - BP1 = -0,01. 2 P1 Дорівнюючи поліном до нуля і вирішуючи квадратне рівняння щодо сили Р, одержимо граничне навантаження C= - B - B2 - 4AC = 19,50625к Н . 2C Враховуючи, що мінімальна жорсткість деталі в порівнянні з жорсткістю за експлуатаційною схемою змінюється більш плавно, її зміна при невеликих навантаженнях велика. Ця обставина сприяє її достовірному визначенню і коректному наступного розрахунку граничного навантаження. Приклад 2. Деталь значних габаритів має концентратор напруг, наприклад тріщину. Її жорсткість незначно змінюється аж до втрати стійкості деформування і втрати несучої здатності. Тобто має місце крихке руйнування. Жорсткість деталі зменшують шля хом видалення масивної, але найменш навантаженої частини деталі. Для виміру меншої жорсткості виготовляють деталь значно менших розмірів, що має такий же дефект. Схему прикладання сил вибирають близькою до тієї, що навантажує цю частину деталі при експлуатації досліджуваної деталі. Вимір жорсткості роблять на досить жорсткій установці, що дозволяє вимірювати негативні значення жорсткості на спадаючій ділянці повної діаграми деформування деталі. По зміні жорсткості малої деталі, використовуючи рівняння теорії пружності, розраховуємо зміну жорсткості, переміщень і сил у місці прикладання сил прогнозованої деталі. У загальному випадку проходження жорсткості деталі меншого розміру через нульове значення не збігається моментом проходження через це значення жорсткості прогнозованої деталі. У більшості випадків нульове значення жорсткості прогнозованої деталі і втрата її несучої здатності відбувається вже при від'ємних значеннях жорсткості деталі меншого розміру, тобто після плавного проходження нею нульового значення. Прогнозована деталь практично не змінює своєї жорсткості в момент проходження жорсткості деталі меншого розміру через нульове значення, але стрибкоподібне змінює жорсткість до нульового і від'ємного значень при досягненні деталі меншого розміру критичної від'ємної жорсткості, що залежить від розмірів прогнозованої деталі. Розрахунок жорсткості спрощується для простих симетричних тіл. Pпp = 7 G= r nG1 + CG2 , rn + C 39527 (1) де r - відстань від центра; n - коефіцієнт форми, має ціле значення для простих тіл і довільне для тіл довільної форми в діапазоні про 0 до 3, n=1 - для стрижня, 2 - для циліндра, 3 - для кулі, для тіл довільної форми визначається розрахунком або експериментально; E (n - 1)E G1 = , G2 = 1 - (n - 1)m (1+ m) m - коефіцієнт Пуассона; С - постійний по радіусі коефіцієнт, визначається за значенням жорсткості G0 на заданій відстані R0, що відповідає розмірові деталі меншого розміру. Якщо жорсткість деталі міняється в процесі деформування коефіцієнт С також міняється, але залишається однаковим для всіх значень r. Якщо залежність жорсткості деталі меншого розміру від переміщення u0 на відстані R0 представити у виді: G0=G 1+(G2–G 1)f(u0), (2) де залежності коефіцієнта С, жорсткості G, переміщень u, напруг s деталей довільного розміру r від переміщень u0 мають вигляд Rn f (u0 ) Rn (G2 - G1)f (u0 ) C= 0 , G = G1 + 0 , (3) 1 - f (u0 ) rn + (Rn - rn )f (u0 ) 0 æ n -1 ö u u0 ç R0 1 ÷ = +ç f (u )du0 , r R0 ç rn R0 ÷ò 0 ÷ è ø æ n -1 ö G1u0 ç G2R0 G ÷ +ç - 1 ÷ ò f (u0 )du0 R0 R0 ÷ ç rn è ø Формули (3) спрощуються при R0=1: æ 1 ö u = u0 + ç - 1÷ f (u )du ç n ÷ò 0 0 ; r èr ø æG ö s = G1u0 + ç 2 - G1÷ ò f (u0 )du0 ç r ÷ è n ø Для пластини з центральною тріщиною значення n можна оцінити розрахунковим шляхом за розрахованим значенням граничної жорсткості G2=-0,452E, що найбільше істотно впливає на несучу здатність деталі. Для цього використовуємо визначення G2 у розшифровці до формули (1). n=1-G2/E(1+m)=1-(-0,452Е)/Е(1+0,3)=1,5876. (4) s = Комп’ютерна в ерстка М. Ломалова 8 Використовуючи це значення n, виконаємо спрощений розрахунок несучої здатності пластини з центральною тріщиною, розміри й умови навантаження якої, а також експериментальні дані узяті з роботи [1]. Пластина шириною 2W=400мм із центральною тріщиною 2а=120мм руйнується при значенні коефіцієнта інтенсивності напружень K1с=81...84...84 МПа×м 0,5. Пластині шириною 200мм із такою же тріщиною відповідає K1с=61...67...67 МПа×м 0,5. Напруження визначимо по формулі [Кишкина С.И. Сопротивление разрушению алюминиевых сплавов. -М.:Металлургия,1981. - 279с.]: K1c 2W pa æ a ö , де f ç ÷ = tg . (5) æ a ö pa 2W èW ø paf ç ÷ èWø Для пластини шириною 2W=400мм - вони рівні s400=179,4... 186,1МПа, для 2W=200мм вони рівні s200=116,3... 127,7МПа. Функцію f(u0) у формулі (2) приймемо лінійної в найпростішому виді f(u0)=u0. Модуль пружності умовно приймемо рівним одиниці. Також приймемо, що пластині шириною 400мм відповідає розмір r=1, тоді пластині шириною 200мм буде відповідати розмір r=0,5. По формулі (3) для r=1 одержимо умовне значення максимуму відносних напруг 0,4423 при u0=0,73, для r=0,5 відповідно 0,28645 при u0=0,47. Таким чином, спрощений розрахунок жорсткості і несучої здатності пластини з центральною тріщиною, указує на збільшення несучої здатності пластини з тріщиною довжиною 2a=120мм при збільшенні її ширини з 2W=200мм до 2W=400мм. Це збільшення в 0,4423/0,28645=1,54 рази підтверджується експериментально s400 /s200=1,54... 1... 1,47. Для простих тіл при симетричній схемі навантаження розрахунок є точним, для реальних деталей спрощений розрахунок - наближеним у зв'язку з відмінністю схеми прикладання сил частини деталі з дефектом усередині прогнозованої деталі й в дослідній установці. Перевагою пропонованого способу в порівнянні з відомими розрахунковими способами визначення граничного стискаючого навантаження є те, що він припускає прямий вимір мінімальної жорсткості деталі з урахуванням не виявлених раніше дефектів, порушень технології, розкиду властивостей матеріалів, відхилень фактичних розмірів від розрахункових і інші факторів. Спосіб найбільш ефективний для деталей складної форми, для яких експериментальна перевірка більш актуальна. s= Підписне Тираж 28 прим. Міністерство осв іт и і науки України Держав ний департамент інтелектуальної в ласності, вул. Урицького, 45, м. Київ , МСП, 03680, Україна ДП “Український інститут промислов ої в ласності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determination of limit value of compression load on part
Автори англійськоюKarpinos Borys Serhiiovych, Barylo Viktor Hryhorovych
Назва патенту російськоюСпособ определения граничного значения нагрузки сжатия детали
Автори російськоюКарпинос Борис Сергеевич, Барило Виктор Григорьевич
МПК / Мітки
Мітки: деталі, визначення, значення, стискуючого, спосіб, навантаження, граничного
Код посилання
<a href="https://ua.patents.su/4-39527-sposib-viznachennya-granichnogo-znachennya-stiskuyuchogo-navantazhennya-detali.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення граничного значення стискуючого навантаження деталі</a>
Попередній патент: Спосіб формування біліодигестивного анастомозу
Наступний патент: Компресор
Випадковий патент: Датчик тиску або сили








