Спосіб формування частотно-модульованих сигналів з компактним спектром

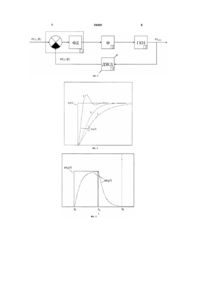
Спосіб формування частотно-модульованих сигналів з компактним спектром, що включає фа 3 39481 динамічного перехідного режиму, що виникає в системі фазової автопідстройки частоти на стрибкоподібну зміну значення коефіцієнта ділення дільника частоти у цепі зворотного зв’язку, при цьому системні параметри синтезатора частоти обирають такими, щоб перехідний процес мав аперіодичний характер. Зміст заявленого способу пояснюється наступним. На Фіг.1 приведена структурна схема пристрою СЧ непрямого типу, де: w1 и j1 - частота та фаза сигналу ЕГ СЧ (на Фіг.1 ЕГ умовно не показаний); w2 и j2 - частота та фаза приведеного до другого входу детектора 1 фазового (ФД) сигналу ГКН 3, що пройшов через ДЗКД 4, при цьому ГКН 3 керується за частотою напругою Uyпp, що отримується в результаті фільтрації фільтром 2 нижніх частот (Ф) сигналу з ви ходу ФД 1, пропорційного різниці фаз (j1-j2) сигналів на його входах. У зв’язку з тим, що система ФАПЧ як система регулювання за відхиленням, є астатичною за частотою, але статичною за фазою, усталений режим характеризується наступними співвідношеннями: w1 = w2, при t ® ¥, j1 ¹ j 2, тому що керуючий сигнал Uyпp на ГКН, що отримується на виході Ф пропорційний цій різниці фаз (j1 - j2). Якщо коефіцієнт ділення ДЗКД дорівнює N, то частота ви хідного сигналу ГКН wвих = w2 × N = w1 × N t ®¥ . Перехід СЧ від однієї частоти до іншої виконується шляхом стрибкоподібної зміни значення коефіцієнта ділення N ДЗКД. Незважаючи на те, що ФД - нелінійний пристрій, для фазових співвідношень - це віднімач, тобто лінійний пристрій. Цьому подібна зміна значення параметра N еквівалентно стрибкоподібній зміні частоти сигналу ЕГ. СЧ непрямого синтезу мають петлю негативного зворотного зв’язку (ЗЗ), що виробляє такий керуючий сигнал, щоб частота сигналу на виході СЧ була в N раз більше частоти сигналу ЕГ. Перехід від однієї частоти до іншої не здійснюється миттєво. Перехід СЧ до нової частоти (нового стану) супроводжується перехідними процесами та існує теоретично безкінечно довго [Андронов А.А., Витт А., Ха тин С.Э. "Теория колебаний". - М.: Наука, 1981 - 568 с.]. Практично же його обмежують певними умовами. Якщо у схемі СЧ непрямого типу прийняти, що Ф - це інтегруючий фільтр нижніх частот (ФНЧ) першого порядку, тоді весь СЧ буде являти собою систему друго го порядку, що описується лінійним неоднорідним диференційним рівнянням другого порядку вигляду: d2w2 (t ) dw (t ) + a1 × 2 + a 0 × w 2( t) = b × w1 , (1) dt 2 dt де: w1 - значення частоти сигналу ЕГ; а0, а1, b - коефіцієнти, що залежать від параметрів елементів системи. Рішення диференційного рівняння (1) описує закон зміни в часі частоти w2(t) сигналу на виході СЧ, що приведена до входу ФД. Характеристичне рівняння, відповідне даному диференційному, має 4 два кореня, тип та співвідношення яких буде визначати режим перехідного процесу. Характер зміни частоти сигналу ЕГ та частоти сигналу на виході СЧ у різних режимах роботи системи приведені на Фіг.2 (1 - аперіодичний, 2 - критичний, 3 квазіперіодичний). Якщо в системі виконані умови стійкості [Андронов А.А., Витт А., Хайкин С.Э. "Теория колебаний". - М.: Наука, 1981 - 568 с., Волощук Ю.І. "Сигнали та процеси у радіотехніці": Підручник для студентів ВНЗ: У 4-х т. - X.: ТОВ "Компанія СМІТ", 2005. - Т. 3: 528 с., с. 451 Баскаков С.И. "Радиотехнические цепи и сигналы": Учеб. Для ВУЗов по спец. "Радиотехника". - 2-е изд., перераб. и доп. - М.: Высш. шк., 1988 - 448 с.: ил., с. 200, 212], то в усі х трьох режимах частота w2 буде стремиться до частоти сигналу ЕГ w1 . Таким чином, у перехідному режимі сигнал на виході СЧ непрямого типу представляє собою радіосигнал з кутовою модуляцією (KM), закон зміни частоти якого описується функцією w2(t), а девіація частоти визначається величиною скачка частоти сигналу ЕГ w1 (або, що еквівалентно, величиною скачка параметра N). Визначимо спектральні характеристики такого радіосигналу. Для аперіодичного режиму перехідного процесу, що й визначає закон зміни в часі приросту частоти радіосигналу на виході СЧ справедливий вираз: Dw2 (t ) = C1 × ek 1×t + C2 × ek 2 ×t + Dw1 , t > 0, (2) де: Dw1 - приріст частоти сигналу ЕГ; С1,2 - константи, що залежать від початкових умов диференціального рівняння (1), що описує роботу системи; k1,2 - корни характеристичного рівняння, що відповідає диференційному рівнянню (1) системи. Якщо в якості керуючого сигналу розглядати імпульсний сигнал, що визначається значенням коефіцієнта ділення N, а система працює в аперіодичному режимі, тоді закон зміни приросту частоти ви хідного сигналу буде мати вигляд, що приведений на Фіг.3. Для отримання спектральної функції даного радіосигналу на виході СЧ його часове представлення було розділено на три частини: гармонічний сигнал до початку перехідного процесу, ланка сигналу під час перехідного процесу, гармонічний сигнал після закінчення перехідного процесу: ì s1( t) = Um × cos(w0 × ( t - t 0 )) t £ t0 ï s(t ) = ís 2( t) = Um × cos(w0 × ( t - t 0 ) + y(t )) t 0 tk m 0 k k î 3 де: t0 > 0- момент часу початку перехідного процесу; tk - момент часу закінчення перехідного процесу (t k > t0); Um - амплітуда радіосигналу; w0 - ви хідна частота радіосигналу до начала перехідного процесу; y(t) - зміна фази радіосигналу, відповідна зміні частоти, що визначається перехідним процесом (Фіг.3): 5 39481 6 t ò tk ò Dw2 ( x - t 0 ) × dx , t є [t 0, t k]; (4) qk = w0 × (t k - t0 ) + y(t ) = w0 × (t k - t 0 ) + Dw2 (x - t 0 ) × dx . (5) qk(t) - початкова фаза радіосигналу s 3(t), що визначається: В загальному вигляді спектральна функція радіосигналу (3) має вигляд: y( t) = t0 t0 t0 S(w) = òU tk m × cos(w0 × (t - t 0 )) × e - j× w× t ò × dt + Um × cos(w0 × ( t - t 0 ) + y(t )) × e- j ×w ×t × dt + -¥ t0 . (6) ¥ ò + Um × cos(w0 × ( t - t k ) + qk ) × e - j × w× t × dt = S1(w) + S2 (w) + S3 (w) tk Перша s 1(t) та третя s 3(t) ланки являють собою представлення визначається в аналітичному винапівнезкінчені гармонічні сигнали. їх спектральне гляді: ì ü U ï é 1 1 ùï - j×w×t0 S1(w) = m × íp × [d(w - w0 ) + d(w + w0 )] + j × ê + ; (7) úý × e 2 ï ë w - w0 w + w 0 ûï î þ S 3 (w) = ì ü é e j × qk Um ï e - j× qk ù ï - j× w × tk j× q - j ×q . (8) × íp × d(w - w0 ) × e k + d (w + w 0 ) × e k - j × ê + úý × e 2 ï w - w0 w + w0 û ï ë î þ [ ] Друга ланка s 2(t) представляє собою радіоімпульс с КМ, закон зміни приросту частоти якого визначається залежністю Dw2(t). Спектральна функція такого радіоімпульсу не виражається ні в елементарних, ні в спеціальних функціях. Тому вигляд спектральної функції другої ланки знаходимо численними методами за допомогою перетворення Фур’є. Для спрощення численних розрахунків перейдемо від розрахунку спектральної функції S2(w) до розрахунку спектральної функції комплексної обвідної радіоімпульсу s 2(t) [Волощук Ю.І. "Сигна ли та процеси в радіотехніці": Підручник для ВНЗ. Ч.1 Харків: ХНУРЭ, 2003. 648 с., с. 285, Баскаков С.И. "Радиотехнические цепи и сигналы": Учеб. Для ВУЗов по спец. "Радиотехника". - 2-е изд., перераб. и доп. - М.: Высш. шк, 1988 - 448 с: ил., с. 122]. Якщо в якості опорної частоти обрати вихідну частоту радіосигналу до початку перехідного процесу w 0, тоді спектральна функція комплексної обвідної буде мати вигляд: ìt x æ éC ùö C ï U(w) = Um × e - j×w0 ×t0 × í expç j × ê 11 × ek1×( t- t0 ) - 1 + 21 × e k 2×( t- t0 ) - 1 + Dw1 × ( t - t 0 ) - w × tú ÷ × dt + ç ÷ k1 k2 ûø ï t0 è ë î , (9) tk æ é C12 ùö ü C22 ï + exp ç j × ê × ek 1×( t -tx ) - 1 + × ek 2 ×( t -tx ) - 1 + D qx - w × t ú ÷ × dt ý ç ë k1 k2 û÷ ï è ø þ tx де: Модуль спектральної функції комплексної обСі,1 и Сі,2 - константи, що визначаються з почавідної (9) радіоімпульсу s 2(t) показаний на Фіг.4. ткових умов рівняння (1) для першої та другої часТоді спектральна функція другої ланки може тин перехідного процесу; бути представлена в вигляді: tx - момент часу закінчення першої частини 1 1 * S 2( w) = × U(w - w0 ) + × U (- w - w0 ) . (12) перехідного процесу такий, що: 2 2 t +t Спектральний аналіз другої ланки показав, що t x = 0 k ; (10) 2 відповідний йому частотно-модульований сигнал є сигналом с компактним спектром, тому що більша C11 C 21 k1 ×(t x -t 0 ) k 2 ×(t x -t 0 ) . (11) D qx = × (e - 1) + × (e - 1) + D w1 × ( t x - t0 ) частина його енергії зосереджена в обмеженій k1 k2 полосі, ширина якої приблизно дорівнює девіації Вираз (10) обґрунтовується симетричністю печастоти Dw 1. рехідних характеристик системи відносно моменту часу t x при формуванні першої та др угої частин перехідного процесу. ( ò ò ( ) ) ( ) ( ) 7 39481 8 9 Комп’ютерна в ерстка А. Крулевський 39481 Підписне 10 Тираж 28 прим. Міністерство осв іт и і науки України Держав ний департамент інтелектуальної в ласності, вул. Урицького, 45, м. Київ , МСП, 03680, Україна ДП “Український інститут промислов ої в ласності”, вул. Глазунова, 1, м. Київ – 42, 01601