Спосіб визначення фази за даними про амплітуду

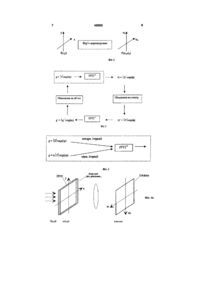
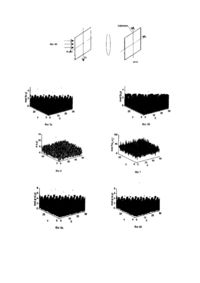
УКРАЇНА МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ДЕРЖАВНИЙ ДЕПАРТАМЕНТ ІНТЕЛЕКТУАЛЬНОЇ ВЛАСНОСТІ (із) U A ОПИС (11)48880 (із) А (51) 6 G02B27/22.G02B5/00 ДО ДЕКЛАРАЦІЙНОГО ПАТЕНТУ НА ВИНАХІД видається під відповідальність власника патенту (54) СПОСІБ ВИЗНАЧЕННЯ ФАЗИ ЗАДАНИМИ ПРО АМПЛІТУДУ (21)2002031757 (22) 04 03 2002 (24)15 08 2002 (46)15 08 2002, Бюл № 8, 2002 р (72) Кузьменко Олександр Васильович, Комаров В'ячеслав Олександрович, Єжов Павло Валентинович (73) МІЖНАРОДНИЙ ЦЕНТР "ІНСТИТУТ ПРИКЛАДНОЇ ОПТИКИ" НАЦІОНАЛЬНОЇ АКАДЕМІЇ НАУК УКРАЇНИ, Винахід відноситься до області фізики, зокрема, до оптичної голографи, а також до електронної техніки, і може бути використаний в електронній мікроскопи, рентгенівській кристалографи, оптичній астрономи, радіотехніці Винахід спрямований на рішення так званої "фазової проблеми", що виникає в зв'язку з тим, що по фізико-технічних причинах на практиці можливо вимірювати амплітуду чи інтенсивність дифрагованого поля, але не можливо вимірити його фазу В багатьох випадках дані про амплітуду випромінювання одержують, проводячи виміри в двох площинах - об'єктній і(чи) спектральній, зв'язаних між собою перетворенням Фур'є (фіг 1) Рішення "фазової проблеми" полягає в тому, щоб за відомими даними про модулі амплітуд функцій об'єкта |f(x,y)| і(чи) його спектра |F(cox,coy)| визначити ВІДПОВІДНІ їм фазові розподіли і, таким чином, відтворити повну картину поля в обох площинах, тобто комплекснозначні функції f(x,y) і F(cox,coy) В електронній мікроскопи, при конструюванні антен-випромінювачів із заданою формою сигналу в радіотехніці, кодуванні фаз і формуванні спектра в цифровій голографи, lf(x,y)l і IF(cox,coy)| ВІДОМІ (обміряні або задані а рпогу) як в об'єктній, так і спектральній площинах Фізично вони представлені ВІДПОВІДНО дифрактограмою, картиною електричного поля чи оптичним елементом транспарантного типу У цих випадках, вирішуючи задачу визначення фазових розподілів для функцій f(x,y) і F(cox,coy), говорять про задачу синтезу Фур'є-пари, що має задані властивості У рентгенівській кристалографи, Фур'єспектроскопп, оптичній астрономії вимірюють звичайно модуль амплітуди функції F(cox,coy), про функцію же об'єкта відомо лише те, що вона дійсна, невід'ємна і просторово обмежена У цих випадках фізичним носієм інформації є дифрактограма чи оптичне зображення, і, знаходячи ВІДПОВІДНІ фазові розподіли, говорять про задачу реконструкції об'єкта Обидві вказані задачі поєднуються в одну, загальну задачу в слідуючій постановці Задано дві системи обмежень (умов), одна з них накладається на об'єкт f(x,y), інша - на спектр цього об'єкта F(cox,coy) Необхідно знайти таку Фур'єпару об'єкт-спектр, що задовольняє обом системам обмежень (1) ВІДОМІ способи формування Фур'є-пари із заданими властивостями для цілей а) виготовлення оптимального, об'єктноорієнтованого дифузного розсіювача у Фур'єголографп (US Patent № 3 619 022, МКВ 6 G02B 5/00, 27/00, 1971 Hirsch Р М Jordan, J A Lezem L В Method of making an object-dependent diffuser), б) виготовлення оптичного елемента типу Фурье-кіноформа дифузного об'єкта з низьким рівнем шумів відтвореного зображення (Gallagher N С, Liu В Method for computing kmoform that reduces image reconstruction error Appl Opt 12, 2328 2335, 1973), в) рішення фазової проблеми в електронній мікроскопи (Gerchberg R W , Saxton W О A practical algorithm for the determination of phase from image and diffraction plane picture, Optik, 35, 237 - 246, 1972) У кожнім з цих трьох способів використовується один і той самий ітераційний алгоритм, відомий зараз як "error-reduction" алгоритм Відомий також спосіб формування Фур'є-пари по так званому "input-output" алгоритму (Fienup J R Phase retrieval algorithm a comparison О 00 00 00 48880 Appl Opt 21, 2758 - 2769, 1982), що відрізняється від "error-reduction" - способу формою представлення об'єктної функції На практиці вибір того чи іншого способу формування Фур'є-пари залежить від типу розв'язуваної задачі (синтезу чи реконструкції) та виду об'єкта і (чи) його спектра Критерієм того, що Фур'єпара сформована вірно, або, що те ж саме - вірно і точно визначені фазові розподіли у площинах об'єкт-спектр, при вирішенні задачі синтезу є якість відтвореного зображення об'єкта (наприклад, оптичного), а при вирішенні задачі реконструкції ступінь ВІДПОВІДНОСТІ початковим умовам (обмеженням) на об'єкт та(або) спектр КІЛЬКІСНО це визначається шляхом обчислення середньоквадратичного відхилення (дисперсії) модулів амплітуд сформованої Фур'є-пари від амплітуд в площинах об'єкт-спектр заданих в якості необхідних умов При роботі з об'єктами і (чи) спектрами досить складного виду, часто нульовий чи досить малий рівень дисперсії амплітуд у площинах об'єктспектр не досягається, що не задовольняє вимогам практики Як прототип обрано спосіб одержання об'єктно-орієнтованого дифузного розсіювача (US Patent № 3 619 022, МКВ 6 G02B 5/00, 27/00, 1971 Hirsch Р М Jordan, J A Lezem L В Method of making an object-dependent diffuser) шляхом формування Фур'є-пари з комплексних функцій f(x,y) = lf(x,y)l ехріф(х.у) (об'єкт) і F(cox,coy) = IF(cox,coy)l ехріф(а>х,а>у) (Фур'є-спектр) за рахунок повторного використання відносно f(x,y) і F(cox,coy) ВІДПОВІДНО прямого і зворотного перетворень Фур'є, врахуванні в цих даних про амплітуди |f(x,y)| і |F(cox,coy)l на кожному кроці ітерацій, при відповідному контролі збіжності ітераційного процесу Спосіб-прототип передбачає наступне 1 Функція f(x,y) описує хвильове поле у випромінюючій (об'єктній) площині X,Y і для неї а) при рішенні задач синтезу Фур'є-пари з даними властивостями, відомий (як результат вимірювань або заданий a priory) |fo(x,y)|, б) при вирішенні задач реконструкції об'єкта використовується та умова, що вона є дійсна, невід'ємна і просторово обмежена Початковий розподіл фаз сро(х,у) в а,б) випадках формується за допомогою генератора випадкових чисел в ЕОМ або з урахуванням характерних особливостей об'єкта 2 Функція F(cox,coy), отримана як результат прямого Фур'є-перетворення об'єктного поля f(x,y), описує хвильове поле в зоні дифракції і для неї відомий (як результат вимірювань або заданий а priory) |Fo(cox,coy)l 3 ВІДПОВІДНІСТЬ початковим умовам в процесі ітерацій для функції f(x,y) означає у випадку 1а заміну на кожному кроці ітерацій розподілу |f(x,y)|, отриманого прямим Фур'є-перетворенням, на |fo(x,y)| при збереженні незмінним розподілу ф(х,у), у випадку 16 - збереження в розподілі lf(x,y)l лише додатних значень у ВІДПОВІДНИХ просторових межах 4 ВІДПОВІДНІСТЬ початковим умовам в процесі ітерацій для функції F(cox,coy) означає заміну |F(cox,coy)|, отриманого прямим Фур'єперетворенням, на |Fo(cox,coy)| при збереженні не змінним ф((Ох,СОу) 5 Критерієм точності визначення фазових розподілів ф(х,у),ф(сох,Юу) є досягнутий мінімум середньоквадратичного відхилення (дисперсії) амплітуд |f(x,y)| (|F(cox,coy)|) від |fo(x,y)| (|Fo(cox,coy)|) у процесі ітерацій та його величина На фіг 2 приведена блок-схема алгоритму формування Фур'є-пари по способу-прототипу До недоліків прототипу можна віднести наступні При застосуванні його до об'єктів та(або) спектрів, що мають складний вигляд, достатньо часто не вдається досягти нульового або достатньо малого рівня дисперсії амплітуди в площинах об'єктспектр ВІДПОВІДНО НИЗЬКОЮ ВИЯВЛЯЄТЬСЯ також точність визначення фаз Ф, ф в цих площинах На практиці це призводить до невисокої якості фізикотехнічних елементів, які виготовляються на основі даного способу Задача пропонованого винаходу - підвищити точність визначення фазових розподілів Ф(х,у),ф(сох,соу) шляхом часткової зміни алгоритму формування Фур'є-пари (по середньоквадратичному критерію для амплітуд) і за рахунок цього підвищити якість фізико-технічних елементів (оптико-голографічних, кіноформних, для оптичної пам'яті і т ін), виготовлених або відтворених (наприклад, при опрацюванні оптичних зображень) на його основі Вирішення поставленої задачі досягається тим, що в способі визначення фази за даними про амплітуд}' вводиться нова операція обробки інформації в об'єктній площині, суть якої в тому, що в процесі ітерацій об'єктна функція f(x,y) спеціальним чином видозмінюється шляхом множення її на коефіцієнти Г im ' I glm І (2) Де 0 И т - ВИДОЗМІНЮЮЧІ КОефіЦІЄНТИ, |f°im| - початкові значення модуля амплітуди об'єкта, |діт| - значення об'єктної функції, одержувані в процесі ітерацій, 1,т = І , ,N,N N - множина дискретних ВІДЛІКІВ функцій f°(x,y), g(x,y), На блок-схемі фіг 2, блок, обведений штрихом, замінюється блоком, приведеним на фіг З Робота алгоритму зміниться тепер наступним чином Формування вхідної функції |fo(x,y)| ехріф(х.у) для FFT2 +1 і вся обробка, аж до одержання функції 9~(Х.У) ~ |д~(х,у)|ехр(іф(х,у)), на першій ітерації ЗДІЙСНЮЮТЬСЯ так, як і в способі-прототипі Далі розраховуються ВИДОЗМІНЮЮЧІ коефіцієнти о(х.у) = |fW)|/|g~(x>y)| (3) і формується функція g - а(х,у) І f(x,y) | ехрОч^у)), (4) +1 яка відтепер служить вхідною для FFT2 на другій ітерації При наступних ітераціях відбувається чергування - на непарних ітераціях алгоритм відпрацьовує звичайним чином, а на парних в нього включається операція ВІДОЗМІНИ об'єкту Винахід пояснюється ілюстраціями, на яких зображено Фіг 1 Площини, пов'язані перетворенням Фу 48880 рє Фіг 2 Блок-схема ітераційного процесу формування Фур'є-пари Фіг 3 Представлення об'єктної функції в процесі ітерації Фіг 4 Схеми а) синтезу кіноформа, б) відтворення зображення Фіг 5 Ідеальні об'єкти а) регулярна бінарна структура, б) статистична бінарна структура Фіг 6 Об'єктно-орієнтований фазовий розсіювач Фіг 7 Оптимізований амплітудний розподіл у площині кіноформа Фіг 8, 9 Відтворені зображення об'єктів, приведених на фіг 5, при синтезі киноформа а) запропонованим способом, б) за способомпрототипом Фіг 10 Залежність дисперсії амплітуд відтвореного зображення від номера ітерації а) для об'єкта фіг 5а, б) для об'єкта фіг 56 Фіг 11 Залежність розмаху амплітуди відтвореного зображення від номера ітерації а) для об'єкта фіг 5а, б) для об'єкта фіг 56 На фіг 1 0 - 1 1 криві 1 характеризують запропонований спосіб, криві 2 - спосіб-прототип Як показали фізичний аналіз та модельні експерименти на ЕОМ, виконані авторами, доповнення "error-reduction''-алгоритму вищеописаною операцією видозміни об'єкту дозволяє підвищити точність визначення фазових розподілів Ф(х,у),ф(сох,соу) у середньому в кілька разів за критерієм середньоквадратичного відхилення амплітуд Фур'є-пари Запропонований винахід пояснюється також наступним прикладом його реалізації ПРИКЛАД Моделювали в ЕОМ процес одержання Фур'є-кшоформа довільного плоского об'єкта при мінімізації шумів відтвореного зображення та пов'язаний з цим процес формування об'єктноорієнтованого дифузного розсіювача (фіг 4а,б) В постановці (1) задача формулюється таким чином Задані початкові умови - значення функцій |fo(x,y)| об'єкта та |Fo(cox,coy)| - спектра цього об'єкту, причому необхідно, щоб |F(cox,cov)| и const по всій спектральній площині (основна умова кіноформної реєстрації) Потрібно синтезувати Фур'єпару f = |f(x,y)| ехр(іф(х,у)), F = |F(cox,coy)| ехр(іф(сох,Юу)), яка відповідає поставленим умовам На мові фізики це означає -необхідно віднайти такий фазовий розподіл ср(х,у) (дифузний фазовий розсіювач), який забезпечить максимально рівномірний розподіл енергії світла (|F|2 « const) у площині реєстрації кіноформу При цьому запис кіноформу (фазового розподілу ф(сох,соу)) на фізичному середовищі (при умові |F(cox,coy)| = const), відбувається з мінімальними втратами інформації, що, в свою чергу, мінімізує шуми відтвореного зображення об'єкту (функції д(х,у)) На фіг 5 - 11 - результати машинного моделювання по формуванню і реєстрації Фур'єкіноформів за допомогою запропонованого способу і способу-прототипу, зображення відтворених об'єктів, графіки для порівняльного аналізу, які демонструють переваги запропонованого способу перед прототипом Основним показником якості відтвореного зображення є дисперсія сг|д| його амплітуди, розрахована по формулі (Г Корн, Т Корн Справочник по математике, "Наука", Москва, 1974) > iml (5) Д оЄ |f 1m|, об'єк|gim| " ЗНаЧЄННЯ ЭМПЛГГуД та(початкові) і відтвореного зображення, А = Z |9іт 1 m - сума всіх амплітуд зображення, 1,т = 1, ,N,N N - множина всіх дискретних значень амплітуди об'єкта (зображення) у площині х,У Значення сг|д| характеризують ступінь відхилення амплітуд відтвореного зображення від ідеальних амплітуд (заданих в якості початкових умов) На фіг 10 видно, що запропонований спосіб дає змогу досягти значно менших рівнів сг|д| у порівнянні зі способом-прототипом В наших експериментах з декількома десятками різних бінарних об'єктів зменшення сг|д| складало від двох до десяти і більше разів На фіг 11 - залежність розмаху Agmax амплітуди від ітерації, розрахована по формулі Agmax = (1/А) (|g|max - |g|min)> (6) яка характеризує максимальне локальне відхилення сформованої амплітуди від заданої Видно, що спосіб суттєво покращує також і цей параметр Зменшення дисперсії і розмаху можна спостерігати візуально, порівнюючи зображення на фіг 8, 9 з ідеальними об'єктами (фіг 5) Слід відзначиш, що, як видно з графіків на фіг 10, 11, в приведеному прикладі використання операції ВІДОЗМІНИ об'єкту на всіх парних ітераціях процесу формування Фур'є-пари не є обов'язковим Оскільки дисперсія і розмах у процесі ітерацій зменшуються монотонно, достатньо одноразово виконати операцію ВІДОЗМІНИ об'єкту, досягнувши мінімуму сг|д| (Agmax) на "error-reduction" ітерації При цьому за один прохід отримуються мінімально можливі для запропонованого способу значення цих параметрів 48880 Фур'є-перетворювач Фіг.І If|ехр(іф> FFTT * | G | ехр(іф) Обмеження ка спектр Обмеження на об'єкт ' | ехр(і