Пристрій для телекерування об’єктами з дисперсійно-частотним компандуванням фінітних низькочастотних сигналів

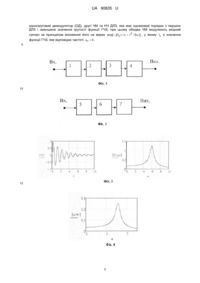
Реферат: Пристрій для телекерування об'єктами з дисперсійно-частотним компандуванням фінітних низькочастотних сигналів на передавальній стороні містить дисперсійну лінію затримки (ДЛЗ) певного порядку, функція групового часу затримки (ГЧЗ) якої має певне значення крутості а. ДЛЗ є низкочастотною (НЧ) лінією, на вході якої уведено частотний модулятор (ЧМ), на її виході - фільтр нижніх частот (ФНЧ), на виході якого введено односмуговий модулятор (ОМ). На приймальній стороні пристрою введено послідовно з'єднані односмуговий демодулятор (ОД), другі ЧМ та НЧ ДЛЗ, яка має однаковий порядок з першою ДЛЗ і зменшене значення крутості функції ГЧЗ. Обидва ЧМ модулюють вхідний сигнал за принципом множення його на вираз exp[  j( t н  /    2 / 2 )] , у якому t н є значення функції ГЧЗ, яке відповідає частоті н  0 . UA 90835 U (12) UA 90835 U UA 90835 U 5 10 15 Корисна модель належить до вимірювальної техніки і призначена для замкнутого автоматичного телекерування фізичним об'єктом з досягненням скорочення часу відхилення його від нормальної безперервної роботи. Крім аналізу спектра сигналів [Тверской В.И. Дисперсионно-временные методы измерения спектров радиосигналов. - М: "Советское радио", 1974] відомі також можливості використання смугової дисперсійної лінії затримки (ДЛЗ) і для частотного компандування високочастотних (ВЧ) радіосигналів у межах робочої області частот групового часу затримки (ГЧЗ) лінії [Зверев В.А. К вопросу о сжатии и расплывании модулированных сигналов в диспергирующих средах. « Известия ВУЗов. Радиофизика", № 1, 1970]. При цьому принципи частотної компресії функцій часу основані на відомої властивості прямого перетворення Фур'є зміни масштабу. У відомих аналогах, через складності аналітичного виразу коефіцієнта зміни масштабу, складною одержується реалізація їх з використанням двох ДЛЗ в окремому пристрою. Найбільш близьким аналогом до технічного рішення, що заявляється, є лише принцип дисперсійно-частотної компресії зі спрощеним виразом коефіцієнта зміни масштабу окремою смуговою ДЛЗ [Клаудер И.К., Прайс А.С и др. Теория и расчёт импульсных РЛС. "Зарубежная радиоэлектроника" № 1, 1961]. Згідно з цім принципом відгуком смугової ДЛЗ, яка має передаточну функцію виду: K( j)  exp j (  0 ) U1( t )  u1( t ) exp j(0 t  kt 2 ) 20 30 35 40 також , на комплексну ВЧ напругу впливу  4k комплексна ВЧ напруга виду: k u1( 2kt ) є обвідною U2 ( t )  k u1( 2kt ) exp j(0 t  kt 2   . Цe означає, що вираз  4  комплексної ВЧ напруги U2 (t ) і вона має коефіцієнт зміни масштабу 2k та коефіцієнт зміни рівня 25 є 2 k .  В основу корисної моделі поставлена задача одержання реальної системи телекерування об'єктами з дисперсійно-частотним компандуванням фінітних низькочастотних (НЧ) сигналів. Поставлена задача вирішується тим, що пристрій, що містить на передавальній стороні, дисперсійну лінію затримки (ДЛЗ) певного порядку, функція групового часу затримки (ГЧЗ) якої має певне значення крутості, а, згідно з корисною моделлю, ДЛЗ є низкочастотною (НЧ) лінією, на вході якої введено частотний модулятор (ЧМ), а на її виході - фільтр нижніх частот (ФНЧ), на виході якого введено односмуговий модулятор (ОМ), і на приймальній стороні пристрою введено послідовно з'єднані односмуговий демодулятор (ОД), другі ЧМ та НЧ ДЛЗ, яка має однаковий порядок з першою ДЛЗ і зменшене значення крутості функції ГЧЗ, при цьому обидва ЧМ модулюють вхідній сигнал за принципом множення його на вираз exp[  j( t н  /    2 / 2 )] , у якому tн є значення функції ГЧЗ, яке відповідає частоті н  0 . Корисна модель пояснюється кресленнями, де на фіг. 1, наведена структурна електрична схема передавальної частині пристрою, який містить послідовно з'єднані частотний модулятор (ЧМ) 1, НЧ ДЛЗ 2, які представляють частотний компресор, фільтр нижніх частот (ФНЧ) 3 та односмуговий модулятор (ОМ) 4, а на приймальної стороні фіг. 2 пристрій містить послідовно з'єднані односмуговий демодулятор (ОД) 5, ЧМ 6 та ДЛЗ 7 - частотний експандер. Корисна модель працює наступним чином: Нехай напруга u1 сигналу, який потрібно аналізувати, надходить на вхід передавальної частини пристрою, у який входять послідовно з'єднані ЧМ 1, ДЛЗ 2, ФНЧ 3 - частотний 2   є відгуком exp j ( t  t н ) 2  2i   частотного компресора, де tн - значення функції ГЧЗ лінії, що відповідає частоті н  0 , бо вона є НЧ лінією, а параметр   t /  - крутість характеристики ГЧЗ лінії ДЛЗ 2. У цієї T  2   t   exp j t н  d формулі правий множник комплексна S(t / )   u1() exp j  exp j    2        0   спектральна функція, у якій лише перші два додатки представляють пряме перетворення Фур'є, а щоб його одержати необхідно напругу u1 умножити на останні дві експоненти з протилежним знаком. Обидві з цих експонент вказують на те, що вхідний сигнал блоками ЧМ 1 фіг. 1 та ЧМ 6 фіг. 2 необхідно виконати частотну модуляцію з протилежним знаком за формулою компресор та ОМ 4. Можна показати, що напруга u 2  Re 45 1 exp[  j( t н  /    2 / 2 )] . При цьому на виході ДЛЗ 2 фіг. 1 одержується така функція напруги u 2 , 1 UA 90835 U обвідна якої є функцією S( t /  )  5  1T  t   u1( ) exp j   d прямого перетворення Фур'є з 2  0   частотою t /  . Із порівняння цього виразу з відомим виразом властивості Фур'є f (kt )  1 F( ) k k зміни масштабу виходить, що коефіцієнт зміни масштабу k дорівнює крутості  функції ГЧЗ лінії. Отже, в залежності від значення цієї крутості можна одержувати як розширення (експандування), так і стискання (компресію) спектра при відповідній зміні його рівня за формулою  / 2 . Для підтвердження цього принципу із приведених графіків, одержаних у Maеhcad наглядно видно відмічені особливості перетворення Фур'є на прикладі НЧ ДЛЗ п'ятнадцятого порядку і функції діяння яка має комплексну спектральну функцію f (t )  exp( dt ) sin( t ) , 10 15 20 25 30 35 40 45 50 F()  2 . (b  j) 2   2 Так з графіків фіг. 3 видно, що функція f (t ) і модуль комплексної спектральної функції F() є практично фінітною функцією на інтервалі T  10m при коефіцієнті масштабування m  1, де число 10 представляє нормований інтервал частот таблиці [Туник В.Ф. Пристрій табульованих секцій дисперсійних ліній затримки нижчих частот на фазових контурах. Патент на корисну модель №72061 від 10.08.2012, Бюл. № 15]. Розгортка по горизонтальній осі графіків фіг 4 та фіг. 5 вибрана такою, при якій зовнішньо ці графіки приблизно подібні графіку функції F() фіг. 3. Порівняння чисельних відміток на горизонтальній осі графіка функції F() фіг. 3 і графіків фіг. 4 та фіг. 5 вказує на відповідний результат частотного компандування, що дозволяє виміряти значення цього результату. Так, наприклад, при коефіцієнті масштабування m  0.5 із графіка фіг. 4 видно, що одержується компресія частотного діапазону приблизно від 0 до 2.5 рад/с, тобто приблизно в 4 рази. І це є наслідком того, що крутизна  функції ГВЗ має значення 3.831, що значно більше, чим   0.958 при m  1. При коефіцієнті масштабування m  1.5 на виході ДЛЗ 7 фіг. 2, згідно з Фіг. 3 одержується частотний діапазон від 0 до 26 рад/с при значно зі зменшеної крутизною   0,426 , чим при коефіцієнті m  1. Аналогічно можна виміряти частотну смугу викиду спектральної функції фіг. 4 та фіг. 5 і зміну амплітуди цього викиду. Таким чином, дійсно на виході окремої ДЛЗ можна одержати необхідне значення частотної компресії фінітних ПЧ функцій при коефіцієнті масштабування m  1 і частотного експандування при m  1. З виходу ДЛЗ 2 фіг. 1 одержаний компресійний сигнал надходить на вхід фільтра ФПЧ 3, з його виходу сигнал надходить на вхід односмугового модулятора ОМ 4 фіг. 1, з виходу якого сигнал передається по певному каналу зв'язку згідно з його амплітудно-частотною характеристикою. Прийнятий сигнал надходить на вхід односмугового демодулятора ОД 5 фіг. 2, на виході якого одержується встановлений компресійний сигнал, який надходить на вхід частотного експандера з послідовно з'єднаними ЧМ 6 та ДЛЗ 7, на виході якої одержується встановлення сигналу напругою u1 . Таким чином, можна стверджувати, що запропонований пристрій дійсно у принципі і реально дозволяє вирішувати проблемну задачу телекерування фізичними об'єктами з дисперсійночастотним компандуванням фінітних НЧ сигналів при підвищенні перешкодостійкості їх, що саме і визначає практичну корисність упровадження його у науку і техніку. ФОРМУЛА КОРИСНОЇ МОДЕЛІ Пристрій для телекерування об'єктами з дисперсійно-частотним компандуванням фінітних низькочастотних сигналів, що на передавальній стороні містить дисперсійну лінію затримки (ДЛЗ) певного порядку, функція групового часу затримки (ГЧЗ) якої має певне значення крутості а, який відрізняється тим, що ця ДЛЗ є низкочастотною (НЧ) лінією, на вході якої введено частотний модулятор (ЧМ), на її виході - фільтр нижніх частот (ФНЧ), на виході якого введено односмуговий модулятор (ОМ), на приймальній стороні пристрою введено послідовно з'єднані 2 UA 90835 U односмуговий демодулятор (ОД), другі ЧМ та НЧ ДЛЗ, яка має однаковий порядок з першою ДЛЗ і зменшене значення крутості функції ГЧЗ, при цьому обидва ЧМ модулюють вхідний сигнал за принципом множення його на вираз exp[  j( t н  /    2 / 2 )] , у якому tн є значення функції ГЧЗ, яке відповідає частоті н  0 . 5 10 15 3 UA 90835 U Комп’ютерна верстка М. Ломалова Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4