Спосіб рішення задачі цілочисельного лінійного програмування з булевими змінними на основі рангового підходу та принципу оптимізації за напрямком

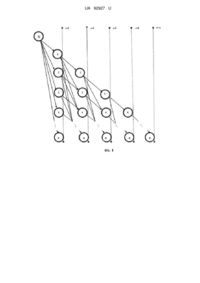
Реферат: Спосіб рішення задачі цілочисельного лінійного програмування з булевими змінними на основі рангового підходу та принципу оптимізації за напрямком, який вирішує задачу цілочисельного лінійного програмування з булевими змінними на основі рангового підходу та принципу оптимізації за напрямком. Введено правило відсікання неперспективних варіантів рішень по вибору максимального значення довжини шляху в графі за вагою функціоналу та сортування даних по зростанню значень коефіцієнтів в обмеженні. UA 92927 U (12) UA 92927 U UA 92927 U 5 Запропонована корисна модель належить до галузі кібернетики і обчислювальної техніки та може бути використана при вирішенні задач комбінаторної оптимізації на графах. Відомий "Спосіб послідовного призначення одиниць для наближеного рішення задачі про одномірний ранець", який вирішує задачу цілочисельного лінійного програмування з булевими змінними [1]:  f (x)  n  c j x j  max j 1 , (1) при виконанні умов: n  ijx j  b1 j 1 , (2)   , (3) x j  {0,1}, i  1 j  1 n , , 1j  0, 10 c j  0. , (4) В даному способі як початковий розглядається нульовий вектор, в якому змінним присвоюються одиничні значення за умови, що при побудові допустимого цілочисельного рішення z 0 призначаються одиничні значення у відповідності з послідовністю  j   j  ... j , 1 починаючи з найбільшого значення. Якщо для деякого z0 jk  jk 2 n таке призначення виконати 0 15 неможливо, тоді і переходять до номеру jk 1 . Процес завершується після перегляду усіх змінних, або при порушенні умови (2). Призначення одиничних значень виконується у 20 відповідності з послідовністю c j  c j  ...c j . Недоліком відомого способу є те, що відносна похибка наближеного алгоритму для рішення задачі цілочисельного лінійного програмування з булевими змінними складає 20 %. Найбільш близьким до запропонованого технічного рішення, вибраним як прототип, є "Способ решения задачи целочисленного линейного программирования с булевыми переменными на основе рангового похода", який вирішує задачу цілочисельного лінійного програмування з булевими змінними на основі рангового підходу, та полягає у тому, що з 1 2 n r 1 вершини s графа D будується множина шляхів msj , j  (1, n) першого рангу r , що задовольняє 25 властивості, і в множинах m r 1 sj * r     sj    визначаються шляхи максимальної довжини   за вагою функціонала c j [2]. Для кожної вершини j визначається вага  j за правилом:  j  c j 1  c j  2  ...  c n ,  n  0, j  (1 n  1) , Виключаються шляхи задовольняють нерівності:  , p  (r,n) r sp . (5) r r у множині m sj поточного рангу r , довжини якої dc ( sp )   * r    dc (r )   p  maxdc   sp  sp       {c j } 30 , (6) де  p  c p 1  c p  2  ...  c n та для вершини j  n вага  j - дорівнює нулю;   - довжина шляху від вершини s до вершини p dc  r sp Формується множина шляхів m r  r 1 sp , рангу r по вагах функціоналу. p  (1 n) наступного рангу, що задовольняє властивості , r (5), на базі множини шляхів m sj попереднього рангу на основі рекурентного співвідношення: r r 1  max {r U( j, p)} p  r  1 n j  r, n j  p , sp sj 35 {c j } , (7)  r U( j, p ) sj де - шлях з вершини s графа D у вершину p , що проходить через проміжну вершину j і задовольняє правилам, тобто який одержується за рахунок приєднання до шляху 1 UA 92927 U r sj ребра ( j, p) , якщо таке з'єднання не суперечить правилу відсікання неперспективних варіантів рішень. m r  r 1 sp 5 10 15 20 25 30 35 * r  r 1     sp    . Якщо визначиться  виділяються щонайменші шляхи  У визначених множинах декілька шляхів максимальної довжини, то серед них вибирається шлях з меншим значенням довжини за вагою обмежень aij. Перевіряється, чи вся множина шляхів наступного (r  1) -го рангу порожня. Якщо умова виконується, то в множинах виділяється шлях максимальної довжини і алгоритм закінчує роботу. Якщо умова не виконується, то перевіряється r  (n  1) . У разі виконання рівності в множині виділяється шлях максимальної довжини і алгоритм закінчує роботу, інакше збільшується г на 1 і виконується обчислення у відповідності до формул (5-7). Недоліком способу-прототипу є те, що відносна похибка наближеного алгоритму для рішення задачі цілочисельного лінійного програмування з булевими змінними на основі рангового підходу складає 12 %. В основу корисної моделі поставлена задача створити "Спосіб рішення задачі цілочисельного лінійного програмування з булевими змінними на основі рангового підходу та принципу оптимізації за напрямком", який дозволить зменшити відносну похибку алгоритму до 10 %. Поставлена задача вирішується за рахунок того, що успосіб-прототип, додатково введено правило відсікання неперспективних варіантів рішень на основі вибору максимального значення довжини шляху в графі за вагою функціоналу на основі принципу оптимізації за напрямком та сортування даних по зростанню значень коефіцієнтів в обмеженні. Технічний результат, який може бути отриманий при здійсненні корисної моделі, полягає у зменшенні відносної похибки алгоритму рішення задачі цілочисельного лінійного програмування з булевими змінними на основі рангового підходу та принципу оптимізації за напрямком до 10 %. На фіг. 1 представлено граф D . На фіг. 2 наведено приклад рішення задачі цілочисельного лінійного програмування з булевими змінними на основі рангового підходу та принципу оптимізації за напрямком. Запропонований "Спосіб рішення задачі цілочисельного лінійного програмування з булевими змінними на основі рангового підходу та принципу оптимізації за напрямком" ґрунтується на правилі відсікання неперспективних варіантів рішень по вибору максимального значення довжини шляху в графі за вагою функціоналу на основі принципу оптимізації за напрямком та сортуванні даних по зростанню значень коефіцієнтів в обмеженні. Суть способу полягає у наступному. Виконується сортування даних по зростанню значень коефіцієнтів в обмеженні: 1  2  3  ...  n . (8) r 1 З вершини s графа D будується множина шляхів m sj , j  (1, n) першого рангу r , що   * r   sj    задовольняє властивості, і в множинах визначаються шляхи максимальної довжини   за вагою функціонала c j . Для кожної вершини j визначається вага  j за правилом (5). m r 1 sj 40 r r r Виключаються шляхи { sp } , p  (r, n) у множині m sj поточного рангу r , довжини якої dc ( sp ) задовольняють нерівності (6). r  r 1 p  (1 n) наступного рангу, що задовольняє властивості , Формується множина шляхів m sp r 45 (5), на базі множини шляхів m sj попереднього рангу на основі правила відсікання неперспективних варіантів рішень по вибору максимального значення довжини шляху в графі за вагою функціоналу на основі принципу оптимізації за напрямком (7). m r  r 1 sp   * r  r 1   sp   .  виділяються щонайдовші шляхи  У визначених множинах Якщо визначиться декілька шляхів максимальної довжини, то серед них вибирається шлях з меншим значенням довжини за вагою обмежень a1j . 2 UA 92927 U 5 10 Перевіряється, чи вся множина шляхів наступного (r  1) -го рангу порожня. Якщо умова виконується, то в множинах виділяється шлях максимальної довжини і алгоритм закінчує роботу. Якщо умова не виконується, то перевіряється r  (n  1) . У разі виконання рівності в множині виділяється шлях максимальної довжини і алгоритм закінчує роботу, інакше збільшується r на 1 і виконується обчислення у відповідності до формул (5-7). Джерела інформації: 1. Сигал И.Х., Иванова А.П. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы: Учеб. пособие. - Изд. 2-е, испр. - М.: ФИЗМАТЛИТ, 2003. - 240 с. 2. Третьяк В.Ф., Голубничий Д.Ю.,Огурцов В.В. Метод решения задачи целочисленного линейного программирования с булевыми переменными на основе рангового похода // Системи обробки інформації. Збірник наукових праць, 2009. - випуск 4 (78). - С 152-155 15 ФОРМУЛА КОРИСНОЇ МОДЕЛІ 20 Спосіб рішення задачі цілочисельного лінійного програмування з булевими змінними на основі рангового підходу та принципу оптимізації за напрямком, який вирішує задачу цілочисельного лінійного програмування з булевими змінними на основі рангового підходу та принципу оптимізації за напрямком, який відрізняється тим, що введено правило відсікання неперспективних варіантів рішень по вибору максимального значення довжини шляху в графі за вагою функціоналу та сортування даних по зростанню значень коефіцієнтів в обмеженні. 3 UA 92927 U Комп’ютерна верстка І. Скворцова Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4