Сферична поверхня

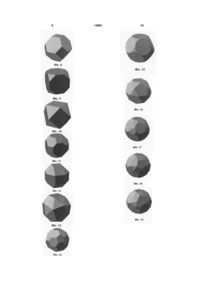
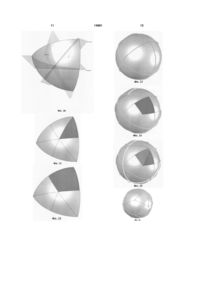
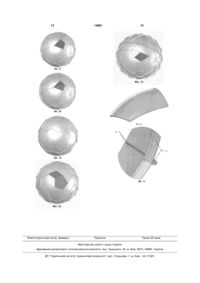
1. Сферична поверхня, зокрема сферичний проекційний екран для панорамного зображення за допомогою проекторів, виконана у вигляді зрізаної у межах кута огляду повної сфери, яка відрізняється тим, що вона складена впритул з окремих сферичних елементів у вигляді сегментів сфери, описаної навколо правильного або напівправильного багатогранника, зрізаних його гранями, довжина а ребер яких визначена із співвідношення: a = kR, де k - коефіцієнт пропорційності; R - радіус сфери. 2. Сферична поверхня за п. 1, яка відрізняється тим, що багатогранником є тетраедр з ребром трикутної грані, що дорівнює: 2 3 58 18 5 R. 109 15. Сферична поверхня за п. 1, яка відрізняється тим, що багатогранником є зрізаний додекаедр з ребром грані, що дорівнює: a 74 30 5 R. 61 16. Сферична поверхня за п. 1, яка відрізняється тим, що багатогранником є ікосододекаедр з ребром грані, що дорівнює: a 1 R. 2 17. Сферична поверхня за п. 1, яка відрізняється тим, що багатогранником є ромбозрізаний ікосододекаедр з ребром грані, що дорівнює: a a 5 2 31 12 5 R. 241 Корисна модель відноситься до криволінійних конструкцій різного призначення, зокрема, до сферичних поверхонь сферичного проекційного екрана для панорамного зображення за допомогою проекторів. Відомий будівельний каркас сферичної форми, у якому основні структурні елементи взаємопов'язані в геодезичну модель з утворенням сферичної сітки, вкритої шаром пластикового матеріалу [див. пат. US №2682235, 29.06.1954]. Відома також система сферичної проекції, яка містить сферичний проекційний екран у вигляді зрізаного сферичного сегменту [див. пат. US №4656506, Н04К9/31, 27.06.1986]. Недоліком відомих сферичних поверхонь є їх низька технологічність, пов'язана з відносно складними операціями їх виготовлення. Найбільш близьким до корисної моделі за технічною суттю і результатом, якого досягають, є сферичний проекційний екран для автомобільного тренажера [див. пат. US №4631867, В24В5/00, 19.02.1985], який утворений суцільним шаром синтетичного матеріалу і забезпечує відсутність швів. Одна форма виконання структури має суцільний шар синтетичного матеріалу, наклеєного на куполоподібну геодезичну структуру для досягнення достатньої міцності. Інша форма виконання має досить товстий шар синтетичного матеріалу з можливим армуванням. Спосіб виготовлення такого купола містить спорудження звичайної геодезичної структури і застосування обшивки синтетичним матеріалом внутрішньої поверхні структури. При цьому застосовується стелаж для інструментів, який забезпечує розміщення вісі повороту, від якої обертається інструментальна штанга для досягнення внутрішньої гладкої, суцільної і безшовної поверхні. 14881 4 18. Поверхня за п. 1, яка відрізняється тим, що багатогранником є ромбоікосододекаедр з ребром грані, що дорівнює: a 2 11 4 5 R. 41 19. Сферична поверхня за п. 1, яка відрізняється тим, що багатогранником є плосконосий додекаедр з ребром грані, що дорівнює: а = 0,46386R. 20. Сферична поверхня за будь-яким із пунктів 119, яка відрізняється тим, що вона складена впритул з частин сферичних сегментів, отриманих їх зрізанням площинами, які проведені через центр сфери і вершини багатогранника. 21. Сферична поверхня за будь-яким із пунктів 120, яка відрізняється тим, що сферичні сегменти виконані з холодноформованого склопластику. 22. Сферична поверхня за будь-яким із пунктів 121, яка відрізняється тим, що сферичні сегменти з одного боку мають ребра жорсткості вздовж їх сторін, а з протилежного боку мають вздовж їх сторін фаски. Недоліком прототипу є велика складність виготовлення сферичної поверхні і її вартість, недостатня якість отриманої поверхні, зокрема її неоднорідність, а також недостатня жорсткість в умовах вібрації, зокрема ускладнене виготовлення сферичного проекційного екрана для панорамного зображення за допомогою проекторів з потрібним кутом огляду. В основу корисної моделі поставлена задача спрощення виготовлення сферичної поверхні, зокрема сферичного проекційного екрана з потрібним кутом огляду, поліпшення якості його поверхні, підвищення механічної міцності і зменшення вартості. Технічний результат, якого досягають при використанні корисної моделі, полягає у тому, що сферична поверхня може бути отримана складанням з окремих сферичних сегментів у вигляді варіативних сферичних многокутників і їх частин. Зазначений технічний результат досягається тим, що сферична поверхня, зокрема сферичний проекційний екран для панорамного зображення за допомогою проекторів, виконана у вигляді зрізаної у межах кута огляду повної сфери і складена впритул з окремих сферичних елементів у вигляді сегментів сфери , описаної навколо правильного або напівправильного багатогранника, зрізаних його гранями, довжина а ребер яких визначена із співвідношення: a=kR, де: k - коефіцієнт пропорційності; R - радіус сфери. При цьому багатогранником може бути будьякий з можливих п'яти правильних багатогранників з відповідним значенням коефіцієнтах: 5 2 6 , 3 для тетраедра k 2 для куба k 14881 , 3 для октаедра k 2, для ікосаендра k для додекаедра k 10 2 5 , 5 5 1 . 3 Якщо багатогранником є будь-який з тринадцяти можливих напівправильнмх багатогранників, 2 22 , 11 то: для зрізаного тетраедра k 10 , 5 для зрізаного октаедра k для зрізаного куба k 2 7 4 2 17 для кубооктаедра k=1, для ромбозрізаного k 2 13 6 2 97 , кубооктаедра , для ромбокубоктаедра k 2 5 2 2 17 для плосконосого куба k=0,74421, 58 18 5 , 109 для зрізаного iкосаендра k для зрізаного додекаедра k для ікосододекаедра k для k ромбозрізаного 2 31 12 5 74 30 5 , 61 5 1 , 2 ікосододекаедра , 241 для ромооїкосододекаедра k льні багатогранники, у тому числі на Фіг.7 - зрізаний тетраедр, на Фіг.8 - зрізаний октаедр, на Фіг.9 зрізаний куб, на Фіг.10 - кубооктаедр, на Фіг.11 ромбозрізаний кубооктаедр, на Фіг.12 - ромбокубоктаедр, на Фіг.13 - плосконосий куб, на Фіг.14 зрізаний ікосаедр, на Фіг.15 - зрізаний додекаедр, на Фіг.16 -ікосододекаедр, на Фіг.17 - ромбозрізаний ікосододекаедр, на Фіг.18 - ромбоікосододекаедр, на Фіг.19 - плосконосий додекаедр; на Фіг.2022 - частини сферичних многокутників; на Фіг.23-25 - сферичні поверхні, отримані з варіантом багатогранника - октаедр; на Фіг.26-28 - сферичні поверхні, отримані з варіантом багатогранника - ікосаедр; на Фіг.29-31 - сферичні поверхні, отримані з варіантом багатогранника - зрізаний ікосаедр; на Фіг.32, 33 - чотирикутний сферичний сегмент. Сферична поверхня у вигляді сферичного проекційного екрану для панорамного зображення за допомогою проекторів (Фіг.1) виконана у вигляді зрізаної у межах кута огляду повної сфери і складена впритул з окремих сферичних елементів 1, 2 у вигляді сегментів сфери, описаної навколо правильного або напівправильного багатогранника (зрізаного ікосаедра), зрізаних його гранями (п'ятиі шестикутниками), довжина а ребер 3 яких визначена з співвідношення: а=kR, де: к - коефіцієнт пропорційності (для зрізаного 10 2 5 ), 5 R - радіус сфери. Сферична поверхня може бути складена з частин сферичних елементів, отриманих їх зрізанням площинами, які проведені через центр сфери і вершини багатогранника (на Фіг.20-22 - сферичні трикутники). При цьому сферичні сегменти можуть бути виконані з холодноформованого склопластика. Сферичні сегменти (Фіг.32, 33) з одного боку мають ребра жорсткості 4 вздовж їх сторін, а з протилежного боку мають вздовж їх сторін фаски 5. Розміри і кривизну сферичного сегмента визначають у відповідності з виразом: a=kR і технологічними можливостями виготовлювача. Сферичні сегменти потрібного розміру і кривизни отримують, наприклад шляхом лиття у форми або видавлюванням пуансонами у матрицях. Сферичну поверхню отримують складанням сферичних сегментів впритул їх ребрами з механічним або іншим кріпленням з одного боку і шпатлюванням швів між фасками 5 з протилежного боку. Для сферичних проекційних екранів їх робочу поверхню вкривають світловідбивальним матеріалом. Перевагою корисної моделі є можливість отримання сферичної поверхні, у тому числі зрізаної з потрібним кутом огляду, з мінімальної кількості геометричних варіантів сферичних сегментів. Так вона може бути складена з сферичних сегментів тільки одного типу, якщо багатогранник є правильним (Фіг.2-6), або - з декількох типів, якщо багатогранник напівправильний (Фіг.7-19). ікосаендра k , 2 11 4 5 , 41 для плосконосого додекаедра k=0,46386. Сферична поверхня може бути складена впритул і з частин сферичних сегментів, отриманих їх зрізанням площинами, які проведені через центр сфери і вершини багатогранника. Сферичні сегменти можуть мати з одного боку ребра жорсткості вздовж їх сторін і фаски вздовж їх сторін з протилежного боку і можуть бути виконані, наприклад з холодноформованого склопластика. Пропонована сферична поверхня пояснюється наданими фігурами креслення: на Фіг.1 показана сферична поверхня, складена з п'яти і шестикутних сферичних сегментів; на Фіг.2-6 - правильні багатогранники, у тому числі на Фіг.2 - тетраедр, на Фіг.3 - куб, на Фіг.4 - октаедр, на Фіг.5 - ікосаедр, на Фіг.6 - додекаедр; на Фіг.7-19 - напівправи 6 7 Якщо розмір отриманих сферичних сегментів не відповідає певним вимогам, наприклад через велику складність виготовлення матриці по причині великих кутів ухилу виточки, зручність монтажусфери тощо, потрібні сферичні сегменти можна отримати їх поділом наступним чином. Ділять правильні сферичні багатокутники на декілька однакових багатокутників (не обов'язково правильних). При цьому, якщо в результаті поділу отримують геометричні фігури з принаймні однією віссю симетрії, для складання сферичної поверхні достатньо тільки одного типу сегменту, інакше буде потрібно два типи. Так, узявши за вихідний багатогранник - октаедр (Фіг.4) отримують повну 14881 8 сферичну поверхню з 8 однакових трикутних сферичних сегментів (Фіг.23) або - з 24 однакових чотирикутних сегментів (Фіг.24) або - з 48 трикутних сегментів двох типів (Фіг.25). Отримання сферичної поверхні з ікосаедра показано на Фіг.26-28, а зрізаного ікосаедра - на Фіг.29-31. Для отримання потрібних кутів огляду сферичну поверхню можна складати як частину повної сфери і за потреби, для надання певної форми доповнювати елементами, отриманими в результаті зрізання основних сегментів (Фіг.1). Отже сферична поверхня, згідно корисної моделі, має високу технологічність, якість поверхні і механічну міцність. 9 14881 10 11 14881 12 13 Комп’ютерна верстка Д. Шеверун 14881 Підписне 14 Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601