Спосіб відкритого розподілу секретних ключів у вигляді електронного коду на основі рекурентних послідовностей
Формула / Реферат
Спосіб відкритого розподілу секретних ключів у вигляді електронних кодів на основі рекурентних послідовностей, що включає відкритий канал передавання інформації у вигляді електронних кодів двох користувачів, які бажають отримати за допомогою відкритого каналу спільний секретний ключ у вигляді електронного коду на основі секретних частин у вигляді електронних кодів кожного користувача, який відрізняється тим, що для отримання спільного ключа у вигляді електронного коду використовують обчислення елементів рекурентних послідовностей з заданим індексом, а саме рекурентної ![]() - послідовності, яка визначається як послідовність чисел, що обчислюються за формулою vn.k = gkvn – 1,k + g1vn-k.k для початкових значень v0,k = 1, v1,k = g2 для порядку послідовності k = 2; v0,k =v1,k =,… = vk-3,k = 0, vk-2,k = 1, vk-1,k = gk для k>2; де g1, gk - цілі числа, n і k - цілі додатні числа, елементи
- послідовності, яка визначається як послідовність чисел, що обчислюються за формулою vn.k = gkvn – 1,k + g1vn-k.k для початкових значень v0,k = 1, v1,k = g2 для порядку послідовності k = 2; v0,k =v1,k =,… = vk-3,k = 0, vk-2,k = 1, vk-1,k = gk для k>2; де g1, gk - цілі числа, n і k - цілі додатні числа, елементи ![]() - послідовності vn+m,k для будь-яких цілих додатних n та m розраховуються за формулою
- послідовності vn+m,k для будь-яких цілих додатних n та m розраховуються за формулою
![]() , eлeмeнти
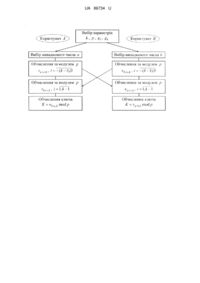
, eлeмeнти ![]() - послідовності vn▪m,k. для будь-яких цілих n та m обчислюються за допомогою способу прискореного обчислення цих елементів з використанням бінарного способу розкладання індексу m та формули обчислення елементів vn+m,k, при цьому розподіл секретного ключа відкритим каналом у вигляді електронного коду відбувається таким чином: спочатку центр довіри (або користувач А чи користувач В) виконує попередню процедуру вибору параметрів, для цього він вибирає параметр ρ як ціле додатне число, р>2, яке потім використовується як модуль під чаc обчислень елементів
- послідовності vn▪m,k. для будь-яких цілих n та m обчислюються за допомогою способу прискореного обчислення цих елементів з використанням бінарного способу розкладання індексу m та формули обчислення елементів vn+m,k, при цьому розподіл секретного ключа відкритим каналом у вигляді електронного коду відбувається таким чином: спочатку центр довіри (або користувач А чи користувач В) виконує попередню процедуру вибору параметрів, для цього він вибирає параметр ρ як ціле додатне число, р>2, яке потім використовується як модуль під чаc обчислень елементів ![]() - послідовності, вибирає цілі числа g1, gk і відкрито публікує їх разом з параметром ρ, під час безпосереднього розподілу ключа користувач А вибирає випадкове число a, 1<а<р, а користувач В вибирає випадкове число b, 1 < b < ρ, потім користувач А обчислює за модулем p va+i,k,
- послідовності, вибирає цілі числа g1, gk і відкрито публікує їх разом з параметром ρ, під час безпосереднього розподілу ключа користувач А вибирає випадкове число a, 1<а<р, а користувач В вибирає випадкове число b, 1 < b < ρ, потім користувач А обчислює за модулем p va+i,k, ![]() , а користувач В обчислює за модулем p νb+i,k,
, а користувач В обчислює за модулем p νb+i,k, ![]() , за допомогою способу прискореного обчислення елементів vn,k, з використанням бінарного способу розкладання індексу n та формули обчислення елементів vn+m,k, після чого користувачі А і В передають один одному обчислені елементи і розширюють отриманий один від одного набір елементів за допомогою формули, що визначає рекурентну
, за допомогою способу прискореного обчислення елементів vn,k, з використанням бінарного способу розкладання індексу n та формули обчислення елементів vn+m,k, після чого користувачі А і В передають один одному обчислені елементи і розширюють отриманий один від одного набір елементів за допомогою формули, що визначає рекурентну ![]() - послідовність, тобто користувач А таким чином обчислює за модулем p; елементи vh+i,k,
- послідовність, тобто користувач А таким чином обчислює за модулем p; елементи vh+i,k, ![]() , а користувач В обчислює за модулем p елементи va+i,k,
, а користувач В обчислює за модулем p елементи va+i,k, ![]() на завершення користувачі А і В обчислюють спільний ключ K у вигляді електронного коду відповідно як К = vb▪a,k mod p та К = va▪b,k mod p за допомогою способу прискореного обчислення елементів vn▪m,k. на основі відповідно своїх секретних чисел а і b та отриманих і обчислених за модулем ρ розширених наборів елементів відповідно vh+i,k,
на завершення користувачі А і В обчислюють спільний ключ K у вигляді електронного коду відповідно як К = vb▪a,k mod p та К = va▪b,k mod p за допомогою способу прискореного обчислення елементів vn▪m,k. на основі відповідно своїх секретних чисел а і b та отриманих і обчислених за модулем ρ розширених наборів елементів відповідно vh+i,k, ![]() , та va+i,k,
, та va+i,k, ![]() .
.
Текст
Реферат: UA 86734 U UA 86734 U 5 10 15 20 25 Корисна модель належить до техніки криптографічного захисту інформації і може використовуватися в системах захисту інформації, комп'ютерних мережах, банківських та електронних платіжних системах, системах стільникового зв'язку та інших інформаційнообчислювальних і телекомунікаційних системах. Відомий спосіб відкритого розподілу секретних ключів у вигляді електронних кодів, що базується на використанні операції піднесення до степеня великих чисел за модулем (W. Diffie, Μ.Ε. Hellman. New directions in cryptography // IEEE Transactions on Information Theory. - № 22, 1976. - P. 644-654). Суть способу полягає в тому, що спочатку центр довіри (або користувач А чи користувач В) вибирає і відкрито публікує просте число р та ціле число g, 2gp-2. Під час безпосереднього розподілу ключів користувач А вибирає випадкове число а, 1ар-2, а користувач В вибирає a випадкове число b, 1b р-2. Потім користувач А обчислює g mod p і передає його користувачу b В, а користувач В обчислює g mod p і передає його користувачу А. Після цього користувачі А і В b a a b отримують спільний секретних ключ К відповідно як К = (g ) mod p та К = (g ) У mod p. Стійкість способу базується на складності вирішення задачі дискретного логарифмування. Обчислювальна складність способу в основному визначається складністю виконання операцій піднесення до степеня великого числа за модулем. Всього, згідно зі способом, необхідно виконати чотири таких операції - по два на кожному боці. Відомий спосіб відкритого розподілу секретних ключів у вигляді електронних кодів, що базується на використанні математичного апарату рекурентних послідовностей (Р.Smith, M. Lennon, LUC: A new public-key system, Proceedings of the IFIP TC11, Nintli International Conference on Information Security: Computer Security, Toronto, May, 12-14, 1993. - P. 103-117). Суть способу (його іноді називають LUCDIF) полягає у використані рекурентної функції Люка і заміні піднесення до степеня за модулем, як це робиться в способі Діффі-Хеллмана, на обчислення елемента рекурентної послідовності Люка за модулем простого числа ρ з певним індексом. В способі використовуються рекурентні послідовності {Tn}, що отримуються з лінійного рекурентного співвідношення другого порядку такого вигляду. Tn=P▪Tn-1-Q▪Tn-2 (1) 30 35 40 де Ρ і Q взаємно прості числа. Серед набору послідовностей {Tn}, що породжуються рекурентним співвідношенням (1), n n виділяють послідовності {с1α +c2β ), де· с1 і с2 - будь-які числа, із значеннями початкових елементів T0=c1 +с2 та T1 = с1α + с2β. Спосіб базується на математичному апараті конкретного представника цієї послідовності, який позначається {Vn} і визначається таким чином: n n Vn = α + β , відповідно с1=1 = с2. Це є послідовність цілих чисел, оскільки її початкові елементи приймають такі значення V0=2, і V1 = Р. Ці послідовності залежать тільки від цілих чисел Ρ і Q, а функції, що їм відповідають, називають функціями Лука Ρ і Q. Іноді їх записують як Vn(P, Q), щоб підкреслити їхню залежність від Ρ і Q. Для цієї послідовності отримано таку аналітичну залежність: Vn▪k(P, 1) = Vn(Vk(P, 1),1) (2) 45 50 55 Основу способу складає залежність (2), яка дозволяє обчислювати елементи Vn(P, Q) послідовності різними шляхами. Згідно зі способом, на основі даного математичного апарату спочатку центр довіри (або один із користувачів) вибирає та відкрито публікує просте число p, а також число g, що задовольняє такій властивості. g 1and k /(p 1), Vk g,1 2 mod p k p 1 p . Під час безпосереднього розподілу ключів користувачі вибирають випадкові числа а і b, обчислюють відповідно Va{g, 1)mod p та Vb(g, 1)mod p та передають ці значення один одному. Після цього вони обчислюють кожен на своєму боці спільний ключ Κ, використовуючи залежність (2), як К = Vb (Va (g, 1)mod p, 1) mod p=Va (Vb (g, 1) mod p, 1) mod p. 1 UA 86734 U 5 10 15 Стійкість способу базується на складності обчислення індексу рекурентної Vn(P, Q) послідовності з обчисленого елемента цієї послідовності. Ця задача за обчислювальною складністю є аналогом задачі дискретного логарифмування, тому спосіб має схожі характеристики із способом Діффі-Хеллмана. Перевагою способу може бути те, що його стійкість не залежить від спроб криптоаналізу, які існують в задачах дискретного логарифмування. Відомий спосіб відкритого розподілу секретних ключів у вигляді електронних кодів, в основі якого використовується математичний апарат рекурентних послідовностей, що базуються на співвідношеннях, в яких початкові елементи пов'язані з коефіцієнтами (Яремчук Ю.Є. Використання рекурентних послідовностей для побудови криптографічних методів з відкритим ключем // Захист інформації. - №4, 2012. - С. 120-127). (найближчий аналог). Суть способу полягає у використані залежностей рекурентних послідовностей і заміні піднесення до степеня за модулем, як це робиться в способі Діффі-Xеллмана, на обчислення елемента рекурентної Uk.- послідовності з певним індексом. Uk - послідовність визначається рекурентним співвідношенням. un.k=gkun – 1,k+g1un-k.k (3) для початкових значень u0,k=g1, u1,k=g2, u2,k=g3, … uk-1,k=gk; де g1, g2, g3,…, gk - цілі числа; n і k - цілі додатні числа. 20 Елементи Uk - послідовності можуть обчислюватись через елементи v k - послідовності, яка визначається таким рекурентним співвідношенням. vn.k=gkvn-1.k+g1vn-1.k 25 (4) для початкових значень v0,k=1, v1,k=g2 для k=2; v0,k=v1,k =,… = vk-3,k=0, vk-2,k=1, vk-1,k=gk для k>2; де g1, gk - цілі числа; n і k - цілі додатні. Для будь-яких цілих додатних n, m та k отримано таку залежність. unm,k vm(k 2),k un,k g1 k 1 vm(k 2)i,k unk i,k (5) i 1 Для будь-яких цілих додатних n та k, таких що nk, отримано залежність, яка дозволяє 30 обчислювати елементи Uk - послідовності тільки на основі елементів v k - послідовності. un,k gk vn1,k g1 k 1 gi vni1,k (6) i 1 Спосіб відкритого розподілу ключів базується на використанні аналітичної залежності (5), яка дозволяє обчислити елемент un+m, k використовуючи елементи v k та Uk - послідовностей, 35 , причому зробити це двома шляхами: або використовуючи елементи vm+i, k, i 1 k 2 , та un-I, k, i 0,k 1 або використовуючи елементи vn+i, k, i 1 k 2 , та um-i, k, i 0,k 1 . , Згідно зі способом, під час безпосереднього розподілу ключів один користувач для будь якого вибраного ним випадкового числа а обчислює uа-i, k mod p, i 0,k 1 , а другий користувач 40 45 аналогічним чином обчислює ub-i, k mod p, i 0,k 1 , і, обмінявшись обчисленими значеннями, кожен з них отримує ключ К як ub+a, k mod p та ua+b, k mod p, продовжуючи обчислення на своєму боці за формулою (5), використовуючи відповідно свої числа а та b. При цьому значення ключа К є ключем розподілу, а числа а і b секретним ключем кожного користувача, причому а і b - це частини секретного ключа кожного користувача, оскільки попереднє отримання ключа розподілу будь-яким користувачем не можливе без отримання відповідної інформації від іншого користувача. Стійкість способу базується на складності вирішення задачі отримання індексу елемента рекурентної послідовності, обчисленого за модулем. Ця задача за рівнем складності 2 UA 86734 U 5 10 15 20 25 30 знаходиться приблизно на тому ж рівні, що і задача отримання числа степеня з результату модулярного піднесення до степеня, на якій базується стійкість способу Діффі-Хеллмана. Обчислювальна складність способу в основному визначається складністю обчислення за модулем елементу Uk - послідовності із заданим індексом. Рівень складності цих обчислень є приблизно таким же, що і рівень складності операції піднесення до степеня за модулем, на якому базується спосіб Діффі-Хеллмана. Виходячи з цього, спосіб розподілу ключів на основі Uk - послідовностей майже у два рази є більш швидким, ніж спосіб Діффі-Хеллмана, оскільки згідно першого способу необхідно виконувати два складних обчислення (по одному на кожному боці) елементу Uk - послідовності для заданих індексів, що представляються великими числами, замість чотирьох піднесень до степеня великого числа згідно способу Діффі-Хеллмана. Також перевагою способу на основі Uk - послідовностей є те, що в ньому забезпечується можливість збільшення стійкості пропорційно порядку k рекурентних послідовностей, що лежать в основі ключового розподілу, а також спрощення процедури завдання параметрів. Однак існують задачі, в яких дуже важливою є проблема забезпечення високого рівня стійкості криптографічних перетворень під час розподілу ключів. Це може бути навіть більш актуальним, ніж вирішення проблеми підвищення швидкості процедури розподілу ключів. В першу чергу, це стосується задач в системах захисту з підвищеним рівнем секретності. В цьому зв'язку, спосіб розподілу ключів на основі Uk - послідовностей, хоч і забезпечує достатній рівень криптографічної стійкості, але має потенційні можливості підвищення стійкості для відповідних систем захисту, оскільки отримання спільного ключа К на завершальному етапі розподілу здійснюється за допомогою аналітичної залежності обчислення елементу послідовності з адитивною, а не мультиплікативною зміною індексу, що могло б значно підвищити стійкість криптографічних перетворень під час розподілу ключів. В основу корисної моделі поставлено задачу створення способу відкритого розподілу секретних ключів у вигляді електронних кодів, в якому за рахунок використання в основі розподілу ключів математичного апарату тільки рекурентних v k - послідовностей та їх залежностей, досягається можливість підвищення стійкості криптографічних перетворень під час розподілу ключів. Поставлена задача вирішується тим, що використання для розподілу ключів математичного 35 апарату тільки на основі рекурентних v k - послідовностей забезпечує можливість користувачам на завершальному етапі розподілу обчислювати спільний ключ як результат обчислень елементу цієї послідовності за мультиплікативним способом зміни індексу. Оскільки отримання зловмисником складових частин індексу елемента послідовності обчисленого таким чином є більш складним, ніж отримання складових індексу елемента послідовності обчисленого за адитивним способом зміни індексу, це дасть можливість підвищити стійкість перетворень розподілу ключів. В основі способу пропонується використовувати таку аналітичну залежність послідовності: для будь-яких цілих додатних n, m та k. vk 40 unm,k v m(k 2),k vn,k g1 k 1 vm(k 2)i,k vnk i,k (7) i 1 Залежність (7) дозволяє обчислювати елемент vn+m, k на основі двох наборів елементів v k , послідовності: vn+i, k, i k 1,0 та vm+i, k, i 1 k 2 . Суть способу відкритого розподілу секретних ключів у вигляді електронних кодів, що 45 50 пропонується, базується на використанні властивості (7) v k - послідовності, яка забезпечує можливість організувати процедури прискореного обчислення елементів v k - послідовності для великих значень індексів, а саме процедури прискореного обчислення елементів vn, k та vn▪m, k. Спочатку центр довіри (або користувач А чи користувач В) вибирає і відкрито публікує ціле додатне число p (p>2) та цілі числа g1, gk. Під час безпосереднього розподілу ключів користувач А вибирає випадкове число а, 1
ДивитисяДодаткова інформація
Автори англійськоюYaremchuK Yurii Yevhenovych
Автори російськоюЯремчук Юрий Евгеньевич
МПК / Мітки
МПК: H03M 13/00
Мітки: коду, основі, відкритого, ключів, послідовностей, розподілу, вигляді, рекурентних, електронного, секретних, спосіб
Код посилання
<a href="https://ua.patents.su/7-86734-sposib-vidkritogo-rozpodilu-sekretnikh-klyuchiv-u-viglyadi-elektronnogo-kodu-na-osnovi-rekurentnikh-poslidovnostejj.html" target="_blank" rel="follow" title="База патентів України">Спосіб відкритого розподілу секретних ключів у вигляді електронного коду на основі рекурентних послідовностей</a>
Попередній патент: Фільтр
Наступний патент: Спосіб шифрування інформації з відкритим ключем у вигляді електронного коду на основі рекурентних послідовностей
Випадковий патент: Мішалка