Спосіб генерування та перевіряння цифрового підпису у вигляді електронного коду з використанням рекурентних послідовностей

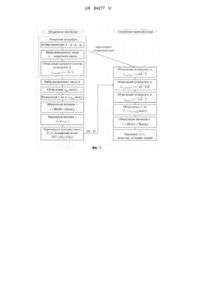
Реферат: UA 84277 U UA 84277 U 5 10 Корисна модель належить до техніки криптографічного захисту інформації і може використовуватися в системах захисту інформації, комп'ютерних мережах, банківських та електронних платіжних системах, системах стільникового зв'язку та інших інформаційнообчислювальних і телекомунікаційних системах. Відомий спосіб цифрового підписування, що базується на використанні операції піднесення до степеня великих чисел за модулем [Т. ElGamal, "A Public-Key Cryptosystcm and a Signature Scheme Based on Discrete Logarithms", Advances in Cryptology: Proceedings of CRYPTO 84, Springer Verlag, 1985, pp. 1-18.] Суть способу полягає в тому, що на попередньому етапі центр довіри або відправник (підписант) вибирає і відкрито публікує просте число p та ціле число g , 1  g  p . Потім він вибирає випадкове число a , 1  a  p  2 , як секретний ключ та обчислює y  ga mod p відкритий ключ, який передається одержувачу (перевіряльнику). Після цього протокол цифрового підписування реалізується таким чином. На етапі формування підпису підписант вибирає випадкове число k , 1  k  p  2 і 15 НОД k,p  1  1 та обчислює r  gk mod p (ці обчислення можуть бути виконані і попередньо). Потім він обчислює s  k 1h(M)  a  r mod p  1 , де h - функція хешування, і надсилає повідомлення M з підписом r, s одержувачу. 20 На етапі перевірки підпису перевіряльник спочатку перевіряє чи 0  r  p та 0  s  p  1 і, якщо хоча б одна умова не виконується, то підпис відкидається. А потім, якщо обидві ці умови виконуються, підпис приймається тоді і лише тоді, коли виконується рівняння 25 gh(M) mod p  y r r s mod p . Стійкість способу базується на складності вирішення задачі дискретного логарифмування. Обчислювальна складність способу в основному визначається складністю виконання операцій піднесення до степеня великого числа за модулем. Всього згідно з способом необхідно виконати чотири таких операції - по дві на кожному боці: з боку відправника обчислення на попередньому етапі відкритого ключа y  ga mod p та значення r  gk mod p , з 30 боку одержувача - y r mod p та r s mod p . Відомий спосіб цифрового підписування, що базується на використанні операції піднесення до степеня великих чисел за модулем [С.Р. Schnorr. "Efficient Signature Generation for Smart Cards". Advances CRYPTO '89 Proceedings, Springer-Verlag, 1990, pp. 239-252]. Суть способу полягає в тому, що він базується на тих же обчисленнях, що і розглянутий перед цим спосіб Ель-Гамаля, і є одним з варіантів цього способу. На попередньому етапі центр довіри або відправник вибирає і відкрито публікує два простих числа p і q : q p  1 та число g  1 : g q  1mod p  . Потім він вибирає випадкове число a  q як 35 40 45 50 секретний ключ та обчислює y  g a mod p - відкритий ключ, який передається одержувачу. Після цього протокол цифрового підписування реалізується таким чином. На етапі формування підпису відправник вибирає випадкове число k  q та обчислює x  gk mod p (ці обчислення можуть бути виконані і попередньо). Далі, з отриманого значення x та повідомлення M , що підписується, він здійснює хешування за допомогою функції h , обчислюючи значення s  k  a  r  mod q . Потім відправник обчислює s=(k+a-r)modq і надсилає повідомлення M з підписом r, s одержувачу. На етапі перевірки підпису одержувач обчислює x'  gs  y r mod p і перевіряє, чи виконується рівняння r  hx' ,M . Якщо так, то підпис приймається, інакше - відкидається. Стійкість способу базується на складності вирішення задачі дискретного логарифмування. Обчислювальна складність способу, як і в попередньому способі, в основному визначається складністю виконання операцій піднесення до степеня великого числа за модулем, яких так само необхідно виконувати чотири - по дві на кожному боці. Відомий спосіб цифрового підписування, що базується на використанні математичного апарату рекурентних послідовностей (P. Smith, С. Skinner, A public-key cryptosystem and a digital signature system based on the Lucas function analogue to discrete logarithms, in Advances in Cryptology-Asiacrypt 1994, Lect. Notes in Соmр. Sci. 917. Springer, Berlin, 1995, 357-364.) (найближчий аналог). 1 UA 84277 U 5 Суть способу (його іноді називають LUCELG DS) полягає у використані рекурентної функції Люка і заміні піднесення до степеня за модулем, як це робиться в способі Ель-Гамаля та його варіантах, на обчислення елементу рекурентної послідовності Люка за модулем простого числа p з певним індексом. В способі використовуються рекурентні послідовності Tn  , що отримуються з лінійного рекурентного співвідношення другого порядку такого вигляду Tn  P  Tn 1  Q  Tn  2 , 10 (1) де P і Q взаємно прості числа. Серед набору послідовностей Tn  , що породжуються рекурентним співвідношенням (1),   виділяють послідовності c 1 n  c 2n , де c 1 і c 2 - будь-які числа, із значеннями початкових елементів T0  c1  c 2 та T1  c1  c 2 . Спосіб базується на математичному апараті двох конкретних представників цієї послідовності, які позначаються Un  та Vn  і визначаються таким чином: 15 20 Un   n  n , відповідно 1 c1   c 2 ;     Vn   n  n , відповідно c1  1  c 2 . Це є послідовності цілих чисел, оскільки їх початкові елементи приймають такі значення U0  0 , U1  1, V0  2 , і V1  P . Ці послідовності залежать тільки від цілих чисел P і Q , а функції, що їм відповідають, називають функціями Люка P і Q . Іноді їх записують як Un P, Q та Vn P, Q , щоб підкреслити їхню залежність від P і Q . Для цих послідовностей отримано такі аналітичні залежності: Vnk P,1  Vn Vk P,1,1 , (2)   2Vn  m  Vn Vm  DU nUm  2  n  m  n  m , (3) 25 30 Спосіб цифрового підписування базується на даному математичному апараті і по суті є еквівалентом способу Ель-Гамаля. Основу способу складають аналітичні залежності (2) і (3), що дозволяють обчислювати елементи Un P, Q та Vn P, Q - послідовностей різними шляхами. На попередньому етапі цифрового підписування центр довір або відправник генерує та публікує просте число p , використовуючи такий генератор, що Vp 1 / t ,1  2 mod p для кожного t  1 поділеного на p  1 . Потім він вибирає випадкове число x  p як секретний ключ та отримує відкритий ключ у вигляді двох значень y та y' , що обчислюються як 35 40 y  Vx ,1mod p та y'  Ux ,1mod p , які передаються одержувачу. Після цього протокол цифрового підписування реалізується таким чином. На етапі формування підпису відправник вибирає випадковим чином секретне число k , 0  k  p , для кожного повідомлення (або блока повідомлення) m і обчислює r  Vk ,1mod p та r'  Uk ,1mod p . Потім він обчислює s як s  k 1m  x  r mod p  1 і надсилає цифровий підпис у вигляді m,r,r' , s одержувачу. На етапі перевірки підпису одержувач, по аналогії із способом Ель-Гамаля, спочатку обчислює ліву частину LHS  як LHS  Vm ,1mod p , потім, дещо складніше ніж в Ель-Гамаля, обчислює праву частину RHS  як RHS  Vr y,1Vs r,1  Dy ' Ur y,1r' Us r,1/ 2 mod p , 45 де D  2  4 mod p . Якщо RHS LHS , тоді четвірка m,r,r' , s вважається справжнім підписом способу LUCELG DS, інакше - підпис відкидається. 2 UA 84277 U 5 10 15 20 25 30 35 40 Стійкість способу базується на складності обчислення індексу рекурентної послідовності з обчисленого елементу цієї послідовності. Ця задача за обчислювальною складністю є аналогом задачі дискретного логарифмування. Тому спосіб має схожі характеристики з тими способами цифрового підписування, що базуються на дискретному логарифмуванні. Однак перевагою є те, що стійкість способів цифрового підписування на основі розглянутого математичного апарату рекурентних послідовностей не залежить від спроб криптоаналізу, що існують в задачах дискретного логарифмування. Недоліком цього способу цифрового підписування, який є найближчим аналогом, є те, що він має певні слабкості щодо стійкості, зокрема розглянуті функції Люка є вразливими до екзистенційної підробки. Хоча при цьому вважається, що способи, які базуються на цих функціях, в цілому є більш стійкими, ніж ті, що базуються на математичному апараті еліптичних кривих. Однак, основним недоліком цього способу є те, що він має велику обчислювальну складність, оскільки потребує значно більшої кількості обчислень елементів рекурентних послідовностей, ніж навіть аналоги, що базуються на операції піднесення до заданого степеня. Загальним недоліком розглянутих способів цифрового підписування є те, що існують задачі, для яких важливим є швидке виконання саме процедури формування підпису, тому складні обчислення, що виконуються в процедурі формування підпису згідно з існуючими способами цифрового підписування створюють підписанту певні незручності, в зв'язку з чим актуальним є прискорення виконання процедури формування підпису при забезпеченні достатнього рівня криптостійкості. В основу корисної моделі поставлено задачу створення способу цифрового підписування на основі математичного апарату більш узагальнених рекурентних послідовностей, ніж розглядались раніше при побудові способів такого типу, коли для отримання цифрового підпису у вигляді електронного коду використовуються обчислення елементів рекурентних послідовностей з певним індексом на основі узагальнених рекурентних залежностей з коефіцієнтами, що пов'язані з початковими елементами послідовностей, в яких коефіцієнти рекурентних залежностей, початкові елементи та елементи послідовностей, що породжуються цими залежностями, можуть бути будь-якими цілими числами без додаткових умов та обмежень. За рахунок цього досягається можливість зменшення обчислювальної складності процедури формування підпису. Крім того забезпечується можливість збільшення стійкості пропорційно порядку рекурентних послідовностей, що лежать в основі цифрового підписування, а також спрощення процедури завдання параметрів. Поставлена задача вирішується тим, що використання в основі цифрового підписування математичного апарату більш узагальнених рекурентних послідовностей, ніж у найближчому аналогу, дозволяє отримати аналітичні залежності для різного роду обчислень елементів цих послідовностей з властивостями, які забезпечують кращі можливості щодо спрощення обчислень цифрового підписування, що, в першу чергу, може бути використано для спрощення обчислень процедури формування підпису при розробці способу цифрового підписування. Зокрема, пропонується як математичний апарат рекурентних послідовностей використовувати апарат рекурентних Vk -послідовностей, які є узагальненими рекурентними послідовностями, при обчисленні елементів яких використовуються рекурентні залежності з коефіцієнтами, що пов'язані з початковими елементами послідовностей.   Vk -послідовністю назвемо послідовність, яка складається з Vk -послідовності та Vk послідовності. 45  Vk -послідовністю назвемо послідовність чисел, що обчислюються за формулою  n,k  gk  n 1,k  g1 n  k,k , (4) для початкових значень 0,k  1 , 1,k  g2 для k  2 ;  0,k  1,k  ...  k  3,k  0 ,  k  2,k  1 ,  k 1,k  gk для k  2 ; де g1 , gk - цілі числа; n і k - цілі додатні. 50 Обчислення елементів цієї послідовності для спадних n , починаючи з деякого значення n  l , буде здійснюватись таким чином  n,k   n  k,k  gk   n  k 1,k , g1 (5) 3 UA 84277 U  Vk -послідовністю назвемо послідовність чисел, що обчислюються за формулою (5) для n   від'ємних при початкових значеннях  1,k  0 ,   2,k  g1 1 для k  2 ;  1,k  0 ,   2,k  g1 1 ,   3,k    4,k  ...   k,k  0 для k  2 . Для будь-яких цілих додатних n , m та k отримано таку аналітичну залежність 5  n  m,k   m  (k  2),k   n,k  g1  k 1   m  (k  2) i,k   n k  i,k , (6) i 1 Для будь-яких цілих додатних n і m , таких що 1  m  n та будь-якого цілого додатного k отримано таку залежність  n  m,k    m  (k  2),k   n,k  g1  k 1   m  (k  2) i,k   n k  i,k , (7) i 1 10 Суть способу цифрового підписування, що пропонується, базується на використанні властивості (6) Vk -послідовності, яка дозволяє використовувати її для обчислення елементу  n m,k , а також для обчислення елементу   n m,k . Крім того властивість (6) дозволяє 15 реалізувати процедуру обчислення елементу  nm,k . Так само на основі властивості (7) можна реалізувати процедуру обчислення елементу  nm,k . Все це дає можливість створення такого 20 способу цифрового підписування. Спочатку відправник-підписант (або центр довіри) виконує попередню процедуру вибору параметрів та обчислення ключів. При цьому він випадковим чином вибирає секретний ключ a , за допомогою якого обчислює, а потім передає одержувачу-перевіряльнику відкритий ключ   a i,k , i   k,1 При формуванні цифрового підпису для повідомлення M відправник-підписант вибирає випадкове число b , обчислює  b,k , визначає значення x як x   b,k та обчислює значення r як r  h(M)  x mod p за допомогою вибраної функції хешування h від повідомлення M . Далі він 25 визначає значення s як s  b  a  r . Після цього отриману множину цілих чисел r; s він перетворює у цифровий підпис вигляду DS  0 r 0 s і передає його разом з повідомленням M одержувачу. При перевірці цифрового підпису одержувач спочатку обчислює   ar  i,k , i   k  1,0 , на   основі відкритого ключа - елементів   a i,k , i   k, k  2 та отриманого від підписанта значення r , а потім на основі обчислених щойно елементів та отриманого від підписанта значення s він 30 35 40 обчислює елементи  s i,k , i   1 k  2 . , Після цього на основі усіх обчислених підписантом елементів він обчислює значення x' як x'    ar  s,k , використовуючи залежність (6), а потім обчислює значення r' як r'  h(M)  x'mod p та перевіряє, чи виконується r  r' . Якщо так, то підпис приймається, в іншому випадку відкидається. Не важко пересвідчитись, що для підпису, згенерованого згідно з цим методом, перевірка r  r' завжди буде виконуватись. Загальна схема способу цифрового підписування на основі математичного апарату рекурентних послідовностей, що пропонується, буде мати вигляд, представлений на фігурі 1. Операція за модулем в схемі цифрового підписування використовується для обмеження розрядності чисел під час виконання арифметичних операцій. Обчислення елементу  b,k mod p відправник може виконати попередньо, заздалегідь до безпосереднього формування цифрового підпису з повідомлення M . В запропонованому методі цифрового підписування основні обчислення виконуються згідно з залежністю (6). Обчислення елементу  n m,k згідно з цією залежністю здійснюється на основі 45 елементів  n i,k , i   k  1,0 та елементів  m i,k , i   1 k  2 . , 4 UA 84277 U 5 10 В разі необхідності отримання певного послідовного набору елементів Vk -послідовності у кількості, більшої ніж k , достатньо отримати будь-які послідовні k з них, оскільки інші можуть бути обчислені згідно з формулами (4) або (5) на основі вже отриманих. Виходячи з вищесказаного отримаємо такий протокол цифрового підписування на основі елементів Vk -послідовності. Крок 1. Задати параметр k . Крок 2. Вибрати p . Крок 3. Вибрати g1 , g2 . Крок 4. Відправнику передати параметри Одержувачу. Крок 5. Відправнику вибрати випадкове число a - секретний ключ. Крок 6. Відправнику обчислити відкритий ключ за модулем p   a i,k , i   k, k  2 , використовуючи алгоритм прискореного обчислення елементів  n,k для від'ємних значень n . Крок 7. Відправнику передати відкритий ключ   a i,k mod p , i   k,1 Одержувачу. 15 20 Крок 8. Одержувачу обчислити за модулем p   a i,k , i  0,k  2 , за формулою (4). Крок 9. Відправнику вибрати випадкове число b . Крок 10. Відправнику обчислити b,k mod p , використовуючи алгоритм прискореного обчислення елементів  n,k для додатних значень n . Крок 11. Відправнику визначити x як x  b,k mod p . Крок 12. Відправнику обчислити значення r як r  h(M)  x mod p за допомогою вибраної функції хешування h від повідомлення M та значення x . Крок 13. Відправнику визначити значення s як s  b  a  r . Крок 14. Відправнику перетворити множину цілих чисел r; s у цифровий підпис вигляду   DS  0 r 0 s і передати його разом з повідомленням M Одержувачу. 25 Крок 15. Одержувачу обчислити за модулем p алгоритм прискореного обчислення елементів  mn,k .   ar  i,k , i   k  1,0 , використовуючи Крок 16. Одержувачу обчислити за модулем p елементи  s i,k , i   1 k  2 , використовуючи , алгоритм прискореного обчислення елементів  n,k для додатних значень n . 30 35 Крок 17. Одержувачу обчислити x'    ar  s,k mod p згідно з залежністю (6). Крок 18. Одержувачу обчислити значення r' як r'  h(M)  x'mod p . Крок 19. Одержувачу перевірити, чи виконується r  r' , якщо так, то підпис вважати вірним. Технічний результат: забезпечено можливість збільшення стійкості пропорційно порядку рекурентних послідовностей, що лежать в основі цифрового підписування; спрощено процедуру завдання параметрів; зменшено майже вдвічі обчислювальну складність процедури формування підпису і, як наслідок, суттєво збільшено швидкодію процедури формування підпису, що дає можливість розширення галузі використання таких способів цифрового підписування. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 40 45 Спосіб генерування та перевіряння цифрового підпису у вигляді електронного коду на основі рекурентних послідовностей, що включає процедури генерування та перевіряння цифрового підпису у вигляді електронного коду, секретний ключ та обчислений на його основі відкритий ключ підписанта, який відрізняється тим, що для отримання цифрового підпису у вигляді електронного коду використовують обчислення елементів рекурентних послідовностей з  заданим індексом, а саме рекурентної Vk -послідовності, яка складається з Vk -послідовності та   Vk -послідовності, Vk -послідовність визначається як послідовність чисел, що обчислюються за формулою: n,k  gk n 1,k  g1n k,k для початкових значень  0,k  1, 1,k  g2 для порядку послідовності k  2 ;  0,k  1,k  ...  k  3,k  0 ,  k  2,k  1 ,  k 1,k  gk для k  2 ; де g1 , gk  цілі числа; n і k - цілі додатні числа, Vk -послідовність визначається як послідовність чисел, що 5 UA 84277 U обчислюються за формулою:  n,k   n  k,k  gk   n  k 1,k - від'ємних при початкових n g1   значеннях  1,k  0 ,   2,k  g1 1 для k  2 ;  1,k  0 ,   2,k  g1 1 ,   3,k    4,k  ...   k,k  0 для k  2 , елементи Vk -послідовності  n m,k для будь-яких цілих n та m розраховуються за формулою: 5 10  n  m,k   m  (k  2),k   n,k  g1  k 1   m  (k  2) i,k   n k  i,k Vk -послідовності  nm,k для , i 1 будь-яких цілих n та m обчислюються за допомогою способу прискореного обчислення цих елементів з використанням бінарного способу розкладання індексу m та формули обчислення елементів  n m,k , при цьому генерування та перевіряння цифрового підпису у вигляді електронного коду відбувається таким чином: спочатку відправник-підписант (або центр довіри) виконує попередню процедуру вибору параметрів та обчислення ключів у вигляді електронних кодів, для цього він вибирає параметр p як ціле додатне число, p  2 , яке потім використовується як модуль під час обчислень елементів Vk -послідовності, далі він випадковим чином вибирає секретний ключ a , 1  a  p , який він використовує для обчислення відкритого ключа   a i,k mod p , i   k,1, за допомогою способу прискореного обчислення елементів 15 20  n,k з використанням бінарного способу розкладання індексу n , і передає одержувачу-перевіряльнику обчислений відкритий ключ, при генеруванні цифрового підпису у вигляді електронного коду для повідомлення M відправник-підписант вибирає випадкове число b , 1  b  p , обчислює елемент  b,k mod p за допомогою способу прискореного обчислення елементів  n,k , визначає значення x як x  b,k mod p та обчислює значення r , представлене у вигляді електронного коду, як r  h(M)  x mod p за допомогою вибраної функції хешування h у діапазоні чисел, що обмежуються p  1, від повідомлення M та значення x , далі він визначає значення s як s  b  a  r , після чого отриману множину цілих чисел r; s він перетворює у  цифровий підпис як електронний код у вигляді DS  0 r 0 s  і передає його разом з повідомленням M одержувачу, при перевірці цифрового підпису у вигляді електронного коду одержувач спочатку обчислює за модулем p елементи   ar  i,k , i   k  1,0 , на основі 25 відкритого ключа - елементів   a i,k mod p , i   k, k  2 та отриманого від підписанта значення r за допомогою способу прискореного обчислення елементів  nm,k , а потім на основі , отриманого від підписанта значення s він обчислює за модулем p елементи  s i,k , i   1 k  2 , за допомогою способу прискореного обчислення елементів  n,k , після цього на основі усіх обчислених підписантом елементів він обчислює значення x' як x'    ar  s,k mod p , 30 використовуючи формулу обчислення елементів  n m,k , a потім обчислює значення r' у вигляді електронного коду як r'  h(M)  x'mod p та перевіряє, чи виконується рівняння r  r' , якщо так, то підпис приймається, в іншому випадку - відкидається. 6 UA 84277 U Комп’ютерна верстка Л. Ціхановська Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 7