Спосіб оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад
Номер патенту: 55212
Опубліковано: 10.12.2010
Автори: Андреєв Олександр Володимирович, Гузій Микола Миколайович, Андреєв Володимир Ілліч, Ігнатов Володимир Олексійович
Формула / Реферат
1. Спосіб оптимальної екстраполяції нестаціонарних випадкових сигналів на тлі завад, у якому для оптимальної екстраполяції нестаціонарного випадкового сигналу на тлі завади використовують метод максимальної правдоподібності, а також декілька попередніх результатів вимірювань зашумленого сигналу з апріорно відомими ймовірнісними характеристиками (математичні очікування, дисперсії, кореляційні функції сигналу та завади), який відрізняється тим, що спосіб передбачає визначення оптимального прогнозованого (екстрапольованого) значення випадкового нестаціонарного сигналу на тлі завад за критерієм мінімуму дисперсії похибки.
2. Спосіб оптимальної екстраполяції нестаціонарних випадкових сигналів на тлі завад за п. 1, який відрізняється тим, що оптимальну оцінку ![]() для майбутнього моменту часу
для майбутнього моменту часу ![]() екстрапольованого значення випадкового нестаціонарного сигналу
екстрапольованого значення випадкового нестаціонарного сигналу
![]() ,
,
що спостерігають на тлі завади ![]() у два попередні моменти часу
у два попередні моменти часу ![]() у вигляді зашумленого сигналу
у вигляді зашумленого сигналу
![]() ,
,
де ![]() , детерміновані параметри
, детерміновані параметри ![]() задання нелінійності і нестаціонарності випадкового сигналу
задання нелінійності і нестаціонарності випадкового сигналу ![]() задовольняють умовам:
задовольняють умовам:
![]() ,
,
коефіцієнти ![]() є випадковими незалежними величинами, що мають гаусівські розподіли з математичними очікуваннями і дисперсіями:
є випадковими незалежними величинами, що мають гаусівські розподіли з математичними очікуваннями і дисперсіями:
![]() ,
,
заваду (шум) ![]() представляють як випадковий стаціонарний гаусівський сигнал з характеристиками
представляють як випадковий стаціонарний гаусівський сигнал з характеристиками
![]() ,
,
визначають за двома попередніми вимірюваннями ![]() та
та ![]() за формулою непрямих вимірювань:
за формулою непрямих вимірювань:
![]() ,
,
де значення параметра ![]() вибирають оптимальним способом із необхідних умов
вибирають оптимальним способом із необхідних умов
![]()
мінімізації дисперсії похибки екстраполяції
![]()
екстрапольованого значення ![]() за формулою непрямих вимірювань :
за формулою непрямих вимірювань :
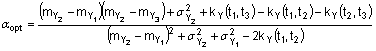 ,
,
де ![]() - математичні сподівання сигналів
- математичні сподівання сигналів ![]() , що спостерігаються в моменти часу
, що спостерігаються в моменти часу ![]() , що обчислюються при
, що обчислюються при ![]() за формулою
за формулою
![]() ,
,
де ![]() - математичні сподівання випадкових параметрів
- математичні сподівання випадкових параметрів ![]() ,
,
![]() - параметр нелінійності випадкового нестаціонарного сигналу, що екстраполюється (ВНС),
- параметр нелінійності випадкового нестаціонарного сигналу, що екстраполюється (ВНС),
![]() - дисперсія випадкового нестаціонарного сигналу
- дисперсія випадкового нестаціонарного сигналу ![]() в і-ті моменти часу,
в і-ті моменти часу,
![]() - кореляційна функція ВНС
- кореляційна функція ВНС ![]() для і-го та j-го моментів спостереження, що забезпечує мінімальне значення дисперсії похибки оптимальної екстраполяції, яка розраховується за формулою непрямих вимірювань
для і-го та j-го моментів спостереження, що забезпечує мінімальне значення дисперсії похибки оптимальної екстраполяції, яка розраховується за формулою непрямих вимірювань
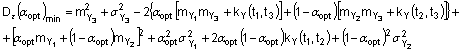 .
.
3. Спосіб оптимальної екстраполяції нестаціонарних випадкових сигналів на тлі завад за п. 1, який відрізняється тим, що дисперсію оптимальної оцінки ![]() отримують за формулою непрямих вимірювань
отримують за формулою непрямих вимірювань
![]() .
.
4. Спосіб оптимальної екстраполяції нестаціонарних випадкових сигналів на тлі завад за п. 1, який відрізняється тим, що ефективність оптимального способу екстраполяції оцінюють за формулами непрямих вимірювань - відношенням сигнал/шум на виході оптимального екстраполятора
![]() ,
,
де ![]() - дисперсія значення випадкового сигналу, що буде спостерігатися у момент часу
- дисперсія значення випадкового сигналу, що буде спостерігатися у момент часу ![]() ,
,
![]() - мінімальна дисперсія похибки екстраполяції,
- мінімальна дисперсія похибки екстраполяції,
відношенням дисперсії випадкового сигналу, що буде спостерігатися у момент часу ![]() , до дисперсії екстрапольованого оптимального значення сигналу
, до дисперсії екстрапольованого оптимального значення сигналу ![]()
![]() ,
,
відношенням різниці між дисперсією випадкового сигналу, що спостерігається у момент часу ![]() , та дисперсією екстрапольованого сигналу
, та дисперсією екстрапольованого сигналу ![]() до мінімальної дисперсії похибки екстраполяції
до мінімальної дисперсії похибки екстраполяції
![]() .
.
Текст
1. Спосіб оптимальної екстраполяції нестаціонарних випадкових сигналів на тлі завад, у якому для оптимальної екстраполяції нестаціонарного випадкового сигналу на тлі завади використовують метод максимальної правдоподібності, а також декілька попередніх результатів вимірювань зашумленого сигналу з апріорно відомими ймовірнісними характеристиками (математичні очікування, дисперсії, кореляційні функції сигналу та завади), який відрізняється тим, що спосіб передбачає визначення оптимального прогнозованого (екстрапольованого) значення випадкового нестаціонарного сигналу на тлі завад за критерієм мінімуму дисперсії похибки. 2. Спосіб оптимальної екстраполяції нестаціонарних випадкових сигналів на тлі завад за п. 1, який Yt Xt де q t , 1, детерміновані параметри 0 1, 0 1 2, коефіцієнти a0 , a1 є випадковими незалежними величинами, що мають гаусівські розподіли з математичними очікуваннями і дисперсіями: 2 ;M a 2, M a0 m0 ; D a0 1 m1; D a1 0 1 заваду (шум) t представляють як випадковий стаціонарний гаусівський сигнал з характеристиками M t m 0 , M t1 , t 2 k t , мінімізації дисперсії похибки екстраполяції D D M Y3 Y2 Y1 Y2 2 , opt 2 Y2 m Y3 mY 2 mY 2 1 k Y t1, t 3 2 Y2 2 Y1 k Y t1, t 2 k Y t 2, t 3 , 2k Y t1, t 2 (13) (19) дні моменти часу t1 , t 2 у вигляді зашумленого сигналу за формулою UA екстрапольованого значення Y3 непрямих вимірювань: 55212 Y3 Y2 Y1 Y2 , де значення параметра вибирають оптимальним способом із необхідних умов 2D Y D Y3 3 0, 0, 2 (11) визначають за двома попередніми вимірюваннями Y1 Y t1 та Y2 Y t 2 за формулою непрямих вимірювань: U 0 майбутнього моменту часу t3 екстрапольованого значення випадкового нестаціонарного сигналу q Xt it i , i 0 що спостерігають на тлі завади t у два попере m Y1 m Y2 задання нелінійності і нестаціонарності випадкового сигналу x t задовольняють умовам: відрізняється тим, що оптимальну оцінку Y3 для m Y2 0, 1 3 55212 де m yi - математичні сподівання сигналів Yi , що спостерігаються в моменти часу t i , що обчислюються при 0 my i m0 1 2 за формулою 0, 1 m1t , i де m0 ,m1 - математичні сподівання випадкових параметрів a0 , a1 , - параметр нелінійності випадкового нестаціонарного сигналу, що екстраполюється (ВНС), D m2 Y3 opt min optm Y1 1 2 Y3 opt m Y2 2 opt m Y m Y 1 3 2 2 2 opt Y1 4 2 - дисперсія випадкового нестаціонарного сигYi налу y в і-ті моменти часу, k Y t i , t j - кореляційна функція ВНС Y t для і-го та j-го моментів спостереження, що забезпечує мінімальне значення дисперсії похибки оптимальної екстраполяції, яка розраховується за формулою непрямих вимірювань k Y t1, t 3 2 opt 1 1 opt m Y2 m Y3 opt k Y t1, t 2 1 opt k Y t 2, t3 2 2 . Y2 3. Спосіб оптимальної екстраполяції нестаціонароцінки Y3 отримують за формулою непрямих них випадкових сигналів на тлі завад за п. 1, який вимірювань відрізняється тим, що дисперсію оптимальної 2 2 2 2 D Y3 1 opt 2 opt 1 opt k Y t1, t 2 . opt Y1 Y2 4. Спосіб оптимальної екстраполяції нестаціонарних випадкових сигналів на тлі завад за п. 1, який відрізняється тим, що ефективність оптимального способу екстраполяції оцінюють за формулами непрямих вимірювань - відношенням сигнал/шум на виході оптимального екстраполятора D Y3 , h1 D min де D Y3 - дисперсія значення випадкового сигналу, що буде спостерігатися у момент часу t 3 , D min - мінімальна дисперсія похибки екстрапо сії екстрапольованого оптимального значення сигналу D Y3 h2 D Y3 , D Y3 відношенням різниці між дисперсією випадкового сигналу, що спостерігається у момент часу t 3 , та дисперсією екстрапольованого сигналу D Y3 до мінімальної дисперсії похибки екстраполяції ляції, відношенням дисперсії випадкового сигналу, що буде спостерігатися у момент часу t 3 , до диспер h3 Корисна модель належить до теорії випадкових процесів та використання цієї теорії для розв'язання прикладних задач надійності, діагностування, контролю якості, обробки сигналів на тлі завад, контролю працездатності та прогнозуванні трафіку обчислювальних мереж, при макропрогнозуванні трендів в економіці при малих обсягах вибірок в часових рядах. Аналогом запропонованого способу є винахід, який відноситься до способів керування декількома випадковими нестаціонарними процесами за допомогою адаптивної оцінки і збору інформації [1]. Більш конкретно, цей винахід стосується адаптивного пристрою контролю, в якому моніторинг минулих станів процесів використовується для екстраполяції поточного стану кожного процесу, що контролюється, а також для оцінки факторів невизначеності в кожному процесі. Недоліком є те, що не враховується дія завади. Аналогом запропонованого способу є також спосіб покращення зображення нелінійною екстраполяцією в частотному просторі [2]. У ньому вхідне зображення збільшується для того, щоб включити просторові частотні вузли, які мають частоти вищі ніж ті, що входять у вхідне зображення. Карта перетинів будується на основі вхідного зображення з використанням високоякісної прохідної фільтрувальної техніки. Збільшена карта створюється за допомогою використання нелінійного оператора до карти перетинів із збереженням фазових переходів перетинів вхідного зображення. Збільшена карта додається до вхідного зображення, щоб отримати результуюче зображення, яке має просторові частоти, більші ніж у вхідному зображенні. Простота обчислень і легкість реалізації дозволяють отримати покращене зображення в D Y3 D Y3 D min . 5 реальному часі для таких додатків як відеофони, покращення телевізійного зображення, реставрація старих фільмів. Недоліком способу є те, що в описі патенту не показано, як працює запропонований спосіб при впливі на зображення випадкової завади. Крім того, цей спосіб вимагає відносно великих обсягів спостережень для отримання спектра. Аналогом запропонованого способу є також метод синусоїдального моделювання та прогнозу швидко замираючих процесів при федінгу радіосигналів [3]. Пропонується метод прогнозування швидко замираючих процесів з використанням синусоїдальних методів моделювання. В методі спочатку використовується низькочастотна фільтрація поступаючого сигналу, що збільшує потужність зникаючого сигналу до потужності шуму. Використовується частотна оцінка основної гармоніки і розробляється синусоїдальна модель зникаючого процесу. Ця модель використовується для покращення характеристик часових схем обробки і зменшення ефекту зникнення. Недоліком є те, що не мінімізується дисперсія похибки прогнозування сигналу. Прототипом корисної моделі обрана функція прогнозування Predict системи MathCAD. Вона дозволяє по ряду відомих рівномірно розташованих попередніх точок функції розрахувати деяке число N наступних точок функції і, по суті, виконувати екстраполяцію довільної (але достатньо гладкої і передбачуваної) залежності. Функція передбачення має такий вигляд: predict (data і, k, N), де data і - вектор даних, розмірності i, k - ступінь поліному регресії, N - кількість точок екстраполяції. Ця функція екстраполяції забезпечує високу точність при монотонних функціях, які можуть бути представлені поліномами невисокого ступеню. Недоліками цього способу екстраполяції є те, що необхідно обирати математичну модель регресії; визначати велику кількість (90...100) точок вхідної залежності. Спосіб не враховує наявність випадкових завад. В основу корисної моделі, що пропонується, поставлено задачу визначення оптимального вагового коефіцієнта opt за критерієм мінімуму дисперсії minD( ) похибки оптимального прогнозованого (екстрапольованого) значення випадкового нестаціонарного сигналу на тлі завад. Конкретизація постановки задачі оптимальної екстраполяції випадкового нестаціонарного сигналу (ВНС) на тлі завади має наступний вигляд. Вводять такі основні позначення: X(t) - випадковий нестаціонарний сигнал, значення якого прогнозуються; (t) - випадкова завада, що спотворює дані спостережень; Y(t) - випадковий сигнал, реалізація якого спостерігається, ti, i=1,n - і-й момент спостереження, Y(ti)=Yi - і- e значення Y(t) в момент часу спостереження ti, Yn+1-Y(tn+1) - значення Y(t), що прогнозується (екстраполюється), T=tn-t1 - інтервал спостереження, =tn+1-tn - інтервал екстраполяції (прогнозу), 55212 6 M[Y(t)]=m(t) - математичне сподівання Y(t), D[Y(t)=M[Y(t)-m(t)]2 - дисперсія Y(t), k(ti, tj)=M{[Y(ti)-m(ti)][Y(tj)-m(tj)]} - кореляційна функція Y(t), k (ti, tj)=M{[ (ti)-m ][ (tj)-m ]} - кореляційна функція завади (t), M[ (t)]=m (t) - математичне сподівання завади (t). На Фіг.1 показані всі основні характеристики і параметри екстраполяції ВНС. Неважко помітити різницю Xn+1 від Yn+1, та вплив завади (t) на характеристики Yn+1. Для спрощення на Фіг.1 показано два спостереження (n=2), в результаті спостереження отримують значення Y1,Y2 замість істинних значень X1,X2, по яких необхідно визначити X3, але насправді оптимально спрогнозувати значення Y3. Задача екстраполяції полягає в тому, щоб у найкращий спосіб по значенням Y1,Y2, що екстраполюються, отримати оцінку Y*3 майбутнього значення Y3. З постановки задачі зрозуміло, що найкраща екстраполяція включає не тільки прогнозування Y3, а й зменшення похибки спостережень =Y3*-X3. Для коректної постановки задачі введено такі припущення: 1. Сигнал, що спостерігають, розглядається як "адитивна суміш" сигналу Y(t) і завади (t) [5] (1) Yt Xt t , 2. Оцінку Y3* істинного значення X3 в момент часу t3 розглядають як лінійну комбінацію (функцію) попередніх значень, що спостерігають 1Y1 2 Y2 , 3. Вважають, що параметри няють вимозі нормування 1 2 1, тоді 1= , 2=1- , а оцінка (2) Y3 1, 2 задоволь(3) (4) Y2 Y1 Y2 , Оцінка Y3* по формулі (4) має наглядне фізичне пояснення: Y2 - опорне значення, (Y1-Y2) - "добавка", яка є добутком різниці Y12=Y1-Y2 значень сигналу на інтервалі спостереження та параметру екстраполяції . 4. Припускають, що завада (t) являє собою випадковий стаціонарний гаусівський сигнал з характеристиками M t m 0,M t1 , t 2 k t , (5) Y3 де k ( t) - кореляційна функція завади, що визначається за формулою 2r t , (6) k t де дисперсія (потужність) завади 2 D t , r ( t) - нормована кореляційна функція завади, інтервал часу t=t2-t1. 5. Припускають, що математична модель X(t) має вигляд : q Xt (7) it i i 0 , де q=1, детерміновані параметри задання неліній 7 55212 сторі: ності і нестаціонарності сигналу 0, 1 задовольняють умовам: 0 0 1,0 1 2, а коефіцієнти a0,a1 являють собою випадкові незалежні величини, що мають гаусівські розподіли з такими, відповідно, математичними сподіваннями і дисперсіями: 2 ;M a 2 , (8) M a0 m0 ;D a0 1 m1;D a1 0 1 6. Для визначеності припускають, що 0=0, а 1= =1/2, тоді числові характеристики ВНП приймають такий конкретний вигляд : MX t DXt 2 D (10) k X ti, t j m tj (11) 2 2 tt , i j 0 1 де через ti,tj позначені i-ий та j-ий моменти спостережень, 7. Враховують те, що ВНС та завада є незалежними сигналами, тоді M X ti m ti tj m 0, (12) Якщо характеристики ВНС (9-11) та завади (6) відомі, припущення (1) - (7) виконуються, коректно ставлять задачу оптимізації оцінки (4) значення X(t) в наступний момент часу tn+1. шляхом оптимального вибору параметру оптимізації по відповідному критерію оптимізації. Таким чином, для оптимізації оцінки Y3* необхідно вибрати критерій оптимізації та використати як керовану змінну оптимізації. Найбільш розповсюдженим і відповідаючим змісту цієї задачі є метод максимальної правдоподібності [5], який при обраних вхідних даних приводить до використання середньоквадратичного критерію методу найменших квадратів у вигляді квадрату відстані між Y3 та Y3* в евклідовому про m Y2 m Y1 m Y2 opt mY 2 M Yi 1 opt min opt m Y1 m2 Y 2 Y3 3 1 opt m Y2 2 2 opt m Y1 m Y3 2 opt 2 Y1 2 (13) (16) m1t , i 2t 2 i i 2 Yi 2 0 M Yi Yj rij mim j m2 i 2, Y M Y2 i 2 Yi (17) k Y ti, t j , (18) (19) 2t 2 i i 2 0 2, 2, (20) 2 2 tt 2r t t , (21) i j 0 1 i j З урахуванням (16-21) в кінцевому результаті для opt отримують: k y ti, t j k Y t1, t 3 k Y t1, t 2 k Y t 2, t 3 , (22) 2 Y1 При оптимальному значенні параметра екстраполяції opt дисперсія похибки екстраполяції D m0 D Y ti 2 Y2 mY 2 , Y3 При обчисленні математичних очікувань в формулі (15) враховують наступні співвідношення для характеристик випадкових процесів: 2 Y2 m Y3 M Y3 За змістом критерій (13) є дисперсією похибки екстраполяції : (14) D M Y3 Y2 Y1 Y2 2 , Для розв'язання задачі оптимізації використовують класичний метод знаходження мінімуму функції однієї змінної. Беруть похідну від D по , та прирівнюють її нулю, враховують те, що друга похідна більша нуля, вирішують отримане рівняння відносно , отримують : M Y2 Y2 Y1 M Y3 Y2 Y1 , opt (15) M Y2 Y1 2 (9) m1 t m t , 2 2t 2t , 0 1 M X ti m ti X t j m0 8 2k Y t1, t 2 приймає мінімальне значення, яке визначають за наступною формулою непрямих вимірювань: k Y t1, t 3 opt На Фіг.2 показана залежність D ( ) для одного з експериментів. Оптимальне рішення існує не при всіх початкових даних, тому треба уважно підходити до їх визначення. Структура формули (23) стає вельми наглядною, якщо її представити у вигляді: D opt M Y32 2M Y3Y3 M Y3 2 (24) min , Якщо кореляція Y3 та Y3* є повною, тоді D ( opt)min=0, тому що 1 opt 1 opt k Y t1, t 2 M Y32 m Y2 m Y3 1 M Y3 2 opt k Y t 2, t3 2 2 Y2 2M Y3 Y3 (23) , 2M Y32 (25) , Дисперсію оцінки Y3* отримують за формулою непрямих вимірів (4) 2 2 2 2 D Y3 1 opt opt Y1 Y2 (26) 2 opt 1 k Y t1, t 2 , opt Оцінку Y3* отримують у вигляді зваженої суми значень Y1,Y2, що спостерігаються, з оптимальними ваговими коефіцієнтами opt та (1- opt), тому дисперсія оптимальної оцінки 9 * D Y3 D Y3 , 55212 (27) Нерівність (27) показує, що оптимальна екстраполяція дає меншу дисперсію оптимальної оцінки, ніж дисперсія очікуваного значення, що спостерігається. Цей висновок дуже важливий для практичних застосувань. З нього випливає, що оптимальна екстраполяція, якщо вона можлива, є дуже корисною тому, що суттєво підвищує точність оцінювання значень ВНС. Ефективність оптимального способу екстраполяції пропонують оцінювати за наступними формулами непрямих вимірювань системи оцінювання ефективності екстраполяції. Відношення сигнал/шум на виході оптимального екстраполятора: D Y3 , h1 (28) D opt min де D[Y3] - дисперсія випадкового сигналу, що буде спостерігатися у момент часу t3, D ( opt)min - мінімальна дисперсія похибки екстраполяції. Відношення дисперсії випадкового сигналу, що буде спостерігатися у момент часу t3, до дисперсії екстрапольованого значення сигналу D[Y3*] D Y3 , h2 (29) D Y3 Відношення різниці між дисперсією випадкового сигналу, що буде спостерігатися у момент часу t3, та дисперсією екстрапольованого сигналу D[Y3*] до мінімальної дисперсії похибки екстраполяції : D Y3 D Y3 (30) , opt min Для оцінки середньої величини похибки екстраполяції використовують абсолютну похибку h3 D (31) m m3 m3 , та відносну похибку m , (32) m m3 На Фіг.3 показана узагальнена структурна схема способу. Спосіб реалізується наступним чином. Цикл вимірювань починають з того, що з об'єкту вимірювання ОВ (блок 1) за сигналами керування СУ блока 2 керування та синхронізації БУС у моменти часу t1,t2 вимірюють значення випадкових нестаціонарних сигналів Y1,Y2 (блок 4), що спостерігаються, і подають на блок обчислення БО (блок 5). Крім того, на БО з бази даних також подають апріорно відомі параметри сигналу і завади: m0 ,m1, 2 , 2 , 2 , , 0 1 де m0,m1 - математичні сподівання параметрів a0,a1; 2, 2 - середні квадратичні відхилення парамет0 1 рів a0,a1; 2 - середнє квадратичне відхилення завади, 10 - інтервал кореляції завади. За наступною командою БУС БО виконує обчислення за формулами непрямих вимірювань (9) - (11), (16), (17), (20) - (23), (26), (28) - (30), що в даному випадку відіграють роль операторних рівнянь роботи певних функціональних пристроїв оптимального екстраполятора. Після закінчення обчислень БО за останньою командою БУС подає результати обчислень у вигляді параметрів opt,D ( opt)min,D[y3*],h1,h2,h3,Y3*,Y3 на блок 6 - блок відображення результатів БВР у даному циклі. Одночасно з відображенням результатів екстраполяції ці параметри запам'ятовують в базі даних (блок 3), для того, щоб після декількох циклів можна було б побудувати графіки зміни цих параметрів. Як випливає з принципу роботи структурної схеми способу, вхідні сигнали Y1,Y2,t1,t2,t3, , 2 , 2 , 2 , згідно операторних рівнянь (9)m0,m1, 0 1 (11), (16)-(17), (20)-(23), (26)-(30) перетворюють у вихідні сигнали Y3,Y3*, opt, D[Y3*],D ( opt)min,h1,h2,h3. Тому цей спосіб названо способом оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад, він дозволяє оптимально обчислювати параметр opt, екстраполювати значення Y3* з дисперсіями D[y3*] D[Y3] i D ( opt)min. Приклад 1. В цьому прикладі наведені результати експерименту, що був проведений методом цифрового статистичного імітаційного моделювання способу. Виконують оптимальну екстраполяцію значення Y3* по двох попередніх значеннях Y1,Y2. Результати вимірювання X1,X2,X3,Y1,Y2,Y3, моделюють реалізаціями випадкових величин за допомогою функції (33) системи MathCAD Yi rnorm n, M Y , , (33) i 1,3 де число n реалізацій для кожної точки вибрано n=1,M[Yi] - математичне очікування ВНС, а - середньоквадратичне відхилення спостерігаємого ВНС, яке обчислюються за формулою (17). Для моделювання роботи структурної схеми способу була розроблена програма на мові системи MathCAD. Вона дозволяє використовувати різні вхідні дані експериментів і виконувати статистичні експерименти. В експерименті були обрані наступні початкові дані : t1=6c; t2=10c; t3=12c, де t1,t2 - моменти часу, в які спостерігаються реалізації Y1,Y2 випадкового нестаціонарного сигналу (ВНС), t3 - момент часу, для якого виконується екстраполяція, =0,5c - інтервал кореляції завади, =0,01 B, m0=1 B, m1=0,1B/c, 0=0,1 B, 1=0,01 B. Реалізації Yi утворюють за допомогою функції генерації випадкових чисел (33) з гаусівським розподілом при заданих n,M[Yi], . В експерименті задана точність моделювання "шість знаків після коми". Наприклад, в результаті однократного використання операції (33) були отримані такі реалізації вимірювань: Y1=1,030483, Y2=1,029272, 11 55212 Y3=1,016351. В таблиці показано результати в одному конкретному експерименті, а на Фіг.4 відображені графіки X(t), Y(t) та Z(t), де Z(t) відображає Y3* на 12 графіку. На Фіг.2 відображений графік D ( )=f( для різних значень . opt) Таблиця Результати експерименту X1 1,015018 X2 1,024681 Y3* 1,028786 -0,401238 h2 0,994706 0,015465 D ( )2 0,000121 -0,4 opt 1 2 X3 Y1 1,028772 1,030483 Продовження табл. D[Y3] D[Y3*] 0,0113 0,01136 Продовження табл. 2 3 0,004591 -0,01242 Продовження табл. D ( )3 3 0,000837 -0,8 Аналіз результатів експерименту показує працездатність і високу ефективність способу за Фіг.3 навіть при низькому відношенню середньоквадратичних значень сигнал/шум: приблизно 3-4. За результатами експерименту можна зробити такі висновки: 1. Показник ефективності оптимальної екстраполяції h1, показує, що оптимальна екстраполяція забезпечує достатньо високу точність - дисперсія похибки (шумів) екстраполяції в 56 разів менше дисперсії самого ВНС. 2. В результаті оптимальної екстраполяції значення Y3* для моменту часу t3=12c знаходиться ближче до X3 ніж Y3 (дивись графік Фіг.4); дисперсія D[Y3*] оптимально екстрапольованого значення приблизно у h2=0,99 разів більше, ніж дисперсія D[Y3] значення сигналу, що буде спостерігатися в t3 . 3. Показник ефективності оптимальної екстраполяції h3 показує, що оптимальна екстраполяція забезпечує різницю між дисперсією D[Y3] і дисперсією оптимальної оцінки D[Y3*] вдвічі меншу дисперсії D ( opt)min похибки екстраполяції. 4. Графік Фіг.2 показує, що дисперсія D ( opt) має мінімум при значенні opt. Y2 1,029272 Y3 1,016351 D ( opt)min 0,0002 h1 56,49051 D ( )1 0,001047 0 D ( )4 0,001811 -1 1 4 Тому, якщо є можливість отримати необхідні вихідні дані, завжди корисно проводити оптимальну екстраполяцію. Наведені результати експерименту наглядно ілюструють новизну, корисність та високу ефективність способу, що пропонуються. Джерела інформації: 1. United States Patent № 4,635,182. Kenneth J. Hintz. Apparatus for controlling multiple time-varying processes. Jan. 6, 1987. 2. United States Patent № 5,717,789. Image enhaancement by non-linear extrapolation in frequency space. Inventoes: Charles H. Anderson, Hayik R. Greenspan, California. Institute bjf Technology. Pasadena. Feb. 10, 1998. 3. United States Patent № 6,505,053 B1, Method for sinusoidal modeling and predicthion of fast-fading processes. Inventoes: Jack Harriman Winters, JengKuang Hwang. New York. Jan. 7, 2003. 4. Дьяконов В. П. Энциклопедия MathCAD 2001 и MathCAD 11. - M: Изд. Солон-пресс, 2004. 832с. 5. Игнатов В. А. Теория информации и передачи сигналов. Учебник для вузов. 2-ое изд. Перераб. и доп. - М.: Радио и связь, 1990. - 280с. 13 55212 14 15 Комп’ютерна верстка Л. Ціхановська 55212 Підписне 16 Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for optimal extrapolation of random non-stationary signals at background of noise
Автори англійськоюHuzii Mykola Mykolaiovych, Ihnatov Volodymyr Oleksiiovych, Andreiev Oleksandr Volodymyrovych, Andreev Volodymyr Illich
Назва патенту російськоюСпособ оптимальной экстраполяции случайных нестационарных сигналов на фоне помех
Автори російськоюГузий Николай Николаевич, Игнатов Владимир Алексеевич, Андреев Александр Владимирович, Андреев Владимир Ильич
МПК / Мітки
МПК: G06C 17/00, G01S 7/36
Мітки: випадкових, нестаціонарних, спосіб, сигналів, оптимальної, тлі, завад, екстраполяції
Код посилання
<a href="https://ua.patents.su/8-55212-sposib-optimalno-ekstrapolyaci-vipadkovikh-nestacionarnikh-signaliv-na-tli-zavad.html" target="_blank" rel="follow" title="База патентів України">Спосіб оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад</a>
Попередній патент: Конвеєрний криптографічний обчислювач
Наступний патент: Конвеєрний криптографічний обчислювач
Випадковий патент: Спосіб футерування барабанного млина












