Спосіб двопараметричної оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад
Номер патенту: 62878
Опубліковано: 26.09.2011
Автори: Андреєв Володимир Ілліч, Андреєв Олександр Володимирович, Жуков Ігор Анатолійович, Ігнатов Володимир Олексійович
Формула / Реферат
1. Спосіб двопараметричної оптимальної екстраполяції нестаціонарних випадкових сигналів на тлі завад, у якому для оптимальної екстраполяції нестаціонарного випадкового сигналу на тлі завади використовують метод максимальної правдоподібності, а також декілька попередніх результатів вимірювань зашумленого сигналу з апріорно відомими ймовірнісними характеристиками (математичні очікування, дисперсії, кореляційні функції сигналу та завади), який відрізняється тим, що в основу способу покладено задачу визначення оптимального прогнозованого (екстрапольованого) значення випадкового нестаціонарного сигналу на тлі завад за критерієм мінімуму дисперсії похибки екстраполяції.
2. Спосіб за п. 1, який відрізняється тим, що оптимальна оцінка ![]() для майбутнього моменту часу
для майбутнього моменту часу ![]() екстрапольованого значення випадкового нестаціонарного сигналу
екстрапольованого значення випадкового нестаціонарного сигналу
![]() , (1)
, (1)
що спостерігають на тлі завади ![]() у два попередні моменти часу
у два попередні моменти часу ![]() ,
, ![]() у вигляді зашумленого сигналу
у вигляді зашумленого сигналу
![]() , (2)
, (2)
де q=1, детерміновані параметри ![]() ,
, ![]() задання нелінійності і нестаціонарності випадкового сигналу
задання нелінійності і нестаціонарності випадкового сигналу ![]() задовольняють умовам:
задовольняють умовам:
![]() ,
, ![]() , (3)
, (3)
коефіцієнти ![]() ,
, ![]() є випадковими незалежними величинами, що мають гауссівські розподіли з математичними очікуваннями і дисперсіями:
є випадковими незалежними величинами, що мають гауссівські розподіли з математичними очікуваннями і дисперсіями:
![]() ;
; ![]() ;
; ![]() ;
; ![]() , (4)
, (4)
заваду (шум) ![]() представляють як випадковий стаціонарний гауссівський сигнал з характеристиками
представляють як випадковий стаціонарний гауссівський сигнал з характеристиками
![]() ,
, ![]() , (5)
, (5)
визначають за двома попередніми вимірюваннями ![]() та
та ![]() і апріорною інформацією (1)-(5) за формулою непрямих вимірювань:
і апріорною інформацією (1)-(5) за формулою непрямих вимірювань:
![]() , (6)
, (6)
де значення параметрів ![]() ,
, ![]() вибирають оптимальним способом розв'язання задачі оптимізації з використанням класичного методу знаходження мінімуму дисперсії похибки екстраполяції як функції двох змінних:
вибирають оптимальним способом розв'язання задачі оптимізації з використанням класичного методу знаходження мінімуму дисперсії похибки екстраполяції як функції двох змінних:
![]() (7)
(7)
беруть перші похідні від ![]() по
по ![]() ,
, ![]() та прирівнюють їх до нуля:
та прирівнюють їх до нуля:
![]() ;
; ![]() ; (8)
; (8)
враховують те, що детермінант матриці з других похідних ![]() , тобто
, тобто
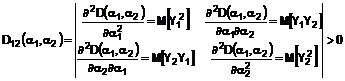 , (9)
, (9)
а також те, що друга похідна
![]() , (10)
, (10)
в нашому випадку
![]() ,
,
![]() , (11)
, (11)
тому
![]()
![]()
і має місце мінімум ![]() ,
,
далі розв'язують систему рівнянь другого порядку відносно ![]() ,
, ![]() , отримують
, отримують ![]() ,
, ![]() екстрапольованого значення
екстрапольованого значення ![]() за формулою непрямих вимірювань:
за формулою непрямих вимірювань:
![]() ; (12)
; (12)
![]() ; (13)
; (13)
де
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() - математичні сподівання сигналів
- математичні сподівання сигналів ![]() , що спостерігають в моменти часу
, що спостерігають в моменти часу ![]() , що обчислюють при
, що обчислюють при ![]() ,
, ![]() за формулою непрямих вимірювань:
за формулою непрямих вимірювань:
![]() , (14)
, (14)
де ![]() ,
, ![]() - математичні сподівання випадкових параметрів
- математичні сподівання випадкових параметрів ![]() ,
, ![]() ,
,
![]() - параметр нелінійності випадкового сигналу, що спостерігається (НВС),
- параметр нелінійності випадкового сигналу, що спостерігається (НВС),
![]() - дисперсія випадкового нестаціонарного сигналу
- дисперсія випадкового нестаціонарного сигналу ![]() в
в ![]() -ті моменти часу,
-ті моменти часу,
![]() - кореляційна функція ВНС
- кореляційна функція ВНС ![]() для
для ![]() -го та
-го та ![]() -го моментів спостереження;
-го моментів спостереження;
![]() ,
, ![]() забезпечують мінімальне значення дисперсії похибки оптимальної екстраполяції, яку розраховують за формулою непрямих вимірювань:
забезпечують мінімальне значення дисперсії похибки оптимальної екстраполяції, яку розраховують за формулою непрямих вимірювань:
![]() (15)
(15)
3. Спосіб за п. 1, який відрізняється тим, що дисперсію оптимальної оцінки ![]() отримують за формулою непрямих вимірювань:
отримують за формулою непрямих вимірювань:
![]() (16)
(16)
4. Спосіб за п. 1, який відрізняється тим, що ефективність оптимального способу екстраполяції оцінюють за формулами непрямих вимірювань: відношенням сигнал/шум на виході оптимального екстраполятора
![]() , (17)
, (17)
де ![]() - дисперсія значення випадкового сигналу, що буде спостерігатися у момент часу
- дисперсія значення випадкового сигналу, що буде спостерігатися у момент часу ![]() ,
,
![]() - мінімальна дисперсія похибки екстраполяції,
- мінімальна дисперсія похибки екстраполяції,
відношенням дисперсії випадкового сигналу, що буде спостерігатися у момент часу ![]() , до дисперсії екстрапольованого оптимального значення сигналу
, до дисперсії екстрапольованого оптимального значення сигналу ![]() :
:
![]() , (18)
, (18)
відношенням різниці між дисперсією випадкового сигналу, що спостерігається у момент часу ![]() , та дисперсією екстрапольованого сигналу
, та дисперсією екстрапольованого сигналу ![]() до мінімальної дисперсії похибки екстраполяції
до мінімальної дисперсії похибки екстраполяції
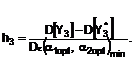 (19)
(19)
Текст
1. Спосіб двопараметричної оптимальної екстраполяції нестаціонарних випадкових сигналів на тлі завад, у якому для оптимальної екстраполяції нестаціонарного випадкового сигналу на тлі завади використовують метод максимальної правдоподібності, а також декілька попередніх результатів вимірювань зашумленого сигналу з апріорно відомими ймовірнісними характеристиками (математичні очікування, дисперсії, кореляційні функції сигналу та завади), який відрізняється тим, що в основу способу покладено задачу визначення оптимального прогнозованого (екстрапольованого) значення випадкового нестаціонарного сигналу на тлі завад за критерієм мінімуму дисперсії похибки екстраполяції. 2. Спосіб за п. 1, який відрізняється тим, що оп 0 0 1 , 0 2 2 , (3) коефіцієнти a 0 , a1 є випадковими незалежними величинами, що мають гауссівські розподіли з математичними очікуваннями і дисперсіями: 2 2 Ma0 m0 ; Da 0 0 ; Ma1 m1 ; Da1 1 , (4) заваду (шум) t представляють як випадковий стаціонарний гауссівський сигнал з характеристиками Mt m 0 , Mt1 , t 2 k t , (5) q i t i , (1) i0 що спостерігають на тлі завади t у два попере враховують те, що детермінант матриці з других похідних D12 1, 2 0 , тобто D12 1, 2 2 M Y1 2 1 D1, 2 MY2 Y1 2 1 2 (13) (19) дні моменти часу t1 , t 2 у вигляді зашумленого сигналу Yt Xt t , (2) 2D1, 2 беруть перші похідні від D по 1 , 2 та прирівнюють їх до нуля: D D 0; 0 ; (8) 1 2 62878 Dε α1, α2 M Y3 α1Y1 α 2 Y2 2 ; (7) часу t 3 екстрапольованого значення випадкового нестаціонарного сигналу (11) де значення параметрів 1 , 2 вибирають оптимальним способом розв'язання задачі оптимізації з використанням класичного методу знаходження мінімуму дисперсії похибки екстраполяції як функції двох змінних: UA * Y3 1Y1 2 Y2 , (6) * тимальна оцінка Y3 для майбутнього моменту Xt U визначають за двома попередніми вимірюваннями Y1 Yt1 та Y2 Yt 2 і апріорною інформацією (1)-(5) за формулою непрямих вимірювань: 2D1, 2 MY1Y2 1 2 2D1, 2 2 2 2 M Y2 0 , (9) 3 62878 а також те, що друга похідна 2D1, 2 2 1 4 в нашому випадку 2D1, 2 0 , (10) 2 M Y1 m2 D Y1 0 , Y 2 1 1 2D1, 2 2D1, 2 2 2 MY2 Y1MY1Y2 M Y1 M Y2 , (11) 21 1 2 тому mYi - математичні сподівання сигналів Yi , що 2 D12 1, 2 0, M Y1 0, спостерігають в моменти часу t i , що обчислюють і має місце мінімум D 1, 2 , далі розв'язують систему рівнянь другого порядку відносно 1 , 2 , отримують 1opt , 2opt екстра при 0 0 , 1 за формулою непрямих вимірювань: m Yi m 0 m1t i , (14) * польованого значення Y3 за формулою непрямих вимірювань: b a b 2a12 1opt 1 22 ; (12) a11a 22 a 21a12 2opt де m0 , m1 - математичні сподівання випадкових параметрів a 0 , a1 , - параметр нелінійності випадкового сигналу, що спостерігається (НВС), D Yi - дисперсія випадкового нестаціонарного сиг a11b 2 b1a 21 ; (13) a11a 22 a 21a12 де налу Y в i -ті моменти часу, k t i , t j - кореляційна функція ВНС Yt для i -го та a12 m Y1 m Y2 kt1, t 2 ; a11 m2 DY1 ; Y 1 j -го моментів спостереження; b1 m Y1 m Y3 k t1, t 3 ; 1opt , 2opt забезпечують мінімальне значення a21 mY1 mY2 kt1, t 2 ; дисперсії похибки оптимальної екстраполяції, яку розраховують за формулою непрямих вимірювань: a22 m2 DY2 ; Y 2 b2 m Y2 m Y3 k t 2 , t 3 ; D 1opt , 2opt min m2 Y 3 2 2 1opt m2 2 2opt m2 2 21opt mY1 mY3 kt1, t 3 2 Y Y Y Y Y 3 1 1 2 22opt mY2 mY3 kt 2, t 3 21opt 2opt mY1 mY2 kt1, t 2 . 2 (15) * 3. Спосіб за п. 1, який відрізняється тим, що дисперсію оптимальної оцінки Y3 отримують за формулою непрямих вимірювань: * 2 2 D Y3 1opt D Y1 1opt D Y2 21opt 2opt k Y t1, t 2 . (16) 4. Спосіб за п. 1, який відрізняється тим, що ефективність оптимального способу екстраполяції оцінюють за формулами непрямих вимірювань: відношенням сигнал/шум на виході оптимального екстраполятора DY3 , (17) h1 D 1opt , 2opt сії екстрапольованого оптимального значення сиг лу, що буде спостерігатися у момент часу t 3 , * дисперсію екстрапольованого сигналу D Y3 мінімальної дисперсії похибки екстраполяції min де DY3 - дисперсія значення випадкового сигна D 1, 2 - мінімальна дисперсія похибки екстраполяції, відношенням дисперсії випадкового сигналу, що буде спостерігатися у момент часу t 3 , до диспер * налу D Y3 : h2 DY3 , (18) * D Y3 відношенням різниці між дисперсією випадкового сигналу, що спостерігається у момент часу t 3 , та h3 * DY3 D Y3 D 1opt , 2opt min . (19) до 5 Корисна модель належить до теорії випадкових процесів та використання цієї теорії для розв'язання прикладних задач надійності, діагностування, контролю якості, обробки сигналів на тлі завад, контролю працездатності та прогнозуванні трафіку обчислювальних мереж, при макропрогнозуванні трендів в економіці при малих обсягах виборок в часових рядах. Аналогом запропонованого способу є винахід, який відноситься до способів управління декількома випадковими нестаціонарними процесами за допомогою адаптивної оцінки і збору інформації [1]. Більш конкретно, цей винахід стосується адаптивного пристрою контролю, в якому моніторинг минулих станів процесів використовується для екстраполяції поточного стану кожного процесу, що контролюється, а також для оцінки факторів невизначеності в кожному процесі. Недоліком є те, що не враховується дія завади. Аналогом запропонованого способу є також спосіб покращення зображення нелінійною екстраполяцією в частотному просторі [2]. У ньому вхідне зображення збільшується для того, щоб включити просторові частотні вузли, які мають частоти вищі ніж ті, що входять у вхідне зображення. Карта перетинів будується на основі вхідного зображення з використанням високоякісної прохідної фільтрувальної техніки. Збільшена карта створюється за допомогою використання нелінійного оператора до карти перетинів із збереженням фазових переходів перетинів вхідного зображення. Збільшена карта додається до вхідного зображення, щоб отримати результуюче зображення, яке має просторові частоти, більші ніж у вхідному зображенні. Простота обчислень і легкість реалізації дозволяють отримати покращене зображення в реальному часі для таких додатків як відеофони, покращення телевізійного зображення, реставрація старих фільмів. Недоліком способу є те, що в описі патенту не показано, як працює запропонований спосіб при впливі на зображення випадкової завади. Крім того, цей спосіб вимагає відносно великих обсягів спостережень для отримання спектру. Аналогом запропонованого способу є також метод синусоїдального моделювання та прогнозу швидко замираючих процесів при федінгу радіосигналів [3]. Пропонується метод прогнозування швидко замираючих процесів з використанням синусоїдальних методів моделювання. В методі спочатку використовується низькочастотна фільтрація поступаючого сигналу, що збільшує потужність зникаючого сигналу до потужності шуму. Використовується частотна оцінка основної гармоніки і розробляється синусоїдальна модель зникаючого процесу. Ця модель використовується для покращення характеристик часових схем обробки і зменшення ефекту зникнення. Недоліком є те, що не мінімізується дисперсія похибки прогнозування сигналу. Прототипом способу двопараметричної оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад є спосіб оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі 62878 6 завад [4], який дозволяє по двом точкам для процесу, що спостерігається, Y1, Y2 отримати оцінку Y*3 для третьої точки Y3, крім того, цей спосіб дозволяє обчислити наступні параметри процесу екстраполяції: Dε(opt)min - мінімальну похибку екстраполяції, дисперсію оцінки D[Y*3], h1 - коефіцієнт відношення сигнал/шум на виході оптимального екстраполятора. Недоліком патенту є те, що при обчисленні параметру оптимальної екстраполяції opt він може бути негативним opt0 порушуються, а це може привести до спотворення результатів екстраполяції. Запропонований спосіб двопараметричної оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад не має цих недоліків, крім того він дає більш високу точність екстраполяції і більший коефіцієнт h1 - відношення сигнал/шум на виході екстраполятора. В основу корисної моделі покладено задачу визначення оптимізуючи параметрів 1opt, 2opt, за допомогою яких визначають оптимальне прогнозне (екстрапольоване) значення випадкового нестаціонарного сигналу Y*3 на тлі завад по двом попереднім значенням сигналу Y1, Y2, що спостерігаються, за критерієм мінімуму дисперсії похибки екстраполяції. Конкретизацію постановки задачі оптимальної екстраполяції випадкового нестаціонарного сигналу (ВНС) на тлі завади виконано наступним чином. Введено такі основні позначення: Х(t) - випадковий нестаціонарний сигнал, значення якого прогнозуються; ξ(t) - випадкова завада, що спотворює дані спостережень; Y(t) - випадковий сигнал, реалізація якого спостерігається, ti, і=n, n - і-й момент спостереження, Y(ti)=Yi - і-e значення Y(t) в момент часу спостереження ti, Yn+1=Y(tn+1) - значення Y(t), що прогнозується (екстраполюється), Т=tn-t1 - інтервал спостереження, =tn+1-tn - інтервал екстраполяції (прогнозу), М[Y(t)]=m(t) - математичне сподівання Y(t), 2 D[Y(t)]=M[Y(t)-m(t)] - дисперсія Y(t), k(ti, tj)=M{[Y(ti)-m(ti)][Y(tj)-m(tj)]} - кореляційна функція Y(t), kξ(ti, tj)=M{[ξ(ti)-mξ][ξ(tj)-mξ) - кореляційна функція завади ξ(t), М[ξ(t)]=mξ(t) - математичне сподівання завади ξ(t). На Фіг.1 показані всі основні характеристики і параметри екстраполяції НВС. Неважко помітити різницю Хn+1 від Yn+1, та вплив завади ξ(t) на характеристики Yn+1. Для спрощення на Фіг.1 показано два спостереження (n=2), в результаті спостереження отримують значення Y1, Y2 замість істинних значень X1, Х2, по яким необхідно визначити Х3, але насправді оптимально спрогнозувати значення Y3. Задача екстраполяції полягає в тому, щоб у найкращий спосіб по значенням Y1, Y2, що екстраполюються, отримати оцінку Y*3 майбутнього значення Y3. З постановки задачі зрозуміло, що най 7 62878 краща екстраполяція включає не тільки прогнозування Y3, а й зменшення похибки спостережень ε=Y*3-X3. Для коректної постановки задачі вводять такі припущення: 1. Сигнал, що спостерігають, розглядається як «адитивна суміш» сигналу Y(t) і завади ξ(t) [6] Y(t)=X(t)+ξ(t); (1) 2. Оцінку Y3* істинного значення Х3 в момент часу t3 розглядають як лінійну комбінацію (функцію) попередніх значень, що спостерігають: Y*3=1Y1+2Y2; (2) 3. Припускають, що завада ξ(t) являє собою випадковий стаціонарний гауссівський сигнал з характеристиками M[ξ(t)]=mξ=0, M[ξ(t1), ξ(t2)]=kξ(Δt), (3) де kξ(Δt) - кореляційна функція завади, яку визначають за формулою k t 2r t , (4) 2 де дисперсія (потужність) 8 rξ(Δt) - нормована кореляційна функція завади, Δt - інтервал часу Δt=t2-t1. 4. Припускають, що математична модель X(t) має вигляд: Xt q i t i , (5) i0 де q=1, детерміновані параметри задання нелінійності і нестаціонарності сигналу 0, 1 задовольняють умовам: 0≤0≤1, 0≤1≤2, а коефіцієнти а0, а1 являють собою випадкові незалежні величини, що мають гауссівські розподіли з такими, відповідно, математичними сподіваннями і дисперсіями: 2 2 М(а0)=m0; Da 0 0 ; М(а1)=m1; Da1 1 . (6) 5. Для визначеності припускають, що 0=0, а 1==1/2, тоді числові характеристики НВС приймають такий конкретний вигляд: M[X(t)]=m0+m1t=m(t); (7) 2 2 DXt 0 1 t 2 ; (8) завади 2 Dt , 2 2 0 1 tit j , (9) k X t i , t j M Xt i mt i X t j m t j де через ti, tj позначені i-ий та j-ий моменти спостережень. Враховують те, що НВС та завада є незалежними, тому M{[Х(ti)m(ti)][ξ(tj)-mξ]}=0. (10) Якщо характеристики НВС (7)-(9) та завади (4) відомі, припущення (1)-(5) виконуються, коректно ставлять задачу оптимізації оцінки (2) значення Х(t) в наступний момент часу tn+1 шляхом оптимального вибору параметрів оптимізації 1, 2 по відповідному критерію оптимізації. Таким чином, для оптимізації оцінки Y*3 вибирають критерій оптимізації та використовують 1, 2 як керовані змінні оптимізації. Найбільш розповсюдженим і таким, що відповідає змісту цієї задачі, є метод максимальної правдоподібності [6], який при обраних вхідних даних приводить до середньоквадратичного критерію методу найменших квадратів у вигляді квадрату відстані між Y*3 та Y3 в евклідовому просторі: D(ε)=M[(Y3-Y*3]. (11) Для розв'язання задачі оптимізації враховують наступні співвідношення для характеристик випадкових сигналів, що спостерігаються: MYi m0 m1t i ; (12) 2 DYti 2 0 i2i2 2 ; (13) Y i M Yi Yj rij mim j k Y t i , t j ; (14) M Yi2 mi2 2 ; (15) Y 2 Yi 2 0 i i2i2 2 ; (16) 2r ti t j , (17) 2 2 k y t i , t j 0 1 t i t j дe r t i t j e t j ti t , (18) Δtξ - інтервал кореляції завади. З урахуванням (18) співвідношення (17) для кореляційної функції суміші НВС і завади має такий вигляд: t j ti t . (19) k y ti, t j Для розв'язання задачі оптимізації використовують класичний метод знаходження мінімуму функції двох змінних. Беруть похідні від Dε по 1, 2 та прирівнюють до нуля: D D 0; 0; 1 2 враховуючи те, що другі похідні D D 0, 0, 2 1 1 2 розв`язують систему рівнянь другого порядку відносно 1, 2, отримують оpt1, оpt2. Підставляють у вираз (11) замість Y*3 його значення (2). Тоді отримують: 2 Dε(1, 2)=M[(Y3-1Y1-2Y2) ]. (20) Беруть похідні від Dε(1, 2) по 1 та 2, і прирівнюють їх нулю: D 1, 2 M2Y3 1Y1 2 Y2 Y1 0 ; (21) 1 2 0 2 1 t i t j 2e D 1, 2 M2Y3 1Y1 2 Y2 Y2 0 . (22) 2 Використовують властивості математичного сподівання для виразів (21), (22) та перемножуючи складові у фігурних дужках, отримують: M Y Y Y Y 0 . (24) 2 M 1Y1 2 Y1Y2 Y1Y3 0 ; (23) 2 1 1 2 2 Y2 2 3 9 62878 У системі рівнянь (25) замінюючи математичні 2 M 1Y1 2 Y1Y2 MY1Y3 . (25) 2 M 1Y1Y2 2 Y2 MY2 Y3 10 2 2 сподівання M Y1 , M[Y1Y2], M[Y1Y3], M Y2 , M[Y2Y3] їх значеннями, отримують: 1 m 2 D Y 2 m Y m Y k t1, t 2 m Y m Y k t 1, t 3 Y1 1 1 2 1 3 . (26) 2 1 m Y1 m Y2 k t1, t 2 2 m Y D Y2 m Y2 m Y3 k t 2 , t 3 2 Систему рівнянь (26) записують у матричній формі: b1 1opt 1a11 2a12 b1 . (27) 1a 21 2a 22 b 2, де 1 a11 b1 m Y1 m Y3 k t1, t 3 ; 2opt a21 mY1 mY2 kt1, t 2 ; a22 m2 DY2 ; Y 2 b2 m Y2 m Y3 k t 2 , t 3 . 2 1 D12 1, 2 D m Y2 2 M Y1 Y1 m Y2 a11 a12 a 21 a 22 12 a11b 2 b1a 21 . (29) a11a 22 a 21a12 2 2D1, 2 MY2 Y1 2 1 D Y1 m2 Y2 b1a 22 b 2a12 ; (28) a11a 22 a 21a12 b1 a 21 b 2 2D1, 2 MY1Y2 1 2 2D1, 2 2 2 0 . (30) 2 M Y2 2 2 D12 1, 2 M Y1 M Y2 MY1Y2 MY2 Y1 m2 Y1 Беруть другі похідні від ∂ Dε(1, 2), отримують детермінант матриці з других похідних Розв'язують систему рівнянь (27) відносно 1 і 2 по правилу Крамера, отримують: 2D1, 2 a 22 a11 a12 a 21 a 22 12 a12 m Y1 m Y2 k t1, t 2 ; a11 m2 DY1 ; Y a12 b2 kt1, t 2 m Y2 m Y1 kt 2 , t1 0 , (31) 2 а M Y1 0 . Тому при оптимальному значенні параметрів 1оpt, 2оpt дисперсія похибки екстраполяції мінімальна та приймає таке значення: D 1opt , 2opt min m2 Y 3 2 2 1opt m2 2 2opt m2 2 21opt mY1 mY3 kt1, t 3 2 Y Y Y Y Y 3 1 1 2 2 22opt mY2 mY3 kt 2, t 3 21opt 2opt mY1 mY2 kt1, t 2 . (32) На Фіг.2 показана залежність Dε(1оpt, 2оpt) від 1 і 2. Дисперсію оцінки Y*3 отримують за наступною формулою: DY *3 D 1opt Y1 2opt Y2 D 1opt Y1 D 2opt Y2 2D 1opt Y1 2opt Y2 2 1opt 2 1 Y 2opt 2 2 2 Y 21opt 2opt k Y t1, t 2 Оцінка Y*3 отримана у вигляді суми значень Y1, Y2, що спостерігаються, з оптимальними ваговими коефіцієнтами 1оpt, 2оpt, то використовують наступну нерівність: * D[Y 3]
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for two-parameter optimum extrapolation of nonstationary random signal against the bacground of hindrances
Автори англійськоюIhnatov Volodymyr Oleksiiovych, Zhukov Ihor Anatoliiovych, Andreiev Oleksandr Volodymyrovych, Andreev Volodymyr Illich
Назва патенту російськоюСпособ двухпараметрической оптимальной экстраполяции случайных нестационарных сигналов на фоне помех
Автори російськоюИгнатов Владимир Алексеевич, Жуков Игорь Анатольевич, Андреев Александр Владимирович, Андреев Владимир Ильич
МПК / Мітки
МПК: G06C 3/00, G01S 17/00
Мітки: сигналів, випадкових, оптимальної, двопараметричної, тлі, екстраполяції, завад, спосіб, нестаціонарних
Код посилання
<a href="https://ua.patents.su/8-62878-sposib-dvoparametrichno-optimalno-ekstrapolyaci-vipadkovikh-nestacionarnikh-signaliv-na-tli-zavad.html" target="_blank" rel="follow" title="База патентів України">Спосіб двопараметричної оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад</a>
Попередній патент: Спосіб відновлення поверхні тертя в імпульсному магнітному полі за допомогою модульованого сигналу
Наступний патент: Пристрій для сортування сипучих матеріалів
Випадковий патент: Спосіб експериментального моделювання синдрому інсулінорезистентності












