Спосіб відтворення реперних точок міжнародної температурної шкали

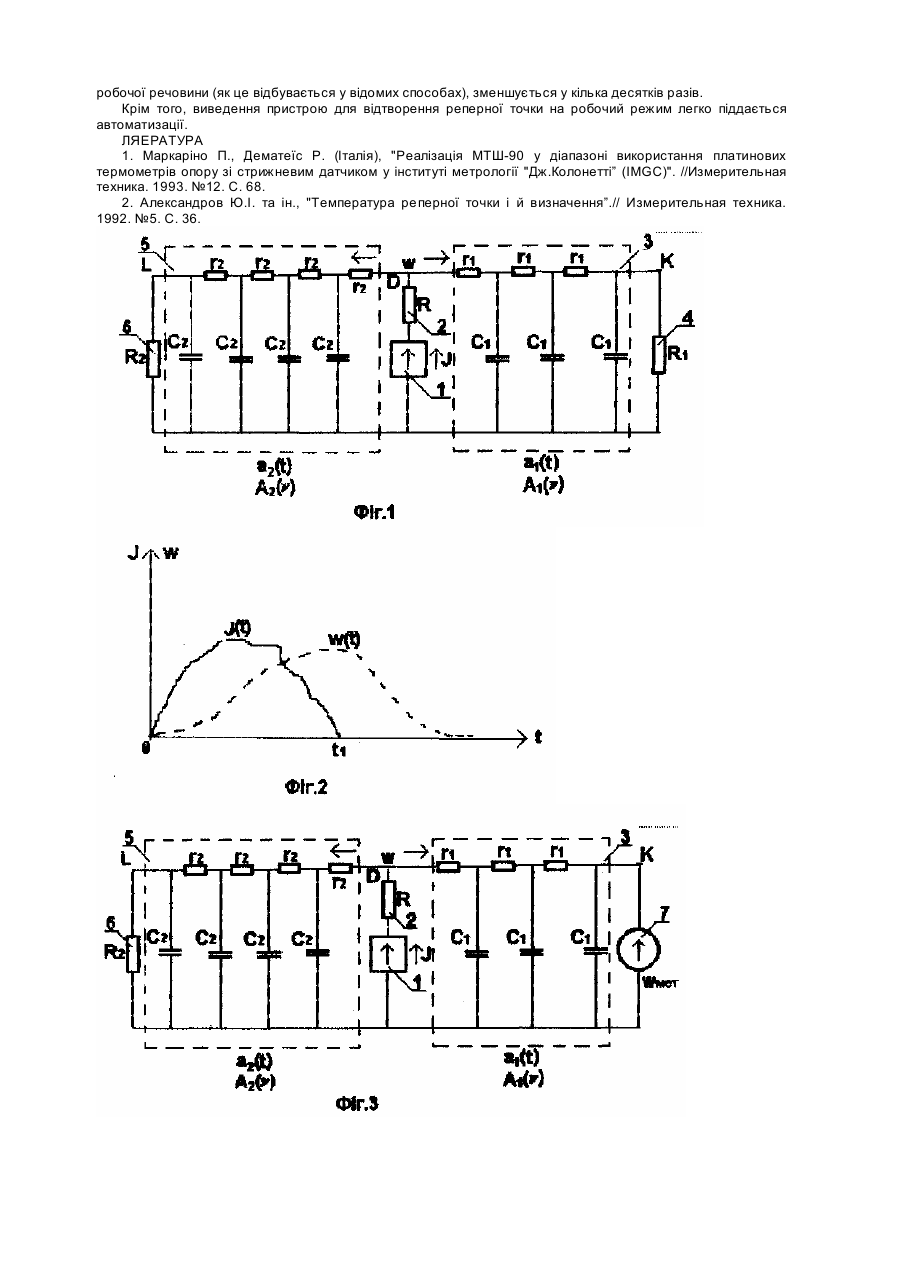
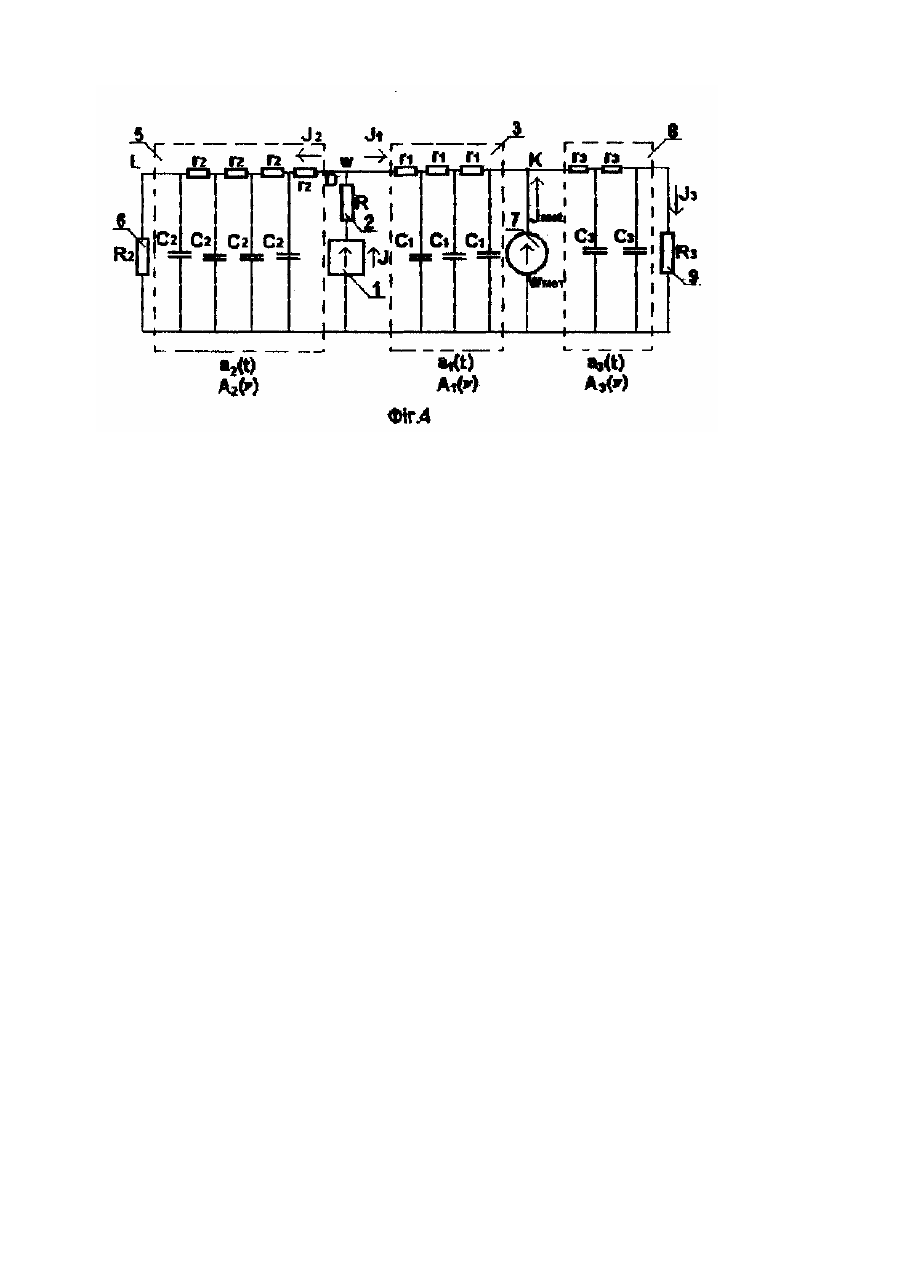
Запропонований винахід відноситься до вимірювальної техніки, а саме, для відтворення реперних точок міжнародної температурної шкали з підвищеною точністю. Пристрій, який реалізує відомий спосіб [1], являє собою циліндричну чарунку (ампулу) з робочою речовиною, по осі якої розташовано термометричний колодязь з платиновим термометром опору (ПТО) По периметру чарунки розташовано електричний нагрівач. Для відтворення реперної точки використовують температуру фазового переходу робочої речовини від твердого стану до рідкого або навпаки. Недоліком відомого способу є неврахування залежності температури фазового переходу неабсолютно чистої робочої речовини від співвідношення між рідкою і твердою фазами робочої речовини. Незнання цього співвідношення вносить похибку 0,5 + 5мК, що для еталона с відчутною величиною. В основу способу відтворення реперних точок міжнародної температурної шкали поставлено задачу підвищення точности визначення температури реперних точок міжнародної температурної шкали за рахунок зменшення похибки, пов'язаної з незнанням) зміною впродовж вимірювання температури співвідношення між рідкою і твердою фазами робочої речовини. Поставлена задача розв'язується тим, що, як реперну, використовують температуру гетерогенної фазової рівноваги з заданим співвідношенням між рідкою і твердою частинами (фазами), яке створюється шляхом введення у робочу речовину і підтримання сталою кількості теплової енергії, необхідної для розтоплення відповідної частини робочої речовини На фіг 1 подано еквівалентну теплову схему термостата з ампулою без робочої речовини. На фіг. 2 подано залежність потужності нагрівача і температури термостата, у який поміщено ампулу. На фіг. 3 подано ту ж саму еквівалентну схему, що і на фіг. 1, але з робочою речовиною, яка є частково розтоплена. На фіг. 4 подано ту ж саму схему, але з урахуванням, витікання теплової енергії через термометричний колодязь ампули. На фігурах зображено: 1 - нагрівач (електрична спіраль) термостата, зображений у вигляді еквівалентного джерела струму; 2 - тепловий опір між нагрівачем і металевим циліндром термостата; 3 чотириполюсник, який е еквівалентом стінки ампули з робочою речовиною; 4 - теплове навантаження підімкнене до виходу чотириполюсника 3; 5 - чотириполюсник, який є еквівалентом теплоізоляції термостата; 6 - теплове навантаження, підімкнене до виходу чотириполюсника 5 (тобто тепловий опір навколишнього середовища); 7 - робоча речовина, яка знаходиться у стані розтоплювання або кристалізації, зображена у вигляді еквівалентного джерела електрорушійної сили; 8 - чотириполюсник, який є еквівалентом теплової схеми термометричного колодязя разом з платиновим термометром опору, який у ньому знаходиться; 9 - теплове навантаження, підімкнене до виходу чотириполюсника 8 (тобто тепловий опір навколишнього середовища). Запропонований спосіб реалізується так. Робоча речовина знаходиться у спеціальній ампулі, по осі якої розташовано термометричний колодязь, у якому знаходиться платиновий термометр опору (ПТО). Ампула знаходиться в термостаті, який являє собою металевий циліндр, у стінках якого знаходиться електричний нагрівач. Від навколишнього середовища циліндр теплоізольовано. Термостат має електронну схему для підтримування заданої температури циліндра. Теплові провідності теплоізоляції (σ2), стінок ампули (σ1) і термометричного колодязя разом з термометром (σ3) у стаціонарному стані визначено заздалегідь. 1. Робоча речовина є нерозтоплена (знаходиться за кімнатної температури). 1.1. Встановлюють терморегулятор термостата на температуру Т 1 (дивіться формулу (39)), за якої, коли робоча речовина нагріється до температури топлення, теплова енергія у неї не поступатиме, і підмикають нагрівач 1 до джерела електроенергії. 1.2. Чекають, доки термостат (його металевий циліндр) нагріється до температури Т1, а робоча речовина - до температури топлення Wмет [тепер робоча речовина почне розтоплюватися, а середня J потужність, яка поступає у нагрівач, дорівнюватиме сер . , розрахованій за формулою (40)]. 1.3. Відмикають терморегулятор і в нагрівач 1 подають електричну потужність на певну величину (JZ) J більшу ніж сер . t J 1.4. Коли пройде час ( нгр ), визначений з формули (42), потужність нагрівача 1 зменшують до сер . і підтримують сталою, доки пройде перехідний процес (тобто, доки температура металевого циліндра знову стане рівна Т1). 1.5. Знову підмикають терморегулятор, встановлений на температуру Т1. 2. Робоча речовина знаходиться у рідкому стані і й температура є трохи вища за температуру кристалізації. 21 Встановлюють терморегулятор термостата на температуру Т 1 (дивіться формулу (39)), за якої, коли робоча речовина охолоне до температури топлення, теплова енергія у неї не поступатиме, і підмикають нагрівач 1 до джерела електроенергії. 22. Чекають, доки термостат (його металевий циліндр) охолоне до температури Т1, а робоча речовина до температури кристалізації Tмет . 2.3. Відмикають терморегулятор і в нагрівач 1 подають електричну потужність на певну величину (Jz J меншу ніж сер . J 2.4. Коли пройде час (t охл ). визначений з формули (46), потужність нагрівача 1 збільшують до сер . і підтримують сталою, доки пройде перехідний процес (тобто, доки температура металевого циліндра знову стане рівна Т1). 2.5. Роблять те ж саме, що і в пункті 1.5. Тепер реперна точка є готова до роботи з нею. Можна працювати впродовж тривалого часу (наприклад, впродовж 10 годин). При цьому точність відтворення реперної температури підвищиться у кілька десятків разів порівняно з відомими способами Теоретичне обґрунтування Ям відомо [2], якщо відтворювати реперну точку, використовуючи температуру кристалізації (топлення) робочої речовини, то температура кристалізації (топлення) залежатиме від співвідношення між рідкою і твердою фазами речовини. На практиці використовують не абсолютно чисті речовини, а речовини, які пройшли глибоке очищення, але містять певну кількість залишкових домішок. Якщо в експериментальних умовах забезпечено термодинамічну рівновагу твердої і рідкої фаз високочистої речовини то температура фазової рівноваги Т мінятиметься згідно з рівнянням: T = T0-N/(A f), (1) де: Τ0 - температура кристалізації абсолютно чистої робочої речовини; N - кількість домішок; А кріоскопічна стала; f = mрід/m - частка рідкої фази; mрід - маса рідкої (розтопленої) частини робочої речовини: m - маса всієї робочої речовини. Існують три методи реалізації реперних точок [2] і в кожному з них відтворюються температури, які відрізняються за термодинамічним змістом: приблизно Т0 - у потрійній точці, біля Tf- за кристалізації з внутрішнім ініціюванням і Τχ - за кристалізації з зовнішнім ініціюванням. При цьому найбільша неозначеність, пов'язана з Τχ, є обумовлена як можливими відхиленнями від термодинамічної рівноваги під час кристалізації, так і невизначеністю співвідношення твердої і рідкої фаз, за якого зроблено вимірювання Τχ. Отже, для забезпечення однозначної побудови і відтворення шкали необхідно конкретизувати температуру відтворення при реалізації реперної точки. Є можливі два варіанти: відтворення у всіх реперних точках Т0, аналогічно потрійній точці води, однак такий шлях практично важко реалізувати; відтворення Tf , що також практично важко реалізувати через труднощі внутрішнього ініціювання у речовин з великим переохолодженням. Тому оптимальним варіантом пропонується використання вимірювання температури гетерогенної фазової рівноваги з заданим співвідношенням між твердою і рідкою фазами, яке підтримується сталим впродовж всього періоду реєстрації температури. В цьому випадку е можливе перерахування на значення Tf і Т . 0 Коли ми нагріємо робочий метал до температури топлення, то ми введемо в нього певну кількість теплової енергії Потім метал почне розтоплюватись. Під час розтоплювання температура металу буде майже сталою. Для того, щоб розтопити m кг металу, ми повинні ввести в нього ще mq джоулів теплової енергії (тут q є питома теплота топлення металу). Якщо ми введемо в метал тільки частину необхідної енергії, то розтопиться тільки відповідна їй частина металу. Якщо метал е розтоплений (рідкий) і його температура не є вищою за температуру топлення робочого металу, то всьому знаходиться (крім теплової енергії, необхідно) для нагрівання металу до температури топлення) вся енергія, необхідна для того, щоб його повністю розтопити. Якщо ми випустимо якусь частину енергії, то відповідна їй частина металу стане і твердою. Q f =m q, (2) Q рід = m рід q. (3) Тут: Q f - теплова енергія, необхідна для того, щоб повністю розтопити робочий метал з масою m: q питома теплота топлення робочого металу; m рід - маса рідкої частини робочого металу; Q рід - частина енергії Q f , яка знаходиться у металі. З формул (3) і (2) знайдемо: m рід = Q рід /g; m = Q f /q. Тоді матимемо: s = m/m рід = Q f /Q рід (4) Тут s дорівнює 1/f у згаданій статті [2]. Отже, якщо задано величину з, то ми мусимо ввести в робочий метал або залишити у ньому (випустивши частину) (крім енергії, необхідної для нагрівання металу від кімнатної температури до його температури топлення) таку кількістьенергії: Q рід = Q f /s = m q/s. (5) Щоб це зробити, розгляньмо спочатку будову одного з можливих варіантів пристрою для відтворення реперної точки. Він являє собою металевий циліндр, у стінках якого знаходиться дріт з високим питомим опором для нагрівання циліндра електроенергією. Ця обмотка (назвімо її нагрівачем) е електричне ізольована від циліндра. Циліндр теплоізольовано від навколишнього середовища. В циліндр вставляють ампулу з робочим металом, по осі якої розташовано термометричний колодязь для платинового термометра опору. Температуру металевого циліндра міряють іншим термометром. Для спрощення розгляду теплових процесів у цьому пристрої розгляньмо його еквівалентну схему, подібну до електричних схем (див. фіг. 1). Тут тепловій потужності J відповідає електричним струм J е , тепловій енергії Q - електричний заряд Q е , температурі Т - електричний потенціал γ, температурному напорові w - електрична напруга υ, тепловому опорові R - електричний опір R е , тепловій провідності σ електрична провідність σ е , тепловій ємності С - електрична ємність C е , джерелу теплової енергії джерело електричного струму. Теплову ізоляцію між металевим циліндром і навколишнім повітрям розглядаймо як чотириполюсник 5 (див. фіг. 1) з апаратною функцією а2 (t). Її фур'є-образ є A 2(v). Стінку ампули з робочим металом також розглядаймо як чотириполюсник 3 з апаратною функцією a1(t) ft фур'е-образ е A1(v), де ν - частота , a t - час. Всередині цих чотириполюсників е тільки опори r1. r2 і ємності С1, С2. Джерело теплової енергії (нагрівач) зображено на цій схемі подібно до джерела струму 1, тепловий опір ізоляції між нагрівачем і циліндром зображено як опірник 2 (R). Вихід чотириполюсника 5 (еквівалентного теплоізоляції) навантажено опірником 6 (R2) еквівалентним тепловому опорові між поверхнею пристрою і навколишнім повітрям. Розгляньмо спочатку випадок, коли чотириполюсник 3 (еквівалентний стінці ампули) навантажено поки що тепловим опірником 4 (R1) (див. фіг. 1). Подаймо в нагрівач 1 від електромережі потужність J(t) впродовж певного часу t1, а потім вимкнімо її (див. фіг. 2). В точці D (металевий циліндр) температурний напір w(t) (різниця між температурою циліндра і кімнатною температурою ТК) спочатку зростатиме, а потім спаде до нуля (див. фіг. 2). В точці К (фіг. 1) температурний напір W К(t) дорівнюватиме математичній згортці температурного напору в точці D з апаратною функцією a1(t): Wk ( t ) = W ( t ) Ä a1( t ) , (6) Його фур'є-образ дорівнюватиме: Wk ( n ) = F( Wk ( t )) = W( n ) × A1( n ) , (7) тут літерою А позначено операцію фур’є-перетворення. Теплова потужність, яка проходитиме через опірник R1, дорівнюватиме: Ji(t) = Wk(t)/R1. (8) Щоб знайти теплову енергію, яка пройде через R1, проінтегруймо J1(t) по часу: ¥ ¥ Wk ( t ) 1 ¥ -J2 pn t Q1 = ò J1( t )dt = ò dt = dt ò Wk ( t ) × e -¥ -¥ R R1 - ¥ 1 n= 0 Звідси виходить, що 1 × F( Wk ( t ) R1 n =0 О1 = і, нарешті, підставивши (7) у попередню формулу, одержимо: 1 ( W (0 ) × A1(0 ) R1 О = . (9) 1 Але що являє собою W(0) ? Його можна записати так: ¥ W ( t ) × e-J 2pntdt -¥ W (0) = ò n =0 . (10) Тобто W(0) е фур'е-образ w(t) на нульовій частоті і він дорівнює: ¥ -¥ W ( 0) = ò W ( t ) dt . (11) А1(0) є фур'є-образ апаратної функції a1(t) за частоти рівної нулеві (тобто коли ємності С1 не беруть участи). З фіг.1 видно, що: R1 A1( 0 ) = R01 + R1 , (12) бо з формули (7) маємо: W (n ) A1( n ) = k W ( n) , (13) А це е коефіцієнт передач! чотириполюсника з апаратною функцією a1 (t) на частоті ν. А на нульовій частот! теплові ємності участи не беруть і, отже, матимемо формулу (12), де R01 є тепловий опір чотириполюсника 3 на нульовій частоті (тобто у стаціонарному режимі). Тоді A1(0)/R1, що входить до формули (9), дорівнюватиме: A1( 0 ) 1 = R1 R01 + R1 , (14) Тобто A1(0)/R1 є провідність правої галузки схеми (фіг.1) разом з R1 на нульовій частоті. Позначмо й через σ1. Тоді матимемо: Q1=W(0) σ1. (15) Подібно до цього, для лівої галузки схеми (Фіг. 1) матимемо: Q2 = W(0) σ2, (16) де σ2 = 1/(R02 + R2). За законом збереження енергії сумарна енергія обох галузок дорівнюватиме енергії, яку віддав у пристрій нагрівач: ¥ J( t ) dt . (17) Q n =Q1 + Q2 = ò-¥ Відношення енергій, які потрапили до правої і лівої галузок, дорівнюватиме: Q1 W( 0 ) × s1 s1 = = Q2 W (0 ) × s 2 s2 . (18) Звідси одержимо: s1 s 2 . (19) Підставивши формулу (19) у (17), одержимо: s s + s2 Qn = Q2 × 1 + Q2 = 1 × Q2 s2 s2 . (20) Q1 = Q2 × Остаточно матимемо: s2 Q2 = × Qn s1 + s2 . (21) Q1 = Qn - Q2 = s1 × Qn s1 + s2 . (22) Отже, енергія нагрівача 1 ділиться між двома галузками пропорційно їхнім провідностям на нульовій частоті. Якщо R1 або R2 дорівнюють нулеві, то σ1 = 1/R01, a σ2 = 1/R02Тепер розгляньмо схему реального пристрою, коли в ампулі є робочий метал, який почав розтоплюватися. Тоді температура металу дорівнюватиме його температурі топлення (яка приблизно буде сталою) і метал на схемі можна зобразити його еквівалентом 7, подібно до джерела електрорушійної сили, з тепловим напором Wмет (див. фіг. 3). Нехай в даний момент схема знаходиться в такому стаціонарному режимі, коли в метал теплова енергія не поступає. В цьому разі тепловий напір (W 0) у точці D (тобто, тепловий напір металевого циліндра) повинен дорівнювати тепловому напорові у точці К (тобто, тепловому напорові робочого металу 7): W = Wмет . (23) 0 Тоді потужність (J0), яку віддає нагрівач 1, повинна дорівнювати: J = σ Wмет . (24) 0 2 На ємностях (С1, С2) буде певна температура (стала в часі). Тепер, як і раніше, змінімо потужність нагрівача 1, повернувшись через деякий час до попереднього значення J0. Всі зміни енергій, потужностей і температур треба розглядати на тлі енергій, потужностей і температур цього стаціонарного режиму. Змінні величини позначаймо індексом z. Тоді змінна частина температурного напору у точці D дорівнюватиме W (t) = W(t) - Wмет . (25) Z а змінна частина потужності нагрівача 1: JZ(t) = J(t) – J0. (26) Тоді, подібно до попереднього, матимемо: ¥ 0 Qz1 = s1 × ò Wz ( t )dt . (27) ¥ 0 Qz 2 = s2 × ò Wz ( t )dt . (28) Але тепер σ1 = 1/R01 Додаткова (змінна) частина) енергії нагрівача 1 дорівнюватиме: ¥ 0 Q zn = Qz1 + Qz 2 = ò Jz ( t )dt . (29) Проробивши ті ж самі дії. що і у формулах (18)+(22), одержимо: s2 Qz 2 = × Qzn s1 + s 2 . (30) Qz1 = s1 × Qzn s1 + s 2 . (31) Тобто, в робочий метал потрапить частина додаткової (змінної) енергії нагрівача 1 пропорційна до теплової провідності (σ1) стінки ампули. Якщо потужність JZ(t) буде менша нуля (тобто в нагрівач подаватимемо впродовж певного часу потужність меншу ніж Jo), то енергія витече з металу 7 (QZ1 < 0), а в ліву галузку поступить енергії на QZ2 менше. Отже, якщо на тлі стаціонарних температур і потужностей ми зробимо зміни, повернувшись знову до попередніх значень, то додаткова енергія нагрівача 1 ділиться між галузками схеми так. ніби теплоємності у середовищі, через яке поширюється теплова енергія, є відсутні, а є тільки активні опори (r1 і r2, які легко піддаються визначенню). Але треба чекати, доки закінчаться перехідні процеси і схема повернеться знову до стаціонарного режиму. Тепер розгляньмо випадок, коли з ампули витікає теплова енергія. Те може відбуватися, наприклад, через термометричний колодязь. Середовище, через яке витікає енергія з ампули, зображено на Фіг.4 у вигляді чотириполюсника 8 з апаратною функцією aЗ(t), навантаженого на тепловий опір 9 (R3). Опір чотириполюсника 8 на нульовій частоті позначено, як R0З Коли режим буде стаціонарний, то через RЗ тектиме теплова потужність JЗ, рівна: J = Wмет σ , 32) З З Де σЗ = 1/(R03 + Rз). (33) Для вузла К матимемо: J1 + J мет = J 3. (34) Під час стаціонарного режиму J мет мусить дорівнювати нулеві. Тоді з формули (34) вийде: J1 + J 3 / (35) Тепер, під час стаціонарного режиму, температурний напір у вузлі D мусить дорівнювати: æ s ö J J J W = Wмет + 1 = Wмет + 3 = Wмет + Wмет 1 = ç 1+ 3 ÷ × Wмет s1 s1 s1 ç s1 ÷ ø è . (36) Потужність, яка витікає назовні через теплоізоляцію, дорівнюватиме: æ s ö J2 = W × s 2 = ç1 + 3 ÷ × s 2 × Wмет ç s1 ÷ ø è . (37) З попереднього виходить, що, під час стаціонарного режиму (а також під час робочого режиму), потужність нагрівача 1 (Jo) мусить дорівнювати: é æ s ö ù J0 = J1 + J2 = ês 3 + ç 1+ 3 ÷ s2 ú × Wмет ç s1 ÷ ú ê ø û è ë . (38) Щоб перейти до випадку, кол и можна знехтувати витіканням теплової енергії з ампули (наприклад, якщо тепловий опір термометра, який знаходиться у термометричному колодязі ампули, є дуже великий), достатньо σ3 прирівняти до нуля. Отже, ми повинні ввести у робочий метал, або залишити в ньому теплову енергію mq/s (крім енергії, необхідної для нагрівання робочого металу від кімнатної температури до його температури топлення)(див. формулу (6)). Автори пропонують зробити це так. Якщо робочий метал спочатку є твердий (нерозтоплений), то процедура буде така: 1). Встановлюють терморегулятор термостата на температуру: s J T1 = Tмет + 1 = Tмет + ( Tмет - Tk ) × 3 s1 s1 . (39) Чекають, доки термостат нагріється до задано температури Т1, (а робочий метал 7 нагріється до його температури топлення Т мет ). Тепер середня потужність нагрівача 1 дорівнюватиме: éæ s ö ù Jсер = ( Т1 - Т2 ) × s 2 + ( Тмет - Тk ) × êç 1+ 3 ÷ × s2 + s3 ú ÷ ç s1 ø êè ú . (40) ë û (в робочий метал енергія не входитиме, бо скільки теплової енергії входить у метал, стільки ж і витікає з нього). 2). Тепер вимикають терморегулятор і в нагрівач 1 подають потужність на певну величину (JZ) більшу J J =2 ), ніж сер . Чекають певний час ( E n×N потім перемикають потужність нагрівача 1 знову на сер . 3). Чекають, доки температура термостата (його металевого циліндра) знову стане рівна Т1. Потім знову вмикають терморегулятор, встановлений на температуру Т1. Після цих операцій у робочий метал увійде теплова енергія, рівна: s1 Q = Jz × tнгр × s1 + s 2 . (41) Взявши до уваги формулу (5), з формули (41) знайдемо енергію, яку треба подати у нагрівач 1. щоб забезпечити задане співвідношення а між рідкою і твердою частинами робочого металу: s + s 2 mq × Qz × t нгр = 1 s1 s . (42)' Якщо робочий метал спочатку розтоплено і нагріто до температури трохи вищої ніж температура топлення ( Tмет ). то процедура буде такою: 1). Встановлюють терморегулятор термостата на температуру: s T1 = Tмет + ( Т мет - Тk ) × 3 s1 . (43) Чекають, доки термостат охолоне до температури Т1, а робочий метал до Tмет . 2) Тепер вимикають терморегулятор і в нагрівач 1 подають потужність на певну величину (JZ) меншу ніж Jсер (t J . Чекають певний час охл ) , потім перемикають потужність нагрівача на сер 3). Чекають доки температура термостата (його металевого циліндра) знову стане рівна Т 1. Потім знову вмикають терморегулятор, встановлений на температуру Т1. Після цих операцій з робочого металу 7 витече енергія, рівна: s1 Q1 = J z × t охл × s1 + s 2 . (44) Тоді в металі 7 залишиться енергія (крім енергії, необхідної для нагрівання металу 7 до температури топлення): mq Q = m × q - Q1 = s . (45)' 3 (44); (45) одержимо: s + s2 æ 1 ö Jz × t охл = 1 × ç 1 - ÷ × mq s1 è sø . (46)' Тепер одержано числові величини, які покажуть доцільність і важливість застосування запропонованого способу. Для розрахунку візьмімо такі числові величини (близькі до реальності): Tмет = 419.5°С; Т = 20 °С; m = 2 кг; q = 118000 Дж/кг; s = 1,2; s1 = 1Вт/К; K s2 = 0,5 Вт/К; s3 = 0; t = 2 години - стала часу термостата; рід = Ю годин – можливий час роботи з реперною точкою; Е = 0,2 % - відносна похибка, з якою практично можна підтримувати потужність нагрівача 1; Е1 = 0,1; К - абсолютна похибка, з якою практично можна підтримувати температуру термостата (металевого циліндра); Візьмімо до уваги випадок, коли робочий метал спочатку був у твердому стані. Ставлять терморегулятор термостата на температуру Tмет і вмикають нагрівач. Термостат і робочий метал починають нагріватися Спочатку нагріється до Tмет термостат і далі його температура буде сталою. Поступово робочий метал в ампулі нагріється також до Tмет і почне розтоплюватися. Тепер середня потужність нагрівача дорівнюватиме: Jсер Tмет =( - ΤК) s2 В ампулу теплова енергія не тектиме. Тепер вимикають терморегулятор і збільшують потужність нагрівача 1 на певну величину ( Jz ), чекають t J певний час ( нгр ) і знову подають у нагрівач потужність сер , чекають, доки температура термостата знову стане рівна Tмет . У метал потрапить енергія, рівна: Qрід = Jz × t нгр × s1 s1 + s 2 . Q Енергія рід повинна дорівнювати mq/s. Отже матимемо: mq s1 + s2 × t нгр = s1 . sJz Тепер знову треба підімкнути терморегулятор, поставлений на Tмет . Реперна точка % готова. Тепер ми можемо міряти опір платинового термометра опору (ПТО) впродовж тривалого часу (наприклад, впродовж 10 год.). ( Jсер + Jz ) Коли подають у нагрівач потужність , то її можна підтримувати постійною з відносною похибкою Е = 0,2%. Абсолютна похибка дорівнюватиме: Jсер + Jz DPнгр = ×E 100 ( J + Jz ) нгр Тобто, впродовж часу t нгр У термостат потрапить енергії більше або менше, порівняно з сер t , на величину: Jсер + Jz DQнгр = D Pнгр × t нгр = × E × t нгр 100 А в робочий метал потрапить енергії більше або менше на: s1 DQ1 = DQнгр × s1 + s 2 . Підставивши у цю формулу одержані раніше вирази для Jсер + Jz mq DQ1( Jz ) = × E× 100 sJz DQ нгр і t нгр одержимо: J Впродовж перехідного процесу ( t ) потужність нагрівача 1 дорівнює сер і її підтримують також з відносною похибкою Е. Тоді впродовж часу τ у робочий метал потрапить або вийде з нього енергія, рівна: s1 Jсер DQ2 ( Jz ) = ×E×t s1 + s 2 . 100 Після того, як пройде час τ, ми вмикаємо терморегулятор, встановлений на температуру Т мет . Тепер температура термостата підтримується з абсолютною похибкою Е1 (наприклад, рівною 0,1 К). За робочий t час ( роб ) до металу додатково потрапить або вийде з нього енергія: DQ 3 = E1 × s1 × tроб Додавши всі три додаткові енергії D Q1, D Q2 і D Q3, ми одержимо абсолютну похибку введеної в метал Q теплової енергії рід : DQрід ( Jz ) = DQ1( Jz ) + D Q2 ( Jz ) + D Q3 Відносна похибка, з якою ми ввели енергію у робочий метал, дорівнюватиме: DQрід (Jz ) dQрід ( Jz ) = × 100 Qрід З такою ж відносною похибкою буде визначено і співвідношення s: ds(J z ) = dQрід ( Jz ) Абсолютна похибка, з якою буде визначено співвідношення а, дорівнюватиме: s × ds( Jz ) Ds( Jz ) = 100 Залежність температури топлення робочого металу від співвідношення з має такий вигляд (див. формулу (1)): N T = T0 - × s A Нас цікавитиме тільки змінний доданок у цій формулі Позначмо його літерою TS: N Ts = × s A Абсолютна похибка цього доданку дорівнюватиме: N DTs = × Ds A Відносна похибка, з якою можна визначити доданок Т S, дорівнюватиме: DT Ds dTs = s = = ds = dQрід Ts s Тобто точність (або відносна похибка), з якою ми можемо знати змінний доданок Т3, е така ж сама, з ямою ми мажемо ввести потрібну (для створення заданого співвідношення s) кількість теплової енергії Q рід . Величина (Ν/Α) становить приблизно (1 + 2)мК. Для обчислень візьмімо Ν/Α = 1,5. Тоді матимемо: DTs (J z ) = 1 .5 Ds( Jz ) . Якщо відтворювати реперну точку старим способом (тобто розтоплювати робочий метал з певною швидкістю, або охолоджувати розтоплений метал), то співвідношення s буде невідомим і може мінятися, наприклад, від 1 до 4. Тоді абсолютна похибка співвідношення з дорівнюватиме: D s=4–1=3 а абсолютна похибка змінного доданку Т З дорівнюватиме: D Ts=1.5 3=4.5 мК. Отже, виграш у абсолютній похибці відтворюваної температури дорівнюватиме: 4 .5 V( Jz ) = DTs (J z ) Проробімо розрахунки для різних значень Jz (наприклад, для 10,20,30,40,50 і 60 Вт). JZ dQрід (J z ) ds( Jz ) dTs ( Jz ) DTs ( Jz ) V( Jz ) 10 7.001 7.001 7.001 0.126 35.711 20 5.003 5.003 5.003 0.09 49.969 30 4.337 4.337 4.337 0.078 57.641 40 4.004 4.004 4.004 0.072 62.433 50 3.805 3.805 3.805 0.068 85.711 60 3.671 3.671 3.671 0.066 68.094 (Вт) (%) (%) (%) (мК) (рази) Якщо ми, наприклад, запізнимося з визначенням моменту, копи робочий метал нагрівся (або охолонув) Q до температури топлення (кристалізації) навіть на годину, то рід (а, отже, і s) зміниться всього на: E × s × 3600 dQрід.запізн. = 1 1 × 100 = 0. 183% Qрід Для випадку, коли робочий метал спочатку був у рідкому стані, похибка ( DT3 ) буде t ще менша, бо час t охл буде менший ніж нгр . Отже, запропонований спосіб дозволяє працювати з реперною точкою впродовж тривалого часу (порядку 10 годин) з заданим співвідношенням між рідкою і твердою фазами робочої речовини При цьому похибка відтворення температури, пов'язана з заданим співвідношення між рідкою і твердою фазами робочої речовини (як це відбувається у відомих способах), зменшується у кілька десятків разів. Крім того, виведення пристрою для відтворення реперної точки на робочий режим легко піддається автоматизації. ЛЯЕРАТУРА 1. Маркаріно П., Дематеїс Р. (Італія), "Реалізація МТШ-90 у діапазоні використання платинових термометрів опору зі стрижневим датчиком у інституті метрології "Дж.Колонетті” (ІMGC)". //Измерительная техника. 1993. №12. С. 68. 2. Александров Ю.І. та ін., "Температура реперної точки і й визначення”.// Измерительная техника. 1992. №5. С. 36.