Спосіб визначення параметрів нелінійної дисипативної коливальної системи
Формула / Реферат
Спосіб визначення параметрів нелінійної дисипативної коливальної системи, за яким формують чотири режими вимушених коливань, задають перше початкове ![]() і перше кінцеве
і перше кінцеве ![]() значення амплітуди вимушених коливань коливальної системи в першому і третьому режимах, в другому і четвертому режимах задають друге початкове
значення амплітуди вимушених коливань коливальної системи в першому і третьому режимах, в другому і четвертому режимах задають друге початкове ![]() і друге кінцеве
і друге кінцеве ![]() значення амплітуди вимушених коливань коливальної системи, перший і другий режими реалізують без зміни інерційності коливальної системи, третій і четвертий режими реалізують при зміні інерційності коливальної системи, при реалізації першого, другого, третього і четвертого режимів вимірюють і реєструють величини першого, другого, третього і четвертого часових інтервалів
значення амплітуди вимушених коливань коливальної системи, перший і другий режими реалізують без зміни інерційності коливальної системи, третій і четвертий режими реалізують при зміні інерційності коливальної системи, при реалізації першого, другого, третього і четвертого режимів вимірюють і реєструють величини першого, другого, третього і четвертого часових інтервалів ![]() ,
, ![]() ,
, ![]() ,
, ![]() і числа циклів
і числа циклів ![]() ,
, ![]() ,
, ![]() ,
, ![]() коливань у відповідних часових інтервалах, зміну частоти сигналу вимушеної дії при реалізації першого, другого, третього і четвертого режимів проводять із першою, другою, третьою і четвертою швидкостями
коливань у відповідних часових інтервалах, зміну частоти сигналу вимушеної дії при реалізації першого, другого, третього і четвертого режимів проводять із першою, другою, третьою і четвертою швидкостями ![]() ,
, ![]() ,
, ![]() ,
, ![]() зміни частоти відповідно, перший і третій, другий і четвертий часові інтервали реєструють при зміні амплітуди вимушених коливань від першого початкового до першого кінцевого значення, від другого початкового до другого кінцевого значення відповідно, фіксують і реєструють в кожному часовому інтервалі значення нижніх і верхніх частот, що відповідають зміні амплітудних значень вимушених коливань від відповідних початкових значень до відповідних кінцевих значень, який відрізняється тим, що додатково формують чотири групи режимів вимушених коливань по "
зміни частоти відповідно, перший і третій, другий і четвертий часові інтервали реєструють при зміні амплітуди вимушених коливань від першого початкового до першого кінцевого значення, від другого початкового до другого кінцевого значення відповідно, фіксують і реєструють в кожному часовому інтервалі значення нижніх і верхніх частот, що відповідають зміні амплітудних значень вимушених коливань від відповідних початкових значень до відповідних кінцевих значень, який відрізняється тим, що додатково формують чотири групи режимів вимушених коливань по "![]() " режиму вимушених коливань нелінійної дисипативної коливальної системи в кожній групі режимів, першу і другу групи режимів формують без зміни інерційності коливальної системи, третю і четверту групи режимів формують при зміні інерційності коливальної системи, в першій і третій групах режимів вимушених коливань задають перше початкове
" режиму вимушених коливань нелінійної дисипативної коливальної системи в кожній групі режимів, першу і другу групи режимів формують без зміни інерційності коливальної системи, третю і четверту групи режимів формують при зміні інерційності коливальної системи, в першій і третій групах режимів вимушених коливань задають перше початкове ![]() і перше кінцеве
і перше кінцеве ![]() значення відповідно амплітуди вимушених коливань коливальної системи, в другій і четвертій групах режимів вимушених коливань задають друге початкове
значення відповідно амплітуди вимушених коливань коливальної системи, в другій і четвертій групах режимів вимушених коливань задають друге початкове ![]() і друге кінцеве
і друге кінцеве ![]() значення відповідно амплітуді вимушених коливань, в першій, другій, третій і четвертій групах режимів частоту сигналу вимушеної дії змінюють із першою, другою, третьою і четвертою групами постійних в кожній групі але різних в різних групах швидкостей
значення відповідно амплітуді вимушених коливань, в першій, другій, третій і четвертій групах режимів частоту сигналу вимушеної дії змінюють із першою, другою, третьою і четвертою групами постійних в кожній групі але різних в різних групах швидкостей ![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() ) відповідно зміні частоти сигналу вимушеної дії, в першій, другій, третій і четвертій групах режимів вимушених коливань коливальної системи фіксують і реєструють інформаційні масиви (множину) часових інтервалів
) відповідно зміні частоти сигналу вимушеної дії, в першій, другій, третій і четвертій групах режимів вимушених коливань коливальної системи фіксують і реєструють інформаційні масиви (множину) часових інтервалів ![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() ) першої, другої, третьої і четвертої груп часових інтервалів відповідно і інформаційні масиви (множини) чисел
) першої, другої, третьої і четвертої груп часових інтервалів відповідно і інформаційні масиви (множини) чисел ![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() ) циклів коливань першої, другої, третьої і четвертої груп чисел циклів коливань відповідно, в першій, другій, третій і четвертій групах режимів вимушених коливань коливальної системи вимірюють і реєструють інформаційні масиви (множини) нижньої і верхньої частот
) циклів коливань першої, другої, третьої і четвертої груп чисел циклів коливань відповідно, в першій, другій, третій і четвертій групах режимів вимушених коливань коливальної системи вимірюють і реєструють інформаційні масиви (множини) нижньої і верхньої частот ![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() ),
),![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() ) відповідно до першої, другої, третьої і четвертої груп діапазонів частот відповідно, а визначення оцінки
) відповідно до першої, другої, третьої і четвертої груп діапазонів частот відповідно, а визначення оцінки ![]() резонансної частоти
резонансної частоти ![]() по
по ![]() -ій нормальній координаті проводять із співвідношення:
-ій нормальній координаті проводять із співвідношення:
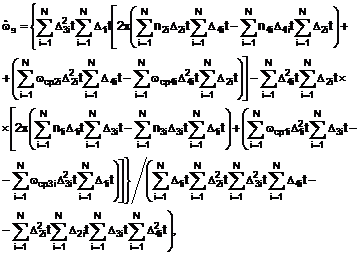
де ![]() ,
, ![]() ,
, ![]() ,
, ![]() - середні частоти першої, другої, третьої, четвертої груп відповідно діапазонів частот;
- середні частоти першої, другої, третьої, четвертої груп відповідно діапазонів частот;
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Текст
Спосіб визначення параметрів нелінійної дисипативної коливальної системи, за яким формують чотири режими вимушених коливань, задають перше початкове X a1 і перше кінцеве Xa2 значення амплітуди вимушених коливань коливальної системи в першому і третьому режимах, в другому і четвертому режимах задають друге початкове Xa3 і друге кінцеве Xa4 значення амплітуди вимушених коливань коливальної системи, перший і другий режими реалізують без зміни інерційності коливальної системи, третій і четвертий режими реалізують при зміні інерційності коливальної системи, при реалізації першого, другого, третього і четвертого режимів вимірюють і реєструють величини першого, другого, третього і четвертого часових інтервалів 1t , 2 t , 3 t , 4 t і числа циклів ної коливальної системи в кожній групі режимів, першу і другу групи режимів формують без зміни інерційності коливальної системи, третю і четверту групи режимів формують при зміні інерційності коливальної системи, в першій і третій групах режимів вимушених коливань задають перше початкове X a1 і перше кінцеве Xa2 значення відповідно амплітуди вимушених коливань коливальної системи, в другій і четвертій групах режимів вимушених коливань задають друге початкове Xa3 і друге n1 , n 2 , n 3 , n 4 коливань у відповідних часових інтервалах, зміну частоти сигналу вимушеної дії при реалізації першого, другого, третього і четвертого режимів проводять із першою, другою, третьою і четвертою швидкостями V1 , V2 , V3 , V4 зміни частоти відповідно, перший і третій, другий і четвертий часові інтервали реєструють при зміні амплітуди вимушених коливань від першого початкового до першого кінцевого значення, від другого початкового до другого кінцевого значення відповідно, фіксують і реєструють в кожному часовому інтервалі значення нижніх і верхніх частот, що відповідають зміні амплітудних значень вимушених коливань від відповідних початкових значень до відповідних кінцевих значень, який відрізняється тим, що додатково формують чотири групи режимів вимушених коливань по " N 1 " режиму вимушених коливань нелінійної дисипатив 4i t ( i 2, 3,...N ) першої, другої, третьої і четвертої груп часових інтервалів відповідно і інформаційні масиви (множини) чисел n1i , n 2i , n 3i , n 4i H3i , H4i ( i 2, 3,...N ), B1i , B2i , B3i , B 4i ( i 2, 3,...N ) відповідно до першої, другої, третьої і четвертої груп діапазонів частот відповідно, а виˆ значення оцінки S резонансної частоти S по S -ій нормальній координаті проводять із співвідношення: (13) 61967 (11) UA ( i 2, 3,...N ) циклів коливань першої, другої, третьої і четвертої груп чисел циклів коливань відповідно, в першій, другій, третій і четвертій групах режимів вимушених коливань коливальної системи вимірюють і реєструють інформаційні масиви (множини) нижньої і верхньої частот H1i , H2i , (19) ( i 2, 3,...N ) відповідно зміні частоти сигналу вимушеної дії, в першій, другій, третій і четвертій групах режимів вимушених коливань коливальної системи фіксують і реєструють інформаційні масиви (множину) часових інтервалів 1i t , 2i t , 3i t , U кінцеве Xa4 значення відповідно амплітуді вимушених коливань, в першій, другій, третій і четвертій групах режимів частоту сигналу вимушеної дії змінюють із першою, другою, третьою і четвертою групами постійних в кожній групі але різних в різних групах швидкостей V1i , V2i , V3i , V4i 3 61967 4 N N N N ˆ s 2 i t 1i t 2 n 2i 2i t 4i t 3 i 1 i 1 i 1 i 1 N N cp2i 2 i t 4i t 2 i 1 i 1 N N 2 n1i 1i t 3i t i 1 i 1 n N N N N N i 1 N N N i 1 2i t i 1 N i 1 2i t 2 i t 4 t 1i i 1 1i t 2 i t 2 i t 2 3 i 1 i 1 i 1 N N i 1 2i t i 1 N 3i 3i t i 1 N N n 4i 4i t N cp 4i 2 i t 4 i 1 cp3i 2 i t 1i t 3 i 1 i 1 N N N 2 cp1i 1i t 3i t i 1 N 4i t i 1 2 i t , 4 i 1 N 2 i t 2 i 1 2i t i 1 3i t i 1 де cp1i , cp2i , cp3i , cp4i - середні частоти першої, другої, третьої, четвертої груп відповідно діапазонів частот; Корисна модель належить до області машинобудівної, авіаційної і ракетно-космічної техніки, а саме, до способів визначення інерційножорсткісних параметрів нелінійних дисипативних коливальних систем із кінцевим числом ступенів вільності і може знайти застосування при проведенні вібраційних випробувань об'єктів на віброміцність, вібронадійність, вібростійкість і розробці нових технологій вібраційного типу. Відомий спосіб визначення параметрів нелінійної дисипативноїколивальної системи, за яким формують два режими вимушених коливань, в кожному режимі задають однакові початкові значення і однакові кінцеві значення амплітуд вимушених коливань коливальної системи, вимірюють величини першого і другого часових інтервалів 1t, 2t відповідно і числа циклів n1,n2 в часових інтервалах 1t, 2t відповідно при зміні амплітуди коливань в кожному часовому інтервалі від початкового до кінцевого значення, частоту сигналу збуджувальної дії в першому режимі змінюють із першою постійною швидкістю V1, в другому режимі - із другою постійною швидкістю V2, причому в першому і другому режимах фіксують значення середніх частот ср1, ср2 відповідно першого і другого діапазонів частот при зміні амплітуди вимушених коливань від постійного початкового значення Ха1 до постійного кінцевого значення Хa2, а визначення резонансної частоти s по s-ій нормальній координаті проводять із співвідношення: 2n1 n 2 cp11t cp2 2 t , s 1t 2 t cp1i 0,5H1i B1i , cp2i 0,5H2i B2i , cp3i 0,5H3i B3i , cp4i 0,5H4i B4i . де: cp1 1 H1 B1 , 2 1 H2 B2 , 2 H1, H2 - нижні частоти першого і другого діапазонів частот відповідно; В1, B2 - верхні частоти першого і другого діапазонів частот відповідно. (див. патент України на корисну модель №48344, М. кл. G01H11/00, 2010 рік) Недолік відомого способу визначення параметрів нелінійної дисипативної коливальної системи є недостатня точність визначення параметрів, що пояснюється неврахуванням похибок виміру, фіксації та запам'ятовування множини часових інтервалів та чисел циклів коливань при зміні амплітудних значень коливального процесу, а також недостатнім по множині інформаційним масивом часових інтервалів і чисел циклів коливань, що і приводить до наявності похибок вимірювання і реєстрації даних при формуванні алгоритму визначення параметрів. За прототип вибраний спосіб визначення параметрів нелінійної дисипативної коливальної системи, за яким формують два режими вимушених коливань, в кожному із режимів задають початкове і кінцеве значення амплітуд вимушених коливань нелінійної дисипативної коливальної системи, вимірюють величини першого і другого часових інтервалів 1t, 2t і числа циклів (періодів) n1,n2 коливань в цих часових інтервалах відповідно, змінюють частоту сигналу вимушеної дії при зміні амплітуди вимушених коливань в кожному часовому інтервалі від початкового до кінцевого значення в першому режимі із першою постійною швидкістю V1, а в другому режимі - із другою посcp2 5 тійною швидкістю V2, фіксують значення середніх частот ср1, ср2 в першому і другому режимах відповідно першого і другого діапазонів частот при зміні амплітуди вимушених коливань від початкового значення Ха1 до кінцевого значення Ха2, причому в першому і другому режимах вимушених коливань задають перше початкове і перше кінцеве Ха1, Ха2, друге початкове і друге кінцеве Ха3, Ха4 значення амплітуд вимушених коливань нелінійної дисипативної коливальної системи відповідно, змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по визначенню третього 3t і четвертого 4t часових інтервалів і чисел циклів n3,n4 коливань в цих часових інтервалах відповідно при зміні амплітуди вимушених коливань від її першого початкового значення Ха1 до першого кінцевого значення Ха2, від другого початкового значення Ха3 до другого кінцевого значення Ха4, фіксують в третьому і четвертому режимах значення середніх частот cp3, cр4 третього і четвертого діапазонів частот відповідно при зміні амплітуди вимушених коливань від першого початкового значення Ха1 до першого кінцевого значення Ха2 із третьою постійною швидкістю V3, від другого початкового значення Ха3 до другого кінцевого значення Ха4 із четвертою постійною швидкістю V4, а визначення резонансної частоти s по s-ій нормальній координаті проводять із співвідношення: s={3t[2(n2-n4)+cp22t-cp44t]-4t[2(n1n3)+cp11t-cp33t]}/{2t3t-1t4t); де B1 ; B2 ; cp1 H1 cp2 H2 2 2 H3 B3 ; H4 B4 . cp3 cp 4 2 2 H1, H2, H3, H4 - нижні частоти першого, другого, третього і четвертого діапазонів частот відповідно; B1, B2, B3, B4 - верхні частоти першого, другого, третього і четвертого діапазонів частот відповідно (див. рішення від 04.10.2010 року про видачу патенту на корисну модель за заявкою №u201006999). Недоліком відомого способу є те, що проводять однократне вимірювання і реєстрацію в кожному режимі кожного часового інтервалу, вимірювання і реєстрацію числа циклів коливань в цьому часовому інтервалі і однократне вимірювання нижніх і верхніх частот кожного діапазону частот при зміні частоти сигналу в кожному режимі із постійною швидкістю. При такому однократному вимірюванні випадкові похибки вимірювання і реєстрації приводять до зменшення точності визначення параметрів, а тому і області застосування способу. В основу корисної моделі поставлено задачу удосконалення способу шляхом підвищення точності визначення параметрів за рахунок формування розширених інформаційних масивів часових інтервалів, чисел циклів коливань при формуванні в кожному режимі інформаційного масиву постійної швидкості зміни частоти сигналу вимушеної дії при зміні амплітуди вимушених коливань в кожно 61967 6 му режимі від відповідного початкового значення до відповідного кінцевого значення при формуванні регресійних залежностей і застосуванні методу найменших квадратів. Поставлена задача вирішується тим, що у відомому способі, за яким формують чотири режими вимушених коливань, задають перше початкове Ха1 і перше кінцеве Ха2 значення амплітуди вимушених коливань коливальної системи в першому і третьому режимах, в другому і четвертому режимах задають друге початкове Ха3 і друге кінцеве Ха4 значення амплітуди вимушених коливань коливальної системи, перший і другий режими реалізують без зміни інерційності коливальної системи, третій і четвертий режими реалізують при зміні інерційності коливальної системи, при реалізації першого, другого, третього і четвертого режимів вимірюють і реєструють величини першого, другого, третього і четвертого часових інтервалів 1t, 2t, 3t, 4t і числа циклів n1,n2,n3,n4 коливань у відповідних часових інтервалах, зміну частоти сигналу вимушеної дії при реалізації першого, другого, третього і четвертого режимів проводять із першою, другою, третьою і четвертою швидкостями V1,V2,V3,V4 зміни частоти відповідно, перший і третій, другий і четвертий часові інтервали реєструють при зміні амплітуди вимушених коливань від першого початкового до першого кінцевого значення, від другого початкового до другого кінцевого значення відповідно, фіксують і реєструють в кожному часовому інтервалі значення нижніх і верхніх частот, що відповідають зміні амплітудних значень вимушених коливань від відповідних початкових значень до відповідних кінцевих значень, згідно з корисною моделлю, додатково формують чотири групи режимів вимушених коливань по "N1" режиму вимушених коливань нелінійної дисипативної коливальної системи в кожній групі режимів, першу і другу групи режимів формують без зміни інерційності коливальної системи, третю і четверту групи режимів формують при зміні інерційності коливальної системи, в першій і третій групах режимів вимушених коливань задають перше початкове Ха1 і перше кінцеве Ха2 значення відповідно амплітуді вимушених коливань коливальної системи, в другій і четвертій групах режимів вимушених коливань задають друге початкове Ха3 і друге кінцеве Ха4 значення відповідно амплітуді вимушених коливань, в першій, другій, третій і четвертій групах режимів частоту сигналу вимушеної дії змінюють із першою, другою, третьою і четвертою групами постійних в кожній групі але різних в різних групах швидкостей V1i,V2i,V3i,V4i (i=2,3, … N) відповідно зміни частоти сигналу вимушеної дії, в першій, другій, третій і четвертій групах режимів вимушених коливань коливальної системи фіксують і реєструють інформаційні масиви (множину) часових інтервалів 1it, 2it, 3it, 4it (i=2,3, … N) першої, другої, третьої і четвертої груп часових інтервалів відповідно і інформаційні масиви (множини) чисел n1i,n2і,n3і,n4i (і=2,3, … N) циклів коливань першої, другої, третьої і четвертої груп чисел циклів коливань відповідно, в першій, другій, третій і четвертій групах режимів вимушених коливань коливальної системи вимірюють і реєструють ін 7 61967 формаційні масиви (множини) нижньої і верхньої частот H1i, H2i, H3i, H4i (i=2,3, … N), B1i, B2i, B3i, B4i (i=2,3, … N) відповідно першої, другої, третьої і четвертої груп діапазонів частот відповід 8 ˆ но, а визначення оцінки s резонансної частоти s по s-ій нормальній координаті проводять із співвідношення: N N N N N N ˆ s 2 t 1it 2 n2i 2it 4it n4i 4it 2it 3i i 1 i 1 i 1 i 1 i 1 i 1 N N N N N N cp2i2 t 4it cp 4i2 t 2it 2 t 2it 2i 4i 4i i 1 i 1 i 1 i 1 i 1 i 1 N N N N N N 2 n1i1it 3it n3i3it 1it cp1i2 t 3it 1i i 1 i 1 i 1 i 1 i 1 i 1N N i 1 i 1 cp3i2 it 1it 3 N N N N t 2 t 2 t t 1i 2i 3i 4i i 1 i 1 i 1 i 1 N N N N i 1 i 1 i 1 i 1 2 it 2it 3it 2 it , 2 4 де cp1i, cp2i, cp3i, cp4i - середні частоти першої, другої, третьої, четвертої груп відповідно діапазонів частот; cp1i=0,5(H1i+B1i), cp2i=0,5(H2i+B2i), cp3i=0,5(H3i+B3i), cp4i=0,5(H4i+B4i). Застосування запропонованого способу разом з усіма суттєвими ознаками дозволяє вирішити поставлену технічну задачу. Пояснюється це розробленим новим алгоритмом визначення параметрів нелінійної дисипативної коливальної системи. Система базується на наступних аналітичних перетвореннях. При аналізі процесів у вібраційних машинах при умові взаємодії робочого органа (джерела механічної енергії) з коливальною системою проводиться рішення нелінійних диференціальних рівнянь (система приведена до нормальної форми) d2 Xk x 2 X k fk x, x, , , , , k 2 (1) dt k 1,n, d2 Xk x f x, x, , , , , dt 2 (2) де - малий позитивний параметр, що характеризує слабу нелінійність системи; Хk - координати; - координати обертального руху. Функції fk, f визначаються як періодичні з періодом 2 і такі, що диференціюються по аргументах (Пресняков В.К., Филер З.Е. Колебания механической системы, рассматриваемой совместно с двигателем. Динамика и прочность машин, Харьков, изд-во Харьковского университета, - 1971. c. 82. Кононенко В.О. Колебательные системы с ограниченным возбуждением, М.: "Наука", - 1964. c. 3035, 51-58. Кононенко В.О. Нелинейные колебания механических систем. Киев: "Наукова думка", 1980. c. 90-93, 95-100, 126-130, 201-210). Беручи до уваги умову, що внутрішні резонанси відсутні, проведемо аналіз системи в області близької до резонансної частоти по s-ій нормальp s q ), де p, q - взаємно прості ній координаті ( числа; - середня за період коливань швидкість (середня частота по діапазону частот). Рішення системи (1), (2) рівнянь має вигляд X s X a sin u1s X a , , , ..., X k u1k X a , , , ..., k s , p (3) , q d cp V1X a , , , ... dt Для функцій Ха, Θ, ср мають місце рівняння Xa A 1X a , , 2 A 2 ..., dt p d 2B ..., S B1X a , , 2 (4) dt q d 2 C ... C1X a , , 2 dt Приймаючи умову p=q=1 для першого наближення система рівнянь має вираз Xa d A 1 , S cp B1 , dt dt (5). dcp C1 . dt Проведемо нескладні перетворення системи (5). 1) Проведемо операцію ділення лівих і правих частин першого і другого рівняння системи (5) 9 61967 d S cp B dt 1. (6) dXa A 1 dt Після нескладних перетворень (6) отримаємо таке рівняння B d S dt cp dt 1 dXa , (7) A1 де dΘ=2dn, n - число циклів. Після інтегрування лівої і правої частини (7) отримаємо таке співвідношення X a2 B 2n S t cp t 1 dXa . (8) A1 X шеної дії (числа циклів n1,n3) і V2,V4 (числа циклів n2,n4) при зміні амплітуди вимушених коливань від першого початкового значення Ха1 до першого кінцевого значення Ха2 (числа циклів n1,n3, часові інтервали 1t, 3t), при зміні амплітуди вимушених коливань від другого початкового значення Ха3 до другого кінцевого значення Ха4 (числа циклів n2,n4, часові інтервали 2t, 4t); ср1, ср3 - середні частоти діапазонів частот, що відповідають часовим інтервалам 1t, 3t при зміні амплітуди вимушених коливань від першого початкового значення Ха1 до першого кінцевого значення Ха2 без зміни інерційності коливальної системи (середня частота ср1) і після зміни інерційності коливальної системи (середня частота ср3); ср2, ср4 - середні частоти діапазонів частот, що відповідають часовим інтервалам 2t, 4t без зміни інерційності коливальної системи (середня частота ср2) і після зміни інерційності коливальної системи (середня частота ср4) відповідно; s - резонансна частота системи по s-ій нормальній координаті без зміни інерційності; a1 При проведенні операцій по отриманню (8) не було застосовано третє рівняння системи (5). При застосуванні другого і третього рівнянь системи (5) отримаємо таке співвідношення B d S dt cp dt 1 dcp . (9) C1 Однак при застосуванні першого і третього рівнянь системи (5) отримаємо таке співвідношення C dcp 1 dXa . (10). A1 При застосуванні (9), (10) отримаємо співвідношення B C B d S dt cp dt 1 1 dXa 1 dXa ,(11) C1 A1 A1 тобто співвідношення (7) і (11) однакові. На підставі рівняння (8) отримаємо таку систему рівнянь: X a2 B 2n1 s 1t cp11t 1 dXa , (12) A X a1 1 2n 2 s 2 t cp2 2 t X a2 X a1 2n 3 s 3 t cp3 3 t X a2 X a1 2n 4 s 4 t cp4 4 t X a2 X a1 B1 dXa , A1 B1 dXa , A1 B1 dXa A1 10 s - резонансна частота системи по s-ій нормальній координаті після зміни інерційності. При проведенні вимірювань, фіксації, реєстрації інформаційних масивів груп часових інтервалів, чисел циклів коливань і груп нижніх і верхніх діапазонів частот, що відповідають зміні амплітуди вимушених коливань досліджуваної конструкції від відповідних початкових значень до відповідних кінцевих значень мають місце випадкові похибки. Тому на підставі системи рівнянь (12), (13), (14), (15) має місце наступна система рівнянь: X a2 B ˆ 2n1i s 1i t cp1i 1i t 1 dXa , (16) A X a1 1 ˆ 2n 2i s 2i t cp2i 2i t (13) X a4 X a3 ˆ 2n 3i s 3i t cp3i 3i t (14) X a2 X a1 ˆ 2n 4i s 4i t cp4i 4i t (15), X a3 B1 dXa , (18) A1 B1 dXa . (19). A1 На підставі рівнянь (16), (17), (18), (19) отримаємо наступні мінімізуючи функції: де n1,n2,n3,n4 - числа циклів (періодів) коливань в часових інтервалах 1t, 2t, 3t, 4t відповідно при реалізації режимів вимушених коливань із швидкостями: V1,V3 зміни частоти сигналу виму2 X a2 N B1 ˆ S1 2n1i s 1i t cp1i 1i t dXa , A1 i 1 X a1 X a4 N B ˆ S 2 2n 2i s 2i t cp2i 2i t 1 dXa A i 1 X a3 1 X a4 B1 dXa , (17) A1 (20) 2 , (21) 11 61967 2 X a2 N B1 2n t , ˆ S3 dXa 3i s 3i cp3i 3i t A1 i 1 X a1 2 X a4 N B1 2n t , ˆ S4 dXa 4i s 4i cp4i 4i t A i 1 X a3 1 ˆ ˆ де N - число експериментів; s , s - оцінки частот s, s відповідно. Після формування частинних похідних 12 (22) (23) ˆ ˆ них рівнянь відносно оцінок s , s частот s, s : S1 , ˆ s S 2 S 4 S 3 , , отримаємо систему нормальˆ s s s Xa 2 N S1 B ˆ 0 2n1i s1it cp1i1it 1 dXa 1it 0 , ˆ s A i 1 X a1 1 (24) Xa 4 N S2 B ˆ 0 2n2i s 2it cp2i 2it 1 dXa 2it 0 , ˆ s A i1 Xa 3 1 (25) Xa 2 N S3 B ˆ 0 2n3i s3it cp3i3it 1 dXa 3it 0 , s A i1 X a1 1 (26) Xa 4 N S 4 B ˆ 0 2n4i s 4it cp 4i 4it 1 dXa 4it 0 , s A i1 Xa 3 1 (27) Xa 2 N N N N B ˆ 2 n1i1it s 2 t cp1i2 t 1it 1 dXa 0 , 1i 1i A i 1 i 1 i 1 i 1 Xa1 1 (28) Xa 4 N N N N B ˆ 2 n2i2it s 2 t cp2i2 t 2it 1 dXa 0 , 2i 2i A i1 i1 i1 i1 Xa 3 1 (29) Xa 2 N N N N B ˆ 2 n3i3it s 2 t cp3i2 t 3it 1 dXa 0 , 3i 3i A i1 i1 i1 i1 X a1 1 (30) Xa 4 N N N N B ˆ 2 n4i 4it s 2 t cp4i2 t 4it 1 dXa 0 . 4i 4i A i1 i1 i1 i1 Xa 3 1 (31) Для виключення інтегральних складових в системі (28)-(31) рівнянь проведемо нескладні перетворення: N N N N ˆ 2 n1i 1i t s 2 t cp1i 2 t 1i t 1i 1i i 1 i 1 i 1 i 1 ; N N N N ˆ 2 n 3i 3i t s 2 t cp3i 2 t 3i t 3i 3i i 1 i 1 i 1 i 1 (32) 13 61967 N N N N ˆ 2 n 2i 2i t s 2 t cp2i 2 t 2i t 2i 2i i 1 i 1 i 1 i 1 . N N N N 2 t ˆ 2 t 2 n 4i 4i t s 4i t cp 4i 4i 4i i 1 i 1 i 1 i 1 14 (33) Із системи (32), (33) отримаємо таку систему ˆ двох рівнянь відносно s , s : N N N N N N ˆ 2 n1i1it 3it s 2 t 3it cp1i2 t 3it 1i 1i i 1 i 1 i 1 i 1 i 1 i 1 N N N N N N 2 t t 2 t t; ˆ 2 n3i3it 1it s 1i cp3i 1i 3i 3i i 1 i 1 i 1 i 1 i 1 i 1 N N N N N N 2 t t 2 t t ˆ 2 n2i 2it 4it s 4i cp2i 4i 2i 2i i 1 i 1 i 1 i 1 i 1 i 1 N N N N N N ˆ n4i 4it 2it s 2 t 2it cp4i2 t 2it, 4i 4i i 1 i 1 i 1 i 1 i 1 i 1 N N N N N N ˆ ˆ s 2 t 3it s 2 t 1it 2 n1i1it 3it 1i 3i i1 i1 i1 i1 i1 i1 N N N N N N n3i3it 1it cp1i2 t 3it cp3i2 t 1it ; 1i 3i i1 i1 i1 i1 i1 i1 N N N N N N 2 t t ˆ 2 t t 2 n t t ˆ s 4i s 2i 2i 2i 4i 2i 4i i1 i1 i1 i1 i1 i1 N N N N N N 2 t t 2 t t , n4i 4it 2it cp2i 4i cp4i 2i 2i 4i i1 i1 i1 i1 i1 i1 (34) (35) Із системи (35) рівнянь отримаємо аналітичні ˆ ˆ співвідношення визначення N оцінок s , s : N N N N N N ˆ s 2 t 1it 2 n2i 2it 4it n4i 4it 2it 3i i1 i1 i1 i1 i1 i1 N N N N N N cp2i2 t 4it cp 4i2 t 2it 2 t 2it 2i 4i 4i i1 i1 i1 i1 i1 i1 N N N N N N 2 n1i1it 3it n3i3it 1it cp1i2 t 3it 1i i1 i1 i1 i1 i1 i1 N N cp3i2 t 1it 3i i1 i1 N N N N t 2 t 2 t t 1i 2i 3i 4i i1 i1 i1 i1 N N N N 2 t 2it 3it 2 t ; 2i 4i i1 i1 i1 i1 (36) 15 61967 N N N N N N ˆ s 2 t 3it 2 n2i 2it 4it n4i 4it 2it 1i i1 i1 i1 i1 i1 i1 N N N N N N cp2i2 t 4it cp 4i2 t 2it 2 t 4it 2i 4i 2i i1 i1 i1 i1 i1 i1 N N N N N N 2 n1i1it 3it n3i3it 1it cp1i2 t 3it 1i i1 i1 i1 i1 i1 i1 N N cp3i2 t 1it 3i i1 i1 16 (37) N N N N t 2 t 2 t t 1i 2i 3i 4i i1 i1 i1 i1 N N N N 2 t 2it 3it 2 t . 2i 4i i1 i1 i1 i1 Спосіб визначення параметрів нелінійної дисипативної коливальної системи реалізують на підставі наступного алгоритму. Інформують чотири групи режимів вимушених коливань нелінійної коливальної системи: а) в першій групі "N" режимів частоту сигналу вимушеної дії змінюють із першою групою постійних швидкостей V1i (i=1, … N), задають перше початкове і перше кінцеве значення Xa1,Xa2 відповідно амплітуді вимушених коливань коливальної системи; б) вимірюють і реєструють часові інтервали 1it (i=1, … N) першої групи часових інтервалів і числа n1i (i=1, … N) циклів коливань першої групи чисел циклів коливань в часових інтервалах 1it при зміні амплітуди вимушених коливань від першого початкового значення Ха1 до першого кінцевого значення Ха2 при зміні частоти сигналу вимушеної дії із першою групою постійних швидкостей V1i (і=1, … N); в) вимірюють і реєструють нижню і верхню частоти H1i, B1i (i=1, … N) відповідно першої групи діапазонів частот, що відповідає інтервалу зміни амплітуди вимушених коливань від першого початкового значення Ха1 до першого кінцевого значення Ха2 при зміні частоти сигналу вимушеної дії із першою групою постійних швидкостей V1i (і=1, … N). 2). Формують другу групу "N" режимів вимушених коливань: а) в другій групі режимів частоту сигналу вимушеної дії змінюють із другою групою постійних швидкостей V2i (і=1, … N), задають друге початкове і друге кінцеве значення Ха3, Ха4 відповідно амплітуди вимушених коливань коливальної системи; б) вимірюють і реєструють часові інтервали Δ2it (i=1, … N) другої групи часових інтервалів і числа n2i (i=1, … N) циклів коливань другої групи чисел циклів коливань в часових інтервалах 2it при зміні амплітуди вимушених коливань від другого початкового значення Ха3 до другого кінцевого значення Ха4 при зміні частоти сигналу вимушеної дії із другою групою постійних швидкостей V2i (і=1, … N); в) вимірюють і реєструють нижню і верхню частоти H2i, B2i (i=1, … N) відповідно другої групи діапазонів частот, що відповідає інтервалу зміни амплітуди вимушених коливань від другого початкового значення Ха3 до другого кінцевого значення Ха4 при зміні частоти сигналу вимушеної дії із другою групою постійних швидкостей V2i (і=1, … N). 3). Змінюють інерційність нелінійної дисипативної коливальної системи. Формують третю групу "N" режимів вимушених коливань: а) в третій групі режимів частоту сигналу вимушеної дії змінюють із третьою групою постійних швидкостей V3i (і=1, … N), задають перше початкове і перше кінцеве значення Ха1, Ха2 відповідно амплітуді вимушених коливань коливальної системи із зміненою інерційністю; б) вимірюють і реєструють часові інтервали 3it (i=1, … N) третьої групи часових інтервалів і числа n3i (i=1, … N) циклів коливань третьої групи чисел циклів коливань в часових інтервалах 3it при зміні амплітуди вимушених коливань від першого початкового значення Ха1 до першого кінцевого значення Ха2 при зміні частоти сигналу вимушеної дії із третьою групою постійних швидкостей V3i (і=1, … N); в) після зміни інерційності нелінійної коливальної системи, вимірюють і реєструють нижню і верхню частоти H3i, B3i (i=1, … N) відповідно третьої групи діапазонів частот, що відповідає інтервалу зміни амплітуди вимушених коливань від першого початкового значення Ха1 до першого кінцевого значення Ха2 при зміні частоти сигналу вимушеної дії із третьою групою постійних швидкостей V3i (і=1, … N). 4). Формують четверту групу "N" режимів вимушених коливань: а) в четвертій групі режимів частоту сигналу вимушеної дії змінюють із четвертою групою постійних швидкостей V4i (і=1,2, … N), задають друге початкове і друге кінцеве значення Ха3, Ха4 відповідно амплітуді вимушених коливань коливальної системи із зміненою інерційністю; б) вимірюють і реєструють часові інтервали 4it (і=1,2, … N) четвертої групи часових інтервалів і числа n4i (i=1, … N) циклів коливань четвертої групи чисел циклів коливань в часових інтервалах 4it при зміні амплітуди вимушених коливань від другого початкового значення Ха3 до другого кін 17 61967 цевого значення Ха4 при зміні частоти сигналу вимушеної дії із четвертою групою постійних швидкостей V4i (і=1,2, … N); в) після зміни інерційності нелінійної коливальної системи, вимірюють і реєструють нижню і верхню частоти H4i, B4i (i=1, … N) відповідно до четвертої групи діапазонів частот, що відповідає інтервалу зміни амплітуди вимушених коливань від другого початкового значення Ха3 до другого кінцевого значення Ха4 при зміні частоти сигналу вимушеної дії із четвертою групою постійних швидкостей V4i (і=1,2, … N). Спосіб визначення параметрів нелінійної коливальної системи реалізують наступним чином. 1). Установлюють досліджуваний об'єкт (конструкцію) на рухому платформу вібростенда електродинамічного типу. 2). Послідовно реалізують першу, другу, третю та четверту групи режимів вимушених коливань конструкції, а в кожній групі режимів формують "N" повторень процесу, причому в першій і третій групах режимів із "N" повторень кожний фіксують і реєструють постійне перше початкове значення амплітуди Ха1 сигналу вимушених коливань конструкції і постійне перше кінцеве значення амплітуди Ха2 сигналу вимушених коливань конструкції, в другій і четвертій групах режимів із "N" повторень кожний фіксують і реєструють постійне друге початкове значення амплітуди Ха3 вимушених коливань конструкції і постійне друге кінцеве значення амплітуди Ха4 сигналу вимушених коливань конструкції. 3). Першу і другу групи режимів вимушених коливань досліджуваної конструкції реалізують без зміни інерційності рухомої частини конструкції, другу і четверту групи режимів вимушених коливань реалізують після зміни інерційності рухомої частини конструкції. 4). В першій групі режимів вимушених коливань із "N" повторень частоту сигналу вимушеної дії змінюють із першою групою постійних швидкостей V1i (і=1, … N), в другій групі режимів iз "N" повторень частоту сигналу вимушеної дії змінюють із другою групою постійних швидкостей V2i (і=1, … N), в третій групі режимів iз 3 "N" повторень частоту сигналу вимушеної дії змінюють із третьою групою постійних швидкостей V3i (і=1, … N), в четвертій групі режимів із "N" повторень частоту сигналу вимушеної дії змінюють із четвертою групою постійних швидкостей V4i (і=1, … N). 5) В першій і третій групах режимів вимушених коливань iз "N" повторень кожний вимірюють, фіксують і реєструють першу і третю групи 1it, 3it (1,2, … N) часових інтервалів відповідно із "N" інтервалів кожна група і відповідні першу і третю групи чисел n1i, n3i (1,2, …. N) циклів коливань відповідно із "N" циклів кожна група при зміні частоти Комп’ютерна верстка М. Ломалова 18 сигналу вимушеної дії із першою і третьою групами постійних швидкостей V1i, V3i (1,2, … N) зміни частоти відповідно при зміні амплітуди сигналу вимушених коливань від першого постійного початкового значення Ха1 до першого постійного кінцевого значення Ха2. 6). В другій і четвертій групах режимів вимушених коливань із "N" повторень кожний вимірюють, фіксують і реєструють другу і четверту групи 2it, 4it (1,2, … N) часових інтервалів із "N" інтервалів кожна група і відповідні другу і четверту групи чисел n2i, n4i (1,2, … N) циклів коливань із "N" циклів кожна група при зміні частоти сигналу вимушеної дії із другою і четвертою групами постійних швидкостей V2i, V4i (1,2, … N) зміни частоти відповідно при зміні амплітуди сигналу вимушених коливань від другого постійного початкового значення Ха3 до другого постійного кінцевого значення Ха4. 7). В першій, другій, третій і четвертій групах режимів вимушених коливань досліджуваної конструкції вимірюють, фіксують і реєструють інформаційні масиви груп нижніх і верхніх частот діапазонів частот відповідно групам режимів, причому в першій групі режимів реєструють першу групу нижніх частот H1i (i=1, … N) і першу групу верхніх частот B1i (i=1, … N), в другій групі режимів реєструють другу групу нижніх частот H2i (i=1, … N) і другу групу верхніх частот B2i (i=1, … N), в третій групі режимів реєструють третю групу нижніх частот H3i (i=1, … N) і третю групу верхніх частот B3i (i=1, … N), в четвертій групі режимів реєструють четверту групу нижніх частот H4i (i=1, … N) і четверту групу верхніх частот B4i (i=1, … N). 8). За допомогою вимірювальнообчислювального комплексу (комп'ютерної системи) проводять обробку інформаційного масиву зареєстрованих сигналів Δ1it, Δ2it, Δ3it, Δ4it, n1i, n2і, n3i, n4і; H1i, H2i, H3i, H4i; B1i, B2i, B3i, B4i (i=1,…, N). На підставі отриманого нового аналітичного співвідношення визначають оцінки значення параметрів досліджуваного об'єкта (конструкції) при урахуванні випадкових похибок вимірювання і реєстрації і при умові застосування джерел енергії обмеженої потужності, а саме, значення оцінки резонансної частоти 1s по s-ій нормальній координаті досліджуваної конструкції при урахуванні умови застосування джерела енергії обмеженої потужності. Таким чином, використання заявлюваного способу дає можливість отримувати достатню точність при оцінці інерційно-жорсткісних параметрів нелінійних коливальних систем із кінцевим числом степенів вільності. Підписне Тираж 23 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determination of parameters of non-linear dissipative oscillatory system
Автори англійськоюPuz'ko Ihor Danylovych
Назва патенту російськоюСпособ определения параметров нелинейной диссипативной колебательной системы
Автори російськоюПузько Игорь Данилович
МПК / Мітки
МПК: G01H 11/00
Мітки: коливальної, параметрів, дисипативної, нелінійної, системі, спосіб, визначення
Код посилання
<a href="https://ua.patents.su/9-61967-sposib-viznachennya-parametriv-nelinijjno-disipativno-kolivalno-sistemi.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення параметрів нелінійної дисипативної коливальної системи</a>
Попередній патент: Пристрій для наповнення клапанних мішків сипучим матеріалом
Наступний патент: Пристрій для запобігання буксуванню коліс локомотива
Випадковий патент: Спосіб одержання вологостійкого виробу на основі гіпсу (варіанти), спосіб уведення силоксану при одержанні вологостійкого виробу на основі гіпсу та плита на основі гіпсу













