Спосіб формування аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої арифметики

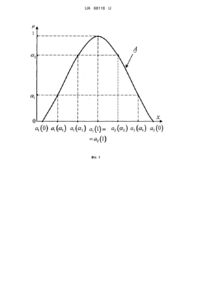
Реферат: Спосіб формування аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої арифметики, згідно з яким, забезпечують попередню перевірку властивостей нормальності та опуклості первинних нечітких множин. UA 68118 U (54) СПОСІБ ФОРМУВАННЯ АНАЛІТИЧНИХ МОДЕЛЕЙ РЕЗУЛЬТУЮЧИХ НЕЧІТКИХ МНОЖИН ПРИ РЕАЛІЗАЦІЇ ОПЕРАЦІЙ НЕЧІТКОЇ АРИФМЕТИКИ UA 68118 U UA 68118 U 5 10 15 20 25 Корисна модель належить до обчислювальної техніки, а саме до моделювання керованих процесів і об'єктів, що функціонують в умовах невизначеності, й може бути використана для групової обробки нечіткої інформації, зокрема, для синтезу моделей, що забезпечують автоматичне визначення ступеня приналежності відповідних параметрів або показників до результуючих нечітких множин, сформованих для здійснення операцій нечіткої арифметики. Відомо про способи формування аналітичних моделей керованих об'єктів і процесів, що забезпечують уточнення і корекцію моделей в процесі функціонування об'єктів керування. Прикладом таких способів є спосіб формування нелінійного об'єкта визначеної поведінки [патент України № 71232, G06П 7/30, Бюл. № 11, 2004], що передбачає оцінку поведінки спектрзображення, яке досліджується за коливальністю, дисперсністю руху елементів, інваріантністю за напрямком зміни аргументу, інформаційною відстанню при дослідженні частотних спектрів, селективною ентропією, складністю опису з організацією робастного пошуку коефіцієнтів полінома та встановленням відповідності за узагальненим критерієм, який передбачає часткову відповідність опису об'єкта за поведінкою в часі та частотою діянь, характером кривизни досліджуваної залежності, та у разі невдалого висновку передає дію на реконструкцію полінома у вигляді адитивних сумішей елементів вищих порядків та функціональних залежностей відмінної форми та гладкості. Такий спосіб не забезпечує можливість формування аналітичних моделей для обробки нечіткої інформації, що суттєво обмежує область його практичного застосування. Відомо також про способи формування аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої арифметики, які в більшості випадків забезпечують формування тільки інверсних (горизонтальних) результуючих моделей при виконанні операцій нечіткої арифметики, зокрема, додавання, віднімання, множення або ділення. Для практичного ж використання в системах автоматичного керування в умовах невизначеності та в інтелектуальних системах обробки нечіткої інформації необхідним є формування прямих (вертикальних) результуючих нечітких множин, що забезпечують пряме визначення ступеня істинності C z    A  B z  входження відповідного параметра чи показника х до результуючої ~ ~ ~ ~ ~ нечіткої множини C  AB , що формується при здійсненні відповідної арифметичної операції ~  над первинними нечіткими множинами. 30 35 Найбільш близьким до запропонованого є спосіб формування аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої арифметики [Kaufmann A., Gupta, M. Introduction to Fuzzy Arithmetic: Theory and Applications. Van Nostrand Reinhold Company, New York 1985, стор. 25-27], що прийнятий як прототип. Згідно з цим способом формування аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої арифметики послідовно вибирають форму функцій належності та параметри первинних нечітких множин A , B , над якими планують здійснення однієї з операцій нечіткої арифметики   ,,*, / , 40 45 50 55 ~ ~ зокрема, додавання, віднімання, множення або ділення, формують прямі (вертикальні) аналітичні моделі первинних нечітких множин, на основі яких формують інверсні (горизонтальні) аналітичні моделі первинних нечітких множин з використанням узагальнених горизонтальних -перерізів, вибирають необхідну операцію нечіткої арифметики для первинних нечітких множин, формують аналітичну інверсну модель функції належності результуючої нечіткої множини на основі інверсних моделей первинних нечітких множин, використовуючи при цьому механізм реалізації відповідної операції нечіткої арифметики на основі застосування перерізів, а в подальшому формують пряму аналітичну модель функції належності результуючої нечіткої множини у вигляді точної аналітичної або апроксимованої математичної залежності. Такий спосіб при використанні відмінних від трикутних форм функцій належності первинних нечітких множин не забезпечує попередньої перевірки властивостей нормальності та опуклості первинних нечітких множин, а також не забезпечує перевірки адекватності синтезованих моделей шляхом проведення тестових випробувань з подальшою корекцією синтезованих моделей, що в багатьох випадках знижує необхідний рівень точності обчислювальних процесів і обмежує використання синтезованих моделей для обробки нечіткої інформації в реальному часі. Відсутність перевірки функцій належності первинних нечітких множин на нормальність та опуклість може призвести до неможливості або до суттєвого ускладнення задач формування аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої арифметики. В основу корисної моделі поставлено задачу удосконалення способу формування аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої 1 UA 68118 U 5 10 15 20 25 30 арифметики шляхом забезпечення попередньої перевірки властивостей нормальності та опуклості первинних нечітких множин, покрокової перевірки адекватності синтезованих моделей на основі їх тестування та циклічної корекції синтезованих моделей до виконання умови забезпечення необхідного порогу точності, що відіграє роль критерію адекватності моделей. Поставлена задача вирішується тим, що при реалізації способу формування аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої арифметики, згідно з яким послідовно вибирають форму функцій належності та параметри первинних нечітких множин, над якими планують здійснення однієї з операцій нечіткої арифметики, зокрема, додавання, віднімання, множення або ділення, формують прямі (вертикальні) аналітичні моделі первинних нечітких множин, на основі яких формують інверсні (горизонтальні) аналітичні моделі первинних нечітких множин з використанням узагальнених горизонтальних -перерізів, вибирають необхідну операцію нечіткої арифметики для первинних нечітких множин, формують аналітичну інверсну модель функції належності результуючої нечіткої множини на основі інверсних моделей первинних нечітких множин, використовуючи при цьому механізм реалізації відповідної операції нечіткої арифметики на основі застосування -перерізів, а в подальшому формують пряму аналітичну модель функції належності результуючої нечіткої множини у вигляді точної аналітичної або апроксимованої математичної залежності, згідно до пропозиції попередньо перевіряють забезпечення властивостей нормальності та опуклості первинних нечітких множин, здійснюють ряд тестових випробувань для перевірки адекватності синтезованих моделей, для чого задають ряд тестових значень -рівнів в межах інтервалу від нуля до одиниці, для яких за інверсною моделлю функції належності результуючої нечіткої множини визначають у вигляді закритих інтервалів діапазони існування носіїв нечітких підмножин зі ступенем істинності, що є не меншим від вибраного на відповідному кроці тестування -рівня, для сформованих граничних значень кожного з закритих інтервалів відповідних носіїв нечітких підмножин визначають два значення ступенів істинності відповідно до лівої і правої гілок функції належності при використанні синтезованої прямої аналітичної моделі результуючої нечіткої множини, задають допустимі порогові значення похибок, а в подальшому контролюють величини розугоджень між отриманими значеннями ступенів істинності для границь закритих інтервалів та початковими тестовими значеннями відповідних -рівнів, у випадку перевищення контрольованими похибками попередньо заданих порогових значень здійснюють корекцію синтезованої прямої аналітичної моделі функції належності результуючої нечіткої множини і повторюють процедуру її тестових випробувань, які завершують при умові, що всі похибки знаходяться в межах допустимих порогових значень. На фіг. 1 представлена функція належності  A x  первинної нечіткої множини A з ~ ~ 35 ілюстрацією 4-х -перерізів,   0, 1, 2,1 та відповідних діапазонів існування носія х у вигляді a1, a2  для нечітких підмножин sup pA  z, z  a11, a2 1, sup pA0  z, z  a10, a2 0 , sup pA1  z, z  a11, a2 1, при цьому а1(1)=а2(1); на фіг. закритих інтервалів 1 A  0, A 1 , A  2 , A  1 , зокрема, sup pA 2  z, z  a12 , a2 2  , 2 наведені інверсна C та ~ апроксимована пряма C * моделі результуючої нечіткої множини C  A*B , які ілюструють ~ ~ 40 45 ~ ~ розугодження між прямою та інверсною моделями, зокрема для лівої гілки функції належності L  f1 a, b, c1 j    j,  j  0,515 та для правої гілки функції належності   R  f2 a, b, c 2  j1   j1,  j1  0,455 . Запропонований спосіб формування аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої арифметики здійснюється наступним чином. Для здійснення однієї з операцій нечіткої арифметики (додавання, віднімання, множення або ділення) над первинними нечіткими множинами A , B перш за все формують самі первинні ~ ~ нечіткі множини, для чого вибирають форму (трикутна, трапеційна, гаусівська, дзвоноподібна тощо) та параметри a, b функцій належності первинних нечітких множин A , B , де A,B  R , a ~ ~ ~ ~ вектор параметрів функції належності первинної нечіткої множини A ; b - вектор параметрів ~ 50 функції належності первинної нечіткої множини B . Нечітку множину ~ A ~ представляють + сукупністю пар чисел  x,  A x  , де х - значення нечіткого параметра xR , який належить    ~  2 UA 68118 U множині дійсних додатних чисел R ;  A x  - відповідне значення функції належності для + ~ параметра х,  A x   0,1 . Нечітку множину B представляють сукупністю відповідних пар чисел ~ ~  y,  y  , де у - значення нечіткого параметра yR+, який належить множині дійсних додатних   B ~   + чисел R ; B y  - відповідне значення функції належності для параметра у, B y   0,1 . ~ 5 ~ Якщо функції належності первинних нечітких множин A,B  R задані в табличному вигляді, ~ ~ то попередньо перевіряють забезпечення властивостей нормальності (а, б) та опуклості (в, г) первинних нечітких множин, тобто перевіряють виконання умов: a) x  R :   A x   1 , тобто найбільше значення  A x  дорівнює 1; n n  ~ ~ ~ б) y  R :  B x   1 , тобто найбільше значення B x  дорівнює 1;  10 ~ в) x1, x2  R : A x1  1 x2   A x1 A x2  ,   0,1 ; ~ ~ ~ г) y1, y2  R : B y1  1 y2   B y1 B y2  ,   0,1 .  ~ ~ ~ Якщо умови а), б), в) і г) виконуються, то для заданої форми і параметрів функцій належності формують прямі (вертикальні) аналітичні моделі первинних нечітких множин у вигляді точних або апроксимованих аналітичних залежностей  A x  та B y  , які дозволяють для ~ 15      до нечітких ~ будь-яких значень х* та у* визначати ступені істинності їх належності A x* , B y* ~ множин A та B , відповідно. ~ ~  ~  На наступному етапі на основі прямих (вертикальних) аналітичних моделей  A x , B y  ~ ~ первинних нечітких множин A,B  R , формують інверсні (горизонтальні) аналітичні моделі ~ ~ 20 первинних нечітких множин A  a1, a2  , B  b1, b2  з використанням (фіг. 1) узагальнених горизонтальних -перерізів). При цьому -перерізом (множиною рівня ) нечіткої множини A R називають нечітку (але чітку - з точки зору умови ~  A x    ) підмножину A   R  , що містить елементи x R , ступінь належності яких до нечіткої ~ множини A не менша значення , тобто A   x  A x     ,   0,1 (фіг. 1). Відповідно,   ~  ~ 25  перерізом (множиною рівня ) нечіткої множини B  R  називають нечітку (але чітку - з точки ~ зору умови B y    ) підмножину B R , що містить елементи x R , ступінь належності яких ~ до множини B не менша значення , тобто B  x B y     ,   0,1 . Використовуючи інверсні   ~  ~  аналітичні моделі первинних нечітких множин A  a1, a2  , B  b1, b2  можна для 30 значення будь-якого рівня істинності  визначати у вигляді закритих інтервалів [а1(),а2()] та [b1(),b2()] діапазони існування носіїв {х, у} нечітких підмножин А, В. В подальшому вибирають необхідну операцію нечіткої арифметики   ,,*, / для первинних нечітких множин A,B  R , формують аналітичну інверсну модель C  c1, c2  ~ ~ функції належності результуючої нечіткої множини C  AB на основі інверсних моделей ~ ~ ~ A  a1, a2  та B  b1, b2  первинних нечітких множин, використовуючи при цьому 35 механізм реалізації відповідної операції нечіткої арифметики на основі застосування перерізів, зокрема: а) для операції додавання C  A B : ~ ~ ~ С=А(+)В=[а1(), a2()](+)[b1(),b2()]=[а1{)+b1(),a2()+b2()]=[c1(),c2()]; б) для операції віднімання C  AB : ~ ~ ~ 3 UA 68118 U С=А(-)В=[а1(),а2()](-)[b1(),b2()]=[а1()-b2(),а2()-b2()]=[с1(),с2()]; в) для операції множення C  A*B : ~ ~ ~ С=А(*)В=[а1(),а2()](*)[b1(),b2()]=[а1()*b1(),a2()*b2()]=[с1(),с2()]; а) для операції ділення C  A/ B : ~ ~ ~ С=А(/)В=[а1(),a2()](/)[b1(),b2()]=[а1()/b2(),а2()/b1()}=[с1(),с2()}; В подальшому формують пряму аналітичну модель C z    A  B z  функції належності 5 ~ ~ ~ результуючої нечіткої множини C  AB , необхідну для практичного використання в системах ~ ~ 10 15 ~ автоматичного керування в умовах невизначеності та в інтелектуальних системах обробки нечіткої інформації, у вигляді точної аналітичної або апроксимованої математичної залежності, + де z=x, x, y, zR . Цю процедуру розбивають на два етапи. На першому етапі розглядають рівняння лівої гілки функції належності результуючої нечіткої множини, яке отримують з її відповідної інверсної моделі, наприклад для операції ділення: с1()=а1()/b2(). Знаходять математичні залежності для всіх коренів 1i, і=1…І1 алгебраїчного рівняння а1()/b2()-с1()=0, де I1 - порядок алгебраїчного рівняння відносно змінної . Аналізують всі корені 1i, і=1…І1 і для формування прямої моделі лівої гілки залишають тільки * * корінь 1  f1 a, b, c1  , що задовольняє умову 1  0,1 .  В рівнянні  * * 1  f1a, b, c1  здійснюють формальні заміни c ()=z та 1  C z  . Пряму модель 1 ~ лівої гілки функції належності результуючої нечіткої множини C  AB формують при цьому у  ~  ~ ~ вигляді аналітичної залежності C z  AB z  f1 a, b, z , 0  z  z1* 1 . Якщо корені 1i, і=1…І1 ~ ~ 20 ~ знайти аналітичним шляхом досить складно або неможливо, то для лівої гілки функції належності результуючої нечіткої множини C формують математичну модель у вигляді ~ 25 апроксимуючої аналітичної залежності, наприклад у вигляді поліноміальної моделі відповідного порядку. На другому етапі розглядають рівняння правої гілки функції належності результуючої нечіткої множини, яке отримують з її відповідної інверсної моделі, наприклад для операції множення: с2()=а2()*b2(). Знаходять математичні залежності для всіх коренів 2і, і=1…І2 алгебраїчного рівняння а2()*b2()-с2()=0, де I2 – порядок алгебраїчного рівняння відносно змінної . Аналізують всі корені а2i, і=1…І2 і для формування прямої моделі правої гілки залишають тільки корінь *  f2 a, b, c 2   , що задовольняє умову *  0,1 . 2 2 В рівнянні * 2      f2 a, b, c 2   здійснюють формальні заміни c2()=z та *  C z . Пряму модель 2 ~ 30 правої гілки функції належності результуючої нечіткої множини C  AB формують при цьому у  ~  ~ ~ вигляді аналітичної залежності C z  AB z  f2 a, b, z , z *2 1  z   . Якщо корені 2і, і=1…І2 ~ ~ ~ знайти аналітичним шляхом досить складно або неможливо, то для правої гілки функції належності результуючої нечіткої множини C формують математичну модель у вигляді ~ 35 апроксимуючої аналітичної залежності, наприклад у вигляді поліноміальної моделі відповідного порядку. Повну пряму аналітичну модель функції належності результуючої нечіткої множини C  AB в остаточному вигляді формують наступним чином: ~ ~ ~      f a, b, z , 0  z  z * 1 1  1  , C z   1 z  z * 1  z * 1 , 1 2 ~   f a, b, z , z *2 1  z   2 де C z * 1  C z * 1  1 визначає  ~  1  ~  2   ядро результуючої нечіткої множини C, тобто ~ core C  z : C z  1 z  R . , ~ 40 ~ В подальшому здійснюють ряд {1, 2,…,j, …,J-1,J} тестових випробувань для перевірки адекватності синтезованих моделей, для чого задають ряд тестових значень -рівнів в межах інтервалу від нуля до одиниці, тобто j, j=1…J, j[0, 1]. Почергово для всіх тестових значень j, j=1…J, j[0, 1] за інверсною моделлю C j  c1 j , c 2  j  функції належності результуючої  4  UA 68118 U нечіткої множини C  AB визначають у вигляді закритих інтервалів c1 j , c 2  j  діапазони ~   ~ ~ існування носіїв sup p C j нечітких підмножин C j зі ступенем істинності , що є не меншим від вибраного на відповідному j-му кроці тестування -рівня, тобто    j z  c1 j , c 2  j  . Для     сформованих граничних значень 5 відповідних носіїв ~ кожного з закритих інтервалів ~ c1 j , c2  j    нечітких підмножин C визначають два значення ступенів z  f a, b, z  f a, b, c  , j  1, J та  z     z  f a, b, z  f a, b, c   , sup p C j істинності C z  AB ~ c1  j , c 2  j j 1 1 1 j AB C ~ ~ 2 ~ 2 2 j j   , J відповідно до лівої і правої гілок функції належності при використанні синтезованої 1 прямої аналітичної моделі C z  результуючої нечіткої множини C  AB (фіг. 2). ~ ~ ~ Попередньо задають допустимі порогові значення похибок 10 ~  , а в подальшому контролюють величини розугоджень між отриманими значеннями ступенів істинності f1 a, b, c1 j  , f2 a, b, c 2  j  , j   , J для границь закритих інтервалів та початковими тестовими 1     значеннями j, j=1…J, j[0, 1] відповідних -рівнів. У випадку перевищення контрольованими похибками заданих порогових значень L  f1 a, b, c1  j   j   (для лівої гілки функції       належності), R  f2 a, b, c2  j   j   (для лівої гілки функції належності) здійснюють корекцію 15 синтезованої прямої аналітичної моделі C z  функції належності результуючої нечіткої ~ множини C  AB шляхом уточнення аналітичних розв'язків або шляхом корекції параметрів ~ ~ ~ чи структури апроксимуючих моделей для зменшення апроксимаційних похибок. Процедури тестових випробувань прямої моделі результуючої нечіткої множини C  AB ~ 20 25 ~ ~ та її коригування повторюють в цикловому режимі і завершують їх при умові, що всі похибки (розугодження) знаходяться в межах допустимих порогових значень, тобто f1 a, b, c1  j   j   , f2 a, b, c2  j   j   .       Позитивний ефект проявляється в тому, що в порівнянні з прототипом даний спосіб забезпечує підвищення рівня адекватності синтезованих інверсних та прямих аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої арифметики, а також підвищення надійності пристроїв, що реалізують відповідні операції нечіткої арифметики на основі запропонованого способу формування моделей результуючих нечітких множин. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 30 35 40 45 50 Спосіб формування аналітичних моделей результуючих нечітких множин при реалізації операцій нечіткої арифметики, згідно з яким послідовно вибирають форму функцій належності та параметри первинних нечітких множин, над якими планують здійснення однієї з операцій нечіткої арифметики, зокрема додавання, віднімання, множення або ділення, формують прямі (вертикальні) аналітичні моделі первинних нечітких множин, на основі яких формують інверсні (горизонтальні) аналітичні моделі первинних нечітких множин з використанням узагальнених горизонтальних -перерізів, вибирають необхідну операцію нечіткої арифметики для первинних нечітких множин, формують аналітичну інверсну модель функції належності результуючої нечіткої множини на основі інверсних моделей первинних нечітких множин, використовуючи при цьому механізм реалізації відповідної операції нечіткої арифметики на основі застосування перерізів, а в подальшому формують пряму аналітичну модель функції належності результуючої нечіткої множини у вигляді точної аналітичної або апроксимованої математичної залежності, який відрізняється тим, що попередньо перевіряють забезпечення властивостей нормальності та опуклості первинних нечітких множин, здійснюють ряд тестових випробувань для перевірки адекватності синтезованих моделей, для чого задають ряд тестових значень рівнів в межах інтервалу від нуля до одиниці, для яких за інверсною моделлю функції належності результуючої нечіткої множини визначають у вигляді закритих інтервалів діапазони існування носіїв нечітких підмножин зі ступенем істинності, що є не меншим від вибраного на відповідному кроці тестування -рівня, для сформованих граничних значень кожного з закритих інтервалів відповідних носіїв нечітких підмножин визначають два значення ступенів істинності відповідно до лівої і правої гілок функції належності при використанні синтезованої прямої 5 UA 68118 U 5 аналітичної моделі результуючої нечіткої множини, задають допустимі порогові значення похибок, а в подальшому контролюють величини розузгоджень між отриманими значеннями ступенів істинності для границь закритих інтервалів та початковими тестовими значеннями відповідних -рівнів, у випадку перевищення контрольованими похибками попередньо заданих порогових значень здійснюють корекцію синтезованої прямої аналітичної моделі функції належності результуючої нечіткої множини і повторюють процедуру її тестових випробувань, які завершують при умові, що всі похибки знаходяться в межах допустимих порогових значень. 6 UA 68118 U Комп’ютерна верстка Г. Паяльніков Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 7