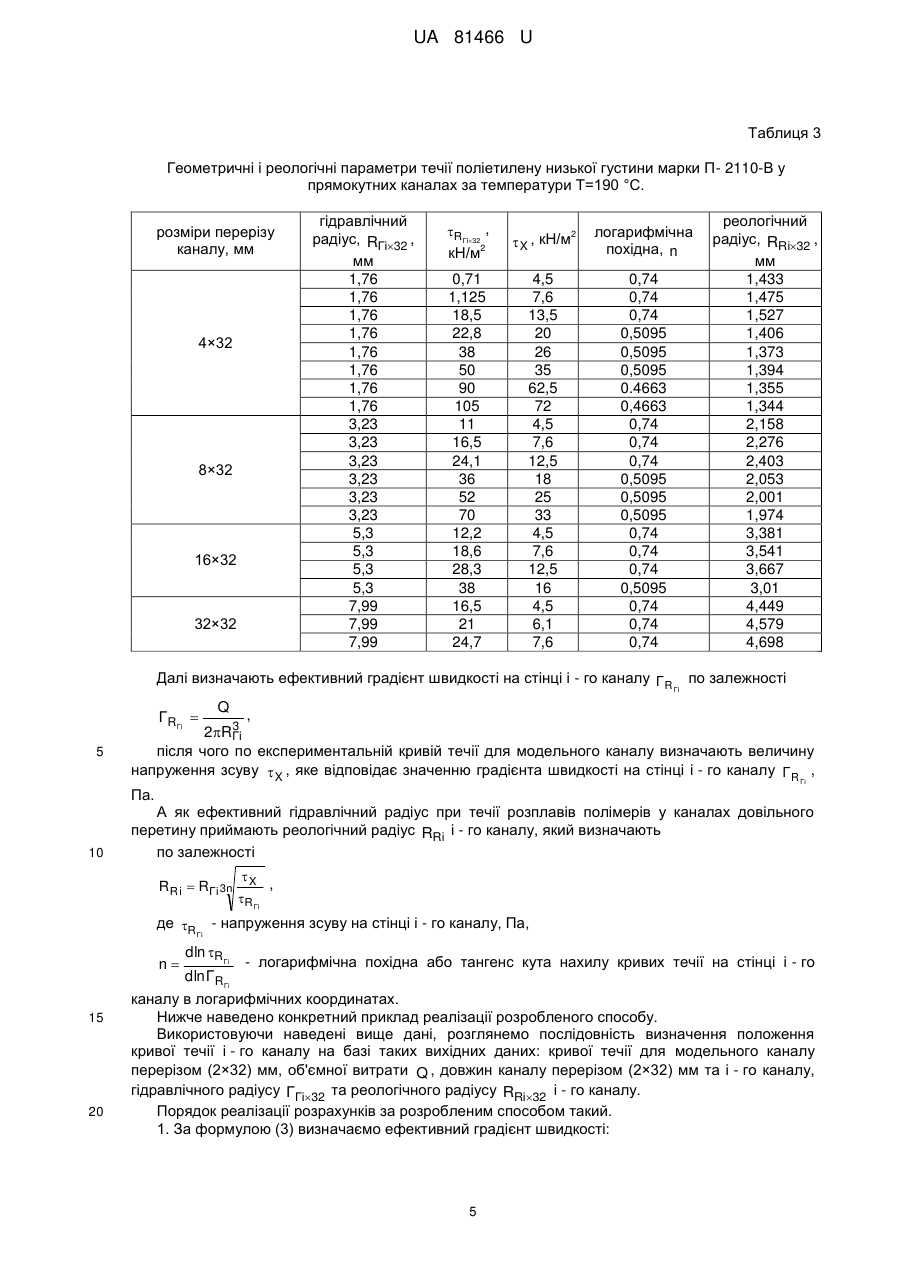
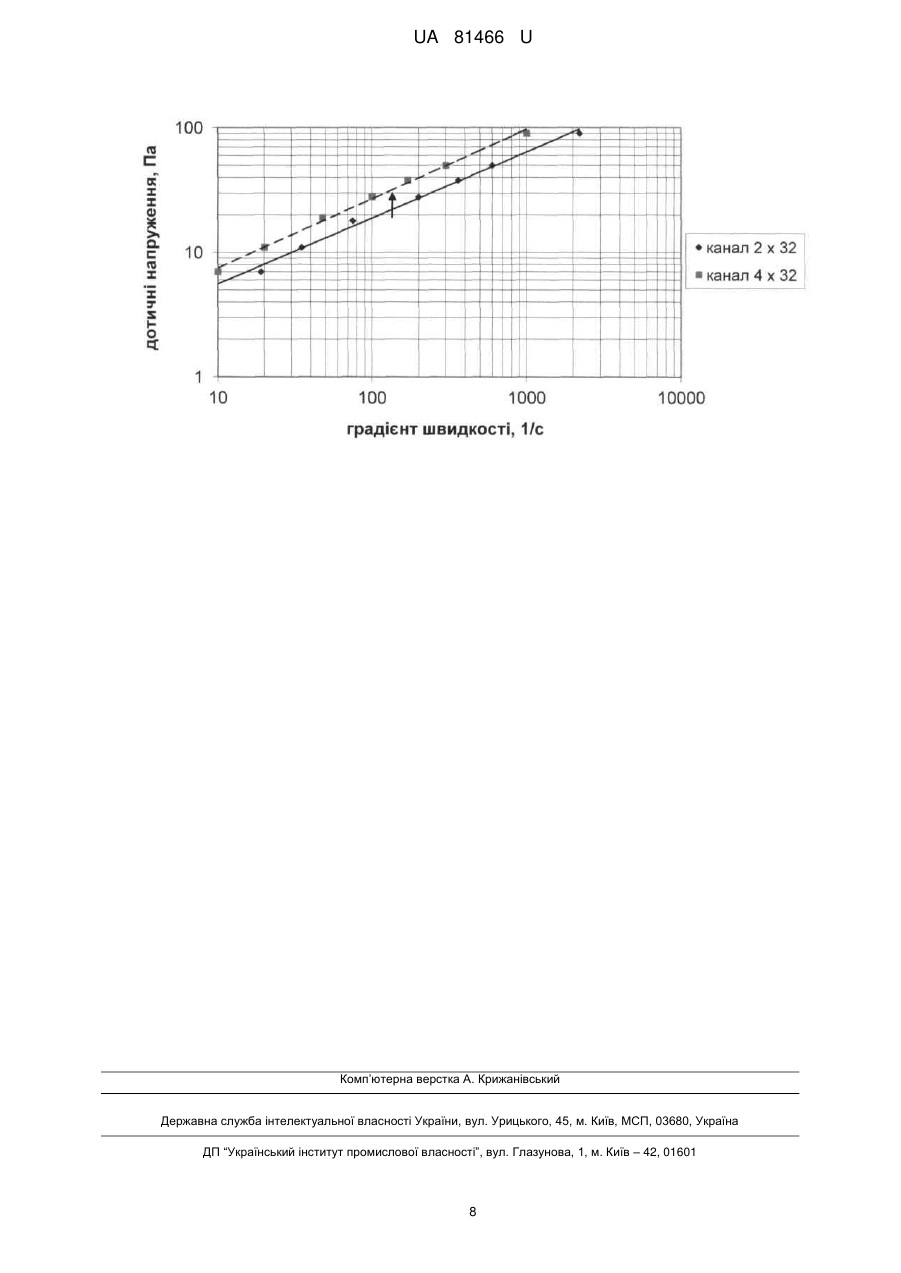
Спосіб визначення ефективного гідравлічного радіуса при течії розплавів полімерів у каналах довільного перетину
Номер патенту: 81466
Опубліковано: 25.06.2013
Автори: Борщик Сергій Олександрович, Коваленко Ксенія Геннадіївна, Радич Юлія Володимирівна, Колосов Олександр Євгенович, Пристайлов Сергій Олегович, Сокольський Олександр Леонідович, Сідоров Дмитро Едуардович, Романченко Марія Анатоліївна, Кушнір Михайло Сергійович, Куриленко Валерій Миколайович, Колосова Олена Петрівна, Сівецький Володимир Іванович, Педченко Анатолій Юрійович
Формула / Реферат
Спосіб визначення ефективного гідравлічного радіуса при течії розплавів полімерів у каналах довільного перетину, що полягає у визначенні геометричних параметрів каналів, а саме їх довжини і поперечного перерізу, і реологічних властивостей розплаву полімеру у вигляді динамічної в'язкості, з наступною побудовою розрахунково-експериментальної кривої течії розплаву полімеру в досліджуваному каналі заданої геометрії, який відрізняється тим, що здійснюють побудову експериментальної кривої течії досліджуваного розплаву полімеру в модельному каналі, наприклад, прямокутної форми з розмірами перерізу (2×32) мм, задають об'ємну витрату ![]() течії розплаву полімеру в довільному і-му каналі, визначають гідравлічний радіус
течії розплаву полімеру в довільному і-му каналі, визначають гідравлічний радіус ![]() і-го каналу по залежності
і-го каналу по залежності
![]() ,
,
де ![]() - площа нормального перерізу і-го каналу, м2,
- площа нормального перерізу і-го каналу, м2,
![]() - змочений периметр, м,
- змочений периметр, м,
![]() - гідравлічний радіус, м,
- гідравлічний радіус, м,
визначають ефективний градієнт швидкості на стінці і-го каналу ![]() по залежності
по залежності
![]() ,
,
після цього по експериментальній кривій течії для модельного каналу визначають величину напруження зсуву ![]() , яке відповідає значенню градієнта швидкості на стінці і-го каналу
, яке відповідає значенню градієнта швидкості на стінці і-го каналу ![]() , а як ефективний гідравлічний радіус при течії розплавів полімерів у каналах довільного перетину приймають реологічний радіус
, а як ефективний гідравлічний радіус при течії розплавів полімерів у каналах довільного перетину приймають реологічний радіус ![]() і-го каналу, який визначають по залежності
і-го каналу, який визначають по залежності
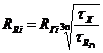 ,
,
де ![]() - напруження зсуву на стінці і-го каналу, Па,
- напруження зсуву на стінці і-го каналу, Па,
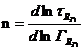 - логарифмічна похідна або тангенс кута нахилу кривих течії на стінці і-го каналу в логарифмічних координатах.
- логарифмічна похідна або тангенс кута нахилу кривих течії на стінці і-го каналу в логарифмічних координатах.
Текст
Реферат: Спосіб визначення ефективного гідравлічного радіуса при течії розплавів полімерів у каналах довільного перетину полягає у визначенні геометричних параметрів каналів, а саме їх довжини і поперечного перерізу, і реологічних властивостей розплаву полімеру у вигляді динамічної в'язкості, з наступною побудовою розрахунково-експериментальної кривої течії розплаву полімеру в досліджуваному каналі заданої геометрії. Здійснюють побудову експериментальної кривої течії досліджуваного розплаву полімеру в модельному каналі, наприклад, прямокутної форми з розмірами перерізу (2×32) мм, задають об'ємну витрату течії розплаву полімеру в довільному і-му каналі, визначають гідравлічний радіус і-го каналу. UA 81466 U (12) UA 81466 U UA 81466 U 5 10 Корисна модель належить до способів визначення ефективного гідравлічного радіуса при течії розплавів полімерів у каналах довільного перетину, і може бути використана в дослідженні реологічних властивостей розплавів полімерів. Відомий спосіб визначення ефективного гідравлічного радіуса при течії розчинів термореактивних полімерів у пористих виробах у вигляді циліндричних каналів, що включає заповнення полімерною рідиною еталонного виробу, приведення його в контакт із досліджуваним зразком, при цьому вимірюють радіус циліндричного наскрізного капіляра, герметизують після заповнення рідиною вільний кінець капіляра, вимірюють довжину стовпчика рідини у капілярі до приведення в контакт з вимірюваним виробом і після контакту у момент досягнення капілярної рівноваги визначають ефективний радіус пор із співвідношення Pа R/[1 - ( о - проп)/( о - ост )] , де - коефіцієнт поверхневого натягнення змочувальної рідини, Н/м; Pа - атмосферний тиск, Па; R - радіус капіляра, м; - крайовий кут змочування, , проп - довжина стовпчика 15 20 25 30 35 40 45 рідини до приведення у контакт з вимірюваним виробом, м; ост - довжина стовпчика рідини після встановлення капілярної рівноваги, м; о - довжина капіляра, м [1]. Недоліком способу аналога є його неможливість для використання при визначенні ефективного гідравлічного радіуса при течії розплавів полімерів у каналах довільного перерізу. Як найбільш близький аналог вибраний спосіб визначення ефективного гідравлічного радіуса пористого середовища [2]. Згідно з цим способом, пористе середовище у вигляді армуючих наповнювачів з регулярною структурою просочують рідиною, будують криві розподілу пор за розмірами, а також експериментальні кінетичні криві просочування, а саме залежність висоти просочування або підйому просочувальної рідини уздовж волокнистого наповнювача h у часі t , а шуканий ефективний радіус пор rеф знаходять розрахунковим шляхом у залежності від характеристик структури пористого середовища і реологічних властивостей просочувальної рідини. Недоліком способу найближчого аналога є його неможливість для використання при визначенні ефективного гідравлічного радіуса при течії розплавів полімерів у каналах довільного перетину в тих випадках, коли внаслідок пристінних ефектів криві течії, отримані на каналах різних перерізів, не співпадають між собою, тобто є неінваріантними відносно гідравлічного радіуса. В основу корисної моделі поставлена задача підвищення достовірності способу визначення ефективного гідравлічного радіуса при течії розплавів полімерів у каналах довільного перерізу шляхом експериментально-теоретичного врахування неінваріантності залежності дотичних напружень на стінках каналів, в яких протікає розплав полімеру, від градієнта швидкості розплаву. Поставлена задача вирішується тим, що у способі визначення ефективного гідравлічного радіуса при течії розплавів полімерів у каналах довільного перетину, що полягає у визначенні геометричних параметрів каналів, а саме їх довжини і поперечного перерізу, і реологічних властивостей розплаву полімеру у вигляді динамічної в'язкості, з наступною побудовою розрахунково-експериментальної кривої течії розплаву полімеру в досліджуваному каналі заданої геометрії, новим є те, що, здійснюють побудову експериментальної кривої течії досліджуваного розплаву полімеру в модельному каналі, наприклад, прямокутної форми з розмірами перерізу (2×32) мм, задають об'ємну витрату Q течії розплаву полімеру в довільному і-му каналі, визначають гідравлічний радіус RГі і-го каналу по залежності S, 2 де S - площа нормального перерізу і-го каналу, м , - змочений периметр, м, RГі RГі - гідравлічний радіус, м, визначають ефективний градієнт швидкості на стінці і-го каналу Г R по залежності Гі 50 Г R Гі S , 3 2RГі після цього по експериментальній кривій течії для модельного каналу визначають величину напруження зсуву X , яке відповідає значенню градієнта швидкості на стінці і-го каналу Г R , а Гі 1 UA 81466 U як ефективний гідравлічний радіус при течії розплавів полімерів у каналах довільного перетину приймають реологічний радіус RRi і-го каналу, який визначають по залежності RRi RГі 3n X , R Гі де R - напруження зсуву на стінці і-го каналу, Па, Гі 5 10 15 n d ln R Гі - логарифмічна похідна або тангенс кута нахилу кривих течії на стінці і-го каналу d ln Г R Гі в логарифмічних координатах. Перераховані ознаки способу складають суть корисної моделі. Наявність причинно-наслідкового зв'язку між сукупністю істотних ознак корисної моделі і технічним результатом, що досягається, полягає в наступному. Питання про використання поняття гідравлічного радіуса як адекватного способу переходу від циліндричних каналів некруглого поперечного перерізу до круглих каналів при течії неньютонівських рідин, зокрема розплавів полімерів, являє значний практичний інтерес у зв'язку із розповсюдженням таких каналів у обладнанні для отримання виробів із полімерів та устаткуванні для інших процесів хімічної технології. При гідравлічному розрахунку некруглих каналів гідравлічний опір циліндричних або призматичних каналів складного профілю визначають шляхом порівняння опору цих каналів з еквівалентним їм за опором каналом круглого поперечного перерізу, у якому за радіус приймається "гідравлічний радіус" RГ [4,7]: RГ S, (1) 20 2 де S - площа нормального перерізу каналу, м ; - змочений периметр, м. Якщо використати поняття гідравлічного радіуса, то середнє за периметром напруження тертя або, інакше, напруження зсуву на стінці каналу 25 R 30 35 P R Г , L (2) де P - перепад тиску на ділянці каналу, Па; L - довжина ділянки каналу; R - напруження зсуву, Па. Рівняння (2) можна використовувати для будь-яких суцільних середовищ, які рухаються у циліндричних каналах, зокрема, при русі неньютонівських рідин [7]. Недоліком способу [7] є те, що при використанні гідравлічного радіуса RГ необхідно враховувати, що цей спосіб має сенс тільки у тому випадку, якщо у каналів, які порівнюють за опором, перерізи геометрично близькі один до одного. У реології неньютонівських рідин величина R використовується для побудови кривої течії, яка є графічним виразом залежності напруження зсуву на стінці каналу від градієнта швидкості розплаву на стінці каналу (так званого ефективного градієнта швидкості), тобто R (ГR ) . При цьому величина ефективного градієнта швидкості Гц в каналі може бути обчислена за формулою 40 ГR Q 2Rі2 , (3) 3 45 де Q - об'ємна витрата розплаву в каналі, м /с. Було експериментально досліджено течію неньютонівської рідини у прямокутних каналах розмірами (2×32) мм, (4×32) мм, (8×32) мм, (16×32) мм та (32×32) мм. Величини гідравлічного радіуса RГ були визначені за формулою (1). 2 UA 81466 U 5 10 15 20 Для дослідження був використаний модифікований віскозиметр сталих швидкостей, який дозволяє реалізувати усталений потік розплавів полімерів у широкому діапазоні зміни швидкостей течії у каналах із геометрією та розмірами, які фактично використовуються у конструкціях головок черв'ячних машин [5]. Для віскозиметричних досліджень зазвичай використовують круглі канали. Якщо неньютонівська рідина не виявляє пристінних ефектів, то криві течії, які були отримані на круглих каналах різних діаметрів, накладаються одна на одну і практично є інваріантними відносно діаметра каналу. З цієї точки зору, використання поняття гідравлічного радіуса RГ для розрахунку каналів із перерізом некруглої форми повинно було б забезпечити інваріантність їх реологічних характеристик відносно величини гідравлічного радіуса каналу. Перевірка цього положення була здійснена для типової неньютонівської рідини, зокрема, розплаву поліетилену низької об'ємної густини марки П-2010-В за температур 150 °C та 190 °C. Розплав цього поліетилену є свого роду еталонним матеріалом, особливості реологічної поведінки якого достатньо відомі та описані у літературі [5, 6]. Він поводить себе як типова неньютонівська рідина, що підкоряється ступеневому закону. Криві течії розплаву цього полімеру інваріантні відносно діаметра каналу. Для нього не характерна аномальна реологічна поведінка на межі зі стінкою каналу або в об'ємних шарах потоку. У той же час, для нього установлена неоднорідність розподілу напружень у потоці розплаву при його течії у прямокутному каналі [9]. За формулами (2) і (3) для вищевказаних каналів були визначені криві течії. Слід відмітити, що у реологічному аспекті [10] величина дотичного напруження, розрахована з використанням гідравлічного радіуса R повинна бути однозначною функцією ефективного градієнта Г 25 швидкості, розрахованого з використанням гідравлічного радіуса ГR . І цю залежність можна Г застосувати до течії рідини крізь будь-який канал будь-якого перерізу [8]. Отримані криві течії мають яскраво виражену неінваріантність відносно гідравлічного радіуса каналу RГ , яку неможливо пояснити особливостями поведінки еталонного матеріалу у пристінному шарі або у об'ємних шарах потоку. Тобто поняття гідравлічного радіуса RГ , не дає змоги отримати для каналів довільної, наприклад прямокутної форми, величин R і ГR , які б Г Г 30 забезпечили інваріантність кривих течії відносно геометричних розмірів каналів, тобто R не є Г однозначною функцією ГR . Г Розв'язання цієї задачі запропоновано у роботі [10] і полягає у визначенні геометричного параметра каналу, який би також залежав і від реологічних характеристик полімеру. Таким параметром може бути радіус каналу RR , який умовно можна назвати реологічним. 35 Реологічний радіус RRi32 для і-го каналу можна визначити із рівняння: RRi32 RГi32 3n 40 45 X R Гі32 (4) де RГi32 - гідравлічний радіус і - го каналу, м; dln Ri32 - логарифмічна похідна або тангенс кута нахилу логарифмічних кривих n dln ГRi32 напруження зсуву на стінці каналу від ефективного градієнта швидкості; X - напруження зсуву, яке відповідає ГRi32 на кривій течії модельного каналу перерізом (2×32) мм, Па; RГі32 - напруження зсуву і - го каналу, Па. Розглянемо відхилення отриманих з використанням гідравлічного радіуса кривих течії від кривої течії у модельному каналі перерізом (2×32) мм, яка є еталонною віскозиметричною кривою течії у плоскій щілині. Значення відносної похибки розташування кривих течії за напруженнями зсуву на стінці каналу при сталих значеннях ефективного градієнта швидкості для каналів перерізами (4×32) мм, (8×32) мм, (16×32) мм та (32×32) мм при температурі 190 °C наведені у табл.1. 50 3 UA 81466 U Таблиця 1 Значення відносної похибки розташування кривих течії за напруженнями зсуву, %. розміри каналу, мм 4×32 8×32 16×32 32×32 10 55,55 144,44 172,22 261,11 ефективний градієнт швидкості, 1/с 20 50 100 200 51,31 35,71 40 41,37 117,10 97,14 105 106,98 143,42 132,14 228,94 1000 47,54 Значення відносної похибки розташування кривих течії за ефективного градієнта швидкості при сталих значеннях напружень зсуву на стінці каналу наведені у табл. 2. 5 Таблиця 2 Значення відносної похибки розташування кривих течії за ефективного градієнта швидкості, %. напруження зсуву на стінці каналу X , яке відповідає ГRi32 течії каналу 2 канал перерізом (2×32) мм Н/м 50 100 200 300 500 4×32 46,09 46,67 45,5 45,45 50 8×32 71,30 70 72 73,18 75,83 16×32 76,52 76 77,5 80 32×32 85,22 84,33 86 10 15 20 25 на кривій 1000 54,54 Із наведених у табл. 1 і табл. 2 даних витікає, що відносні похибки кривих течії розплаву поліетилену низької густини марки П- 2010-В у прямокутних каналах від еталонної віскозиметричної кривої течії цього полімеру не є сталими величинами. Найбільш яскраво ця непостійність виражена у значеннях похибки положення за напруженнями зсуву на стінці каналу (див. табл. 2). Однак, похибки за ефективного градієнта швидкості також виявляють відхилення, які відображаються у збільшенні значень похибки зі збільшенням напруження зсуву на стінці каналу. У табл. 3 проведено порівняння гідравлічних радіусів RГi32 і реологічних радіусів RRi32 для прямокутних каналів. Із табл. 3 випливає, що для кожного типорозміру прямокутного каналу гідравлічний радіус RГi32 перевищує реологічний радіус RRi32 . Спосіб ілюструється кресленням, де зображена послідовність побудови для визначення дійсної кривої течії поліетилену низької густини марки П- 2010-В у прямокутному каналі перерізом 4×32 мм на базі даних, отриманих для модельного каналу перерізом (2×32) мм за температури Т=190 °C. Спосіб реалізується наступним чином. Здійснюють побудову експериментальної кривої течії досліджуваного розплаву полімеру в модельному каналі, наприклад, прямокутної форми з розмірами перерізу (2×32) мм. Задають об'ємну витрату Q течії розплаву полімеру в довільному і - му каналі. Після цього визначають гідравлічний радіус RГi і - го каналу по залежності S 2 де S - площа нормального перерізу і - го каналу, м , - змочений периметр, м, RГi RГi - гідравлічний радіус, м. 30 4 UA 81466 U Таблиця 3 Геометричні і реологічні параметри течії поліетилену низької густини марки П- 2110-В у прямокутних каналах за температури Т=190 °C. розміри перерізу каналу, мм 4×32 8×32 16×32 32×32 гідравлічний радіус, RГi32 , мм 1,76 1,76 1,76 1,76 1,76 1,76 1,76 1,76 3,23 3,23 3,23 3,23 3,23 3,23 5,3 5,3 5,3 5,3 7,99 7,99 7,99 RГі32 , 2 кН/м X , кН/м 0,71 1,125 18,5 22,8 38 50 90 105 11 16,5 24,1 36 52 70 12,2 18,6 28,3 38 16,5 21 24,7 4,5 7,6 13,5 20 26 35 62,5 72 4,5 7,6 12,5 18 25 33 4,5 7,6 12,5 16 4,5 6,1 7,6 2 логарифмічна похідна, n 0,74 0,74 0,74 0,5095 0,5095 0,5095 0.4663 0,4663 0,74 0,74 0,74 0,5095 0,5095 0,5095 0,74 0,74 0,74 0,5095 0,74 0,74 0,74 реологічний радіус, RRi32 , мм 1,433 1,475 1,527 1,406 1,373 1,394 1,355 1,344 2,158 2,276 2,403 2,053 2,001 1,974 3,381 3,541 3,667 3,01 4,449 4,579 4,698 Далі визначають ефективний градієнт швидкості на стінці і - го каналу Г R по залежності Гi Г R Гі 5 Q , 3 2RГі після чого по експериментальній кривій течії для модельного каналу визначають величину напруження зсуву X , яке відповідає значенню градієнта швидкості на стінці і - го каналу Г R , Гi Па. 10 А як ефективний гідравлічний радіус при течії розплавів полімерів у каналах довільного перетину приймають реологічний радіус RRi і - го каналу, який визначають по залежності RRi RГi 3n X , R Гі де R - напруження зсуву на стінці і - го каналу, Па, Гі n 15 20 d ln R Гі d ln Г R Гі - логарифмічна похідна або тангенс кута нахилу кривих течії на стінці і - го каналу в логарифмічних координатах. Нижче наведено конкретний приклад реалізації розробленого способу. Використовуючи наведені вище дані, розглянемо послідовність визначення положення кривої течії і - го каналу на базі таких вихідних даних: кривої течії для модельного каналу перерізом (2×32) мм, об'ємної витрати Q , довжин каналу перерізом (2×32) мм та і - го каналу, гідравлічного радіусу ГГі32 та реологічного радіусу RRі32 і - го каналу. Порядок реалізації розрахунків за розробленим способом такий. 1. За формулою (3) визначаємо ефективний градієнт швидкості: 5 UA 81466 U ГRГі32 Q . 3 2RГі32 2. По кривій течії для модельного каналу перерізом (2×32) мм визначаємо величину напруження зсуву X . 5 3. Враховуючи, що R RRі32 , використовуємо рівняння (4) для визначення напруження Гі32 зсуву на стінці і - го каналу: 3n R RГі32 X Гі32 R Rі32 4. За допомогою кривої течії для модельного каналу (2×32) мм знаходимо величину Г R Rі32 для і - го каналу і перевіряємо її величину за формулою роботи [7]: Г R Rі32 Г R Гі32 n 10 R Гі32 . X 5. Шукану точку кривої течії і - го каналу знаходимо як точка перетину прямих, одна з яких перпендикулярна до осі ефективних градієнтів швидкості у точці Г R , а друга пряма Гі32 перпендикулярна до осі напружень зсуву у точці R (див. фіг.). Гі32 В табл. 4 наведені дані для визначення кривої течії для каналу перерізом 4×32 мм. Таблиця 4 Параметри течії поліетилену низької густини марки П- 2010-В у каналі перерізом (4×32) мм за температури Т=190 °C. гідравлічний реологічний радіус, радіус, RГ 432 , RR432 , мм мм 1,76 1,433 1,76 1,475 1,76 1,527 1,76 1,406 1,76 1,373 1,76 1,394 1,76 1,355 1,76 1,344 R Г 432 , 2 кН/м X , кН/м 7Д 11,25 18,5 28,2 38 50 90 105 4,5 7,6 13,5 20 26 35 62,5 72 2 Г R Г 432 , с 10,0 20,0 47,5 100 170 300 1000 1375 -1 ГR R 432 , с -1 18,54 34,0 72,66 196,3 358,3 606,0 2190 3102,14 логарифмічна похідна, n 0,74 0,74 0,74 0,5095 0,5095 0,5095 0,4663 0,4663 15 Було встановлено, що розрахунки параметрів течії з використанням поняття гідравлічного радіуса може призвести до значних відхилень від реальної картини течії полімерної рідини. Поняття гідравлічного радіуса каналів некруглого перерізу при течії неньютонівської рідини не дає змоги отримати величини R та ГR , які забезпечили б інваріантність кривих течії відносно Г 20 25 30 Г геометричних розмірів каналу. Тоді як використання за розробленим способом поняття реологічного радіуса дає змогу побудови кривих течії полімерів в каналах довільного перерізу за наявності таких експериментальних даних хоча б для одного модельного каналу. Джерела інформації: 1. Прохоренко ПП., Довгялло Г.И., Корнев А.П., Мигун Н.П. Способ измерения эффективного радиуса пор в пористых изделиях. Авторское свидетельство СССР № 1742681. МКИ G 01 N 15/08. Опубл. в Б.И. № 23, 1992 г. 2. Чизмакджев Ю.А., Маркин B.C., Тарасевич М.Р., Чирков Ю.Г. Макрокинетика процессов в пористых средах. - М.: Наука, 1971.- 364 с. 3. Воюцкий С.С. Физико - химические основы пропитывания и импрегнирования волокнистых материалов дисперсиями полимеров. - Л.: Химия, 1969.- 336 с. 4. Емцев Б.Т. Техническая гидромеханика: учебник для вузов по специальности "Гидравлические машины и средства автоматики". - М.: Машиностроение, 1978.- 463 с. 6 UA 81466 U 5 10 5. Жданов Ю.А. Исследование течения расплавов полимеров в каналах головок червячных машин. Автореферат диссертации, представленной на соискание ученой степени канд. тех. наук - К.: 1969. - С. 3 - 24. 6. Чернобыльский И.И., Рябинин Д.Д., Жданов Ю.А., Иванова Л.А. Исследование течения полиэтилена низкой плотности в прямоугольных цилиндрических каналах// Химическая технология.- 1973. - № 5 (71). - С. 15 - 18. 7. Лойцянский Л.Г. Механика жидкости и газа. 6-е изд. - М.: Наука, 1988.- 840 с. 8. Мак - Келви Д.М. Переработка полимеров. - М.: Химия, 1965.- 443 с. 9. Яхно О.М., Рябинин Д.Д., Ищенко Л.А., Лотоцкий Ю.В. Распределение напряжений в потоке расплава полимера формующего канала//Химическая технология.- 1979. - № 4(106).-С. 40 - 42. 10. Рябінін Д.Д., Мотін A.M. Про реологічний аспект використання поняття гідравлічного радіуса.//Вестник Национального технического университета Украины "Киевский политехнический институт". Сер. Машиностроение. - Вып. 41.- 2001. - С. 55 - 59. 15 ФОРМУЛА КОРИСНОЇ МОДЕЛІ 20 25 Спосіб визначення ефективного гідравлічного радіуса при течії розплавів полімерів у каналах довільного перетину, що полягає у визначенні геометричних параметрів каналів, а саме їх довжини і поперечного перерізу, і реологічних властивостей розплаву полімеру у вигляді динамічної в'язкості, з наступною побудовою розрахунково-експериментальної кривої течії розплаву полімеру в досліджуваному каналі заданої геометрії, який відрізняється тим, що здійснюють побудову експериментальної кривої течії досліджуваного розплаву полімеру в модельному каналі, наприклад, прямокутної форми з розмірами перерізу (2×32) мм, задають об'ємну витрату Q течії розплаву полімеру в довільному і-му каналі, визначають гідравлічний радіус RГі і-го каналу по залежності S , 2 де S - площа нормального перерізу і-го каналу, м , - змочений периметр, м, RГі 30 RГі - гідравлічний радіус, м, визначають ефективний градієнт швидкості на стінці і-го каналу RГі по залежності ГRГі S , 3 2RГі після цього по експериментальній кривій течії для модельного каналу визначають величину напруження зсуву X , яке відповідає значенню градієнта швидкості на стінці і-го каналу Г R Гі , а 35 як ефективний гідравлічний радіус при течії розплавів полімерів у каналах довільного перетину приймають реологічний радіус RRi і-го каналу, який визначають по залежності RRi RГі 3n X , R Гі де RГі - напруження зсуву на стінці і-го каналу, Па, n 40 d ln R Гі d ln ГR Гі - логарифмічна похідна або тангенс кута нахилу кривих течії на стінці і-го каналу в логарифмічних координатах. 7 UA 81466 U Комп’ютерна верстка А. Крижанівський Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 8
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determination of effective hydraulic radius at flow of polymer melts in channels with arbitrary cross sections
Автори англійськоюKolosov Oleksandr Yevhenovych, Sivetskyi Volodymyr Ivanovych, Sidorov Dmytro Eduardovych, Sokolskyi Oleksandr Leonidovych, Prystailov Serhii Olehovych, Borschyk Serhii Oleksandrovych, Kolosova Olena Petrivna, Kushnir Mykhailo Serhiiovych, Kovalenko Ksenia Hennadiivna, Radich Yulia Volodymyrivna, Kurylenko Valerii Mykolaiovych, Pedchenko Anatolii Yuriiovych, Romanchenko Maria Anatoliivna
Назва патенту російськоюСпособ определения эффективного гидравлического радиуса при течении расплавов полимеров в каналах произвольного сечения
Автори російськоюКолосов Александр Евгеньевич, Сивецкий Владимир Иванович, Сидоров Дмитрий Эдуардович, Сокольский Александр Леонидович, Пристайлов Сергей Олегович, Борщик Сергей Александрович, Колосова Елена Петровна, Кушнир Михаил Сергеевич, Коваленко Ксения Геннадиевна, Радич Юлия Владимировна, Куриленко Валерий Николаевич, Педченко Анатолий Юрьевич, Романченко Мария Анатолиевна
МПК / Мітки
МПК: G01N 11/00
Мітки: спосіб, довільного, гідравлічного, перетину, каналах, визначення, розплавів, течії, полімерів, ефективного, радіуса
Код посилання
<a href="https://ua.patents.su/10-81466-sposib-viznachennya-efektivnogo-gidravlichnogo-radiusa-pri-techi-rozplaviv-polimeriv-u-kanalakh-dovilnogo-peretinu.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення ефективного гідравлічного радіуса при течії розплавів полімерів у каналах довільного перетину</a>
Попередній патент: Спосіб визначення коефіцієнта тертя ковзання для пари “термопластичний полімер-сталь” у залежності від температури
Наступний патент: Спосіб визначення реологічних параметрів течії розплавів термопластичних полімерів в каналах довільної геометрії
Випадковий патент: Спосіб моделювання пародонтиту з ураженням сполучної тканини пародонта