Цифровий інтегро-арифметичний пристрій
Номер патенту: 91258
Опубліковано: 25.06.2014
Автори: Ковальов Микола Олександрович, Жуков Ігор Анатолійович, Кубіцкій Валерій Івановіч
Формула / Реферат
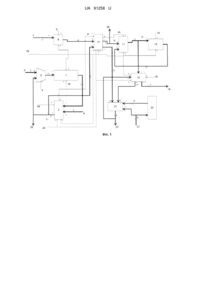
Цифровий інтегро-арифметичний пристрій, що містить регістр підінтегральної функції, перший блок додавання, комутатор, групу входів приросту підінтегральної функції, групу входів початкових умов, перший вхід синхронізації пристрою, групу входів приросту аргументу, регістр приросту аргументу, другий і третій входи синхронізації пристрою, другий блок додавання, регістр результату, регістр залишку інтегралу, четвертий вхід синхронізації пристрою, групу виходів пристрою, п'ятий вхід синхронізації пристрою, перший блок множення, шостий і сьомий входи синхронізації пристрою, при цьому група виходів регістра підінтегральної функції зв'язана з першою групою входів першого блока додавання, перша група виходів якого зв'язана з першою групою входів комутатора, група виходів якого зв'язана з першою групою входів регістра підінтегральної функції, група входів приросту підінтегральної функції зв'язана з другою групою входів першого блока додавання, група входів початкових умов зв'язана з другою групою входів комутатора, третій вхід якого зв'язаний з першим входом синхронізації пристрою, група входів приросту аргументу зв'язана з першою групою входів регістра приросту аргументу, друга група входів якого зв'язана з другим входом синхронізації пристрою, третій вхід синхронізації пристрою зв'язаний з другим входом регістра підінтегральної функції, група виходів другого блока додавання зв'язана з першими групами входів регістра результату і регістра залишку інтегралу, четвертий вхід синхронізації пристрою зв'язаний з другим входом регістра залишку інтегралу, перша група виходів пристрою зв'язана з групою виходів регістра результату, другий вхід якого зв'язаний з п'ятим входом синхронізації пристрою, перша група виходів першого блока додавання зв'язана з першою групою входів першого блока множення, перша група виходів якого зв'язана з першою групою входів другого блока додавання, другий вхід якого зв'язаний з другим виходом першого блока множення, друга група входів якого зв'язана з групою виходів регістра приросту аргументу, третій вхід якого зв'язаний з шостим входом синхронізації пристрою, який зв'язаний з третіми входами регістра підінтегральної функції, першого та другого блоків додавання, регістра результату, регістра залишку інтегралу, першого блока множення, другий вихід першого блока додавання зв'язаний з четвертим входом першого блока множення, сьомий вхід синхронізації пристрою зв'язаний з четвертим входом першого блока додавання, група виходів регістра залишку інтегралу зв'язана з четвертою групою входів другого блока додавання, який відрізняється тим, що до складу пристрою введені другий блок множення, блок матричного перетворення, суматори в складі перших блоків додавання та множення мають керовані ланцюги розповсюдження переносів, крім того в пристрій введені група входів коефіцієнтів утворюючого полінома, друга група виходів пристрою, восьмий вхід синхронізації пристрою, третя та четверта групи виходів пристрою група виходів пристрою, при цьому група виходів другого блока множення зв'язана з першою групою входів блока матричного перетворення, група входів коефіцієнтів утворюючого полінома зв'язана з групою входів другого блока множення та другою групою входів блока матричного перетворення, група виходів якого зв'язана з другою групою виходів пристрою і четвертою групою входів регістра результату, п'ятий вхід якого зв'язаний з восьмим входом синхронізації пристрою, який зв'язаний з п'ятими входами перших блоків додавання та множення відповідно, третя група виходів пристрою зв'язана з першою групою виходів першого блока додавання, третя група виходів першого блока множення зв'язана з третьою групою входів блока матричного перетворення, четверта група входів якого зв'язана з другою групою виходів регістра результату, четверта група виходів пристрою зв'язана з першою групою виходів першого блока множення.
Текст
Реферат: Цифровий інтегро-арифметичний пристрій містить регістр підінтегральної функції, перший блок додавання, комутатор, групу входів приросту підінтегральної функції, групу входів початкових умов, перший вхід синхронізації пристрою, групу входів приросту аргументу, регістр приросту аргументу, другий і третій входи синхронізації пристрою, другий блок додавання, регістр результату, регістр залишку інтегралу, четвертий вхід синхронізації пристрою, групу виходів пристрою, п'ятий вхід синхронізації пристрою, перший блок множення, шостий і сьомий входи синхронізації пристрою, другий блок множення, блок матричного перетворення, група входів коефіцієнтів утворюючого полінома, друга група виходів пристрою, восьмий вхід синхронізації пристрою, третя та четверта групи виходів пристрою. UA 91258 U (54) ЦИФРОВИЙ ІНТЕГРО-АРИФМЕТИЧНИЙ ПРИСТРІЙ UA 91258 U UA 91258 U 5 10 15 20 25 30 35 40 45 50 55 Корисна модель належить до засобів обчислювальної техніки та може застосовуватись в цифрових інтегруючих структурах, реалізованих на базі програмувальних логічних інтегральних схем для розподілених систем обробки даних, в яких використовується система передачі дискретної інформації з високою достовірністю. Перший відомий цифровий інтегратор [1] містить групу входів початкових умов, групу входів синхронізації, елементи І-АБО, групу входів приросту аргументу, регістр приросту аргументу, регістр підінтегральної функції, перший і другий блоки додавання, блок запам'ятовування таблиці множення, блоки затримки, блок запам'ятовування таблиці додавання, регістр залишку інтегралу, регістр результату, групу виходів приросту інтегралу, групу входів приросту підінтегральної функції та комутатор. В ньому реалізується тільки операція чисельного інтегрування, що не дозволяє безпосередньо застосовувати його в розподілених системах обробки даних з використанням системи передачі дискретної інформації з високою достовірністю. Другий відомий пристрій для множення елементів скінченних полів GF(2n ) [2] містить входи коефіцієнтів утворюючого полінома, входи першого співмножника, входи другого співмножника, блок формування часткових добутків, (n 1) блок матричного перетворення, блок додавання, блок множення та виходи результату. Недоліком другого відомого пристрою є обмежені функціональні можливості, зумовлені тим, що він виконує тільки операцію множення елементів скінченних полів GF(2n ) , що не дозволяє безпосередньо застосовувати його для реалізації інших математичних операцій в розподілених системах обробки даних. Найбільш близьким аналогом є цифровий інтегратор [3], який містить регістр підінтегральної функції, перший блок додавання, комутатор, групу входів приросту підінтегральної функції, групу входів початкових умов, перший вхід синхронізації пристрою, групу входів приросту аргументу, регістр приросту аргументу, другий і третій входи синхронізації пристрою, другий блок додавання, регістр результату, регістр залишку інтегралу, четвертий вхід синхронізації пристрою, групу виходів пристрою, п'ятий вхід синхронізації пристрою, блок множення, шостий і сьомий входи синхронізації пристрою. Пристрій дозволяє реалізувати тільки операцію чисельного інтегрування над даними з фіксованою точкою однакової розрядності, по модулю меншими за одиницю, у двійковій та четвертинній симетричних надлишкових системах числення з цифрами {-1, 0, 1} та {-2,-1, 0, 1, 2} відповідно. Це унеможливлює безпосереднє його застосовування в розподілених системах обробки даних з використанням системи передачі дискретної інформації з високою достовірністю. Тобто його недоліком є також обмежені функціональні можливості. В основу корисної моделі поставлено задачу удосконалення цифрового інтегратора за рахунок додаткової реалізації ним операцій додавання, віднімання та множення елементів скінченних полів GF(2n ) . Це дозволяє безпосередньо застосовувати його як для реалізації чисельного інтегрування, так і кодування та декодування циклічних поліноміальних кодів оброблюваних даних, які необхідно передавати з високою достовірністю в розподілених системах обробки даних. Таким чином розширюються функціональні можливості та сфера застосовності цифрового інтегратора. Поставлена задача вирішується завдяки цифровому інтегро-арифметичному пристрою, що містить регістр підінтегральної функції, перший блок додавання, комутатор, групу входів приросту підінтегральної функції, групу входів початкових умов, перший вхід синхронізації пристрою, групувходів приросту аргументу, регістр приросту аргументу, другий і третій входи синхронізації пристрою, другий блок додавання, регістр результату, регістр залишку інтегралу, четвертий вхід синхронізації пристрою, групу виходів пристрою, п'ятий вхід синхронізації пристрою, перший блок множення, шостий і сьомий входи синхронізації пристрою, при цьому група виходів регістра підінтегральної функції зв'язана з першою групою входів першого блока додавання, перша група виходів якого зв'язана з першою групою входів комутатора, група виходів якого зв'язана з першою групою входів регістра підінтегральної функції, група входів приросту підінтегральної функції зв'язана з другою групою входів першого блока додавання, група входів початкових умов зв'язана з другою групою входів комутатора, третій вхід якого зв'язаний з першим входом синхронізації пристрою, група входів приросту аргументу зв'язана з першою групою входів регістра приросту аргументу, друга група входів якого зв'язана з другим входом синхронізації пристрою, третій вхід синхронізації пристрою зв'язаний з другим входом регістра підінтегральної функції, група виходів другого блока додавання зв'язана з першими групами входів регістра результату і регістра залишку інтегралу, четвертий вхід синхронізації пристрою зв'язаний з другим входом регістра залишку інтегралу, перша група виходів пристрою 1 UA 91258 U 5 10 15 20 25 30 35 40 45 50 55 60 зв'язана з групою виходів регістра результату, другий вхід якого зв'язаний з п'ятим входом синхронізації пристрою, перша група виходів першого блока додавання зв'язана з першою групою входів першого блока множення, перша група виходів якого зв'язана з першою групою входів другого блока додавання, другий вхід якого зв'язаний з другим виходом першого блока множення, друга група входів якого зв'язана з групою виходів регістра приросту аргументу, третій вхід якого зв'язаний з шостим входом синхронізації пристрою, який зв'язаний з третіми входами регістра підінтегральної функції, першого та другого блоків додавання, регістра результату, регістра залишку інтегралу, першого блока множення, другий вихід першого блока додавання зв'язаний з четвертим входом першого блока множення, сьомий вхід синхронізації пристрою зв'язаний з четвертим входом першого блока додавання, група виходів регістра залишку інтегралу зв'язана з четвертою групою входів другого блока додавання. До складу пристрою введені другий блок множення, блок матричного перетворення, суматори в складі перших блоків додавання та множення мають керовані ланцюги розповсюдження переносів, крім того в пристрій введені група входів коефіцієнтів утворюючого полінома, друга група виходів пристрою, восьмий вхід синхронізації пристрою, третя та четверта групи виходів пристрою, при цьому група виходів другого блока множення зв'язана з першою групою входів блока матричного перетворення, група входів коефіцієнтів утворюючого полінома зв'язана з групою входів другого блока множення та другою групою входів блока матричного перетворення, група виходів якого зв'язана з другою групою виходів пристрою і четвертою групою входів регістра результату, п'ятий вхід якого зв'язаний з восьмим входом синхронізації пристрою, який зв'язаний з п'ятими входами перших блоків додавання та множення відповідно, третя група виходів пристрою зв'язана з першою групою виходів першого блока додавання, третя група виходів першого блока множення зв'язана з третьою групою входів блока матричного перетворення, четверта група входів якого зв'язана з другою групою виходів регістра результату, четверта група виходів пристрою зв'язана з першою групою виходів першого блока множення. Введення другого блока множення, блока матричного перетворення, керування ланцюгами розповсюдження переносів в суматорах перших блоків додавання та множення, а також введення нових зв'язків дозволяють додатково до реалізації чисельного інтегрування виконувати операції додавання, віднімання, множення та їх комбінації елементів скінченних полів GF(2n ) . Суть корисної моделі пояснюється кресленнями, де на фіг. 1 наведена структурна схема запропонованого пристрою, на фіг. 2 - часова діаграма роботи пристрою для розрядності даних n5. Цифровий інтегро-арифметичний пристрій містить регістр підінтегральної функції 1 (див. фіг. 1), перший блок додавання 2, комутатор 3, групу входів приросту підінтегральної функції 4, групу входів початкових умов 5, перший вхід синхронізації пристрою 6, групу входів приросту аргументу 7, регістр приросту аргументу 8, другий і третій входи синхронізації пристрою 9 і 10 відповідно, другий блок додавання 11, регістр результату 12, регістр залишку інтегралу 13, четвертий вхід синхронізації пристрою 14, групу виходів пристрою 15, п'ятий вхід синхронізації пристрою 16, перший блок множення 17, шостий і сьомий входи синхронізації пристрою 18 і 19 відповідно, другий блок множення 20, блок матричного перетворення 21, група входів коефіцієнтів утворюючого полінома 22, друга група виходів пристрою 23, восьмий вхід синхронізації пристрою 24, третя та четверта групи виходів пристрою 25 і 26 відповідно. Група виходів регістра підінтегральної функції 1 зв'язана з першою групою входів першого блока додавання 2, перша група виходів якого зв'язана з першою групою входів комутатора 3, група виходів якого зв'язана з першою групою входів регістра підінтегральної функції 1. Група входів приросту підінтегральної функції 4 зв'язана з другою групою входів першого блока додавання 2. Група входів початкових умов 5 зв'язана з другою групою входів комутатора 3, третій вхід якого зв'язаний з першим входом синхронізації пристрою 6, група входів приросту аргументу 7 зв'язана з першою групою входів регістра приросту аргументу 8, друга група входів якого зв'язана з другим входом синхронізації пристрою 9. Третій вхід синхронізації пристрою 10 зв'язаний з другим входом регістра підінтегральної функції 1. Група виходів другого блока додавання 11 зв'язана з першими групами входів регістра результату 12 і регістра залишку інтегралу 13. Четвертий вхід синхронізації пристрою 14 зв'язаний з другим входом регістра залишку інтегралу 13. Група виходів пристрою 15 зв'язана з групою виходів регістра результату 12, другий вхід якого зв'язаний з п'ятим входом синхронізації пристрою 16. Перша група виходів першого блока додавання 2 зв'язана з першою групою входів першого блока множення 17, перша група виходів якого зв'язана з першою групою входів другого блока додавання 11, другий вхід якого зв'язаний з другим виходом першого блока множення 17, друга група входів якого 2 UA 91258 U 5 10 15 20 25 30 зв'язана з групою виходів регістра приросту аргументу 8, третій вхід якого зв'язаний з шостим входом синхронізації пристрою 18, який зв'язаний з третіми входами регістра підінтегральної функції 1, першого та другого блоків додавання 2 і 11 відповідно, регістра результату 12, регістра залишку інтегралу 13, перший блока множення 17. Другий вихід першого блока додавання 2 зв'язаний з четвертим входом першого блока множення 17. Сьомий вхід синхронізації пристрою 19 зв'язаний з четвертим входом першого блока додавання 2. Група виходів регістра залишку інтегралу 13 зв'язана з четвертою групою входів другого блока додавання 11. Група входів другого блока множення 20 та друга група входів блока матричного перетворення 21 зв'язані з групою входів коефіцієнтів утворюючого полінома 22. Група виходів блока матричного перетворення 21 зв'язана з другою групою виходів пристрою 23 і четвертою групою входів регістра результату 12, п'ятий вхід якого зв'язаний з восьмим входом синхронізації пристрою 24, який зв'язаний з п'ятими входами перших блоків додавання 2 та множення 17 відповідно. Третя група виходів пристрою 25 зв'язана з першою групою виходів першого блока додавання 2. Третя група виходів першого блока множення 17 зв'язана з третьою групою входів блока матричного перетворення 21, четверта група входів якого зв'язана з другою групою виходів регістра результату 12, четверта група виходів пристрою 26 зв'язана з першою групою виходів першого блока множення 17. Пристрій може бути побудований наступним чином. Основу пристрою для реалізації чисельного інтегрування складають операційні блоки додавання 2 і 11, а також перший блок множення 17. Ці блоки є квазіпаралельними і відрізняються неавтономним режимом функціонування. В середині блоків інформація обробляється у паралельному вигляді, а між блоками передається послідовно. Алгоритми роботи і способи реалізації таких блоків відомі [4, 5]. Обчислення в них проводиться над даними з фіксованою точкою однакової розрядності, по модулю меншими за одиницю, у двійковій симетричній надлишковій системі числення з цифрами {-1, 0, 1}. Тому більшість груп входів і виходів у пристрою складаються з 2-х сигнальних ліній, а цифри кодуються наступним чином: -1="01", 0="00", 1="10". В першому режимі роботи пристрій виконує чисельне інтегрування за Стілтьєсом і функціонує за таким алгоритмом: z y е(i 1) ( yp ypi ) 2n Si q (i 1) (i 1) 0 , z(i 1) Pn (z(i 1) ) n 1 S(i 1) P 2n (z(i 1) ) де z(i 1) - неквантоване значення приросту інтегралу на (i 1) -у кроці; z(i 1) - квантоване значення приросту інтегралу на (i 1) -у кроці; y е(i1) - екстрапольоване значення аргументу q інтегрування для (i 1) -о кроку; y p - значення підінтегральної функції на (i 1) -у кроці; y pi (i 1) приріст підінтегральної функції на i-у кроці; S i , S(i1) - значення залишків інтегралу на i-у та 35 (i 1) -у кроках відповідно; Plm - операція виділення розрядів з m по l (від'ємні значення вказують на розряд справа від точки). В першому блоці множення 17 виконують арифметичну операцію виду: Z 22 XY , У кожному з блоків додавання 2 і 11 виконують арифметичну операцію виду: 40 45 Z 2 2 ( X Y ) . В обох випадках забезпечується суміщення порозрядного введення операндів X та Y зі старших розрядів і порозрядного формування результату Z , старший розряд якого отримують із запізненням на два такти. Регістр підінтегральної функції 1, регістр приросту аргументу 8, регістр результату 12 і регістр залишку інтегралу 13 фактично є регістрами зсуву, а комутатор 3 є мультиплексором. В другому режимі роботи пристрій виконує наступні операції над елементами скінченних полів GF(2n ) : a( x) b( x) ; {(a( x ) b( x )) d( x )}(mod d 2, gm ( x )) . 3 UA 91258 U 5 Тут a( x ) , b( x ) , c( x ) , d( x ) - многочлени n-о степеня, gm ( x ) - утворюючий поліном m -о степеня (2 m n) . Операцію додавання (віднімання) виконують як суму по модулю 2 відповідних коефіцієнтів многочленів, а операцію множення - як звичайне множення многочленів з отриманням коефіцієнтів многочлена добутку і залишку від добутку по подвійному модулю 2 утворюючого полінома gm ( x ) . Перші блоки додавання 2 і множення 17 реалізують операції додавання (віднімання) і множення відповідно над елементами скінченних полів 10 15 GF(2n ) , для чого забороняють розповсюдження сигналів переносів в суматорах цих блоків, що формують значення змінної Hi [4, 5], крім старших 2-х її розрядів. При цьому операнди (доданки або співмножники) подаються на вхід означених блоків послідовно зі старших розрядів. Таким же чином с затримкою в 2 такти формуються й результати. Цифри результатів та операндів також представлені у двійковій симетричній надлишковій системі числення з цифрами {-1, 0, 1} і кодуються як: -1="01", 0="00", 1="10". Це дозволяє одразу використовувати результати як операнди для інших подібних квазіпаралельних пристроїв, що виконують інші операції над елементами скінченних полів GF(2n ) . При необхідності можна легко перевести результат у двійкову систему числення з цифрами {0, 1}, безпосередньо отримавши коефіцієнти результуючого полінома. Для отримання 20 25 30 35 40 45 50 залишку від добутку по подвійному модулю 2 утворюючого полінома gm ( x ) в пристрій введені другий блок множення 20 та блок матричного перетворення 21, структура та функціонування яких описані в [2]. Перший з них призначений для визначення коефіцієнта розширення поля m , другий - обчислення поточної суми часткових добутків і приведення її по подвійному модулю 2 утворюючого полінома gm ( x ) . Пристрій працює наступним чином. Його роботу тактують по шостому входу синхронізації 18. При відсутності сигналу на восьмому вході синхронізації 24 пристрій в першому режимі роботи, виконуючи чисельне інтегрування за Стілтьєсом. Для реалізації пристроєм операцій над елементами скінченних полів GF(2n ) в другому режимі роботи впродовж всього періоду їх виконання подають сигнал на восьмий вхід синхронізації 24. За цим сигналом блокуються ланцюги розповсюдження переносів в перших блоках додавання 2 та множення 17, а в регістрі результату 12 не відбуваються зсуви. Крім того, на групу входів коефіцієнтів утворюючого полінома 22 подають значення його коефіцієнтів, що призводить до формування сигналу в групі виходів блоку множення 20, відповідного коефіцієнту розширення поля m . Перед початком роботи за сигналами на першому і третьому входах синхронізацій пристрою 6 і 10 відповідно початкове значення підінтегральної функції yp0 або коефіцієнти многочлену a( x ) (в залежності від режиму роботи пристрою) через другу групу входів комутатора 3 послідовно завантажують за п тактів через першу групу входів в регістр підінтегральної функції 1. Після цього розпочинають роботу цифрового інтегро-арифметичного пристрою. Крок обчислення квантованого значення інтегрального приросту або z(i 1) {(a( x ) b( x )) d( x )}(mod d 2, gm ( x )) (в залежності від режиму роботи пристрою) починають з подачі впродовж одного такту стартового сигналу на сьомий вхід синхронізації пристрою 19. Відповідно з ним здійснюють початкову установку регістрів першого блока додавання 2. Після цього по сигналу на третьому вході синхронізації пристрою 10 впродовж n тактів на першу групу входів першого блока додавання 2 порозрядно подають значення підінтегральної функції на (i 1) -у кроці y p(i 1) або коефіцієнти многочлену a( x ) (в залежності від режиму роботи пристрою), починаючи зі старших розрядів. Водночас на другу групу входів цього блока таким же чином подають через групу входів пристрою 4 приріст підінтегральної функції на i-у кроці y pi або коефіцієнти многочлену b( x ) (в залежності від режиму роботи пристрою). І на його першій групі виходів із затримкою на 2 такти отримують, починаючи із старших розрядів, в залежності від режиму роботи пристрою суму, яка має вигляд: t1 ypi yp(i 1) ypi , або в іншому режимі роботи пристрою t1 a( x) b( x) . 4 UA 91258 U 5 В обох режимах роботи пристрою отримані значення (розряди значення підінтегральної функції на i-у кроці y pi або цифри коефіцієнтів отриманого в результаті операції додавання (віднімання) многочлена) подають на третю групу виходів пристрою 25. При цьому водночас з цим завантажують отримувані розряди значення підінтегральної функції y pi в регістр підінтегральної функції 1 через першу групу входів комутатора 3 та першу групу входів регістра підінтегральної функції 1 відповідно до згаданого вище сигналу на третьому вході синхронізації пристрою 10, а також подають його на першу групу входів першого блока додавання 2. Перед отримуванням старшого розряду значення t1 на другому виході 10 15 20 25 30 35 першого блока додавання 2 формується сигнал s t тривалістю в один такт. Він надходить на четвертий вхід першого блока множення 17, і за цим стартовим сигналом відбувається початкове встановлення регістрів цього блока. Одночасно з цим за сигналом на другому вході синхронізації пристрою 9 тривалістю п тактів з другої групи виходів регістра приросту аргументу 8 на другу групу входів першого блока множення 17 порозрядно надходить екстрапольоване значення аргументу інтегрування для (i 1) -о кроку yе(i1) або коефіцієнти многочлену d( x ) (в q залежності від режиму роботи пристрою), починаючи із старших розрядів. Із затримкою на 2 такти на першій групі виходів першого блока множення 17 отримують, починаючи із старших розрядів, в залежності від режиму роботи пристрою добуток розрядністю (2n) : t 2 z(i1) t1yе(i1) ypiyе(i1) , q q тобто черговий неквантований приріст інтегралу, або многочлен t 2 t1 d( x) (a( x) b( x)) d( x) . В цьому режимі роботи отримувані цифри добутку подають на четверту групу виходів пристрою 26. Залишок від цього добутку по подвійному модулю 2 утворюючого полінома gm ( x ) отримують наступним чином. На кожному такті порозрядного вводу коефіцієнтів вхідних многочленів t1 та d( x ) на третій групі виходів першого блока додавання 17 формують черговий частковий добуток виду ( xi Yi yi Xi1) [4, 5]. Його подають на третю групу входів блока матричного перетворення 21. В ньому, використовуючи значення коефіцієнта розширення поля m на першій групі входів, коефіцієнтів утворюючого полінома gm ( x ) на другій групі входів, поточну суму часткових добутків (зберігають в регістрі результату 12) на четвертій групі входів, формують нове значення суми часткових добутків з приведенням її по подвійному модулю 2 утворюючого полінома gm ( x ) . Це значення з групи виходів блока матричного перетворення 21 подають на четверту групу входів регістра результату 12 і фіксують там до наступного такту. Таким чином, після вводу молодших розрядів значень коефіцієнтів многочленів t1 та d( x ) на групі виходів блока матричного перетворення 21 сформують значення залишку, яке подають на другу групу виходів пристрою 23. В іншому режимі роботи пристрою перед формуванням старшого розряду неквантованого приросту інтегралу z(i 1) на другому виході першого блока множення 17 формується сигнал st2 тривалістю в один такт. Він надходить на другий вхід другого блока додавання 11, і за цим стартовим сигналом здійснюється початкове встановлення регістрів зазначеного блока. Отримувані розряди неквантованого приросту інтегралу z(i 1) послідовно надходять на першу 40 групу входів другого блока додавання 11. Водночас на його четверту групу входів протягом n тактів з другої групи виходів регістра залишку інтегралу 13 подається нульове значення, а протягом наступних n тактів згідно з сигналом на четвертому вході синхронізації пристрою 14 значення залишку інтегралу S i , на i-у кроці. Тоді із затримкою на 2 такти на групі виходів 45 другого блока додавання 11 отримують, починаючи із старших розрядів, суму розрядністю (2n) , що має вигляд: 50 t 3 t 3 2 n S i . Старші n розрядів значення t 3 становлять квантоване значення приросту інтегралу z(i 1) . Саме вони згідно з сигналом на п'ятому вході синхронізації пристрою 16 тривалістю n тактів завантажуються у регістр результату 12 через його першу групу входів. Молодші n розрядів значення t 3 становлять нове значення залишку інтегралу S(i1) . Вони за згаданим вище 5 UA 91258 U 5 10 15 20 25 30 35 40 45 50 55 60 сигналом на четвертому вході синхронізації пристрою 14 протягом n тактів завантажуються в регістр залишку інтегралу 13 через його першу групу входів. На відміну від аналога запропонована корисна модель цифрового інтегро-арифметичного пристрою, крім виконання чисельного інтегрування, завдяки незначному ускладненню апаратури додатково дозволяє виконувати операції додавання, віднімання, множення елементів скінченних полів GF(2n ) та їх комбінації. Пристрій безпосередньо можна застосовувати для реалізації як чисельного інтегрування, так і кодування та декодування циклічних поліноміальних кодів, які представляють інтегральні змінні та їх прирости. Таке розширення функціональних можливостей дозволяє без значних додаткових апаратних витрат скоротити часові витрати на обробку та передавання інформації з високою достовірністю, підвищити надійність цифрових інтегруючих структур, ефективно використовувати їх в розподілених системах обробки даних з високими вимогами до параметрів надійності й швидкодії. Таким чином розширюються функціональні можливості та сфера застосовності цифрового інтегратора, що стало можливим завдяки введенню нових блоків і конструктивних зв'язків, а також зміні побудови існуючих блоків і зв'язків. Джерела інформації: 1. Авторське свідоцтво СРСР № 1330629, кл. G06F 7/64, 1985. 2. Патент України на корисну модель № 43629, МПК (2009) кл. Н03М 7/00, 2009. 3. Патент України на винахід № 87073, МПК (2009) G01S 13/00, G01S 17/00, G06F 7/60, 2009 (прототип). 4. Жабин В.И., Корнейчук В.И., Тарасенко В.П. Метод быстрого неавтономного воспроизведения функций // Управляющие системы и машины. - 1977. - № 3. - С. 96-101. 5. Жабин В.И., Корнейчук В.И., Тарасенко В.П. Методы вычисления некоторых функций при поразрядном вводе и выводе информации // Известия вузов. Приборостроение. - 1978. - № 2. С. 64-69. ФОРМУЛА КОРИСНОЇ МОДЕЛІ Цифровий інтегро-арифметичний пристрій, що містить регістр підінтегральної функції, перший блок додавання, комутатор, групу входів приросту підінтегральної функції, групу входів початкових умов, перший вхід синхронізації пристрою, групу входів приросту аргументу, регістр приросту аргументу, другий і третій входи синхронізації пристрою, другий блок додавання, регістр результату, регістр залишку інтегралу, четвертий вхід синхронізації пристрою, групу виходів пристрою, п'ятий вхід синхронізації пристрою, перший блок множення, шостий і сьомий входи синхронізації пристрою, при цьому група виходів регістра підінтегральної функції зв'язана з першою групою входів першого блока додавання, перша група виходів якого зв'язана з першою групою входів комутатора, група виходів якого зв'язана з першою групою входів регістра підінтегральної функції, група входів приросту підінтегральної функції зв'язана з другою групою входів першого блока додавання, група входів початкових умов зв'язана з другою групою входів комутатора, третій вхід якого зв'язаний з першим входом синхронізації пристрою, група входів приросту аргументу зв'язана з першою групою входів регістра приросту аргументу, друга група входів якого зв'язана з другим входом синхронізації пристрою, третій вхід синхронізації пристрою зв'язаний з другим входом регістра підінтегральної функції, група виходів другого блока додавання зв'язана з першими групами входів регістра результату і регістра залишку інтегралу, четвертий вхід синхронізації пристрою зв'язаний з другим входом регістра залишку інтегралу, перша група виходів пристрою зв'язана з групою виходів регістра результату, другий вхід якого зв'язаний з п'ятим входом синхронізації пристрою, перша група виходів першого блока додавання зв'язана з першою групою входів першого блока множення, перша група виходів якого зв'язана з першою групою входів другого блока додавання, другий вхід якого зв'язаний з другим виходом першого блока множення, друга група входів якого зв'язана з групою виходів регістра приросту аргументу, третій вхід якого зв'язаний з шостим входом синхронізації пристрою, який зв'язаний з третіми входами регістра підінтегральної функції, першого та другого блоків додавання, регістра результату, регістра залишку інтегралу, першого блока множення, другий вихід першого блока додавання зв'язаний з четвертим входом першого блока множення, сьомий вхід синхронізації пристрою зв'язаний з четвертим входом першого блока додавання, група виходів регістра залишку інтегралу зв'язана з четвертою групою входів другого блока додавання, який відрізняється тим, що до складу пристрою 6 UA 91258 U 5 10 15 введені другий блок множення, блок матричного перетворення, суматори в складі перших блоків додавання та множення мають керовані ланцюги розповсюдження переносів, крім того в пристрій введені група входів коефіцієнтів утворюючого полінома, друга група виходів пристрою, восьмий вхід синхронізації пристрою, третя та четверта групи виходів пристрою група виходів пристрою, при цьому група виходів другого блока множення зв'язана з першою групою входів блока матричного перетворення, група входів коефіцієнтів утворюючого полінома зв'язана з групою входів другого блока множення та другою групою входів блока матричного перетворення, група виходів якого зв'язана з другою групою виходів пристрою і четвертою групою входів регістра результату, п'ятий вхід якого зв'язаний з восьмим входом синхронізації пристрою, який зв'язаний з п'ятими входами перших блоків додавання та множення відповідно, третя група виходів пристрою зв'язана з першою групою виходів першого блока додавання, третя група виходів першого блока множення зв'язана з третьою групою входів блока матричного перетворення, четверта група входів якого зв'язана з другою групою виходів регістра результату, четверта група виходів пристрою зв'язана з першою групою виходів першого блока множення. 7 UA 91258 U Комп’ютерна верстка Л. Литвиненко Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 8
ДивитисяДодаткова інформація
Автори англійськоюZhukov Ihor Anatoliiovych, Kovaliov Mykola Oleksandrovych, Kubytskyi Valerii Ivanovych
Автори російськоюЖуков Игорь Анатольевич, Ковалев Николай Александрович, Кубицкий Валерий Иванович
МПК / Мітки
МПК: G06F 7/60, G06F 7/57, G06F 7/64
Мітки: інтегро-арифметичний, цифровий, пристрій
Код посилання
<a href="https://ua.patents.su/10-91258-cifrovijj-integro-arifmetichnijj-pristrijj.html" target="_blank" rel="follow" title="База патентів України">Цифровий інтегро-арифметичний пристрій</a>
Попередній патент: Спосіб попередження інфаркту міокарда при експериментальній гострій ішемії-реперфузії міокарда
Наступний патент: Спосіб лікування часткового нейрорахішизису
Випадковий патент: Сигареторобна машина і спосіб виготовлення сигарет