Спосіб визначення показників деформаційного зміцнення конструкційного титанового сплаву
Номер патенту: 104665
Опубліковано: 25.02.2014
Автори: Шиян Артур Віталійович, Мєшков Юрій Якович, Івасишин Орест Михайлович, Котречко Сергій Олексійович, Марковський Павло Євгенович
Формула / Реферат
Спосіб визначення показників деформаційного зміцнення конструкційного титанового сплаву, при якому проводять випробування стандартних гладких циліндричних зразків на одновісне розтягнення в інтервалі температур від 4К до 293К, визначають при цьому базові механічні характеристики та характеристики дійсного напруження руйнування зразка SK і відносного рівномірного звуження ![]() , будують експериментальну залежність опору пластичній деформації
, будують експериментальну залежність опору пластичній деформації ![]() в області рівномірної деформації, який відрізняється тим, що розраховують величину інтенсивності напружень руйнування зразка
в області рівномірної деформації, який відрізняється тим, що розраховують величину інтенсивності напружень руйнування зразка ![]() , будують експериментальні залежності опору пластичній деформації
, будують експериментальні залежності опору пластичній деформації ![]() в області нерівномірної деформації, що характеризуються зберіганням властивості лінійності або наявністю зламу і підвищенням кута нахилу цієї залежності в інтервалі змін міцності від дійсного напруження на границі міцності SB до величини інтенсивності напружень руйнування зразка
в області нерівномірної деформації, що характеризуються зберіганням властивості лінійності або наявністю зламу і підвищенням кута нахилу цієї залежності в інтервалі змін міцності від дійсного напруження на границі міцності SB до величини інтенсивності напружень руйнування зразка ![]() , встановлюють групу сплаву в залежності від співвідношення величин показників деформаційного зміцнення при деформаціях менших та більших за рівномірну, додатково будують експериментальні залежності
, встановлюють групу сплаву в залежності від співвідношення величин показників деформаційного зміцнення при деформаціях менших та більших за рівномірну, додатково будують експериментальні залежності ![]() , розраховують на їх основі емпіричні коефіцієнти та визначають показники деформаційного зміцнення за формулами: для I-ої групи сплавів:
, розраховують на їх основі емпіричні коефіцієнти та визначають показники деформаційного зміцнення за формулами: для I-ої групи сплавів:
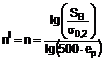 ,
,
для II-ої групи сплавів:
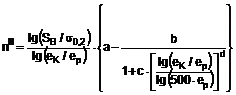 ,
,
де: ![]() - умовна границя текучості, МПа,
- умовна границя текучості, МПа,
![]() - дійсне напруження на границі міцності, МПа,
- дійсне напруження на границі міцності, МПа,
![]() - границя міцності, МПа,
- границя міцності, МПа,
![]() - дійсна рівномірна деформація,
- дійсна рівномірна деформація,
![]() - відносне рівномірне звуження, в частках,
- відносне рівномірне звуження, в частках,
![]() - дійсна деформація після руйнування зразка,
- дійсна деформація після руйнування зразка,
![]() - відносне звуження після руйнування зразка, в частках,
- відносне звуження після руйнування зразка, в частках,
а = 82,23, b = 82,156, с = 0,041, d = 1,692 - емпіричні коефіцієнти.
Текст
Реферат: Винахід належить до галузі кольорової металургії, а саме - до способу визначення показників деформаційного зміцнення конструкційного титанового сплаву. Спосіб включає операції розтягування стандартного гладкого циліндричного зразка повздовж однієї вісі при різних температурах в інтервалі від 4К до 293К, визначення при цьому базових механічних характеристик та характеристик дійсного напруження руйнування зразка S K і відносного UA 104665 C2 (12) UA 104665 C2 рівномірного звуження p , побудови експериментальної залежності опору пластичній деформації lg f lge в області рівномірної деформації, розрахунку величини інтенсивності напружень руйнування зразка K , побудови експериментальних залежностей опору пластичній i деформації lg f lge в області нерівномірної деформації, що характеризуються зберіганням властивості лінійності або наявністю зламу і підвищенням кута нахилу цієї залежності в інтервалі змін міцності від дійсного напруження на границі міцності S B до величини інтенсивності напружень руйнування зразка K , встановлення групи сплаву в залежності від i співвідношення величин показників деформаційного зміцнення при деформаціях менших та більших за рівномірну, додаткової побудови експериментальних залежностей , lg eK / ep lg K / SB i f lg SB / 0,2 lg 500 ep розрахунку на їх основі емпіричних коефіцієнтів та визначення показників деформаційного зміцнення за формулами: для I-ої групи сплавів: S lg B 0,2 , nI n lg 500 ep для II-ої групи сплавів: lg SB / 0,2 b nII a , d lg eK / ep lg eK / ep 1 c lg 500 ep де: 0,2 - умовна границя текучості, МПа, 1 - дійсне напруження на границі міцності, МПа, SB B 1 p B - границя міцності, МПа, 1 - дійсна рівномірна деформація, ep ln 1 p p - відносне рівномірне звуження, в частках, eK ln1 K - дійсна деформація після руйнування зразка, K - відносне звуження після руйнування зразка, в частках, а = 82,23, b = 82,156, с = 0,041, d = 1,692 - емпіричні коефіцієнти. Винахід забезпечує підвищення точності та інформативності визначення показників деформаційного зміцнення конструкційного титанового сплаву в області нерівномірної деформації за даними лише базових механічних характеристик 0,2 , B , K та характеристики відносного рівномірного звуження p за якими комплексно оцінюють спроможність опору переходу титанових сплавів в крихкий стан. UA 104665 C2 5 Винахід належить до галузі кольорової металургії, а саме – до дослідження властивостей твердих матеріалів шляхом прикладання статичних навантажень в інтервалі температур випробувань гладких зразків від 4К до 293К, і визначення показників деформаційного зміцнення конструкційного титанового сплаву. Відомий спосіб визначення показників деформаційного зміцнення металевих сплавів при випробуванні гладких циліндричних зразків на одновісний розтяг за формулою [1]: S lg B 0,2 n ep lg 0,002 , 1 SB B 1 p де: 1 ep ln 1 p 10 15 20 25 30 35 - дійсне напруження на границі міцності, МПа; - дійсна рівномірна деформація; B - границя міцності, МПа; p - відносне рівномірне звуження зразка, в частках. Недоліками даного способу є наступні: а) показники деформаційного зміцнення, визначені за даним способом в області рівномірної деформації, зберігають свою величину в області нерівномірної деформації лише для вузького кола металевих сплавів; б) не враховуються особливості поведінки залежності опору пластичній деформації в інтервалі змін міцності від дійсного напруження на границі міцності SB до величини дійсного напруження руйнування зразка SK. Найбільш близьким за технічною суттю та результатом, що досягається, до способу, що заявляється, є спосіб визначення показників деформаційного зміцнення конструкційного титанового сплаву, при якому враховують факт зламу залежності опору пластичній деформації в логарифмічних координатах в інтервалі змін міцності від дійсного напруження на границі міцності SB до величини дійсного напруження руйнування зразка SK. Таким чином, для розрахунку показників деформаційного зміцнення за основу приймають певну розрахункову лінійну залежність, що усереднює вплив ефекту зламу залежності опору пластичній деформації в області нерівномірної деформації, а величина самих показників представляє собою певну усереднену комбінацію їх значень як в області рівномірної, так і в області нерівномірної деформації. При цьому проводять випробування стандартних гладких циліндричних зразків на одновісне розтягнення при температурах від 4К до 293К, визначення базових механічних характеристик конструкційного титанового сплаву, будують експериментальну залежність опору пластичній деформації lg f lge в області рівномірної деформації та експериментальні залежності опору пластичній деформації lg f lge , що характеризуються зберіганням властивості лінійності або наявністю зламу і підвищенням кута нахилу цієї залежності в інтервалі змін міцності від дійсного напруження на границі міцності S B до величини дійсного напруження руйнування зразка SK, після чого визначають показник деформаційного зміцнення n за розрахунковою лінійною залежністю, що усереднює вплив ефекту зламу залежності опору пластичній деформації в області нерівномірної деформації, використовуючи наступну формулу [2]: S lg B 0,2 n lg 500 ep , 1 SB B 1 p де: 40 1 ep ln 1 p - дійсне напруження на границі міцності, МПа; - дійсна рівномірна деформація; B - границя міцності, МПа; p - відносне рівномірне звуження зразка, в частках. 1 UA 104665 C2 5 10 Разом з тим, спосіб визначення показника деформаційного зміцнення конструкційного титанового сплаву за прототипом має наступні недоліки: а) недостатню точність та інформативність щодо визначення показників деформаційного зміцнення для широкого кола конструкційних титанових сплавів по причині неврахування явища локалізації деформації в "шийці" зразка при визначенні дійсного напруження руйнування S K; б) відсутність методики розподілу конструкційних титанових сплавів за групами в залежності від співвідношення величин показників деформаційного зміцнення при деформаціях менших та більших за рівномірну; в) відсутність залежностей для визначення показників деформаційного зміцнення конструкційних титанових сплавів з різною природою поведінки залежності опору пластичній деформації в області нерівномірної деформації. В основу винаходу покладено задачу вдосконалення способу визначення показників деформаційного зміцнення конструкційного титанового сплаву з урахуванням особливостей поведінки залежності опору пластичній деформації lg f lge в області нерівномірної деформації. При цьому використовують базові механічні характеристики та характеристики 15 дійсного напруження руйнування зразка SK і відносного рівномірного звуження p , отримані в широкому інтервалі температур випробувань гладких зразків від 4К до 293К. Поставлену задачу вирішують шляхом врахування явища локалізації деформації в "шийці" зразка при розтягненні та отримання авторами достатньої кількості експериментальних даних для розрахунку K величини інтенсивності напружень руйнування зразка i . Далі будують експериментальну 20 залежність опору пластичній деформації lg f lge в області рівномірної деформації та експериментальні залежності опору пластичній деформації lg f lge , що характеризуються зберіганням властивості лінійності або наявністю зламу і підвищенням кута нахилу цієї залежності в інтервалі змін міцності від дійсного напруження на границі міцності S B до величини K 25 інтенсивності напружень руйнування зразка i . Після цього встановлюють групу сплаву в залежності від співвідношення величин показників деформаційного зміцнення при деформаціях менших та більших за рівномірну, додатково будують експериментальні залежності , lg eK / ep lg K / SB i f lg SB / 0,2 lg 500 ep розраховують на їх основі емпіричні коефіцієнти для кожної групи сплавів та встановлюють зв'язок між показниками деформаційного зміцнення в області нерівномірної деформації і базовими механічними характеристиками конструкційного 30 титанового сплаву, такими, як відносне звуження після руйнування зразка K , умовна границя текучості 0,2 , границя міцності B та допоміжною характеристикою відносного рівномірного 35 звуження p . Це дозволило авторам розробити загальну методику розподілу широкого кола конструкційних титанових сплавів за групами та визначення показників деформаційного зміцнення для сплавів кожної групи. Винахід дає можливість більш інформативно і точно визначати показники деформаційного зміцнення конструкційного титанового сплаву в області нерівномірної деформації за величинами основних механічних характеристик 0,2 , B , K та 40 45 характеристики відносного рівномірного звуження p , що, в свою чергу, дозволяє здійснювати комплексну оцінку їх властивостей та більш точно оцінювати спроможність опиратись переходу в крихкий стан. Поставлена задача вирішується тим, що у відомому способі визначення показників деформаційного зміцнення конструкційного титанового сплаву, при якому проводять випробування стандартних гладких циліндричних зразків на одновісний розтяг в інтервалі температур від 4К до 293К, визначення при цьому базових механічних характеристик та характеристик дійсного напруження руйнування зразка SK і відносного рівномірного звуження p , будують експериментальну залежність опору пластичній деформації lg f lge в області рівномірної деформації, згідно з винаходом, розраховують величину інтенсивності напружень K руйнування зразка i , будують експериментальні залежності опору пластичній деформації 50 lg f lge в області нерівномірної деформації, що характеризуються зберіганням властивості лінійності або наявністю зламу і підвищенням кута нахилу цієї залежності в інтервалі змін міцності від дійсного напруження на границі міцності SB до величини інтенсивності напружень 2 UA 104665 C2 K руйнування зразка i , встановлюють групу сплаву в залежності від співвідношення величин показників деформаційного зміцнення при деформаціях менших та більших за рівномірну, , розраховують на їх lg eK / ep lg K / SB i f lg SB / 0,2 lg 500 ep 5 додатково будують експериментальні залежності основі емпіричні коефіцієнти та визначають показники деформаційного зміцнення за формулами: для I-ої групи сплавів: S lg B 0,2 nI n lg 500 ep ; для II-ої групи сплавів: lg SB / 0,2 b nII a d lg eK / ep lg eK / ep 1 c lg 500 ep ; де: 0,2 - умовна границя текучості, МПа; 10 1 SB B 1 p - дійсне напруження на границі міцності, МПа; B - границя міцності, МПа; 1 ep ln 1 p - дійсна рівномірна деформація; p - відносне рівномірне звуження, в частках; 15 eK ln1 K - дійсна деформація після руйнування зразка; K - відносне звуження після руйнування зразка, в частках; а = 82,23; b=82,156; с = 0,041; d=1,692 - емпіричні коефіцієнти. За рахунок отримання авторами достатньої кількості експериментальних даних для розрахунку величини інтенсивності напружень руйнування зразка i , побудови залежностей lg f lge в області нерівномірної деформації, що характеризуються зберіганням властивості лінійності або наявністю зламу і підвищенням кута нахилу цієї залежності в інтервалі змін міцності від дійсного напруження на K 20 K границі міцності SB до величини інтенсивності напружень руйнування зразка i , додаткової , lg eK / ep lg K / SB i f lg SB / 0,2 lg 500 ep 25 побудови експериментальних залежностей запропонований спосіб дозволяє більш інформативно і точно визначати показники деформаційного зміцнення для широкого кола конструкційних титанових сплавів в області нерівномірної деформації за величинами основних механічних характеристик 0,2 , B , K та характеристики відносного рівномірного звуження p . При цьому автори використовують достатньо велику базу експериментальних даних механічних характеристик конструкційних титанових сплавів з 30 різними рівнями пластичності K та міцності 0,2 , отриманих за результатами випробувань в широкому інтервалі температур від 4К до 293К, а саме: значень відносного звуження після руйнування зразка K ; умовної границі текучості 0,2 ; границі міцності B ; дійсного напруження 35 руйнування зразка SK та відносного рівномірного звуження зразка p . Крім того, запропонований спосіб дозволив розробити загальну методику розподілу широкого кола конструкційних титанових сплавів за групами в залежності від співвідношення величин показників деформаційного зміцнення при деформаціях менших та більших за рівномірну, а також спосіб визначення показників деформаційного зміцнення для сплавів кожної групи з 3 UA 104665 C2 5 точністю, достатньою не тільки для інженерних розрахунків, але й наукових досліджень. Це дасть можливість здійснювати комплексний аналіз властивостей конструкційних титанових сплавів, у тому числі більш точно визначати характеристики крихкої міцності і механічної стабільності, тобто оцінювати спроможність цих сплавів чинити опір переходу у крихкий стан. Запропонований спосіб пояснюється таблицями та графіками, а саме: в таблиці 1 наведені значення базових механічних характеристик 0,2 , B , K деяких конструкційних титанових сплавів, а також результати розрахунку показників деформаційного I 10 зміцнення n n та nII в інтервалі температур випробувань від 4К до 293К; в таблиці 2 наведені значення вибіркового стандарту S, величини довірчого інтервалу та вірогідності Р для оцінки точності залежностей, які використовують для розрахунку показників деформаційного зміцнення конструкційного титанового сплаву; на фіг. 1 зображена схема залежностей опору пластичній деформації в логарифмічних I II координатах lg f lge для сплавів: I-ої групи tg n n (крива 1); II-ої групи tg n (крива 2); lg eK / ep lg K / SB i f lg SB / 0,2 lg 500 ep для досліджених на фіг. 2 зображені експериментальні залежності 15 конструкційних титанових сплавів, що належать до різних груп, у масштабі по координаті X: від 0 до 2,5; експериментальні дані, отримані в інтервалі температур випробувань від 4К до 293К: ▲ сплави I-ої групи (крива 1), ○ - сплави II-ої групи (крива 2); lg eK / ep lg K / SB i f lg SB / 0,2 lg 500 ep 20 на фіг. 3 зображені експериментальні залежності для досліджених конструкційних титанових сплавів, що належать до різних груп, у масштабі по координаті X: від 0 до 0,7; експериментальні дані, отримані в інтервалі температур випробувань від 4К до 293К: ▲ сплави I-ої групи (крива 1), ○ - сплави II-ої групи (крива 2); Спосіб реалізується наступним чином. K З метою розрахунку величини інтенсивності напружень руйнування зразка i , побудови 25 експериментальних залежностей lg f lge в області нерівномірної деформації, що характеризуються зберіганням властивості лінійності або наявністю зламу і підвищенням кута нахилу цієї залежності, додаткової побудови експериментальних залежностей , lg eK / ep lg K / SB i f lg SB / 0,2 lg 500 ep широкого охоплення матеріали для досліджень добирали за принципом максимально різноманітних комбінацій властивостей міцності та пластичності конструкційних титанових сплавів, при цьому діапазон характеристик міцності складав: від 0,2 30 35 40 = 570 МПа до 0,2 = 1925 МПа, а діапазон характеристик пластичності складав 1,0 % ≤ K ≤ 81,0 %. Крім цього, за об'єкти досліджень обирали конструкційні титанові сплави, що відносяться до різних класів за структурою, якістю, складом та призначенням, у тому числі особливого призначення, які використовують у криогенній техніці та для створення відповідальних конструкцій. Змінювали також різні режими термічної обробки і температуру випробувань в інтервалі від 4К до 293К. Всього в цих дослідженнях використовували результати більш ніж 300 вимірів деформаційних характеристик та характеристик міцності, отриманих при випробуванні стандартних гладких циліндричних зразків на одновісне статичне розтягнення більш ніж 200 видів конструкційних титанових сплавів. Проводять розтягування вздовж однієї вісі стандартних гладких циліндричних зразків та визначають базові механічні характеристики сплаву такі, як: K - відносне звуження після руйнування зразка; 0,2 - умовна границя текучості; B - границя міцності, а також характеристики дійсного напруження руйнування зразка SK та відносного рівномірного звуження p при температурах випробувань в інтервалі 4К ≤ Т вип ≤ 293К. 45 Загальна методика визначення показників деформаційного зміцнення конструкційного титанового сплаву полягає у наступному: 1) з метою урахування явища локалізації деформації в "шийці" при розтягненні зразка в інтервалі змін міцності від дійсного напруження на границі міцності S B до величини дійсного напруження руйнування зразка SK, що обумовлює необхідність розглядати "шийку" як 4 UA 104665 C2 концентратор напружень, розраховують величину інтенсивності напружень руйнування зразка K за відомими формулами [3]: i SK K i 1 2 / ln 1 / 2 , МПа, (1) де параметр f K : 5 10 1 0,92 ln 1 p 0,1 ; (2) 2) будують експериментальну залежність опору пластичній деформації lg f lge в області рівномірної деформації (фіг. 1, крива 1) [2] та експериментальні залежності опору пластичній деформації lg f lge , що характеризуються зберіганням властивості лінійності (фіг. 1, крива 1) або наявністю зламу і підвищенням кута нахилу цієї залежності в інтервалі змін міцності від дійсного напруження на границі міцності SB до величини інтенсивності напружень руйнування K зразка i (фіг. 1, крива 2). При цьому враховують необхідність заміни характеристики дійсного напруження руйнування зразка SK на характеристикуінтенсивності напружень руйнування зразка K , яка більш точно відображає напружений стан зразка при руйнуванні в умовах i концентрації напружень. Таким чином, конструкційні титанові сплави, що зберігають властивість 15 K лінійності залежності опору пластичній деформації в інтервалі змін міцності від S B до i , умовно відносять до сплавів І-ї групи, при цьому показник деформаційного зміцнення для таких I сплавів визначають як tg n n , а, конструкційні титанові сплави, що характеризуються наявністю зламу і підвищенням кута нахилу цієї залежності в інтервалі змін міцності від S B до K i , умовно відносять до сплавів II-ї групи, при цьому показник деформаційного зміцнення для II 20 II таких сплавів визначають як tg n n n . Виходячи з подібності трикутників аbс і cdk I (див. фіг. 1, крива 1), для сплавів I-ї групи має місце рівність: lg eK / ep lg K / SB i 5% lg SB / 0,2 lg 500 ep , (3) навпаки, виходячи з відсутності подібності трикутників аbс і cdk II, (див. фіг. 1, крива 2), для сплавів II-ї групи має місце нерівність: 25 lg eK / ep lg K / SB i 5% lg SB / 0,2 lg 500 ep . (4) Таким чином, групу конструкційного титанового сплаву встановлюють в залежності від співвідношення величин показників деформаційного зміцнення при деформаціях менших та більших за рівномірну, використовуючи при цьому відповідність співвідношення певних механічних характеристик даного сплаву умовам (3) або (4). 30 3) далі будують експериментальні залежності для кожної групи сплавів (фіг. 2, 3) та розраховують на їх основі емпіричні коефіцієнти: - для I-ї групи сплавів, відповідно до умов (3), будують наступну лінійну залежність (див. фіг. 2, 3, крива 1): ; (5) lg eK / ep lg K / SB i lg SB / 0,2 lg 500 ep 35 lg eK / ep lg K / SB i f lg SB / 0,2 lg 500 ep - для II-ї групи сплавів, відповідно до умов (4), будують залежність: lg eK / ep lg K / SB i f II lg SB / 0,2 lg 500 ep , (6) яка апроксимується функцією виду (див. фіг. 2, 3, крива 2): b Y f a d 1 1 X , (7) де: а = 82,23; b=82,156; с = 0,041; d=1,692 - емпіричні коефіцієнти. 5 UA 104665 C2 4) на основі залежностей (5) і (6) з урахуванням (7) визначають показники деформаційного зміцнення за формулами: - для I-ої групи сплавів: S lg B 0,2 nI n lg 500 ep 5 ; (8) - для II-ої групи сплавів: lg SB / 0,2 b II n a d lg eK / ep lg eK / ep 1 c lg 500 ep ; (9) 0,2 де: - умовна границя текучості, МПа; 1 SB B 1 p - дійсне напруження на границі міцності, МПа; B - границя міцності, МПа; 10 1 ep ln 1 p - дійсна рівномірна деформація; p - відносне рівномірне звуження, в частках; eK ln1 K - дійсна деформація після руйнування зразка; K 15 20 - відносне звуження після руйнування зразка, в частках; а = 82,23; b=82,156; с = 0,041; d=1,692 - емпіричні коефіцієнти. Результати розрахунків показників деформаційного зміцнення для деяких конструкційних титанових сплавів за формулами (8) і (9) наведені в таблиці 1, а результати оцінки точності залежностей (5) і (6), які використовують для розрахунку показників деформаційного зміцнення конструкційного титанового сплаву, наведені в таблиці 2. З таблиці 2 видно, що точність залежностей (5) і (6) достатня щодо їх використання для подальших висновків та розрахунків. Отже, за допомогою запропонованого способу, можна визначати показники деформаційного зміцнення конструкційного титанового сплаву в області нерівномірної деформації за даними лише базових механічних характеристик рівномірного звуження p 0,2 , B 30 35 K та характеристики відносного більш точно і інформативно. При цьому, отримані залежності для I 25 , II розрахунку показників деформаційного зміцнення n n і n інваріантні до різних сполучень властивостей міцності і пластичності сплавів, їх видам, режимам термічної обробки та температури випробувань. Оцінка точності розрахунку показників рівномірної деформації за запропонованим способом цілком достатня як для інженерних розрахунків, так і для наукових досліджень, що дає можливість здійснювати комплексний аналіз властивостей конструкційних титанових сплавів та більш точно оцінювати їх спроможність опиратись переходу в крихкий стан. Джерела інформації:: 1. Котречко С.А., Мешков Ю.Я., Шиян А.В. Физические основы экспресс-метода для определения хрупкой прочности конструкционных сталей // Металлофизика и новейшие технологии, 2010, т. 32, № 8, cc. 1125-1134. 2. Котречко С.А., Мешков Ю.Я., Шиян А.В., Озерский М.В. Применение экспресс-метода для определения хрупкой прочности металлических сплавов, используемых в криогенной технике // Металлофизика и новейшие технологии. - 2011, т. 33, № 3, cc. 409-416. 3. Мешков Ю.Я., Сердитова Т.Н. Разрушение деформированной стали // Киев: Наук, думка, 1989, cc. 67-72. 40 6 UA 104665 C2 Таблиця 1 № п/п Сплави 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 5 Група Tвип., K 1 ВТ16 2 ВТ16 3 ВТ22 4 ВТ6 5 2Ті-6-4 Ті+В2 6 JLCB70CD ВТ9Л 1 ВТ16 2 ВТ16 6 ВТ22 77 77 293 293 293 293 293 293 293 293 293 293 200 77 4 293 200 77 4 293 293 293 І АТ2 II ВТ5-1кт. Beta-21S 8 Ті-15-3 LCB 7 0,2 , МПа 1500 1400 1135 1286 900 1129 1448 970 980 900 1130 570 700 940 1180 770 950 1230 1365 1548 1435 1319 B , МПа 1680 1560 1240 1475 1005 1238 1679 1100 1070 960 1220 660 775 1077 1272 835 984 1325 1460 1568 1472 1397 K n nI (8) ,% 16,0 16,0 7,5 14,1 25,4 21,9 10,1 15,0 40,0 57,0 19,0 62,2 60,0 67,0 53,1 26,4 23,7 21,6 16,1 30,8 20,4 58,5 0,053 0,051 0,043 0,059 0,054 0,047 0,061 0,062 0,048 0,039 0,041 0,070 0,054 0,067 0,044 0,044 0,025 0,041 0,038 0,014 0,021 0,036 nII (9) --------0,096 0,099 0,071 0,139 0,119 0,140 0,102 0,081 0,063 0,073 0,065 0,056 0,056 0,096 Примітки: 1 - нагрів 800 °C, 1 год., охол. з піччю 500 °C, 8 год.; 2 - нагрів 800 °C, 1 год., охол. з піччю 600 °C, 8 год.; 3 - нагрів 900 °C, 0,5 год., охол. з піччю до 700 °C, 1 год., охол., повітря + 750 °C, 2 год. + 475 °C, 4 год., охол., повітря; 4 - прокатка 1050 °C; 5 - нагрів 900 °C, 0,5 год., охол. з піччю до 800 °C, 1 год., охол., повітря + 750 °C, 2 год. + 625 °C, 4 год., охол., повітря; 5 -1 нагрів 1205 °C, 4 год.; 6-10 К·с до 820 °C+300 °C, 90 хв + 450 °C, 6,5 год.; 7 - нагрів 880 °C, 10 год., охол. з піччю; 8 - нагрів 900 °C, 45 хв, охол. з піччю + 15 % CD+500 °C, 8 год. Таблиця 2 Параметр для Вибірковий Довірчий обчислення стандарт S інтервал вірогідності № Залежність залежності (5) lg eK / ep lg K / SB i lg SB / 0,2 lg 500 ep (6) lg K / SB II lg eK / ep i SB / 0,2 f lg 500 ep lg Вірогідність Р 0,012 lg K / SB i lg SB / 0,2 ±0,02 0,904 0,177 lg K / SB i lg SB / 0,2 ±0,3 0,909 10 ФОРМУЛА ВИНАХОДУ 15 Спосіб визначення показників деформаційного зміцнення конструкційного титанового сплаву, при якому проводять випробування стандартних гладких циліндричних зразків на одновісне розтягнення в інтервалі температур від 4 К до 293 К, визначають при цьому базові механічні характеристики та характеристики дійсного напруження руйнування зразка S K і відносного рівномірного звуження p , будують експериментальну залежність опору пластичній деформації lg f lge в області рівномірної деформації, який відрізняється тим, що розраховують величину 20 інтенсивності напружень руйнування зразка K , i будують експериментальні залежності опору пластичній деформації lg f lge в області нерівномірної деформації, що характеризуються зберіганням властивості лінійності або наявністю зламу і підвищенням кута нахилу цієї залежності в інтервалі змін міцності від дійсного напруження на границі міцності SB 7 UA 104665 C2 до величини інтенсивності напружень руйнування зразка K , встановлюють групу сплаву в i залежності від співвідношення величин показників деформаційного зміцнення при деформаціях менших та більших за рівномірну, додатково будують експериментальні залежності , lg eK / ep lg K / SB i f lg SB / 0,2 lg 500 ep 5 розраховують на їх основі емпіричні коефіцієнти та визначають показники деформаційного зміцнення за формулами: для I-ої групи сплавів: S lg B 0,2 , nI n lg 500 ep для II-ої групи сплавів: lg SB / 0,2 b II n a , d lg eK / ep lg eK / ep 1 c lg 500 ep де: 0,2 - умовна границя текучості, МПа, 10 1 - дійсне напруження на границі міцності, МПа, SB B 1 p B - границя міцності, МПа, 1 - дійсна рівномірна деформація, ep ln 1 p p - відносне рівномірне звуження, в частках, eK ln1 K - дійсна деформація після руйнування зразка, 15 K - відносне звуження після руйнування зразка, в частках, а = 82,23, b = 82,156, с = 0,041, d = 1,692 - емпіричні коефіцієнти. 8 UA 104665 C2 9 UA 104665 C2 Комп’ютерна верстка І. Скворцова Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 10
ДивитисяДодаткова інформація
Автори англійськоюIvasyshyn Orest Mykhailovych, Markovskyi Pavlo Yevhenovych, Kotrechko Serhii Oleksiiovych, Meshkov Yurii Yakovych, Shyian Artur Vitaliiovych
Автори російськоюИвасишин Орест Михайлович, Марковский Павел Евгеньевич, Котречко Сергей Алексеевич, Мешков Юрий Яковлевич, Шиян Артур Витальевич
МПК / Мітки
МПК: G01N 3/08, G01N 3/00, G01N 3/18
Мітки: визначення, показників, спосіб, деформаційного, зміцнення, сплаву, конструкційного, титанового
Код посилання
<a href="https://ua.patents.su/12-104665-sposib-viznachennya-pokaznikiv-deformacijjnogo-zmicnennya-konstrukcijjnogo-titanovogo-splavu.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення показників деформаційного зміцнення конструкційного титанового сплаву</a>
Попередній патент: Спосіб відновлення зношених поверхонь металевих деталей
Наступний патент: Спосіб визначення характеристики механічної стабільності конструкційних сталей
Випадковий патент: Композиція інгредієнтів для біологічно активної добавки "розум-цин"












