Спосіб вимірювання миттєвої швидкості коливань

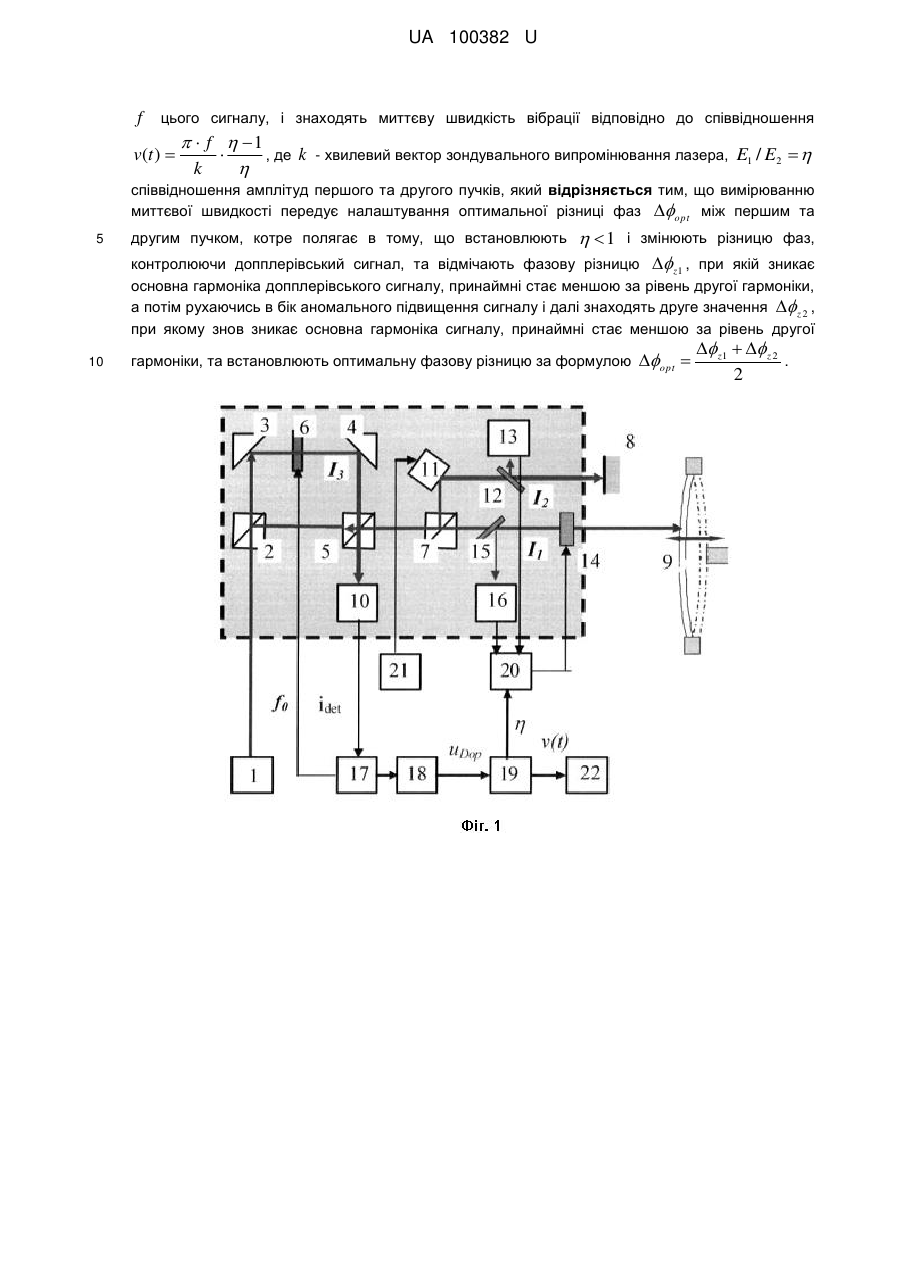
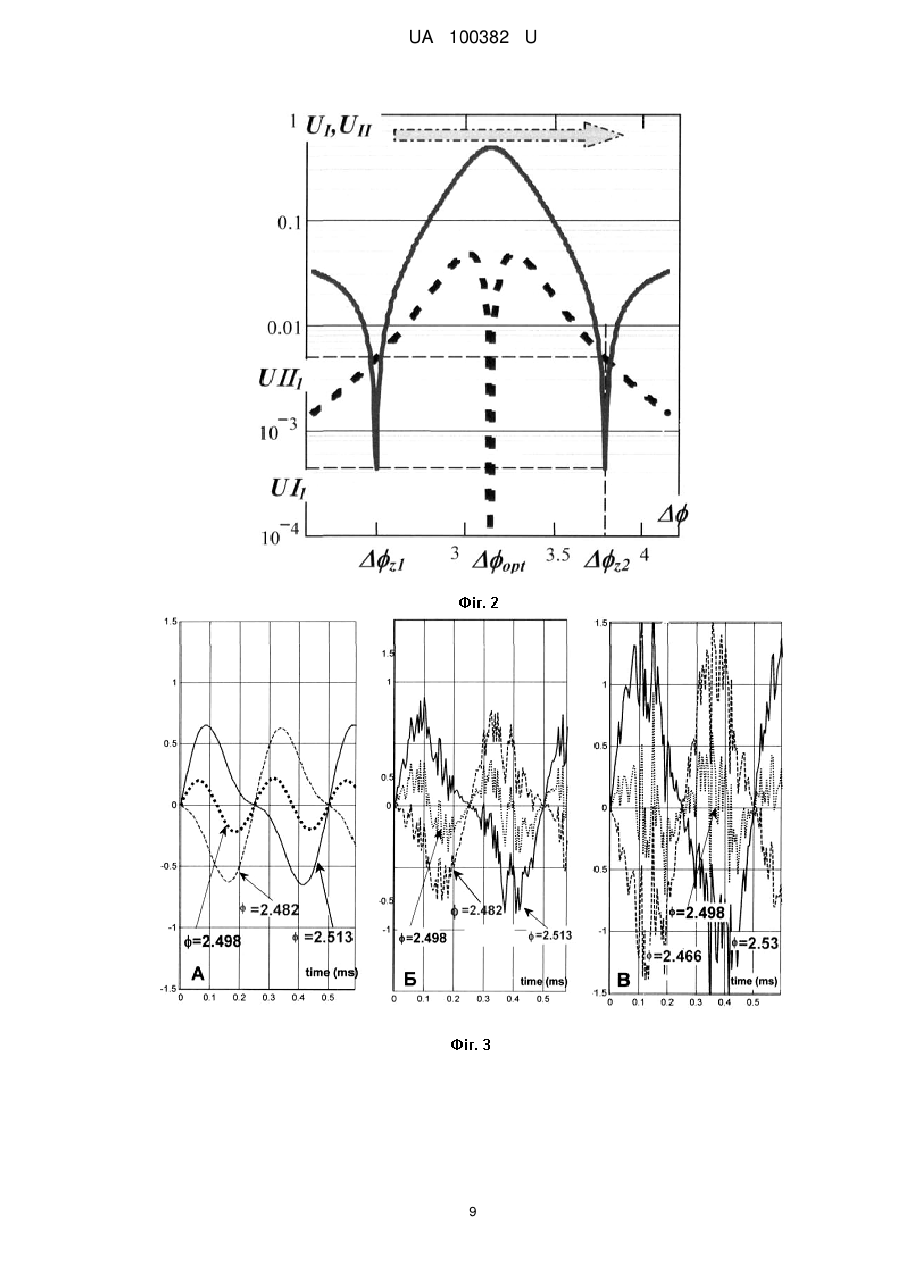
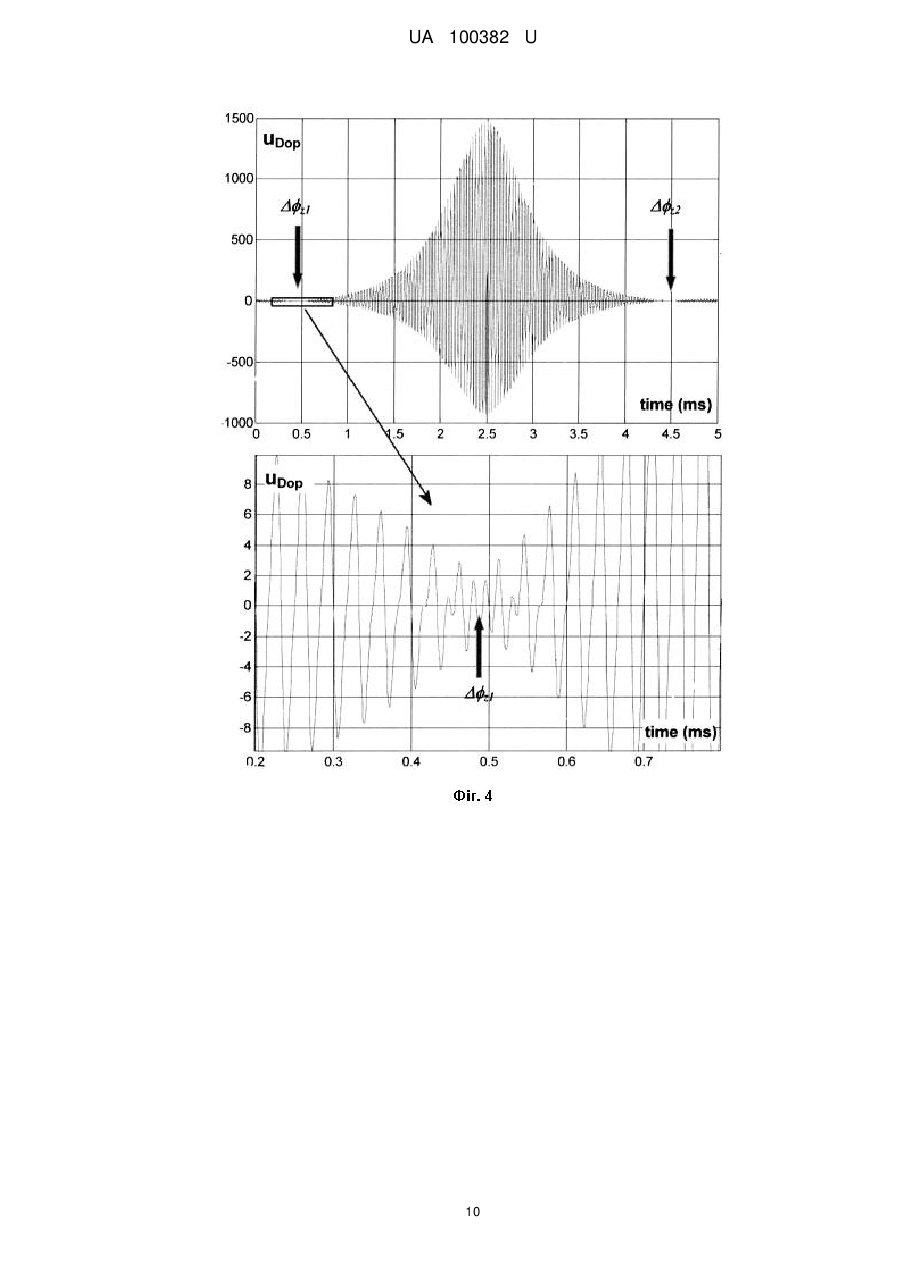
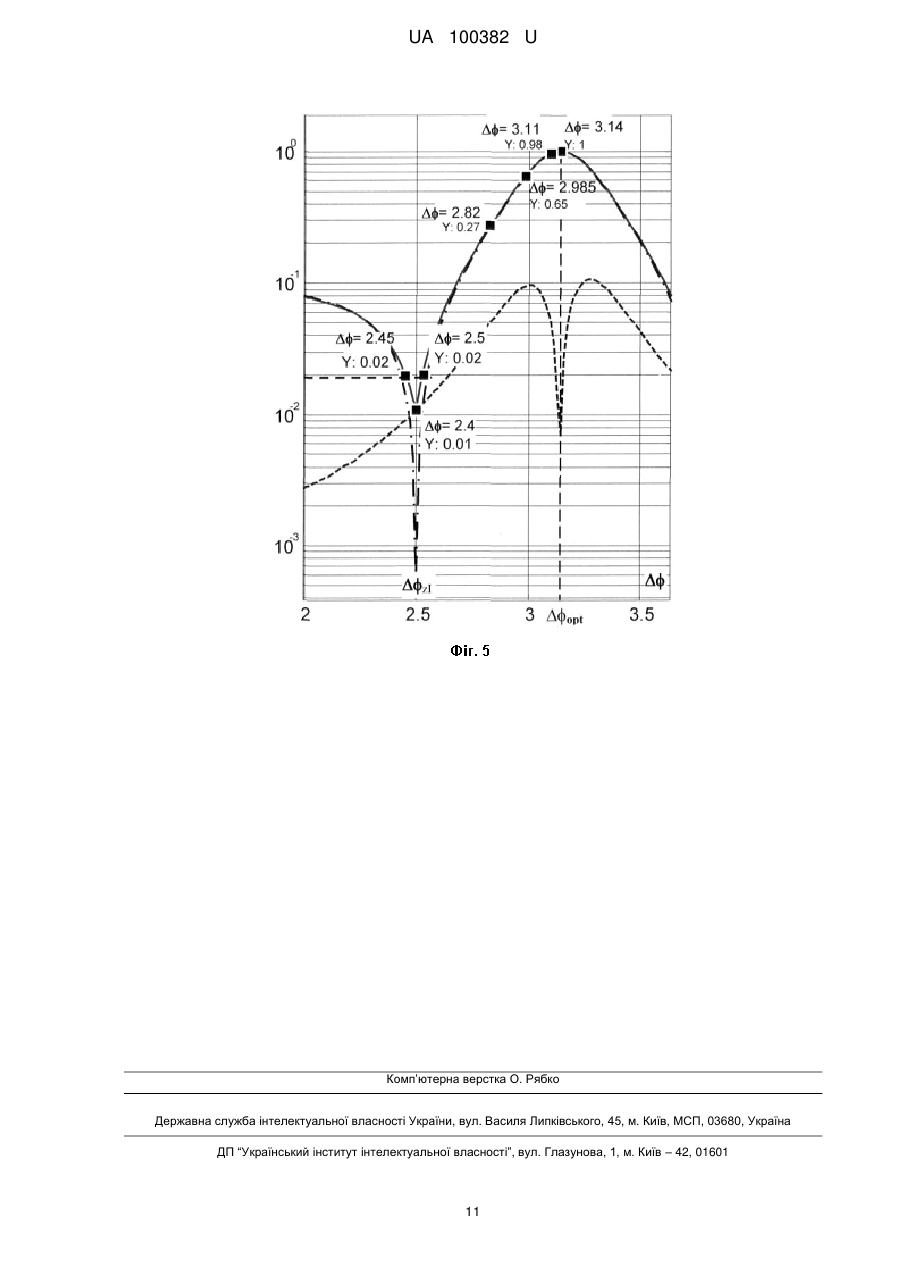
Реферат: UA 100382 U UA 100382 U 5 10 15 Корисна модель належить до контрольно-вимірювальної техніки, і може бути використана для дистанційних безконтактних вимірювань параметрів механічних коливань та вібрації, а саме миттєвої швидкості або миттєвого зміщення об'єктів та конструкції. Відомий спосіб вимірювання вібрації та пристрій для його реалізації [1], який полягає в тому, що лазерне випромінювання поділяють на два пучки, перший - зондувальний спрямовують на певну точку поверхні об'єкту, що досліджується, розсіяне об'єктом випромінювання фотодетектують разом з іншим пучком, частота якого зміщена на частоту гетеродина, а з сигналу, що детектований, виділяють складову на частоті гетеродина та виміряють його миттєву частоту. Найбільш близьким за технічною суттю до способу, що заявляється, є спосіб вимірювання миттєвої швидкості коливань [2], який полягає в тому, що лазерне випромінювання поділяють на три пучки, перший пучок спрямовують на точку поверхні об'єкту, що досліджується, розсіяне об'єктом випромінювання фотодетектують разом з другим та третім пучком, частота якого відстоїть на частоту гетеродина відносно частоти двох інших пучків, і виділяють сигнал з кутовою модуляцією в смузі частоти гетеродина, отримують миттєву частоту f цього сигналу, і знаходять миттєву швидкість вібрації відповідно до співвідношення v(t )    f  1 ,  k  де k хвилевий вектор зондувального випромінювання лазеру, E1 / E2   співвідношення амплітуд першого та другого пучків. Головний недолік найближчого аналогу це - невизначеність оптимальної різниці фаз opt 20 25 30 між першим та другим пучком та складність її точного налаштування, особливо під час проведення вимірювання. В основу корисної моделі поставлена задача зменшення похибки вимірювання миттєвої швидкості шляхом динамічного налаштування оптимальної фазової різниці під час проведення вимірювань. Поставлена задача, вирішується тим, що в способі вимірювання миттєвої швидкості коливань, який полягає в тому, що лазерне випромінювання поділяють на три пучки, перший пучок спрямовують на точку поверхні об'єкту, що досліджується, розсіяне об'єктом випромінювання фотодетектують разом з другим та третім пучком, частота якого відстоїть на частоту гетеродина відносно частоти двох інших пучків, і виділяють сигнал з кутовою модуляцією в смузі частоти гетеродина, отримують миттєву частоту f цього сигналу, і знаходять миттєву швидкість вібрації відповідно до співвідношення v(t )    f  1 ,  k  де k хвилевий вектор зондувального випромінювання лазеру, E1 / E2   співвідношення амплітуд першого та другого пучків, згідно з запропонованою корисною моделлю вимірюванню миттєвої швидкості передує налаштування оптимальної різниці фаз opt між першим та другим пучком, 35 котре полягає в тому, що встановлюють  1 і змінюють різницю фаз, контролюючи допплерівський сигнал, та відмічають фазову різницю  z1 , при якій зникає основна гармоніка допплерівського сигналу, принаймні стає меншою за рівень другої гармоніки, а потім рухаючись в бік аномального підвищення сигналу і далі знаходять друге значення  z 2 , при якому знов зникає основна гармоніка сигналу, принаймні стає меншою за рівень другої гармоніки, та 40 45 50 встановлюють оптимальну фазову різницю за формулою opt  z1  z 2 . 2 В способі, що пропонується, так само як і в найближчому аналозі, при фотодетектуванні оптичного сигналу, який відбитий об'єктом, використовується третій промінь. Наявність цього третього променя при умові оптимального налаштування параметрів віброметра спричиняє існування режиму "аномального підсилення" допплерівського сигналу, при якому суттєво підвищується чутливість до малих амплітуд коливань [3]. Таким чином, вимірюванню миттєвої швидкості передує етап встановлення оптимальних параметрів оптичної системи, зокрема різниці фаз opt між першим та другим пучком, яка повинна відповідати умові opt   . В найближчому аналозі етап встановлення оптимальної фази може бути виконано лише за умови наявності тестового сигналу з відомою амплітудою, або при свідомо стабільному за амплітудою сигналі вібрації. В останньому випадку оптимальна фаза фіксується та встановлюється як така, 1 UA 100382 U 5 10 15 20 25 30 35 40 45 50 55 при якій амплітуда вихідного сигналу досягає максимального рівня. Контроль opt під час проведення вимірювань в найближчому аналозі може виконуватись за допомогою інших вимірювальних засобів, але це суттєво ускладнює вимірювальну систему, а, за певних обставин, може стати взагалі неможливим. На відміну від найближчого аналога, в запропонованому методі визначення та налаштування opt здійснюється безпосередньо під час вимірювань і не вимагає додаткових вимірювальних засобів. Це пов'язано з тим, що значення фаз  z 2 , при яких перша гармоніка сигналу дорівнює нулю, не залежать ні від амплітуди, ні від частоти коливань. Тому для визначення оптимальної фазової різниці нема необхідності використовувати тестові коливання, або зовнішні засобі вимірювання фаз. Що стосується інших підходів для контролювання фазової різниці, котрі пропонуються в найближчому аналозі, наприклад, шляхом інтегрування миттєвої частоти [4], так цей метод, як буде показано нижче, не забезпечує достатньої точності, особливо в умовах, коли вимірювання виконуються впродовж тривалого часу і існує природній дрейф фазової різниці  . Визначення та налаштування оптимальної величини  z 2 , тим шляхом, що запропоновано в даній корисній моделі, не є очевидним та таким, що витікає з відомих інформаційних джерел, а вся сукупність ознак має над сумарний ефект, котрий призводить до неочікуваного результату, а саме, зменшення похибки вимірювання миттєвої швидкості коливань. На фігурі 1 зображено блок схему пристрою, що реалізує спосіб вимірювання параметрів вібрації. На фігурі 2 представлено залежності першої та другої гармонік сигналу віброметра як функція фазової різниці при умові   E1 / E2  1 . На фігурі 3 надано теоретичні графіки часової залежності допплерівського сигналу в окості точок  z як при наявності шумів в системі, так і при їх відсутності. А саме, Фіг. 3А - сигнал без шумів; Фіг. 3Б - середньоквадратичний рівень шумів дорівнює амплітуді другої гармоніки в точці z1 ; Фіг. 3В - середньоквадратичний рівень шумів вдвічі перевищує амплітуду другої гармоніки. На фігурі 4 надано результат симуляції допплерівського сигналу при модуляції оптичного шляху третього променя (модуляція  ). Фігура 5 подає ілюстрацію до порівняння чутливості найближчого аналога і заявленої корисної моделі. Розглянемо спосіб, що пропонується, на прикладі лазерного віброметра, блок схема якого зображена на Фіг. 1. Лазерний віброметр складається з таких елементів. Лазерний випромінювач 1 оптично зв'язаний з інтерферометром Маха-Цандера, що складається з світлоподільних елементів 2, 5 і відбиваючих дзеркал 3, 4. У одному з плеч інтерферометра, наприклад, тому, що утворено елементами 3 та 5, розміщений частотозсувний елемент 6. З світлоподільним елементом 5 оптично пов'язана світлоподільна призма (або напівпрозоре дзеркало) 7, яка є вхідним елементом іншого інтерферометра. Одне плече цього інтерферометра сформоване дзеркалом 8, а друге плече - поверхнею вібруючого об'єкта 9. Фотодетектор 10 оптично зв'язаний з світлоподільним елементом 5 прямим ходом пучка І3 і зворотнім ходом відбитого та розсіяного пучків І1 та І2. Світоподільний елемент 7 прямим та зворотнім рухом пучка І2 пов'язаний з фазомодулюючим елементом 11. Конструкція фазомодулюючого елемента 11 може бути довільною, основне його призначення - змінювати оптичний шлях пучка, залишаючи інші характеристики незмінними. Найпростіша конструкція - це керований напругою п'єзоелемент з дзеркалом. При малих переміщеннях п'єзоелемента поперечним зміщенням променя можна знехтувати. Можливі також і більш складні та досконалі модулятори фази оптичного сигналу. В цьому плечі інтерферометра також встановлений світоподільний елемент 12 та пов'язаний з ним фотодетектор 13, а світоподільний елемент 15 встановлений після світоподільного елементу 7 на оптичній осі променя І1. Елемент 15 зв'язаний зворотнім рухом пучка І1 з фотодетектором 16. В цьому плечі також по напрямку руху променя також розміщений керований фільтром нейтральної щільності 14. Важливо, щоб фільтр нейтральної щільності 12 впливав тільки на амплітуду (інтенсивність) променя, що проходить крізь нього. Цій вимозі відповідає, наприклад, рідкокришталева комірка, яка знаходиться в схрещених поляризаторах і змінює інтенсивність 2 UA 100382 U 5 10 15 20 25 30 35 40 світла при зміні напруги. Оскільки промінь проходить комірку двічі, то кінцевий стан поляризації не змінюється. Зауважимо, що керований фільтр може також розміщуватись у пучку І1. Слід зауважити, що суті корисної моделі відповідає і будь-яка інша схема розділення, формування та зведення пучків на фотодетекторі 10, що відома з інформаційних джерел, або може бути складена на підставі відомих правил. Теж саме стосується і схем відбору частини випромінювання з пучків І1 та І2 на фотодетектори 13 та 16. Інше зауваження стосується того, що суті корисної моделі відповідає також всяка оптична схема, в якій зсув оптичної частоти забезпечується в пучках І1 та І2, а частота пучка І3 залишається незмінною. Між елементом 15 та поверхнею об'єкту 9 може бути також розташована додаткова оптична система, призначення якої, наприклад, сформувати пучок для віддаленого зондування, або навпаки сфокусувати на наближеній до віброметра поверхні. Ці та подібні за призначенням оптичні системи не впливають на зміст та об'єм заявлених ознак корисної моделі. З виходом фотодетектора 10 послідовно зв'язані фільтр високих частот 17 та частотний дискримінатор 18. Частотний дискримінатор 18 може бути зібраний по любій відомій схемі, наприклад [5]. Вихідний підсилювач 19, коефіцієнт підсилення якого залежить від співвідношення амплітуд оптичних сигналів   E1 / E2 , пов'язаний з виходами частотного дискримінатора 18 та підсилювача 20. Диференційний підсилювач 20 зі змінним коефіцієнтом підсилення замикає ланцюг керування оптичною щільністю фільтра 14. Вузол 21 призначений для керування фазомодулюючим елементом 11. Його конкретне втілення залежить від конструкції фазомодулюючого елементу 11 та способу стабілізації робочої точки. В найпростішому випадку вузол 21 - це джерело напруги, що керується вручну. Цей вузол також може бути генератором пили або генератором НЧ гармонічних коливань. В схемі також передбачений прилад 22 для спостереження за сигналом віброметра, це може бути амплітудний детектор, або, найкраще, осцилоскоп, або спертаналізатор. Конкретна схема допплерівського демодулятора може включати інші елементи та вузли такі як, проміжні підсилювачі, обмежувачі, АРП, генератори проміжної частоти, змішувачі фільтри, т.і. Спосіб вимірювання миттєвої віброшвидкості має багато спільного з найближчим аналогом. Як і в найближчому аналозі світло від лазерного джерела 1 спрямовується на інтерферометр Маха-Цандера у складі світоподільних елементів 2, 5 та дзеркал 3, 4. Пучок І3 в одному із пліч інтерферометра проходить крізь акустооптичний модулятор 6, в якому до оптичної частоти додається частота гетеродина f 0 і пройшовши світоподільний елемент 5 потрапляє на фотодетектор 10. Випромінювання, що відхилене призмою 2, потрапляє у другий інтерферометр, де на світлоподільному елементі 7 поділяється на пучки І1 і І2. Пучок І1 спрямовується на точку поверхні об'єкту 9, а пучок І2 повертається назад за допомогою дзеркала 8. Оптичний шлях променя І2, може змінюватись за допомогою фазомодулюючого елемента 11. А амплітуда І1 може бути налаштована за допомогою керованого фільтру 14. Відбите (розсіяне) випромінювання від точки 9 отримує фазовий зсув, що змінюється в часі завдяки коливанню об'єкта з частотою  : Ф1 (t )  2kxmax  cos   cos(t )  1 , (1) де  k  2 /  - хвильовий вектор лазерного випромінювання, - довжина хвилі випромінювання лазера, xmax - амплітуда коливання об'єкту, 45  - кут між напрямом пучка cos( )  1 ), 1 - сталий фазовий зсув. 50 І2 та вектором переміщення об'єкта (далі будемо вважати, що Далі відбите випромінювання пучків І1 та І2 проходить у зворотному напрямку крізь елемент 7 і відхиляється світлоподільним елементом 5 на фото детектор 10, де змішуються з полем пучка пучок І3. Струм детектора 10, що є результат фотодетектування полів трьох пучків, має аналітичний вигляд: 2 2 I (t )  E12  E2  E3  2E2 E1 cos(Ф1 (t )  2 )  2E1E3 cos(2f 0t  Ф1 (t ))  2E3 E2 cos(2f 0t  2 ) , (2) 3 UA 100382 U де E1 , E2 та E3 відповідно амплітуди поля першого, другого та третього пучків на фото детекторі. Фільтр високої частоти 17 виділяє сигнал на частоті f 0 гетеродина, який описується формулою: 5 u(t )  U (t )  cos(2f 0t   (t )) , (3) де U (t ) та  (t ) - відповідно амплітуда та фаза, що змінюються повільно. Що до фази  (t ) , то вона має загальний вигляд:  E1 sin(Ф1 )  E2 sin(2 )   . (4)  E2 cos(2 )  E1 cos(Ф1 )    arctan  Сигнал u Dop (t ) на виході частотного дискримінатора 18 є пропорційним миттєвій частоті 10 f (t )  1 d  (t ) . При гармонічному коливанні (1) поверхні 9 сигнал на виході дискримінатора 2 dt 18 дорівнює [2]:   ( 2  1) u Dop (t )      xmax k 1    sin(t ) , (5) 2  2  cos(2k  xmax  cos(t )   )    1 де   E1 / E2 , а   1  2 початкова фазова різниця променів І1 та І2. Для малих амплітуд зміщення xmax   / 2 формулу (5) можна спростити: 15  cos( )   kX ( 2  1) sin( ) cos(t )  . (6) u Dop (t )  2kxmax 1 sin(t )    1  2 2 2 cos( )  ( 2  1)  2 cos( )  (  1)      Очевидно, що формула (6) подає допплерівський сигнал, як суму першої та другої гармонік. Їх амплітуди записані нижче: U I    202kxmax (cos( )   ) k 2 X 12 ( 2  1) sin( ) . (7) U II    2 2 cos( )  ( 2  1) 2 cos( )  ( 2  1)   При умові opt    2  n ( n - ціле або нуль) друга гармоніка зникає формула для амплітуди основної гармоніки отримує вигляд: u Dop (t )  2  vmax k  sin(t )  де   1 або u Dop (t )  2k  v(t )    1 , (8) v(t )  vmax sin(t ) - миттєва швидкість, a vmax - її амплітуда. Якщо порівняти формулу (8) з сигналом класичного лазерного допплерівського віброметру uDop, 2 x (t )  2vmax k  sin(t ) [1], то бачимо, що в лазерному віброметрі з трьома 25 інтерферуючими променями виникає "аномальне підсилення" допплерівського сигналу, що дорівнює    1 . В певних випадках, наприклад, в схемі [6] це "підсилення" може бути використано для покращення співвідношення сигнал/шум. Остаточно для миттєвої швидкості коливань отримуємо формулу: v(t )  30 u Dop (t )   1 2k  . (9) Або, якщо сигнал u Dop (t ) на виході частотного дискримінатора 18 відкалібрований в одиницях частоти, тобто коефіцієнт пропорційності між u Dop (t ) одиницю, співвідношення (9) приймає вигляд: v(t )    f   1 . (10)  k  4 та 2  f (t ) становить UA 100382 U Підсилювач 19 масштабує сигнал u Dop з виходу частотного дискримінатора відповідно з 5 10 15 заданим значенням величини  , для отримання миттєвого значення швидкості вібрації v(t ) . Для стабілізації відношення амплітуд пучків І2 та І3 на заданому рівні  призначений диференційний підсилювач 20. При зміні амплітуди пучка І2, що може трапляється під час вимірювань, відповідно змінюється і напруга на виході підсилювача 20. Ця напруга керує щільністю фільтра 14, в такий спосіб, що її підвищення вище певного рівня, котрий пов'язаний з величиною  , спричиняє зменшення оптичного пропускання фільтра і навпаки. Таким чином, від'ємний зворотній зв'язок системи керування фільтром стабілізує відношення амплітуд   E1 / E2 поблизу заданого рівня  . "Аномальне підсилення"  в повній мірі виникає при встановленні оптимальної фазової opt   . Налаштування оптимальної різниці фази в даній корисній моделі має суттєві відмінності від найближчого аналога. А саме. Спочатку за допомогою фільтра 14 встановлюється параметр   1 , наприклад  z  0.8 . Після цього змінюють оптичний шлях додаткового опорного променя і візуально спостерігають форму сигналу на осцилоскопі 22. На Фіг. 2 зображено залежності амплітуди першої та другої гармонік, як функція фазової різниці (для бачити з Фіг. 2 існують дві точки   0.8 , xmax  6nm, k  2   z , в яких амплітуда основної гармоніки дорівнює нулю, принаймні амплітуда першої гармоніки менша за амплітуду другої відповідають рішенню рівняння 20 z    arccos( ) . (11) U I ( )  0 (7): Зауважимо, що дійсне рішення 25 30 35 40  0.01nm 1 ). Як можна U Iz  U IIz . Ці точки  z існує лише для   1 . Змінюючи оптичний шлях променя за допомогою комірки 11 знаходять першу точку  z1 , при якій спостерігається зникнення основної гармоніки. Під фразою "зникненням основної гармоніки" треба розуміти, що її амплітуда стає меншою за рівень шумів. Якщо ж шуми в системі віброметра незначні, то, як видно з Фіг. 2 в точці (в нашому випадку z1    cos( z )  2.498 ), де зникає перша гармоніка залишається сигнал другої гармоніки, який може бути зафіксований при достатній чутливості приладів. Графіки на Фіг. 3, що побудовані на підставі співвідношення (5) ілюструють сказане вище. Суцільні лінії на всіх трьох графіках відповідають випадкам    z1 , точкові лінії відповідають    z1 , а перервна лінія відповідає умові    z1 . Графік на Фіг. 3А побудований за умови відсутності шумів в системі, принаймні вони значно менші ніж амплітуда другої гармоніки, а графіки на Фіг. 3Б та Фіг. 3В при умові, що середньоквадратичний рівень шумів відповідно рівний та вдвічі перевищує амплітуду другої гармоніки. Як видно з наведених даних, при відсутності шумів та при їх середньоквадратичному рівну, який не перевищує амплітуди другої гармоніки, точка  z1 надійно визначається в діапазоні 0.03 радіан, а при шумах, що вдвічі перевищують амплітуду другої гармоніки, діапазон надійного визначення  z1 слід збільшити вдвічі. Після фіксації точки  z1 змінюють оптичний шлях зондувального променю в напрямку значного росту сигналу (на Фіг. 2 це показано суцільною сірою стрілкою з перервним контуром). Після подолання максимуму сигналу, амплітуда основної гармоніки знов починає зменшуватись і зникає в точці z 2    cos( z )  3.785 . Очевидно, що оптимальна фазова різниця 1 opt   знаходиться точно посередині між z1 та  z 2 , а саме: opt  ( z 2   z1 ) . 2 Зазначимо, що для визначення opt нема необхідності вираховувати поточні фазові 45 різниці на підставі зміни оптичних шляхів: треба просто встановити оптичний шлях додаткового 5 UA 100382 U променя точно посередині між виміряннями "1" та "2" і фазова різниця автоматично стане opt   . Ще одне важливе зауваження полягає в тому, що розміщення точок залежить ні від частоти, ні від амплітуди (в межах 5 10  z на осі  не xmax   / 2 ) коливань. Це безпосередньо випливає з вигляду корнів (11) формули (7) для амплітуди першої гармоніки допплерівського сигналу U I ( ) . Таким чином, налаштування фази можливо виконувати безпосередньо під час експерименту, аналізуючи спектральний склад досліджуваного сигналу вібрації! Процес налаштування фази може бути певною мірою автоматизований. Для цього на фазомодулюючу комірку 11 подають напругу, що змінюється за гармонічним законом Ф2  m  cos(modt ) , де  mod - частота модуляції, a m - індекс модуляції. Для одночасного визначення обох значень  z1, 2 індекс модуляції повинен задовольняти умові 15 В цьому випадку максимальне значення допплерівського сигналу u Dop (t ) буде відповідати сигналу при оптимальному "підсиленні", котрий описується формулами (8-9). Графік на Фіг. 4, котрий наданий в координатах напруга на виході частотного дискримінатора, пропорційна миттєвій допплерівській частоті, як функція часу, відповідає саме такому випадку. Графік побудовано за формулою (5) при умові повільної зміни (   mod ) фазової різниці з індексом m  0.68 . Параметри симуляції такі:  0.5nm,  0.8 . На графіку відмічені точки фазової модуляції   2  0.1kHz, mod  2  30kHz, xmax 20 m  z 2  z1 . модуляції, при яких сигнал досягає мінімуму. А для того, щоб наглядно продемонструвати подвоєння частоти допплерівського сигналу в окості точки  z1 на нижній частині Фіг. 4 зображено збільшений фрагмент залежності u Dop (t ) . Точки мінімуму допплерівського сигналу це - z1  2.5rad та z 2  3.8rad , але розраховувати ці значення нема необхідності: треба лише за допомогою комірки 11 встановити таку оптичну затримку, щоб фазова різниця відповідала величині opt  25 30 35 40 45 1 ( z 2   z1 ) . 2 Взагалі, якщо амплітуда сигналу змінюється повільно відносно частоти модуляції, тоді замість підлаштовувати оптичної схеми для встановлення opt досить вимірювати максимальне значення амплітуди, яке автоматично буде дорівнювати такому за формулами (8). Порівняємо характеристики пристрою, що реалізує заявлений спосіб, з найближчим аналогом. Нагадаємо, що в найближчому аналозі пропонують три підходи для встановлення оптимальної фазової різниці. По-перше, оптимальна фазова різниця задається перед початком вимірювань, та розглядається як незмінна. По-друге, вимірювання поточної фазової різниці забезпечується додатковими засобами і на підставі отриманих даних виконується корекція opt . Третій шлях - це використання додаткового ланцюга спостереження з інтегратором сигналу. Такий метод може бути достатньо ефективним лише при незмінній амплітуді сигналу вібрації, принаймні якщо середня швидкість флуктуацій амплітуди менша за сталу ланцюга спостереження. Якщо амплітуда вібрації змінюється зі швидкістю меншою, ніж стала інтегратора, тоді ланцюг спостереження буде інтерпретувати зміну (головним чином зменшення) вихідного сигналу інтегратора, як зменшення "аномального" підсилення, тобто відхилення фази від точки opt і буде намагатися змінити оптичний шлях, вносячи таким чином свідому помилку. Таким чином, в найближчому аналозі не передбачено повній мірі засобів для надійного встановлення оптимальної фазової різниці, особливо у випадках, коли вимірювання виконуються впродовж тривалого часу і неможливо додатковими засобами визначити дрейф оптичних шляхів хвиль, що інтерферують на фотодетекторі. Щоб оцінити помилку, пов'язану з невизначеністю різниці фаз в найближчому аналозі, задамо дві величини дрейфу фазової різниці, наприклад,  old1  0,05 , та  old 2  0,1 та розрахуємо відповідні помилки у вимірюванні допплерівського сигналу. 6 UA 100382 U На графіку Фіг. 5 зображені нормовані на максимальне значення амплітуди допплерівського сигналу u Dop ( ) (суцільна лінія), першої гармоніки (перервна з точкою лінія, та другої гармоніки (перервна лінія) для параметрів сигналу 5  z  0.8, xmax  3.15nm, k  2   0.01nm 1 . Графіки для гармонік - це аналітичне рішення за формулою (5). А що стосується залежності u Dop ( ) , то слід зазначити, що безпосередньо застосовувати формулу (3) некоректно, оскільки при різних  амплітудне значення сигналу (тобто його максимум) досягається для різних фазових кутів 10   t . методів. Як видно з Фіг. 5, розрахунки відносних помилок виміряних амплітуд при наявності похибки визначення фазової різниці  дають наступні результати: U Dop (opt   old1 ) U Dop (opt ) U Dop (opt   old 2 ) U Dop (opt ) 15 Тому графік u Dop ( ) отриманий за допомогою числових   U Dop (opt   old1 ) U Dop (opt ) U Dop (opt   old 2 ) U Dop (opt )  0.65 ,  0.27 . Для порівняння похибки визначення амплітуди сигналу методом, що пропонується, задамо достатньо високий середньоквадратичний рівень завад наприклад, такий, що вдвічі перевищує амплітуду другої гармоніки в точці  z : U n  2U IIz . (Фіг. 3В). Пунктирна лінія на Фіг. 5, що відповідач цій величині, проходить на рівні 0.02. Відповідно невизначеність фази  new    zI складає 2.5  2.45  0.025 . 2 Розрахуємо, якій похибці вимірювання допплерівського сигналу буде відповідати невизначеність  new при встановлені оптимальної фазової різниці. Як можна бачити з Фіг. 5, 20 25 30 35 40  new від opt призводить до похибки визначення миттєвої швидкості в 2 %. При середньоквадратичному рівні шумів, який дорівнює амплітуді другої гармоніки (рівень 0.01 на Фіг. 5, графіки сигналів на Фіг. 3Б), похибка вимірювання допплерівського сигналу через невизначеність оптимальної фазової різниці буде менша за 1 %. Таким чином, прилад, що реалізує запропонований метод, дозволяє уникнути додаткових засобів стабілізації фазової різниці, або зменшити похибку вимірювання допплерівського сигналу (миттєвої швидкості вібрації) у 3,5 рази та більше. відхилення Джерела інформації: 6 1. Патент США № 5394233 МПК G01 С3/00, В 9/02, 1995. 2. Патент України № 94564 МПК G01С 3/02. Яровой Л.К. "Спосіб вимірювання миттєвої віброшвидкості". заяв. 18.11.2010. чинній від 10.05.2011, друк. 10.05.2011. Бюл. № 24-4с: іл. 3. Яровой Л.К. Особливості роботи лазерного допплерівського віброметра з трихвилевим фотозмішуванням в нанометровому діапазоні.// Вісник Київського університету. Серія: Математика. Механіка. 2011 - Випуск. 26. - С. 39-43. 4. Справочник по учебному проектированию приемно-усилительных устройств, под ред. М.К. Белкина, "Выща школа", Киев, 1988, 472 с. 5. L.Е. Drain, The Laser Doppler Technique, John Wiley & Son Ltd., New York, 1980. 6. Патент України № 990558 МПК G01C 3/02. Яровой Л.К, Іващенко Д.О., Розумнюк B.I "Лазерний допплерівський вимірювач вібрації". заяв. 18.11.2010. чинній від 10.07.2012, друк. 10.07.2012. Бюл. № 13-5с: іл ФОРМУЛА КОРИСНОЇ МОДЕЛІ 45 Спосіб вимірювання миттєвої швидкості коливань, який полягає в тому, що лазерне випромінювання поділяють на три пучки, перший пучок спрямовують на точку поверхні об'єкту, що досліджується, розсіяне об'єктом випромінювання фотодетектують разом з другим та третім пучком, частота якого відстоїть на частоту гетеродина відносно частоти двох інших пучків, і виділяють сигнал з кутовою модуляцією в смузі частоти гетеродина, отримують миттєву частоту 7 UA 100382 U f цього сигналу, і знаходять миттєву швидкість вібрації відповідно до співвідношення v(t )    f  1 , де k  k  - хвилевий вектор зондувального випромінювання лазера, E1 / E2   співвідношення амплітуд першого та другого пучків, який відрізняється тим, що вимірюванню миттєвої швидкості передує налаштування оптимальної різниці фаз opt між першим та 5 другим пучком, котре полягає в тому, що встановлюють  1 і змінюють різницю фаз, контролюючи допплерівський сигнал, та відмічають фазову різницю  z1 , при якій зникає основна гармоніка допплерівського сигналу, принаймні стає меншою за рівень другої гармоніки, а потім рухаючись в бік аномального підвищення сигналу і далі знаходять друге значення  z 2 , при якому знов зникає основна гармоніка сигналу, принаймні стає меншою за рівень другої 10 гармоніки, та встановлюють оптимальну фазову різницю за формулою opt   z1   z 2 . 2 UA 100382 U 9 UA 100382 U 10 UA 100382 U Комп’ютерна верстка О. Рябко Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 11