Пристрій для арифметичного та алгебраїчного порівняння двох чисел класу лишків
Номер патенту: 92069
Опубліковано: 25.07.2014
Автори: Кошман Сергій Олександрович, Янко Аліна Сергіївна, Краснобаєв Віктор Анатолійович
Формула / Реферат
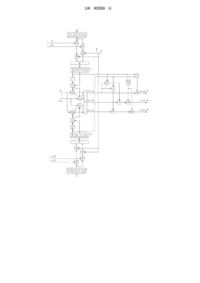
Пристрій для арифметичного та алгебраїчного порівняння двох чисел класу лишків (КЛ), що містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший, другий і третій елементи І, перший і другий елементи АБО, перший, другий та третій елементи заборони, суматор за модулем два, при цьому перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, до перших входів першого та другого суматорів підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені відповідні шини подачі констант виду ![]() (
(![]() ; де
; де ![]() - модулі КЛ;
- модулі КЛ; ![]() - кількість модулів КЛ;
- кількість модулів КЛ; ![]() ), а виходи суматорів першої та другої груп підключено відповідно до перших і других груп входів схеми порівняння однорядкового коду (СПОК), виходи першого та другого елементів І підключено до перших входів відповідно першого та другого елементів АБО, вихід суматора за модулем два підключено до першого (забороненого) входу першого елемента заборони, виходи першого та другого елементів АБО підключено до перших (інформаційних) входів відповідно другого та третього елементів заборони, вихід третього елемента І підключено до других (заборонених) входів відповідно другого та третього елементів заборони, який відрізняється тим, що введено третій, четвертий, п'ятий і шостий суматори, першу, другу, третю і четверту групи елементів І, першу і другу групи елементів АБО, перший і другий прийомні регістри, при цьому вихід першого вхідного регістра підключено до перших входів елементів І першої та другої груп, а вихід другого вхідного регістра підключено до перших входів елементів І третьої та четвертої груп, перша шина додатної ознаки підключена до других входів елементів І першої групи, а друга шина додатної ознаки підключена до других входів елементів І третьої групи, перша шина від'ємної ознаки підключена до других входів елементів І другої групи, а друга шина від'ємної ознаки підключена до других входів елементів І четвертої групи, виходи елементів І першої та другої груп підключено до перших входів відповідно третього та четвертого суматорів, виходи яких через елементи АБО першої групи підключено до входу першого прийомного регістра, а виходи елементів І третьої та четвертої груп підключено до перших входів відповідно п'ятого та шостого суматорів, виходи яких через елементи АБО другої групи підключено до входу другого прийомного регістра, виходи першого та другого прийомних регістрів підключено до других входів відповідно першого та другого суматорів, вихід підрегістра лишку
), а виходи суматорів першої та другої груп підключено відповідно до перших і других груп входів схеми порівняння однорядкового коду (СПОК), виходи першого та другого елементів І підключено до перших входів відповідно першого та другого елементів АБО, вихід суматора за модулем два підключено до першого (забороненого) входу першого елемента заборони, виходи першого та другого елементів АБО підключено до перших (інформаційних) входів відповідно другого та третього елементів заборони, вихід третього елемента І підключено до других (заборонених) входів відповідно другого та третього елементів заборони, який відрізняється тим, що введено третій, четвертий, п'ятий і шостий суматори, першу, другу, третю і четверту групи елементів І, першу і другу групи елементів АБО, перший і другий прийомні регістри, при цьому вихід першого вхідного регістра підключено до перших входів елементів І першої та другої груп, а вихід другого вхідного регістра підключено до перших входів елементів І третьої та четвертої груп, перша шина додатної ознаки підключена до других входів елементів І першої групи, а друга шина додатної ознаки підключена до других входів елементів І третьої групи, перша шина від'ємної ознаки підключена до других входів елементів І другої групи, а друга шина від'ємної ознаки підключена до других входів елементів І четвертої групи, виходи елементів І першої та другої груп підключено до перших входів відповідно третього та четвертого суматорів, виходи яких через елементи АБО першої групи підключено до входу першого прийомного регістра, а виходи елементів І третьої та четвертої груп підключено до перших входів відповідно п'ятого та шостого суматорів, виходи яких через елементи АБО другої групи підключено до входу другого прийомного регістра, виходи першого та другого прийомних регістрів підключено до других входів відповідно першого та другого суматорів, вихід підрегістра лишку ![]() за найменшим модулем
за найменшим модулем ![]() КЛ першого прийомного регістра одночасно підключено до входу першого блока констант нулевізації, до першого входу першого елемента І, до першого входу третього елемента І, а також підключено до першого входу суматора за модулем два, а вихід підрегістра лишку
КЛ першого прийомного регістра одночасно підключено до входу першого блока констант нулевізації, до першого входу першого елемента І, до першого входу третього елемента І, а також підключено до першого входу суматора за модулем два, а вихід підрегістра лишку ![]() за найменшим модулем
за найменшим модулем ![]() КЛ другого прийомного регістра одночасно підключено до входу другого блока констант нулевізації, до першого входу другого елемента І, до другого входу третього елемента І, а також підключено до другого входу суматора за модулем два, шина подачі значення
КЛ другого прийомного регістра одночасно підключено до входу другого блока констант нулевізації, до першого входу другого елемента І, до другого входу третього елемента І, а також підключено до другого входу суматора за модулем два, шина подачі значення ![]()
![]() підключена до других входів третього, четвертого, п'ятого та шостого суматорів, перший
підключена до других входів третього, четвертого, п'ятого та шостого суматорів, перший ![]() вихід СПОК підключено до других входів першого та другого елементів І, також до другого (інформаційного) входу першого елемента заборони, вихід якого є першим
вихід СПОК підключено до других входів першого та другого елементів І, також до другого (інформаційного) входу першого елемента заборони, вихід якого є першим ![]() виходом пристрою, другий
виходом пристрою, другий ![]() вихід СПОК підключено до другого входу першого елемента АБО, третій
вихід СПОК підключено до другого входу першого елемента АБО, третій ![]() вихід СПОК підключено до другого входу другого елемента АБО, виходи другого та третього елементів заборони є відповідно другим
вихід СПОК підключено до другого входу другого елемента АБО, виходи другого та третього елементів заборони є відповідно другим ![]() і третім
і третім ![]() виходами пристрою.
виходами пристрою.
Текст
Реферат: Пристрій для арифметичного та алгебраїчного порівняння двох чисел класу лишків (КЛ), що містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший, другий і третій елементи І, перший і другий елементи АБО, перший, другий та третій елементи заборони, суматор за модулем два. Введено третій, четвертий, п'ятий і шостий суматори, першу, другу, третю і четверту групи елементів І, першу і другу групи елементів АБО, перший і другий прийомні регістри. UA 92069 U (12) UA 92069 U UA 92069 U 5 10 15 20 25 30 35 40 45 Корисна модель (пристрій) належить до області автоматики та обчислювальної техніки і може бути застосована в інформаційно-телекомунікаційних системах і мережах, що функціонують у непозиційній системі числення класу лишків (КЛ). Відомий пристрій (аналог) для порівняння чисел, що містить перший і другий вхідні регістри, перший і другий блоки констант, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, елементи І, АБО, групу ключових елементів та ін. (А.с. СССР № 618739, МПК G06F 7/04,1976 р.). Недолік даного аналога - низькі функціональні можливості пристрою. Це обумовлено тим, що пристрій не здатний виконувати операцію алгебраїчного порівняння двох чисел КЛ. Також відомий пристрій (аналог) (А.с. СССР № 608155, МПК G06F 7/04, 1976 р.), що містить перший і другий вхідні регістри, перший і другий блоки констант, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, елементи І, АБО та ін. Недолік даного аналога - низькі функціональні можливості пристрою. Це обумовлено тим, що пристрій не здатний виконувати операцію алгебраїчного порівняння двох чисел КЛ. Близьким за технічною суттю до запропонованої корисної моделі (аналогом) є пристрій (А.с. СССР № 1037244, МПК G06F 7/04, 1983р., БВ № 31), де реалізується операція порівняння двох чисел КЛ. Пристрій для порівняння чисел класу лишків містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації (БКН), перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду (СПОК), причому перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп до других входів яких підключені шини подачі констант, виходи суматорів першої та другої груп підключено до перших і других входів СПОК. Недолік даного аналога - низькі функціональні можливості пристрою. Це обумовлено тим, що пристрій не здатний виконувати операцію алгебраїчного порівняння двох чисел КЛ. Близьким за технічною суттю до запропонованої корисної моделі (аналогом) є пристрій для арифметичного порівняння чисел КЛ (Патент України на корисну модель № 64973, МПК G06F 7/04 (2006. 01), дата публікації 25.11.2011, Бюл. № 22). Пристрій містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, елементи І, елементи АБО. Недолік даного аналога - низькі функціональні можливості пристрою. Це обумовлено тим, що пристрій не здатний виконувати операцію алгебраїчного порівняння двох чисел КЛ. Близьким за технічною суттю до запропонованої корисної моделі (аналогом) є пристрій для порівняння даних, що представлені у КЛ (патент України на корисну модель № 73379 України, МПК (2006.01) G06F 7/04. Опубл. 25.09.2012, Бюл. № 18). Пристрій містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший і другий елементи І, перший, другий та третій елемент АБО, елемент заборони, при цьому, перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені відповідні шини подачі констант виду 0, m1, 2 m1,..., N 1 m1 ( N 50 55 n m i ; де i 2 m i - модулі КЛ; n - кількість модулів КЛ; mi mi1 ), а виходи суматорів першої та другої груп підключено відповідно до перших і других груп входів схеми порівняння однорядкового коду. Недолік аналога - низькі функціональні можливості пристрою. Це обумовлено тим, що пристрій не здатний виконувати операцію алгебраїчного порівняння двох чисел КЛ. Найбільш близьким за технічною суттю до запропонованої корисної моделі (прототипом) є пристрій для порівнянні даних, що представлені у непозиційній системі числення класу лишків, (патент України на корисну модель № 79587 України, МПК (2006.01) G06F 7/04. Заявка № u 2012 12654. Заявл. 05.11.2012. Опубл. 25.04.2013, Бюл. № 8. - 9 с.). Пристрій містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший і другий елементи І, перший і другий елементи АБО, перший елемент заборони, суматор за модулем два, другий та третій елементи заборони, третій елемент І, при цьому, перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних 1 UA 92069 U регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені 5 10 15 20 25 30 35 40 відповідні шини подачі констант виду 0, m1, 2 m1,..., N 1 m1 ( N 50 m i - модулі КЛ; n i 2 кількість модулів КЛ; mi mi1 ), а виходи суматорів першої та другої груп підключено відповідно до перших і других груп входів схеми порівняння однорядкового коду, перший nA nB вихід схеми порівняння однорядкового коду підключено до перших входів першого та другого елементів І та до першого (інформаційного) входу першого елемента заборони, вихід якого є першим A B виходом пристрою, другий n A nB вихід схеми порівняння однорядкового коду підключено до першого входу першого елемента АБО, третій n A nB вихід схеми порівняння однорядкового коду підключено до першого входу другого елемента АБО, вихід підрегістра лишку a1 за найменшим модулем m1 КЛ першого регістра одночасно підключено до входу першого блока констант нулевізації та до другого входу першого елемента І, а вихід підрегістра лишку b1 за найменшим модулем m1 КЛ другого регістра одночасно підключено до входу другого блока констант нулевізації та до другого входу другого елемента І, а виходи першого та другого елементів І підключено до других входів відповідно першого та другого елементів АБО, вихід підрегістра лишку b1 за найменшим модулем m1 КЛ першого регістра підключено до першого входу третього елемента І та до першого входу суматора за модулем два, вихід якого підключено до другого (забороненого) входу першого елемента заборони, а вихід підрегістра лишку b1 за найменшим модулем m1 КЛ другого регістра підключено до другого входу третього елемента І та до другого входу суматора за модулем два, виходи першого та другого елементів АБО підключено до перших (інформаційних) входів відповідно другого та третього елементів заборони, вихід третього елемента І підключено до других (заборонених) входів відповідно другого та третього елементів заборони, виходи яких є відповідно другим A B і третім A B виходами пристрою. Недолік прототипу - низькі функціональні можливості пристрою. Це обумовлено тим, що пристрій не здатний виконувати операцію алгебраїчного порівняння двох чисел КЛ. Технічною задачею (метою) запропонованої корисної моделі є розширення функціональних можливостей пристрою-прототипу. Розширення функціональних можливостей пристроюпрототипу обумовлюється забезпеченням запропонованим пристроєм, крім виконання їм операції арифметичного порівняння, додатково виконання також і операції алгебраїчного порівняння двох чисел КЛ. Поставлена задача вирішується наступним чином. У пристрій для арифметичного та алгебраїчного порівняння двох чисел класу лишків (КЛ), що містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший, другий і третій елементи І, перший і другий елементи АБО, перший, другий та третій елементи заборони, суматор за модулем два, при цьому, перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, до перших входів першого та другого суматорів підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені відповідні шини подачі констант виду 0, m1, 2 m1,..., N 1 m1 ( N 45 n m i ; де n m i ; де i2 m i - модулі КЛ; n - кількість модулів КЛ; mi mi 1 ), а виходи суматорів першої та другої груп підключено відповідно до перших і других груп входів схеми порівняння однорядкового коду (СПОК), виходи першого та другого елементів І підключено до перших входів відповідно першого та другого елементів АБО, вихід суматора за модулем два підключено до першого (забороненого) входу першого елемента заборони, виходи першого та другого елементів АБО підключено до перших (інформаційних) входів відповідно другого та третього елементів заборони, вихід третього елемента І підключено до перших (заборонених) входів відповідно другого та третього елементів заборони, введено третій, четвертий, п'ятий і шостий суматори, першу, другу, третю і четверту групи елементів І, першу і другу групи елементів АБО, перший і другий прийомні регістри, при цьому, вихід першого 2 UA 92069 U 5 10 15 20 25 30 вхідного регістра підключено до перших входів елементів І першої та другої груп, а вихід другого вхідного регістра підключено до перших входів елементів І третьої та четвертої груп, перша шина додатної ознаки підключена до других входів елементів І першої групи, а друга шина додатної ознаки підключена до других входів елементів І третьої групи, перша шина від'ємної ознаки підключена до других входів елементів І другої групи, а друга шина від'ємної ознаки підключена до других входів елементів І четвертої групи, виходи елементів І першої та другої груп підключено до перших входів відповідно третього та четвертого суматорів, виходи яких через елементи АБО першої групи підключено до входу першого прийомного регістра, а виходи елементів І третьої та четвертої груп підключено до перших входів відповідно п'ятого та шостого суматорів, виходи яких через елементи АБО другої групи підключено до входу другого прийомного регістра, виходи першого та другого прийомних регістрів підключено до других входів відповідно першого та другого суматорів, вихід підрегістра лишку a1 за найменшим модулем m1 КЛ першого прийомного регістра одночасно підключено до входу першого блока констант нулевізації, до першого входу першого елемента І, до першого входу третього елемента І, а також підключено до першого входу суматора за модулем два, а вихід підрегістра лишку b1 за найменшим модулем m1 КЛ другого прийомного регістра одночасно підключено до входу другого блока констант нулевізації, до першого входу другого елемента І, до другого входу третього елемента І, а також підключено до другого входу суматора за модулем два, n шина подачі значення M / 2 M m i підключена до других входів третього, четвертого, i 1 п'ятого та шостого суматорів, перший nA nB вихід СПОК підключено до других входів першого та другого елементів І, також до другого (інформаційного) входу першого елемента заборони, вихід якого є першим A B виходом пристрою, другий nA nB вихід СПОК підключено до другого входу першого елемента АБО, третій nA nB вихід СПОК підключено до другого входу другого елемента АБО, виходи другого та третього елементів заборони є відповідно другим A B і третім A B виходами пристрою. В цьому випадку введення вказаних ознак дозволяє досягти мету запропонованої корисної моделі. Тобто, забезпечити виконання як операції арифметичного, так і алгебраїчного порівняння двох чисел А і В у КЛ. При цьому в даній корисній моделі реалізується наступний алгоритм порівняння двох чисел КЛ ; A B, якщо n A nB a1 b1 0mod 2 A B, якщо n A nB n A nB a1 1 b1 0 ; (1) A B, якщо n n n n b 1 a 0 . A B A B 1 1 При цьому маємо, що M A B 2 A B , якщо A B 0, A B M A B , якщо A B 0, 2 (2) тобто, для додатних чисел маємо A M A , а для від'ємних - A M A . Крім цього при 2 2 визначенні результату операції порівняння двох чисел КЛ використовуються наступні явні (див. (2)) та прості співвідношення: якщо A B, тоді A B, (3) якщо A B, тоді A B, 35 40 якщо A B, тоді A B.На кресленні (лист 1, 2) представлена блок-схема корисної моделі. В таблиці 1 представлена таблиця кодових слів для КЛ, що задано основами m1 2 , m2 3 і m3 5 . В таблиці 2 представлено вміст БКН 7 і 8 для КЛ при m1 2 . В таблиці 3 представлено В таблиці 4 дано алгоритм формування результату порівняння двох чисел А і В у КЛ для випадку коли nA nB . В таблиці 5 дано алгоритм функціонування суматора 17 за модулем два. 3 UA 92069 U На кресленні (лист 1, 2) представлена блок-схема корисної моделі, де 1, 2 - перший та другий інформаційні входи пристрою; 3, 4 - перший та другий вхідні регістри, які складаються з n підрегістрів для зберігання лишків у двійковому коді відповідно першого A a1,a2 ,..., an та 5 другого B b1, b2 ,..., bn чисел, що порівнюються, за відповідними модулями mi , i 1, n КЛ; 5, 6 перший і другий суматори, що реалізують відповідно операції 1 2 A 1 A KHA a1,a ,..., a a1, a2,..., a 0,a1,..., an , де ai1 a a modmi , та m n n i i 2 B b ,b ,..., b b , b ,..., b 0,b1,..., b1 ; 7, 8 - перший і другий блоки B B KH m1 1 2 n 1 2 n 2 n зберігання констант нулевізації (БКН); 90 9N1 , 10 0 10N1 - перша та друга групи суматорів, m що реалізують операції відповідно A 1 0 z 0 , A 1 m1 z1,..., A 1 N 1 m1 zN1 та m m n 10 B 1 0 z , B m1 z1,..., B N 1 m1 zN1 (де N m i ; наприклад для КЛ, що m 0 m1 m1 i 2 задано модулями m1 2 , m2 3 , m3 5 , N 3 5 15 ); 110 11N1 - шини подачі числових значень констант виду 0, m1, 2 m1,..., N 1 m1 представлених у КЛ; 12 - схема порівняння однорядкового 15 20 25 30 коду n KN A zN1, zN2,..., z0 виду та n KN B zN1, zN 2,..., z , 0 де n A nB 0, N 1 - номер позиції нуля в запису однорядкового коду (рахується справа наліво); 13, 14 - перший і другий елементи І; 15, 16 - перший і другий елементи АБО; 17 - суматор за модулем два; 18, 19 і 20 - перший, другий і третій елементи заборони (ЕЗ); 21 - третій елемент І; 22, 23, 24 і 25 - перша, друга, третя і четверта групи елементів І; 261, 262 - перша та друга шини подачі додатної ознаки; 271, 272 - перша та друга шини подачі від'ємної ознаки; 28 - третій M суматор, що реалізує операцію виду A A ; 29 - четвертий суматор, що реалізує операцію 2 M виду A A ; 30 - перша група елементів АБО; 31 - перший прийомний регістр; 32 - п'ятий 2 M суматор, що реалізує операцію виду B B ; 33 - шостий суматор, що реалізує операцію 2 M виду B B ; 34 - друга група елементів АБО; 35 - другий прийомний регістр; 36 - шина 2 M подачі значення ; 37, 38 і 39 - перший A B , другий A B і третій A B виходи 2 пристрою. Перший 1 і другий 2 входи пристрою підключено до входів відповідно першого 3 та другого 4 вхідних регістрів, до перших входів першого 5 та другого 6 суматорів підключено виходи відповідно першого 7 та другого 8 блоків констант нулевізації, виходи першого 5 та другого 6 суматорів підключено до перших входів відповідно суматорів першої 90 9N1 та другої 10 0 10N1 , груп, до других входів суматорів першої 90 9N1 та другої 10 0 10N1 , груп підключені відповідні шини 110 11N1 подачі числових значень констант виду 0, m1, 2 m1,..., N 1 m1 ( N n m i ; , де m i - модулі КЛ; i 1 n ; n - кількість модулів КЛ; i2 35 40 mi mi 1 ), а виходи суматорів першої 90 9N1 та другої 10 0 10N1 груп підключено відповідно до перших і других груп входів схеми 12 порівняння однорядкового коду (СПОК), виходи першого 13 та другого 14 елементів І підключено до перших входів відповідно першого 15 та другого 16 елементів АБО, вихід суматора 17 за модулем два підключено до першого (забороненого) входу першого 18 елемента заборони, виходи першого 15 та другого 16 елементів АБО підключено до перших (інформаційних) входів відповідно другого 19 та третього 20 елементів заборони, вихід третього 21 елемента І підключено до других (заборонених) входів відповідно другого 19 та третього 20 елементів заборони, вихід першого 3 вхідного регістра підключено до перших входів елементів І першої 22 та другої 23 груп, а вихід другого 4 вхідного регістра підключено до перших входів елементів І третьої 24 та четвертої 25 груп, перша 26 1 шина додатної ознаки підключена до других входів елементів І першої 22 групи, а друга 26 2 шина додатної ознаки підключена до других входів елементів І третьої 24 групи, перша 27 1 шина від'ємної ознаки підключена до других входів елементів І другої 23 групи, а друга 27 2 шина 4 UA 92069 U 5 10 від'ємної ознаки підключена до других входів елементів І четвертої 25 групи, виходи елементів І першої 22 та другої 23 груп підключено до перших входів відповідно третього 28 та четвертого 29 суматорів, виходи яких через елементи АБО першої 30 групи підключено до входу першого 31 прийомного регістра, а виходи елементів І третьої 24 та четвертої 25 груп підключено до перших входів відповідно п'ятого 32 та шостого 33 суматорів, виходи яких через елементи АБО другої 34 групи підключено до входу другого 35 прийомного регістра, виходи першого 31 та другого 35 прийомних регістрів підключено до других входів відповідно першого 5 та другого 6 суматорів, вихід підрегістра лишку a1 за найменшим модулем m1 КЛ першого 31 прийомного регістра одночасно підключено до входу першого 7 блока констант нулевізації, до першого входу першого 13 елемента І, до першого входу третього 21 елемента І, а також підключено до першого входу суматора 17 за модулем два, а вихід підрегістра лишку b1 за найменшим модулем m1 КЛ другого 35 прийомного регістра одночасно підключено до входу другого 8 блока констант нулевізації, до першого входу другого 14 елемента І, до другого входу третього 21 елемента І, а також підключено до другого входу суматора 17 за модулем два, шина 36 подачі n M m i підключена до других входів третього 28, четвертого29, п'ятого 32 та i 1 шостого 33 суматорів, перший nA nB вихід СПОК підключено до других входів першого 13 та другого 14 елементів І, також до другого (інформаційного) входу першого 18 елемента заборони, вихід 37 якого є першим A B виходом пристрою, другий nA nB вихід СПОК M 2 15 значення 20 підключено до другого входу першого 15 елемента АБО, третій nA nB вихід СПОК підключено до другого входу другого 16 елемента АБО, виходи другого та третього елементів заборони є відповідно другим 38 A B і третім 39 A B виходами пристрою. Процес функціонування корисної моделі для порівняння двох чисел A a1,a2 ,..., an і B b1, b2 ,..., bn у КЛ зручно представити у наступному вигляді. 25 30 Через перший 1 та другий 2 входи пристрою перше A a1,a2 ,..., an та друге B b1, b2 ,..., bn числа (числа А та В представлені в КЛ сукупністю лишків, що представлені у двійковому коді), що порівнюються, надходять відповідно до першого 3 та другого 4 вхідних регістрів. У відповідності з формулами (2) елементи 22, 23, 28, 29, 30 та 24, 25, 32, 33, 34 формують ШФ A і B відповідно чисел А і В. Далі процес функціонування даного пристрою відповідає алгоритму роботи пристрою-прототипу для A і B . За значеннями a1 і b1 у відповідних БКН 7 і 8 вибираються значення a1, a 2 ,..., a і n 2 b1, b ,..., b . n Суматори 5 та 6 здійснюють операції відповідно та b ,b ,..., b b , b ,..., b 0,b ,..., b . На перші входи суматорів першої 1 2 A 1 A KHA a1,a ,..., a a1, a2,..., a 0,a1,..., an m n n 2 B 1 B KHB m 1 2 n 1 2 1 2 n 1 n 90 9N1 , групи надходять значення A m 1 , а на перші входи суматорів другої 10 0 10N1 групи 35 надходять значення B m 1 . На другі виходи суматорів першої 90 9N1 та другої 10 0 10N1 груп по шинах 11 надходять значення констант виду 0, m1, 2 m1, 3 m1,..., N 2 m1 , де N n mk . k 2 Вихідні сигнали суматорів першої 90 9N1 групи утворюють однорядковий код (ОК) виду n KN A zN1, zN 2,..., z2, z1, z0 . При цьому zn A 0 , якщо A m1 n A m1 0 та zn A 1 , якщо A m1 n A m1 0 . Вихідні сигнали суматорів другої 10 0 10N1 групи утворюють ОК виду 40 n KN B zN1, zN 2,..., z , z1, z . При цьому z n B 0 , якщо Bm1 nB m1 0 та znB 1, якщо 2 0 Bm1 nB m1 0 . Таким чином вихідні сигнали суматорів першої 90 9N1 (другої 10 0 10N1 ) груп для КЛ, що задано модулями m1 2 , m2 3 , m3 5 , створюють ОК виду n n 111 n n KN A zN1, zN2,..., z0 K15A ...0...111 ( KN B zN1, zN2,..., z K15B ...0...111 ), 111 0 де n A nB 0, N 1 - ознака позиції знаходження нуля в запису ОК, яка чисельно дорівнює 5 UA 92069 U n номеру (рахується з права наліво) позиції нуля в ОК K15A 5 10 15 20 K . Таким чином на перші та другі nB 15 n n групи входів схеми 12 порівняння ОК надходить значення відповідно ОК K15A і K15B . У відповідності з алгоритмом (1) розглянемо три можливих варіанту функціонування пристрою. Варіант 1. У випадку коли nA nB , пристрій функціонує наступним чином (табл. 4). Сигнал першої nA nB вихідної шини схеми 12 надходить до перших входів елементів І 13 і 14, а також надходить до першого (інформаційного) входу першого елемента 18 заборони. Елемент 18 заборони відкрито, якщо відсутній вихідний сигнал заборони суматора 17 за модулем два (коли a1 b1 0mod 2 ), тобто у випадку якщо a1 b1 0 , або a1 b1 1. В цьому випадку сигнал першої вихідної шини схеми 12 через відкритий елемент 18 заборони надходить до першого 37 виходу A B пристрою. В останніх випадках ( a1 1 , b1 0 та a1 0 , b1 1 ) перший елемент 18 заборони закрито, так як присутній вихідний сигнал суматора 17 за модулем два a1 b1 1mod 2 . Елементи 19 і 20 заборони відкриті у випадку коли відсутній вихідний сигнал (сигнал заборони) третього 21 елемента І ( a1 b1 0 , a1 1, b1 0 та a1 0 , b1 1 ), і елементи 19 і 20 заборони закриті у випадку коли присутній сигнал заборони третього 21 елемента І a1 b1 1 . Якщо a1 1 і b1 0 , тоді відкрито перший 13 елемент І, вихідний сигнал якого через перший 15 елемент АБО, через відкритий другий 19 елемент заборони надходить до другого 38 виходу A B пристрою. Якщо a1 0 і b1 1 , тоді відкрито другий 14 елемент І, вихідний сигнал якого через другий 16 елемент АБО, через відкритий третій 20 елемент заборони надходить до третього 39 виходу A B пристрою. Варіант 2. У випадку коли n n , сигнал другої nA nB вихідної шини схеми 12 через A B перший 15 елемент АБО, через відкритий (відсутній вихідний сигнал заборони третього 21 елемента І) другий 19 елемент заборони надходить до другого 38 виходу A B пристрою. 25 Варіант 3. У випадку коли nA nB , сигнал третьої nA nB вихідної шини схеми 12 через другий 16 елемент АБО, через відкритий (відсутній вихідний сигнал заборони третього 21 елемента І) третій 20 елемент заборони надходить до третього 39 виходу A B пристрою. Розглянемо конкретні числові приклади порівняння чисел КЛ, який заданий модулями m1 2 , m2 3 , m3 5 (креслення (лист 1, 2), таблиці 1-6). 6 UA 92069 U Таблиця 1 Об'єм кодових слів у КЛ A B у ПСЧ A B у ПСЧ -15 -14 -13 -12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 A B у КЛ m1 2 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 m2 3 00 01 10 00 01 10 00 01 10 00 01 10 00 01 10 00 01 10 00 01 10 00 01 10 00 01 10 00 01 10 m3 5 000 001 010 011 100 000 001 010 011 100 000 001 010 011 100 000 001 010 011 100 000 001 010 011 100 000 001 010 011 100 Таблиця 2 Константи нулевізації для m1 2 (A) а1 (b1) 0 1 (B) Константи KH (KH ) у КЛ m2 3 00 01 m1 2 0 1 7 m3 5 000 001 UA 92069 U Таблиця 3 n Константи для груп суматорів 90 9N1 і 10 0 10N1 та значення однорядкового коду K15A K nB 15 для КЛ ( m1 2 ) Значення n K A , n A nB 0,14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Значення j m1 j 0,14 шин 11 УКЛ У ПСЧ m3 5 m1 2 m2 3 0 0 00 000 2 0 10 010 4 0 01 100 6 0 00 001 8 0 10 011 10 0 01 000 12 0 00 010 14 0 10 100 16 0 01 001 18 0 00 011 20 0 10 000 22 0 01 010 24 0 00 100 26 0 10 001 28 0 01 011 n K B 15 {111111111111110} {111111111111101} {111111111111011} {111111111110111} {111111111101111} {111111111011111} {111111110111111} {111111101111111} {111111011111111} {111110111111111} {111101111111111} {111011111111111} {110111111111111} {101111111111111} {011111111111111} Таблиця 4 Алгоритм формування результату порівняння двох чисел A і B у КЛ для випадку коли nA nB Перший nA nB вихід СПОК 12 Послідовність елементів, що проходить сигнал від першого Виходи пристрою nA nB виходу СПОК 12 до виходів пристрою 12-18-37 Перший A B 37 12-14-16-20-39 Третій A B 39 a1 b1 0 0 0 1 1 0 12-13-15-19-38 1 1 12-18-37 Другий A B 38 Перший A B 37 Таблиця 5 Алгоритм функціонування суматора 17 за модулем два Входи суматора 17 за модулем два a1 b1 0 0 0 1 1 0 1 1 5 Вихід суматора 17 за модулем два 0 1 1 0 Приклад 1. Нехай A 3 і B 4 . У цьому випадку присутні сигнали шин 26 1 і 272, що відкривають елементи І відповідно першої 22 і четвертої 25 груп. З виходу регістра 3 значення A 1 00, 011 у КЛ через відкрити елементи І 22 надходить до перших входів третього суматора , , 28. З виходу регістра 4 значення B 0, 01 100 у КЛ через відкриті елементи І 25 надходить до 8 UA 92069 U перших входів шостого 33 суматора. По шині 36 до других входів суматорів 28 і 33 надходить M 15 1, 00, 000 . З виходів суматорів 28 і 33 відповідні значення значення 2 A 5 M A 1, 00, 000 1, 00, 011 0, 00, 011 2 і B M B 1, 00, 000 0, 01,100 1,10, 001 2 через відповідні елементи АБО першої 30 і другої 34 груп надходять на входи відповідно першого 31 і другого 35 прийомних регістрів. У подальшому порівняння двох чисел A 0, 00, 011 і B 1 10, 001 здійснюється у відповідності до алгоритму (1). За значенням a1 0 числа , A 0, 00, 011 у БКН 7 (табл. 2) вибираємо константу KH A 0, 00, 000 . Суматор 5 реалізує A 0, 00, 011 0, 00, 000 0, 00, 011 . За значенням b 1 числа операцію виду A 1 A KH 1 m B 1 10, 001 , 10 у БКН 8 вибираємо KH B 1, 01, 001 . Суматор 6 реалізує операцію , , B KHB 1 10, 001 1 01 001 0, 01 000 . Значення A 1 і B 1 надходять на перші , , m m Bm1 входи відповідних суматорів першої 9 і другої 10 груп. На другі входи цих суматорів по шинам 11 0,1 m1, 2 m1,...,13 m1,14 m1 надходять чисельні значення у КЛ. Так, як A 1 n A m1 18 9 2 0 , тоді з виходів суматорів 90 914 сформований ОК m 9 надходить до перших входів СПОК 12. Так, як K 1111101111 11111 15 15 20 5 B 1 nB m1 10 5 2 0 , тоді виходів суматорів 100 1014 ОК K15 1111111110 11111 m надходить до других входів СПОК 12. Таким чином, якщо n A 9 nB 5 , тоді на другому nA nB виході СПОК 12 присутній сигнал, який через елемент АБО 15, відкритий (відсутній вихідний сигнал елемента 21, так, як a1 b1 0 1 1mod 2 ) EЗ 19 надходить до виходу 38 B . У відповідності зі співвідношенням (3) маємо, що A B . A Перевірка: A 3 B 4 . Приклад 2. Нехай A 2 і B 3 . У цьому випадку присутні сигнали шин 271 і 272, що відкривають елементи І відповідно другої 23 і четвертої 25 груп. З виходу регістра 3 значення A 0,10, 010 через елементи І 23 надходить до перших входів суматора 29, з виходу якого M A 1, 00, 000 0,10, 010 1 01, 011 через елементи АБО 30 надходить до , 2 , входу регістра 31. З виходу регістра 4 значення B 1 00, 011 через елементи І 25 надходить до перших входів суматора 33, з виходу якого значення M B B 1, 00, 000 1, 00, 011 0, 00, 010 через елементи АБО 34 надходить до входу 2 , , регістра 35. За значенням a1 1 числа A 1 01 011 у БКН 7 вибираємо константу значення A 25 KH A 1, 01, 001 . 30 Суматор 5 реалізує операцію , , A 1 A KHA 1 01 011 1 01 001 0, 00, 010 . За значенням b1 0 числа B 0, 00, 010 у , , m KH B 0, 00, 000 . БКН 8 вибираємо Суматор 6 реалізує операцію B 0, 00, 010 0, 00, 000 0, 00, 010 . Значення A і B надходять на перші B B KH m1 m1 m1 A n A m1 12 6 2 0 входи відповідних суматорів першої 9 і другої 10 груп. Так, як m1 , і B 1 nB m1 12 6 2 0 m , тоді маємо, що для A і B ОК має однакове значення 35 6 K15 1111111101 11111 . Тобто маємо, що n A nB 6 . Присутній вихідний сигнал першого nA nB виходу СПОК 12. Тоді у відповідності з табл. 4 присутній сигнал шини 38 A B . У відповідності з співвідношенням (3) маємо, що A B . Перевірка: A 2 B 3 . Таким чином, запропонована корисна модель для порівняння двох чисел A a1,a2 ,..., an і 40 B b1, b2 ,..., bn , що представлені у КЛ, дозволяє забезпечити розширення функціональних можливостей пристрою-прототипу. Це досягається за рахунок забезпечення запропонованим 9 UA 92069 U 5 пристроєм, крім виконання їм операції арифметичного порівняння, додатково виконання також і операції алгебраїчного порівняння двох чисел КЛ. Розширення функціональних можливостей пристрою-прототипу досягається за рахунок використання модернізованого алгоритму порівняння двох чисел КЛ шляхом представлення вихідних чисел А і В у ШФ. Даний ефект досягається при збереженні усіх функціональних і технічних властивостей пристрою-прототипу. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 10 15 Пристрій для арифметичного та алгебраїчного порівняння двох чисел класу лишків (КЛ), що містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший, другий і третій елементи І, перший і другий елементи АБО, перший, другий та третій елементи заборони, суматор за модулем два, при цьому перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, до перших входів першого та другого суматорів підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені відповідні шини подачі констант виду 0, m1, 2 m1,...,N 1 m1 ( N n m i ; де m i - модулі КЛ; n - кількість модулів КЛ; i 2 20 25 30 35 40 45 50 mi mi1 ), а виходи суматорів першої та другої груп підключено відповідно до перших і других груп входів схеми порівняння однорядкового коду (СПОК), виходи першого та другого елементів І підключено до перших входів відповідно першого та другого елементів АБО, вихід суматора за модулем два підключено до першого (забороненого) входу першого елемента заборони, виходи першого та другого елементів АБО підключено до перших (інформаційних) входів відповідно другого та третього елементів заборони, вихід третього елемента І підключено до других (заборонених) входів відповідно другого та третього елементів заборони, який відрізняється тим, що введено третій, четвертий, п'ятий і шостий суматори, першу, другу, третю і четверту групи елементів І, першу і другу групи елементів АБО, перший і другий прийомні регістри, при цьому вихід першого вхідного регістра підключено до перших входів елементів І першої та другої груп, а вихід другого вхідного регістра підключено до перших входів елементів І третьої та четвертої груп, перша шина додатної ознаки підключена до других входів елементів І першої групи, а друга шина додатної ознаки підключена до других входів елементів І третьої групи, перша шина від'ємної ознаки підключена до других входів елементів І другої групи, а друга шина від'ємної ознаки підключена до других входів елементів І четвертої групи, виходи елементів І першої та другої груп підключено до перших входів відповідно третього та четвертого суматорів, виходи яких через елементи АБО першої групи підключено до входу першого прийомного регістра, а виходи елементів І третьої та четвертої груп підключено до перших входів відповідно п'ятого та шостого суматорів, виходи яких через елементи АБО другої групи підключено до входу другого прийомного регістра, виходи першого та другого прийомних регістрів підключено до других входів відповідно першого та другого суматорів, вихід підрегістра лишку a1 за найменшим модулем m1 КЛ першого прийомного регістра одночасно підключено до входу першого блока констант нулевізації, до першого входу першого елемента І, до першого входу третього елемента І, а також підключено до першого входу суматора за модулем два, а вихід підрегістра лишку b1 за найменшим модулем m1 КЛ другого прийомного регістра одночасно підключено до входу другого блока констант нулевізації, до першого входу другого елемента І, до другого входу третього елемента І, а також підключено до другого входу n суматора за модулем два, шина подачі значення M / 2 M m i підключена до других входів i 1 третього, четвертого, п'ятого та шостого суматорів, перший nA nB вихід СПОК підключено до других входів першого та другого елементів І, також до другого (інформаційного) входу першого елемента заборони, вихід якого є першим A B виходом пристрою, другий nA nB вихід СПОК підключено до другого входу першого елемента АБО, третій nA nB вихід СПОК підключено до другого входу другого елемента АБО, виходи другого та третього елементів заборони є відповідно другим A B і третім A B виходами пристрою. 10 UA 92069 U Комп’ютерна верстка С. Чулій Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 11
ДивитисяДодаткова інформація
МПК / Мітки
МПК: G06F 7/04
Мітки: пристрій, алгебраїчного, чисел, порівняння, арифметичного, класу, двох, лишків
Код посилання
<a href="https://ua.patents.su/13-92069-pristrijj-dlya-arifmetichnogo-ta-algebrachnogo-porivnyannya-dvokh-chisel-klasu-lishkiv.html" target="_blank" rel="follow" title="База патентів України">Пристрій для арифметичного та алгебраїчного порівняння двох чисел класу лишків</a>
Попередній патент: Спосіб керування роботою тиристорного електроприводу постійного струму при аномальних явищах в напрузі живильної мережі
Наступний патент: Комбінований турбопривід насоса для аварійної подачі водних середовищ
Випадковий патент: Спосіб експрес-оцінки метрологічних характеристик вузла обліку газу середнього або високого тиску за місцем експлуатації