Пристрій для арифметичного порівняння чисел у класі лишків

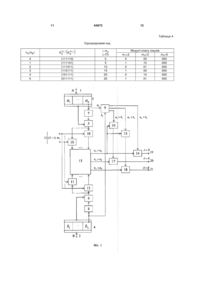
Пристрій для арифметичного порівняння чисел у класі лишків, що містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, при цьому, перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого блоків констант нулевізації, до входів яких підключено виходи підрегістрів за найбільшим модулем КЛ mn відповідних вхідних регістрів, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені відповідні шини подачі констант виду (19) 1 3 64973 Найбільш близьким за технічною суттю до запропонованої корисної моделі є пристрій (а.с. СССР № 1037244, опубл. БВ № 31, 1983 р., G 06 F 7/04), де реалізується операція порівняння двох чисел у КЛ. Пристрій для порівняння чисел у класу лишків містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації (БКН), перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду (СПОК), причому, перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп до других входів яких підключені шини подачі констант, виходи суматорів першої та другої груп підключено до перших і других входів СПОК. Недолік прототипу - низька точність порівняння двох чисел. Недолік обумовлений тим, що числа A  (1, 2,...,n ) і B  (b1, b2,...,bn ) , що представлені у КЛ, порівнюються тільки з точністю до довжини інтервалу (де ( j  mn, ( j  1)  mn ) , n j  0, N  1,N  П mk ) k 1 k 1 знаходження чисел A  (1, 2,...,n ) і B  (b1, b2,...,bn ) , що порівнюються. Технічною задачею запропонованої корисної моделі є підвищення точності арифметичного порівняння чисел і A  (1, 2,...,n ) B  (b1, b2,...,bn ) . Поставлена задача вирішується наступним чином. У пристрій для арифметичного порівняння чисел у класі лишків, що містить перший і другий вхідні регістри, перший і другий БКН, перший і другий суматори, першу і другу групи суматорів, СПОК, при цьому, перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого БКН, до входів яких підключено виходи підрегістрів за найбільшим модулем КЛ mn відповідних вхідних регістрів, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені відповідні шини подачі констант виду 0, mn,2  mn,...,(N  1)  mn n 1 (N  П mi; mi (i  1, n) i1 модулі КЛ; n- кількість модулів КЛ; mi  mi1 ), а виходи суматорів першої та другої груп підключено відповідно до перших і других груп входів СПОК, введено, схему порівняння лишків  n і b n за модулем mn КЛ, перший, другий та третій елементи I, перший та другий елементи АБО, при цьому ви 4 ходи підрегістрів за найбільшим модулем КЛ mn першого та другого вхідних регістрів підключені до входів схеми порівняння лишків  n і b n за модулем mn КЛ, перший (nA  nB ) вихід СПОК підключено до перших входів першого, другого та третього елементів І, до других входів яких підключені відповідно виходи рівно (n  bn ) , менше (n  bin ) і більше (n  bn ) схеми порівняння лишків 3  n bn за модулем mn КЛ, а другий (nA  nB ) вихід СПОК підключено до першого входу першого елемента АБО, до другого входу якого підключено вихід третього елемента І, а третій (nA  nB ) вихід схеми порівняння однорядкового коду підключено до першого входу другого елемента АБО, до другого входу якого підключено вихід другого елемента І, вихід першого елемента І, вихід першого елемента АБО і вихід другого елемента АБО є відповідно першим (A  B) , другим (A  B) і третім (A  B) виходами пристрою. В цьому випадку введення вказаних ознак дозволяє підвищити точність арифметичного порівняння двох чисел і A  (1, 2,...,n ) B  (b1, b2,...,bn ) , що представлені у КЛ, з точністю до довжини ( j  mn,( j  1)  mn ) , інтервалу n j  0, N  1,N  П mk ) k 1 k 1 знаходження (де чисел A  (1, 2,...,n ) і B  (b1, b2,...,bn ) , що порівнюються. На кресленні (фіг. 1) представлена блок-схема корисної моделі. В таблиці 1 представлена таблиця кодових слів КЛ. В таблиці 2 представлені вміст блоків констант нулевізації (БКН) 5 і 6 (див. фіг. 1). В таблиці 3 представлені набори констант у КЛ за основами m1  2, m2  3 і m3  5 . В таблиці 4 представлений вид однорядкового коду для mn  m3  5 . На кресленні (фіг. 1) представлена блок-схема корисної моделі, де 1, 2 - перший та другий інформаційні входи пристрою; 3, 4 - перший та другий вхідні регістри, які складаються з n підрегістрів для зберігання лишків відповідно першого A  (1, 2,...,n ) та другого B  (b1, b2,...,bn ) чисел, що порівнюються, за відповідними модулями {m}, i  1 n КЛ; 5, 6 - перший і другий суматори, що , реалізують відповідно операції ' ( Amn  A  KH( A )  (1, 2,...,n )  (1, '2,...n )  (11), (1),...,(1)1,0) 2 n m n та; ' ( Bmn  B  KH(B)  (b1, b2,...,bn )  (b1, b'2,...,bn )  (b11), b(1),...,b(1)1,0) 2 n m n , 7, 8 - перший і другий блоки зберігання констант ' ' нулевізації (КН) виду KH( A )  (1, '2,...,n1, n ) і m n KH(B) mn ' '  (b1, b'2,...,bn1, bn ) ; 9 - схема порівняння ли 5 64973 шків  n і b n за модулем mn КЛ; 10, 11 - перша та друга групи суматорів, що реалізують в загальному випадку операції відповідно Amn  0  z0 , n 1 Amn  mn  z1,..., Amn  (N  1)  mn  zN1 (N  П mi ) , i1 Bmn  0  z'0 , та ' Bmn  mn  z'0 ,...,Bmn  (N  1)  mn  zN1 однорядковий код утворюючі (ОК) виду (n (n ' KN A )  {zN1, zN2,..., z0 } та KN B )  {z'N1 , zN2,..., z'0 } , де nA (nB )  0, N  1 - номер позиції нуля в запису однорядкового коду (Для прикладу. Нехай КЛ заданий модулями m1  2 , m2  3 , m3  5 , при цьому N  2  3  6 . В цьому випадку однорядковий код має вигляд K (n A )  {z5 , z 4 ,..., z0 } 6 та K (nB )  {z'5 , z'4 ,..., z'0 } , де nA (nB )  0,5 - номер пози6 ції нуля в запису однорядкового коду); 12 - шини подачі значень констант виду 0, mn,2 mn,...,(N  1)  mn представлених у КЛ; 13 схема порівняння однорядкового коду виду 6 входу першого 17 елемента АБО, до другого входу якого підключено вихід третього 16 елемента І, а третій (nA  nB ) вихід схеми 13 порівняння однорядкового коду підключено до першого входу другого 18 елемента АБО, до другого входу якого підключено вихід другого 15 елемента І. Вихід першого 14 елемента І, вихід першого 17 елемента АБО і вихід другого 18 елемента АБО є відповідно першим 19 (A  B) , другим 20 (A  B) і третім 21 (A  B) виходами пристрою. Представимо процес функціонування корисної моделі для арифметичного порівняння двох чисел A  (1, 2,...,n ) і B  (b1, b2,...,bn ) у КЛ. Через перший 1 та другий 2 входи пристрою перше A  (1, 2,...,n ) та друге B  (b1, b2,...,bn ) числа (числа А та В представлені в КЛ сукупністю , {mi } лишків, i  1 n , що представлені у двійковому коді), що порівнюються, надходять відповідно до першого 3 та другого 4 вхідних регістрів. За значеннями  n і b n у відповідних БКН 7 і 8 вибираються значення констант ' ' KH( A )  (1, '2,...,n1, n ) m і n (n (n ' KN A )  {zN1, zN2,..., z0 } та KN B )  {z'N1 , zN2,..., z'0 } ; ' ' KH(B)  (b1, b'2,...,bn1, bn ) нулевізації чисел А і В. m 14, 15 і 16 - перший, другий і третій елементи І; 17, 18 - перший і другий елементи АБО; 19, 20 і 21 перший (A  B) , другий (A  B) і третій (A  B) виходи пристрою. Перший 1 і другий 2 входи пристрою підключено до входів відповідно першого 3 та другого 4 вхідних регістрів, виходи яких підключено до перших входів відповідно першого 5 та другого 6 суматорів, до других входів яких підключено виходи відповідно першого 7 та другого 8 блоків констант нулевізації, до входів яких і до входів схеми 9 порівняння лишків  n і b n за модулем mn КЛ, підключено виходи підрегістрів за найбільшим модулем КЛ mn відповідних вхідних регістрів 3 і 4. Виходи першого 5 та другого 6 суматорів підключено до перших входів відповідно суматорів першої 10 та другої 11 груп, до других входів яких підключені відповідні шини 12 подачі констант виду Одноразово з цим значення  n і b n надходять до входу схеми 9 порівняння. Суматори 5 та 6 здійснюють операції відповідно n ' ( Amn  A  KH( A )  (1, 2,...,n )  (1, '2,...n )  (11), (1),...,(1)1,0) 2 n m n та ' ( Bmn  B  KH(B)  (b1, b2,...,bn )  (b1, b'2,...bn )  (b11), b(1),...,b(1)1,0) 2 n m n . На перші входи суматорів першої 10 групи надходять значення A m n , а на перші входи суматорів другої 11 групи надходять значення Bmn . На другі виходи суматорів першої 10 та другої 11 груп по шинах 12 надходять відповідні значення 0, mn, 2  m,...,(N  1)  mn . Вихідні сигнали першої 10 групи суматорів (n ) утворюють ОК виду KN A  {zN1, zN2,..., z2, z1, z0 } , n 1 де i1 znA  0 , якщо Amn nA  mn  0 0, mn,2  mn,...,(N  1)  mn (N  П ; де m1 - модулі КЛ; n - кількість модулів КЛ; mi  mi1) . Виходи суматорів першої 10 та другої 11 груп підключені відповідно до перших і других груп входів схеми 13 порівняння однорядкового коду виду (n KN A )  {zN1, zN2,..., z0 } та (n KN B )  ' ' {z N1 , zN2,..., z'0 } . Перший (nA  nB ) вихід схеми 13 порівняння однорядкового коду підключено до перших входів першого 14, другого 15 та третього 16 елементів І, до других входів яких підключені відповідно виходи рівно (n  bn ) , менше (n  bn ) і більше (n  bn ) схеми 9 порівняння лишків за модулем mn КЛ. Другий (nA  nB ) вихід схеми 13 порівняння однорядкового коду підключено до першого zn A  0; zl  1 l  0, N  1 l  nA . , , При цьому та zn A  1 , якщо Amn  nA  mn  0 . Вихідні сигнали другої 11 групи суматорів утворюють ОК (n ' KN A )  {z'N1 , z'N2 ,..., z'2 , z1, z'0 } , виду де znB  0; zl  1 l  0, N  1 l  nB . При цьому znB  0 , , , Bmn  nB  mn  0 якщо та znB  1 , якщо Bmn  nB  mn  0 . Таким чином вихідні сигнали су маторів першої 10 та другої 11 груп створюють ОК (n KN A )  {zN1, zN2,..., z0 } виду (n KN B ) (n KN A )  ' ' {z N1 , zN2,..., z'0 } ,  {11111...0...111} та та тобто (n KN B )  {11111...0...111} , 7 64973 де nA (nB )  0, N  1 - ознака позиції знаходження нуля в запису ОК, яка чисельно дорівнює номеру (рахується зліва направо) позиції нуля в ОК. Таким чином на перші та другі групи входів схеми 13 порівняння надходить значення відповідно ОК (n KN A ) 8 ' повідає тому, що n  3  001  bn  b3  100 , відкриває другий 15 елемент І. Суматори 5 і 6 реалізують операції Amn  A 21  KH( A )  (1 00, 001)  (1 01 001)  (0,10, 000) , , , і і Bmn  B24  KH(B )  (0, 00,100)  (0, 01 100)  (0,10, 000) , Якщо nA  nB , тоді на першому виході СПОК 13 присутній вихідний сигнал, який надходить на перші входи першого 14, другого 15 і третього 16 елементів І, на другі входи яких надходять вихідні сигнали схеми порівняння 9, що означають відповідно рівно (n  bn ) , менше (n  bn ) і більше . Значення A m n надходить до перших входів су (n  bn ) та відкривають відповідні перший 14, другий 15 і третій 16 елементи І. Вихід елемента І 14 є першим (А=В) виходом пристрою. Якщо nA  nB , тоді на другому виході СПОК 13 присутній вихідний сигнал, що надходить до входу першого елемента 17 АБО, вихід якого є другим (A  B) виходом пристрою. ОК Якщо nA  nB , тоді на третьому виході СПОК 13 присутній вихідний сигнал, що надходить до входу другого елемента 18 АБО, вихід якого є третім (A  B) виходом пристрою. Розглянемо конкретний приклад порівняння чисел у КЛ, що заданий модулями m1  2 , m2  3 ' (n  3  001  bn  b3  100) елемент І 15, елемент АБО 18 надходить до виходу 21, що відповідає умові A  B . Перевірка: A21  (1 00, 001  B24  (0,00,100) . , ) Таким чином, запропонована корисна модель дозволяє підвищити точність арифметичного порівняння двох чисел і A  (1, 2,...,n ) (n KN B ) . і n3  5 (таблиця 1-4, фіг. 1). Для даного КЛ у таблиці 1 представлені кодові слова. У таблиці 2 представлено константи нулевізації (вміст відповідно БКН 7 і 8), а у таблиці 3 представлено набори констант у К Л за основами m1  2 , m2  3 і n3  5 , що надходять по шинах 12. Розглянемо приклад арифметичного порівняння двох чисел A21  (100,001 і B24  (0,00,100) , ) ' для даного КЛ. За значенням n  3  001 та bn  b3  100 (див. табл. 1) у БКН 7 і 8 вибираються КН (B) KH ' n (табл.  (1 01 001 . , , ) 2) виду KH( A )  (101001) , , Одночасно і значення  3  001 і bn  b3  100 надходять до входу схеми порівняння 9, з виходу якої сигнал, що від маторів першої 10 групи, а значення Bmn надходить до перших входів суматорів другої 11 групи. На другі входи суматорів 10 і 11 по шинах 12 надходять константи виду 0, 5, 10, 15, 20, 25 у КЛ (табл. 3). На виходах суматорів 10 і 11 формується виду K(nB )  K ( 4 )  {101111 } 6 6 K(n A )  K( 4 )  {101111 , } 6 6 (табл. 4), що надходить відповідно на перші і другі групи входів СПОК. Так, як пА=пв=4, тоді на одній з вихідних шин СПОК присутній сигнал, (що відповідає умові nA  nB ), який через відкритий B  (b1, b2,...,bn ) , що представлені у КЛ, з точністю до однієї одиниці довжини інтервалу ( j  mn, ( j  1)  mn ) , тобто забезпечується максимальна точність порівняння чисел А і В. Це досягається за рахунок застосування додаткової процедури порівняння лишків  n і b n за модулем mn , шляхом введення сукупності елементів I і АБО та схеми порівняння значень  n і b n . При цьому швидкість порівняння двох чисел А і В не зменшується, оскільки схема 9 порівняння лишків  n і b n та схема 13 порівняння однорядкового коду функціонують паралельно у часі. 9 64973 10 Таблиця 1 Таблиця кодових слів А(В) у ПСЧ m1=2 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 А(В) у КЛ m2=3 00 01 10 00 01 10 00 01 10 00 01 10 00 01 10 m3=5 000 001 010 011 100 000 001 010 011 100 000 001 010 011 100 А(В) у ПСЧ 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 m1=2 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 А(В) у КЛ m2=3 00 01 10 00 01 10 00 01 10 00 01 10 00 01 10 m3=5 000 001 010 011 100 000 001 010 011 100 000 001 010 011 100 Таблиця 2 Константи нулевізації а3 (b3) 000 001 010 011 100 m1=2 0 1 0 1 0 Константи КН (В) (КН ) у КЛ m2=3 00 01 10 00 01 (А) m3=5 000 001 010 011 100 Таблиця 3 Константи суматорів j  m3 ( j0,5 ) 0 5 10 15 20 25 M1=2 0 1 0 1 0 1 Константи у КЛ m2=3 00 10 01 00 10 01 m3=5 000 000 000 000 000 000 11 64973 12 Таблиця 4 Однорядковий код  nA (nB ) K(n A ) K(nB ) 6 6 0 1 2 3 4 5 {111110} {111101} {111011} {110111} {101111} {011111}  j  m3 ( j0,5 ) 0 5 10 15 20 25 m1=2 0 1 0 1 0 1 Модулі класу лишків m2=3 00 10 01 00 10 01 m3=5 000 000 000 000 000 000 13 Комп’ютерна верстка М. Мацело 64973 Підписне 14 Тираж 23 прим. Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601