Спосіб неруйнівного контролю та прогнозування довговічності деталей із деревини та деревних матеріалів під час їх циклічного навантаження

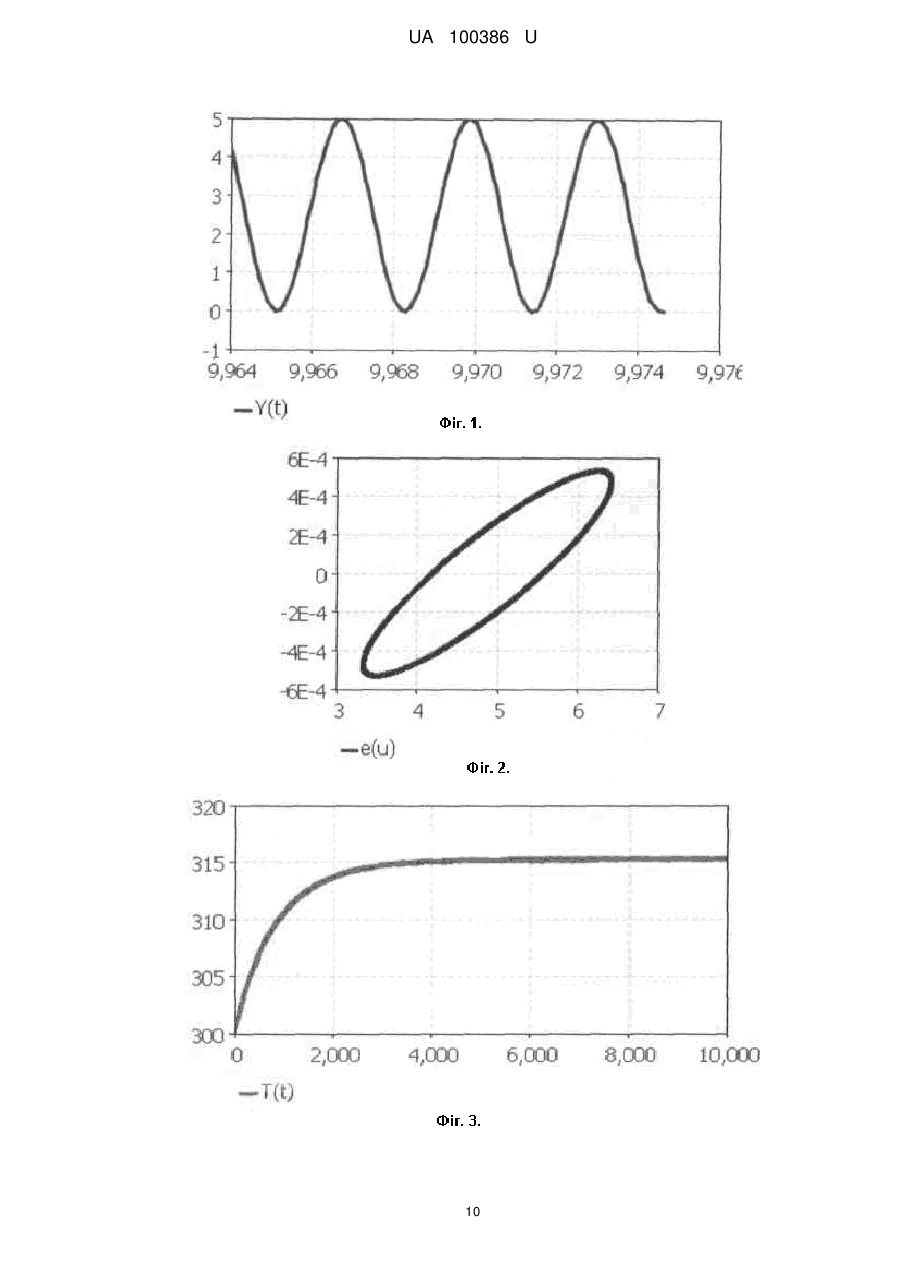
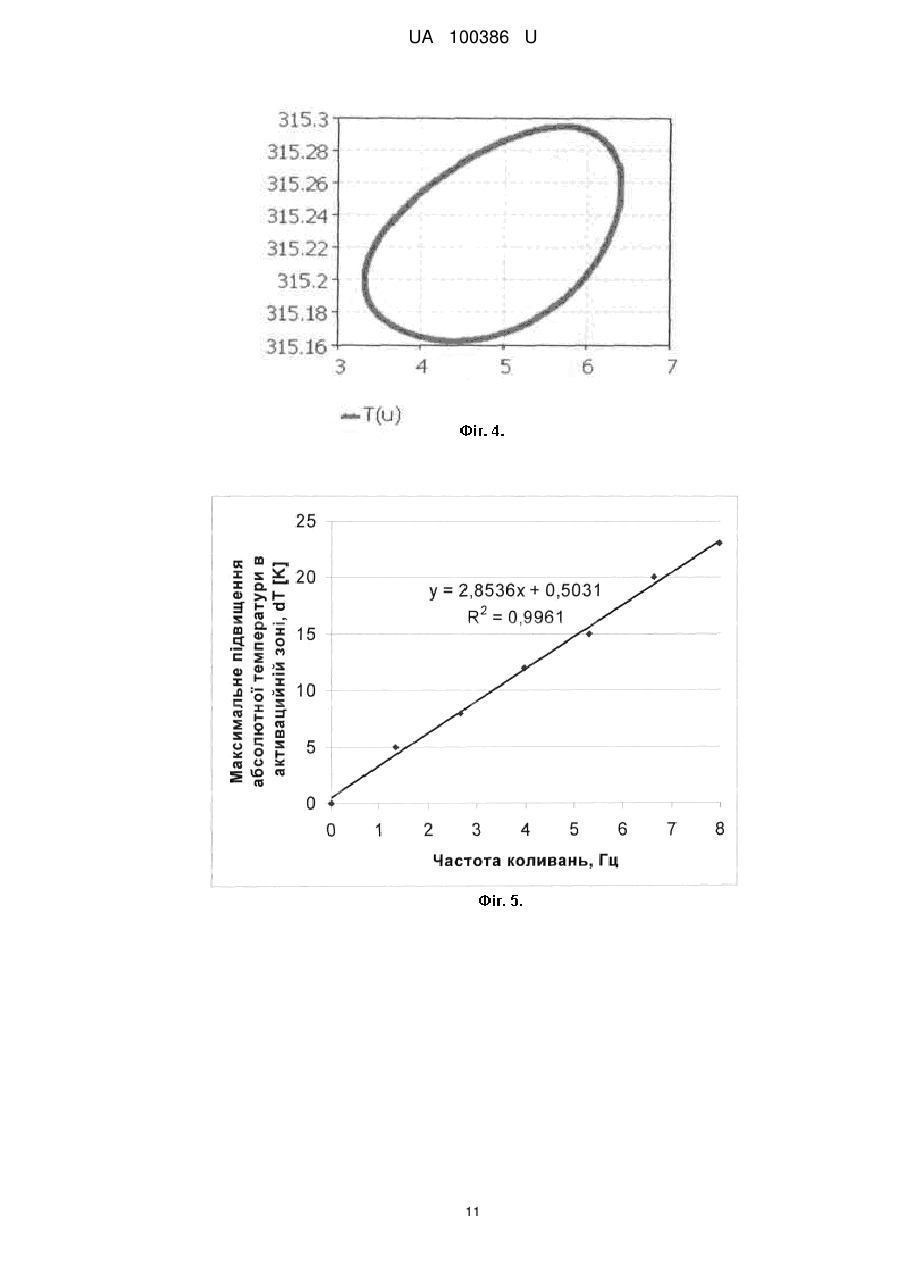
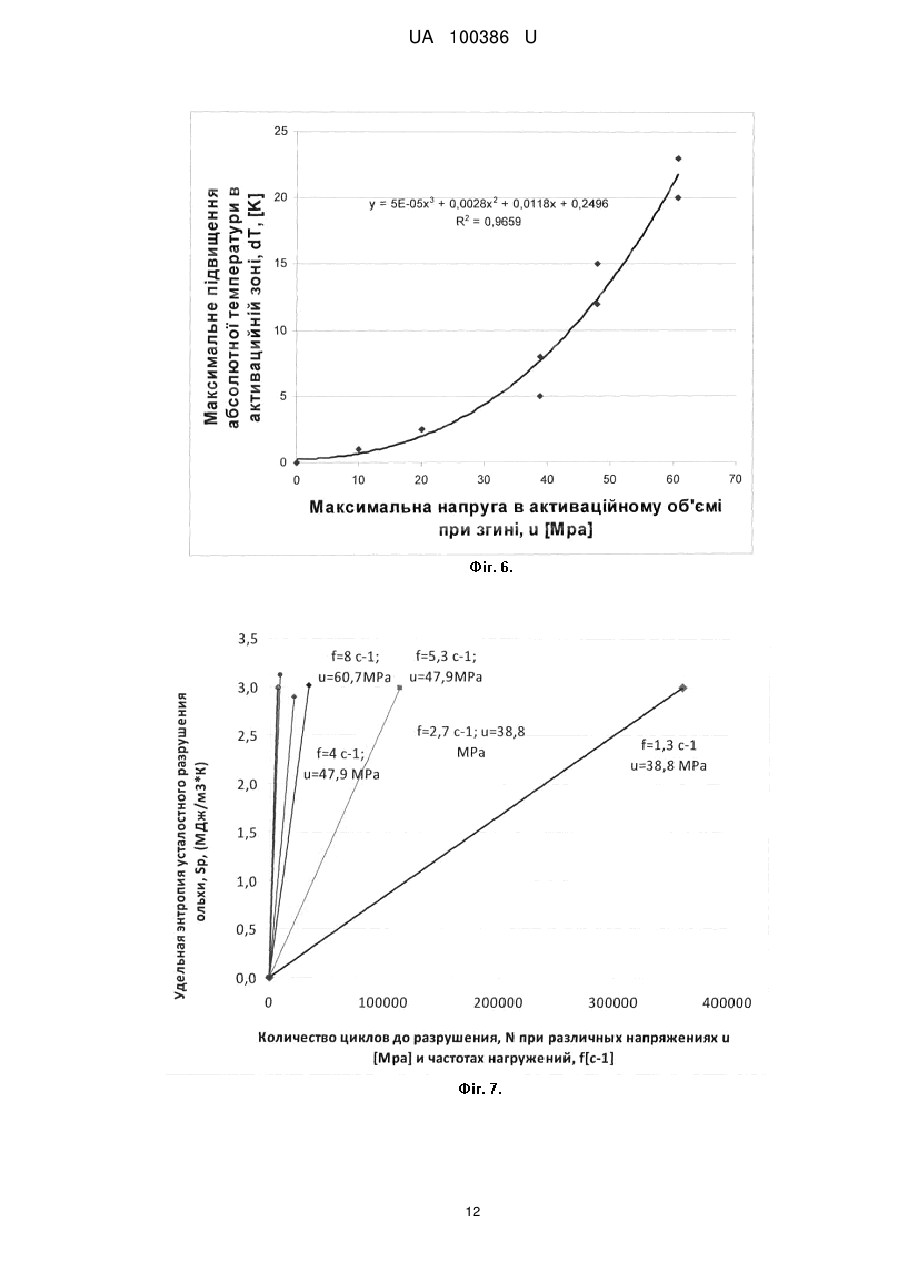
Реферат: Спосіб неруйнівного контролю та прогнозування довговічності деталей з деревини і деревних композиційних матеріалів при їх циклічному навантаженні включає порівняння ресурсу контрольованої деталі зі стовідсотковим ресурсом аналогічної деталі. Як запобіжне порівняння приймають величину питомої кількості виробленої ентропії в перебігу часу, що пройшов з моменту початку експлуатації деталі. Максимальне питоме виробництво ентропії для матеріалу, з якого виготовлена контрольована деталь, визначається експериментально, шляхом її циклічного навантаження при внутрішніх напруженнях і частотах навантаження, що перевищують частоти і навантаження, при яких відбувається експлуатація деталі. UA 100386 U (54) СПОСІБ НЕРУЙНІВНОГО КОНТРОЛЮ ТА ПРОГНОЗУВАННЯ ДОВГОВІЧНОСТІ ДЕТАЛЕЙ ІЗ ДЕРЕВИНИ ТА ДЕРЕВНИХ МАТЕРІАЛІВ ПІД ЧАС ЇХ ЦИКЛІЧНОГО НАВАНТАЖЕННЯ UA 100386 U UA 100386 U 5 10 15 20 25 30 Корисна модель належить до галузі дослідження фізико-механічних властивостей конструкцій, виготовлених із деревини та деревних композиційних матеріалів, та може бути використана як спосіб неруйнівного контролю, діагностики, прогнозування ресурсу деталей машин та конструкцій. Відомий спосіб визначення ресурсу машин та деталей машин, заснований на вимірюванні площі петлі гістерезису, що є мірою накопичення втомних пошкоджень під час циклічних навантажень. Оцінка ступеня втомних руйнувань складається при цьому у порівняні площі петлі гістерезису на початку прикладання циклічного навантаження та після роботи деталі [1]. Однак даний спосіб відрізняється великою трудомісткістю безпосереднього вимірювання площ петель гістерезису у процесі експлуатації деталей під час навантаження. Ресурс деталі може бути визначений залежністю площі петлі гістерезису від числа циклів навантаження, а площа петлі гістерезису визначається внутрішнім розсіюванням (дисипація) енергії у матеріалі деталі, що призводить до її нагрівання. Тому замість залежності площі петлі гістерезису можна використовувати залежність внутрішнього розсіювання енергії, яка у даному випадку пропорційна кількості виробленої ентропії залежно від числа циклів, цим самим прогнозувати ресурс деталі до моменту руйнування. Технічний результат полягає у скорочені часу випробувань, підвищенні достовірності результатів та якості вирішення завдань: неруйнівного контролю та діагностики деталей, прогнозування ресурсу, оцінки ступеня втомних пошкоджень під час повторно-змінному навантаженні. Поставлена задача вирішується тим, що у відомому способі неруйнівного контролю та прогнозування ресурсу (довговічності) деталей із деревини та деревних композиційних матеріалів під час їх циклічного навантаження, що включає порівняння ресурсу деталі, що контролюється, із стовідсотковим ресурсом аналогічної деталі, згідно з корисною моделлю, як запобіжне порівняння приймається величина кількості виробленої ентропії у проміжку часу, що пройшов з моменту початку експлуатації деталі, причому максимальне питоме виробництво ентропії для матеріалу, з якого виготовлена деталь, визначається експериментально, шляхом її циклічного навантаження при внутрішніх напруженнях та частотах навантаження, що перевищують напруження та частоти, при яких відбувається експлуатація деталі, при цьому величина загального запасу виробництва ентропії визначається за формулою: S   DN  f 2 2E  1 1    T  T N ,  o  (1) де S  - загальна питома кількість ентропії, що вироблена при циклічному навантаженні за весь час до руйнування,  Дж  ;  3  м    35 40 D f 2 2E  1 1  Дж    - дисипація енергії одиничного циклу навантаження,  ; T  T  м3     o   2 - питома робота при деформації за один цикл навантаження, в зоні максимальних 2E 3 внутрішніх напружень, і деформацій, max , max , Дж/м ; f - частота циклічного навантаження, (крім того вона визначає швидкість деформації і, отже, швидкість дисипації), Ошибка! Объект не может быть создан из кодов полей редактирования.; Τ - температура саморозігріву в активаційному обсязі, в зоні максимальних внутрішніх напружень при циклічному деформуванні із заданими параметрами (f, max ), К; Np  t p / f - число циклів до руйнування; 45 To - температура термостату, К; max - максимальні внутрішні напруження в активаційному обсязі, МПа; Ε - модуль пружності, МПа; причому ресурс вважається вичерпаним в разі досягнення числа циклів, що визначається за формулою: 1 UA 100386 U Ni   k S , (2) Di де k=0,5-0,6 - коефіцієнт запасу; Ni  - гранично допустима кількість циклів навантаження при заданих параметрах циклічного навантаження ( fi , i max , i max ), і при температурі саморозігріву, рівної Т і; 5 10 Di - дисипація енергії одиничного циклу навантаження при конкретних умовах експлуатації Di , ( fi , i max , Ti , To ). Процеси, що відбуваються при втомному деформуванні, є незворотними, та можуть бути пояснені на основі першого та другого законів термодинаміки стосовно до системи, властивості якої безперервні у просторі та часі. Відповідно до першого закону термодинаміки, загальна кількість енергії U у довільному контрольованому об'ємі може змінитися тільки, якщо енергія надходить у (або із) контрольованого об'єму через його границі: dU=dQ-dW, 15 де Q та W тепловий потік та робота через кордони контрольованого обсягу. З точки зору конкретної кількості теплового потоку та роботи, закон збереження енергії для контрольованого об'єму можна записати у вигляді:  20 25 (3) du  diJq  D  , dt (4) де ρ - щільність; u - питома внутрішня енергія; Jq - тепловий потік через границі об'єму; σ - симетричний тензор напруження; D  - симетричний тензор швидкостей деформації. Другий закон термодинаміки (нерівність Клаузіуса-Дюгема) постулює, що швидкість генерації ентропії завжди більша або дорівнює відношенню швидкості нагріву до температури Т:   Jq  ds  di  ,  T  dt   (5) де s - питома ентропія. Праву частину рівняння (5) можна записати у вигляді: 30   Jq  ds  di  .  T  dt   (6) Підставляючи рівняння (6) у рівняння (5) та замінюючи di Jq з рівняння (4) одержимо:  35 ds  du gradT    D    Jq  / T  0. dt  dt T  (7) Нехай ψ - питома вільна енергія та визначається як:   u  Ts . (8) Диференціюючи рівняння (8) за часом та розділивши результат на температуру Τ отримаємо: 40 2 UA 100386 U dT  ds 1 du .  d  s  /T  dt  dt T dt  dt (9) Комбінуючи рівняння (5 і 9) та нерівності (5 і 7) одержимо:  dT  gradT   d  B   /T  0. s   Jq  dt  T   dt   5 (10) При малих деформаціях, тензор швидкості деформації D можна замінити на загальну деформацію. Загальну деформацію надамо у вигляді суми пластичної та пружної деформації:   p   e . 10 (11) Термодинамічний потенціал у вигляді вільної питомої енергії  повинен бути вигнутий за температурою Τ та опуклим по інших змінних. Крім того, потенційна функція  залежить від зовнішніх та внутрішніх змінних:      , T, p ,  e , Vк , 15 (12) де Vк може бути будь-якої внутрішньої змінною. Посилаючись на рівняння (11) деформацію можна подати у вигляді   p   e , отже рівняння (12) має вигляд:      T,   p , Vк  T,  e , Vк  . (13) Швидкість питомої вільної енергії можна записати у вигляді: 20     t   e    T  V  e   .  T t V t  (14) Після підстановки рівняння (14) у рівняння (10), отримуємо:    Vk gradT     T .       e     T  s  t   V t  Jq T  / T  0   e k   25 (15) Для малих деформацій, відповідно до законів термопружності, можна записати:   ,  e s   (16)  . T (17) Конструктивні закони рівнянь (16) та (17) виникають від виконання негативних нерівностей (15). Визначимо термодинамічні сили, пов'язані з внутрішніми змінними, наступним чином: 30 Ak    . Vk (18) Нерівність Клаузіуса-Дюгема (5) відображає той факт, що величина питомої виробництва ентропії є істотно позитивною: di s  dV 1 gradT   A k  Jq  0. dt T dt T T2 (19) 3 UA 100386 U Рівняння (19) можна розглядати також як добуток узагальнених термодинамічних сил    gradT  та узагальнених швидкостей Xi   , k ,  T2  T T термодинамічних потоків Ji  p ,  Vk ,  Jq :  процесів, що відбуваються, або  5 di s    i Ji . dt i 10 15 (20) Нерівноважна термодинаміка визначає, як термодинамічні сили Xi керують потоками Ji . Кожен із потоків залежить від будь-якої із сил або інтенсивних величин (наприклад, температури T), пов'язаних із дисипативними процесами під час деформації. Рівняння (19, 20) описують процес виробництва ентропії, який складається, по-перше, із розсіювання (дисипації) енергії внутрішнього тертя, в'язкопружної і пластичної деформації; подруге, невідновлювальної вільної енергії, що зберігається у матеріалі; і нарешті, розсіювання тепла за рахунок теплопровідності. Для багатьох деревних матеріалів невідновлювальна енергія становить лише 5-10 % від виробництва ентропії внаслідок механічного розсіювання, що дозволяє виконати спрощення: Ak Vk 1  0. t T (21) Таким чином рівняння (19) зводиться до наступного вигляду: ds  p gradT   Jq  0. dt T T2 (22) 20 Перший та другий закони термодинаміки, питома вільна енергія описана у рівняннях (4, 8, і 10), а також закон Фур'є ( Jq  k  gradT ) дозволяють прийти до наступного термомеханічної рівняння: k   2 T    Cp p dT   e , : T dt t T t (23) 25 де k - теплопровідність; Cp - теплоємність. Рівняння (23) виражає енергетичний баланс між чотирма її членами: передача тепла термостата за рахунок теплопровідності ( k   2 ); ефект уповільнення передачі тепла внаслідок 30 35 теплової інерції (   Cp dT ); внутрішня генерація теплового потоку, що складається із роботи dt  внутрішнього тертя, в'язкопружної і пластичної деформації, що перейшла у тепло ( Wp   : p ), t яка головним чином відповідає за підвищення середньої температури; та зміна (коливання) температури відносно її середнього значення під час циклічного деформування внаслідок  термопружного ефекту, We  T  e . T t Оскільки коливання температури, викликані термопружним ефектом, є незначні порівняно із зростанням середньої температури (фіг. 3), то виробленням тепла за рахунок роботи пружної деформації We можна знехтувати. Отже, рівняння (23) можна спростити: k   2 T    Cp 40 dT  Wp , dt (24) а рівняння (22) подати у вигляді: 4 UA 100386 U ds Wp gradT   Jq  0. dt T T2 (25) Таким чином загальна, сумарна величина ентропії втомного руйнування (ЕВР) може бути отримана шляхом інтегрування рівняння (25): 5 Sf  10 15 20 25 30 tf W  gradT p   T  Jq 2 dt ,   T  0  (26) де S f - ентропія втомного руйнування (ЕВР). Тобто в рівноважній теорії, еволюція нерівноважної ситуації задається нерівністю Клаузіуса, яке тим самим виконує роль динамічного рівняння. Для опису термодинамічних процесів в суто нерівноважних системах (в яких граничні умови перешкоджають встановленню термодинамічної рівноваги) необхідно трансформувати нерівність Клаузіуса в динамічні рівняння нерівноважних процесів. Для цього в прирощенні ентропії dS І. Пригожий запропонував виділити два члена [2]: dS  deS  diS , де de S - визначається кількістю поглиненого системою тепла (тобто характеризує ентропію отриману системою ззовні); diS - надлишок ентропії, виробленої незворотними процесами в самій системі. Згідно нерівності Клаузіуса, diS 0 або поклавши diS =(diS/dt)dt маємо: diS /dt0. Величина diS /dt є виробництво ентропії. Найбільш істотним моментом є те, що внесок у виробництво ентропії дають тільки незворотні процеси. Отже в системах, всередині яких протікають фізичні, хімічні, біологічні процеси, завжди ds виробляється ентропія. Це виробництво відбувається з певною швидкістю i  0 , де рівність dt нулю відповідає умові рівноваги. Виробництво ентропії в одиницю часу di s в одиниці об'єму відкритої системи дорівнює D за dt di s di s визначенням, тобто: D  і, отже,   DdV  0 . Визначимо функцію дисипації для нашого dtdV dt   випадку в наступному вигляді: D  dW  1  1  , де dW - це потік енергії ззовні всередину T dt  o T  dt  системи, тоді як рушійна сила цього потоку у виробництві ентропії являє собою градієнт   температури  1  1  , що виникає у процесі деформації між активаційним обсягом і T T  o  термостатом. При цьому W є енергією, що припадає на одиницю об'єму. Таким чином, загальне питоме виробництво ентропії втомного руйнування аж до повного руйнування може бути визначено таким: t dW  1 1  f 2  1 1  ,      T  T dt  DN  2  T  T N   o  0 dt  o де Sρ - загальна питома кількість ентропії, що вироблена при циклічному навантаженні за S    Дж  весь час до руйнування,  ;  м3     1 1  Дж    - дисипація енергії одиничного циклу навантаження,  ; T  T  м3     o  t p - час до руйнування, с; D 35 f 2 2E     2 - питома робота при деформації за один цикл навантаження, в зоні  2 2E 3 максимальних внутрішніх напружень, і деформацій, max , max , Дж/м ; W 5 UA 100386 U f - частота циклічного навантаження, (крім того вона визначає швидкість деформації і отже швидкість дисипації), c 1 ; Τ - температура саморозігріву в активаційному обсязі, в зоні максимальних внутрішніх напружень при циклічному деформуванні із заданими параметрами (f, max ), К; 5 10 15 Np  t p / f - число циклів до руйнування; To - температура термостату, К; max - максимальні внутрішні напруження в активаційному обсязі, МПа; Ε - модуль пружності, МПа. Багатьма дослідниками було відмічено, що під час проведення досліджень на втому деревини було помічено значне зростання температури у зоні надлому (руйнування) під дією циклічного навантаження. Великого значення цьому факту не надавали, вважалося, що "…вимірювання температури не може служити прискореним методом для визначення границі тривалості деревини" [3]. Пружність полімерних матеріалів носить нерівноважний характер, тобто під час циклічного навантаження відбуваються механічні втрати, що викликають тепловиділення в активаційному об'ємі зразка, що деформується, тобто його саморозігрів. Розігрів композиту під дією циклічного навантаження можна розглядати як процес + конкуренції між впливом температури на теплоприхід у процесі деформування, Q (T) та тепловідвід у навколишнє середовище Q (T): 20 dT  Q  T   Q  T  . dt (27) Враховуючи також перехресний вплив прийнятих до уваги ефектів, а саме, розширення тіла під час нагрівання та ефект виділення тепла під час деформування, отримаємо [4]: Q  T   T  T0    / 2 , (28) Q  T   T  T0  ,   hS / V , (29) (30) 25 30 де  - коефіцієнт пропорційності, що враховує особливості теплопередачі [3];  - коефіцієнт лінійного температурного розширення; h - коефіцієнт теплопередачі; S - площа поверхні зразка; VA - активаційний об'єм зразка; T0 - температура термостата у момент t=0;   f c  , ,E коефіцієнт пропорційності, що залежить від питомої теплоємності матеріалу c  , його щільності  та модуля пружності Е. Динамічну модель, яка описує еволюцію поведінки деревини в часі під час циклічного навантаження, наведено у вигляді системи диференціальних рівнянь, що враховують взаємний вплив температури, напруження та деформації в термоактиваційній зоні: 1  dT  dt  T  T0    2    T  T0    d  E  T  T E    Y  0  dt  Y  d .   T  T0   dt E   dY  dt   0 sinx    dx    dt  (31) 35 Результати машинного експерименту. Як об'єкт дослідження була прийнята вільха. Характеристики матеріалу: модуль пружності Ε=6810 МПа, межа міцності при згині  =83,4 6 UA 100386 U 3 5 10 15 20 25 30 35 40 45 1 МПа, щільність 750 кг/м ,  =0,00006 Κ ,  =100,  =0,0015. Початкові умови: t 0 =0; T0 =300 Κ;  0 =5 МПа;  0  0 / E ;  =1;  =2. Форма циклу навантаження згідно початковим умовам показана на фіг. 1 (Фіг. 1 - Форма циклічних коливань параметра Y(t) (максимальних локальних внутрішніх напружень) при заданих початкових умовах в режимі безперервного часу.). Рішення системи (31) методом Рунге-Кутта четвертого порядку показано на фіг. 2, 3, 4 у вигляді фазових траєкторій у режимі безперервного часу, що дозволяє простежити еволюцію системи (Фіг. 2 - Фазова діаграма залежності деформацій с(u) від діючих внутрішніх напружень в режимі сталого граничного циклу, аттрактора. Фіг. 3 - Підвищення середньої температури Т(і) в залежності від кількості циклів навантаження (динамічна модель). Фіг. 4 - Фазова діаграма залежності коливань температури Т(u) біля середньої температури від коливань напруг в стаціонарному стані, аттрактору). Діаграма роботи (гістерезисний еліпс, е(u) - залежність деформації від напруження), наведена на фіг. 2, відображає постійні витрати внутрішньої енергії у процесі періодичного деформування. Динаміка процесу протікає із відставанням деформації та температури від напруження. Причому частоти коливань всіх трьох параметрів (напруження, деформації та температури) у процесі еволюції системи стають рівними частоті вимушених коливань. У початковий момент еволюції, під дією циклічного навантаження, середня температура T(t) в активаційній зоні починає швидко підвищуватися (фіг. 3). Надалі вона стабілізується та приймає величину, що залежить від фізичних властивостей системи та параметрів навантаження. Як можна бачити із фіг. 2, 4, еволюція динамічної системи привела її в область сталого граничного циклу, аттрактора, в якому величини всіх внутрішніх параметрів (напруження, деформація та температура), що описують її поведінку, змінюються циклічно, та коливаються біля своїх середніх величин. При цьому, внаслідок зсуву фаз між напруженням та деформацією, робота пружних сил призводить до дисипації вільної енергії, вироблення теплоти та ентропії. У цьому стані теплопрохід дорівнює тепловідводу, що дозволяє системі знаходиться у стаціонарному стані. При цьому прихід енергії ззовні системи дорівнює її витраті всередині. Результати натурного експерименту. Зразки із вільхи, січенням 25,5×9,5 мм, закріплювалися консольно на спеціальній установці. Вільний кінець консолі сприймав циклічне навантаження. Зміна величин внутрішніх напружень виконувалася зміною довжини консолі при постійній величині амплітуди коливань. Межа міцності при згині та модуль пружності визначалися за стандартною методикою. Для цього установку із зразком встановлювали на розривну машину Р5 при параметрах: u  =83,4 МПа, Ε=6810 МПа. Вимірювання температури відбувалося термопарами, що знаходилася на зовнішній поверхні консолі у місцях її жорсткою закріплення. Температуру реєстрували на комп'ютері через кожних 10 с. Коливання віднулеві. У таблиці наведені умови та результати експериментів. Підвищення температури показано у зоні стиску. На підставі даних таблиці побудовані графіки залежності підвищення температури при різних параметрах навантаження (Фіг. 5 - Графік залежності максимального підвищення абсолютної температури в активаційній зоні від частоти коливань. Фіг. 6 - Графік залежності максимального підвищення абсолютної температури в активаційній зоні від максимальної напруги в активаційному об'ємі). Графік залежності загальної питомої ентропії, що вироблена у процесі втомного руйнування вільхи наведено на фіг. 7. Як випливає із таблиці, обидва фактори: внутрішні напруження та частота коливань, істотно впливають на підвищення температури. Крім того було встановлено, що питома ентропія втомного руйнування не залежить від умов навантаження, а залежить тільки від властивостей матеріалу. 50 7 UA 100386 U Таблиця змінних факторів та результати експериментів. Максимальна Температура в зоні Число Питома ентропія напруга в Частота Температура максимальних циклів до втомного № активаційному коливань, термостата, напружень в руйнування, руйнування вільхи, об'ємі при f, Гц Т0,°К стаціонарному Np Sp, [MJ/m3*K] згині,  , МРа стані, Т,°К 1 2 3 4 5 6 7 1 38,8 1,3 293 298 3,59Е+05 2,999 2 38,8 2,7 293 301 1,13E+05 2,985 3 47,9 4,0 293 305 3,33Е+04 3,015 4 47,9 5,3 293 308 2,02Е+04 2,896 5 60,7 6,6 293 313 7,66Е+03 3,112 6 60,7 8 293 316 5,61Е+03 2,986 5 10 15 20 25 30 35 40 Під час порівняння результатів, що отримані у натурному експерименті (фіг. 5, 6), із результатами машинного моделювання (фіг. 3), видно, що динамічна модель (31) не тільки якісно описує поведінку матеріалу в часі, що досліджувався, але й дуже близька до його кількісному опису. Загальний характер зміни температури у зоні дії максимальних напружень (наприклад, в зоні жорсткого закладення консолі) у машинному та натурному експериментах приводить до висновку, що для кожного матеріалу існує своя температура його максимального розігріву, за даних умов навантаження. Ці умови визначаються обмеженим числом керуючих параметрів, (максимальні напруження та частота, тобто швидкість зміни напруження в активаційному об'ємі), що переводять динамічну систему при опорі втоми, в область сталого граничного циклу, аттрактора. Корисна модель ґрунтується на парадигмі сталості величини накопиченого виробництва ентропії до моменту руйнування, Sp. Тобто, іншими словами, сталості запасу виробництва ентропії. А це передбачає, що термодинамічні умови, пов'язані з виробництвом ентропії, тобто умови деградації матеріалу, залишаються ідентичними в процесі опору матеріалу втоми, і залежать тільки від часу. Тобто руйнування відбувається в момент, коли вичерпається весь запас ентропії. У межах проведених натурних випробувань було виявлено, що питома ентропія втомного руйнування (УЕВР) залежить тільки від дисипативних властивостей матеріалу і не залежить від навантаження, частоти і розмірів деталі. Таким чином, тривалість процесу опору матеріалу втоми, тобто його деградація, може бути визначена, якщо відома питома ентропія втомного руйнування даного матеріалу. Наприклад, для прогнозування гранично допустимого числа циклів навантаження при експлуатації деталей з деревини вільхи на опір втоми спосіб реалізували наступним чином. Деталь з вільхи розміром 259,5160 мм експлуатується в умовах віднульового циклічного навантаження при її жорсткому консольному закріпленні. Максимальні напруги в деталі складають max =10 МРа, частота віднульових коливань вільного кінця консолі f=1 Гц. Температура навколишнього середовища (термостата) дорівнює T0 =293°К. При роботі деталі, при переході її в новий стаціонарний стан, температура в зоні кріплення піднімається до Τ=298°К. Модуль пружності матеріалу Ε=8410 МПа. Шляхом попередньо проведених випробувань була визначена величина питомої ентропії втомного руйнування вільхи, яка 3 представлена в таблиці. Вона склала величину рівну Sρ=2,999±0,011 МДж/м К. Користуючись формулою винаходу визначаємо допустиме число циклів навантаження при коефіцієнті запасу рівному k=0,8: S S 2999000 Ni   k   k 2   0,8  13  106. , 2 Di f  1 1  1 10  1012  1 1        2E  T0 T  2  8410000000 293 298    На основі парадигми термодинаміки деградації матеріалу при його опору втомі можна проводити прискорені втомні випробування за рахунок підвищення швидкості процесу деградації Ji при збереженні еквівалентних термодинамічних сил Хі, щоб отримати ту ж послідовність фізичних процесів, в однакових пропорціях, але з більшою інтенсивністю. Наприклад, за рахунок збільшення частоти прикладеного циклічного навантаження швидкість 8 UA 100386 U 5 10 деградації матеріалу збільшується, а тривалість випробувань відповідно буде зменшуватися. Це дозволяє значно знизити час випробувань на опір втомі. З іншого боку, контролюючи час перебування матеріалу під навантаженням і вимірюючи при цьому витрати ентропії втомного руйнування, можна визначити гранично допустимий час роботи матеріалу. Джерела інформації: 1. Одинг И.А. Допускаемые напряжения в машиностроении и циклическая прочность металлов. / И.А. Одинг / М., Машиностроение, 1962, 350 с. 2. Пригожий И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур. И. Пригожий, Д. Кондепуди. - М.: Мир, 2009. - 461 с. 3. Бєлянкін Ф.П. Міцність деревини під впливом повторного навантаження. [Монографія] / Ф.П. Бєлянкін. - К.: Видавництво Академії Наук України, 1936. - 120 с. 4. Петров В.А. Физические основы прогнозирования долговечности конструкционных материалов. / В.А. Петров, А.Я. Башкарев, В.И. Веттергень. - СПб.: Политехника, 1993. - 475 с. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 15 20 25 Спосіб неруйнівного контролю та прогнозування довговічності деталей з деревини і деревних композиційних матеріалів при їх циклічному навантаженні, що включає порівняння ресурсу контрольованої деталі зі стовідсотковим ресурсом аналогічної деталі, який відрізняється тим, що як запобіжне порівняння приймають величину питомої кількості виробленої ентропії в перебігу часу, що пройшов з моменту початку експлуатації деталі, причому максимальне питоме виробництво ентропії для матеріалу, з якого виготовлена контрольована деталь, визначається експериментально, шляхом її циклічного навантаження при внутрішніх напруженнях і частотах навантаження, що перевищують частоти і навантаження, при яких відбувається експлуатація деталі, при цьому величина загально питомого запасу виробництва ентропії втомного руйнування визначається за формулою: f 2  1 1      , 2  o     де S - загальна питома кількість ентропії, що вироблена при циклічному навантаженні за весь  Дж  час до руйнування,  ;  м3    S  D   30 D 2 2 f 2 2  1 1  Дж    ;      - дисипація енергії одиничного циклу навантаження,  3 м     o  - питома робота при деформації за один цикл навантаження, в зоні максимальних внутрішніх напружень, і деформацій, mах, mах, Дж/м ; f - частота циклічного навантаження, (крім того вона визначає швидкість деформації і, отже, -1 швидкість дисипації), с ; Τ - температура саморозігріву в активаційному обсязі, в зоні максимальних внутрішніх напружень при циклічному деформуванні із заданими параметрами (f, mах), К; Np=tp/f - число циклів до руйнування; Тo - температура термостату, К; max - максимальні внутрішні напруження в активаційному обсязі, МПа; Ε - модуль пружності, МПа; причому ресурс вважається вичерпаним в разі досягнення числа циклів, що визначається за формулою: 3 35 40  i   k 45 S Di , де k=0,5-0,6 - коефіцієнт запасу; i  - гранично допустима кількість циклів навантаження при заданих параметрах циклічного навантаження (fi, i max: i max), і при температурі саморозігріву, рівній Т і; Di - дисипація енергії одиничного циклу навантаження при конкретних умовах експлуатації D i,(fi, i max, Тi, To). 9 UA 100386 U 10 UA 100386 U 11 UA 100386 U 12 UA 100386 U Комп’ютерна верстка М. Шамоніна Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 13