Спосіб визначення потокозчеплень ротора й швидкості частотно-регульованого асинхронного двигуна
Номер патенту: 39949
Опубліковано: 25.03.2009
Автори: Скалько Юрій Сергійович, Волков Олександр Васильович
Формула / Реферат
1. Спосіб визначення потокозчеплень ротора й швидкості частотно-регульованого асинхронного двигуна, який полягає у тому, що контролюють проекції узагальнених векторів статорної напруги й струму двигуна на осі нерухомої ортогональної координатної системи "![]() ", пов'язаної віссю "
", пов'язаної віссю "![]() " з геометричною віссю статорної обмотки фази "А" двигуна, обчислюють проекції узагальненого вектора ЕРС ротора двигуна на осі "
" з геометричною віссю статорної обмотки фази "А" двигуна, обчислюють проекції узагальненого вектора ЕРС ротора двигуна на осі "![]() " і "
" і "![]() " зазначеної нерухомої ортогональної координатної системи у вигляді діленої на коефіцієнт зв'язку ротора різниці проекції узагальненого вектора статорної напруги на відповідну вісь даної координатної системи й двох від'ємників, перший з яких дорівнює добутку активного опору статорної обмотки двигуна на значення проекції узагальненого вектора статорного струму на цю ж вісь нерухомої ортогональної координатної системи, а другий - добутку сумарної індуктивності розсіювання двигуна на похідну за часом від тієї ж проекції узагальненого вектора статорного струму, розраховують проекції U
" зазначеної нерухомої ортогональної координатної системи у вигляді діленої на коефіцієнт зв'язку ротора різниці проекції узагальненого вектора статорної напруги на відповідну вісь даної координатної системи й двох від'ємників, перший з яких дорівнює добутку активного опору статорної обмотки двигуна на значення проекції узагальненого вектора статорного струму на цю ж вісь нерухомої ортогональної координатної системи, а другий - добутку сумарної індуктивності розсіювання двигуна на похідну за часом від тієї ж проекції узагальненого вектора статорного струму, розраховують проекції U![]() , U
, U![]() узагальненого вектора напруги ротора на осі "
узагальненого вектора напруги ротора на осі "![]() " і "
" і "![]() " нерухомої ортогональної координатної системи шляхом вирахування із проекцій Е
" нерухомої ортогональної координатної системи шляхом вирахування із проекцій Е![]() , Е
, Е узагальненого вектора ЕРС ротора добутків, обчислених у результаті множення проекцій
![]() ,
, ![]() узагальненого вектора статорного струму на коефіцієнт
узагальненого вектора статорного струму на коефіцієнт ![]() :
:
![]() , (1)
, (1)
через визначені значення проекцій ![]()
![]() узагальненого вектора потокозчеплення ротора двигуна й розраховані проекції узагальненого вектора напруги ротора знаходять швидкість двигуна зі співвідношення:
узагальненого вектора потокозчеплення ротора двигуна й розраховані проекції узагальненого вектора напруги ротора знаходять швидкість двигуна зі співвідношення:
![]() , (2)
, (2)
через визначені значення швидкості й проекцій узагальненого вектора напруги ротора й задане зворотне значення q електромагнітної постійної часу ротора обчислюють оцінні значення проекцій ![]()
![]() узагальненого вектора потокозчеплення ротора двигуна із залежностей:
узагальненого вектора потокозчеплення ротора двигуна із залежностей:
![]() , (3)
, (3)
який відрізняється тим, що проекції ![]()
![]() узагальненого вектора потокозчеплення ротора двигуна визначають у результаті інтегрування за часом t різниці проекцій Е
узагальненого вектора потокозчеплення ротора двигуна визначають у результаті інтегрування за часом t різниці проекцій Е![]() , Е
, Е![]() узагальненого вектора ЕРС ротора й керуючих сигналів F
узагальненого вектора ЕРС ротора й керуючих сигналів F![]() , F
, F![]() :
:
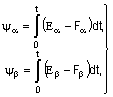 , (4)
, (4)
при цьому контролюють відхилення ![]()
![]()
![]()
![]() між визначеними й оцінними значеннями проекцій узагальненого вектора потокозчеплення ротора:
між визначеними й оцінними значеннями проекцій узагальненого вектора потокозчеплення ротора:
![]() , (5)
, (5)
пропорційно значенням яких формують згадані керуючі сигнали F![]() , F
, F![]() , а зазначений коефіцієнт
, а зазначений коефіцієнт ![]() обчислюють у вигляді добутку індуктивності намагнічування двигуна на зворотне значення його електромагнітної постійної часу ротора.
обчислюють у вигляді добутку індуктивності намагнічування двигуна на зворотне значення його електромагнітної постійної часу ротора.
2. Спосіб за п. 1, який відрізняється тим, що обчислюють уточнені значення проекцій E![]() *, E
*, E![]() * узагальненого вектора ЕРС ротора шляхом множення на корегувальний коефіцієнт
* узагальненого вектора ЕРС ротора шляхом множення на корегувальний коефіцієнт ![]() визначених проекцій Е
визначених проекцій Е![]() , Е
, Е![]() узагальненого вектора ЕРС ротора двигуна:
узагальненого вектора ЕРС ротора двигуна:
![]() , (6)
, (6)
при цьому розраховують значення косинуса й синуса від аргументу ![]() узагальненого вектора статорного струму двигуна в результаті ділення відповідно проекцій
узагальненого вектора статорного струму двигуна в результаті ділення відповідно проекцій ![]() ,
, ![]() узагальненого вектора статорного струму на корінь квадратний із суми квадратів зазначених проекцій:
узагальненого вектора статорного струму на корінь квадратний із суми квадратів зазначених проекцій:
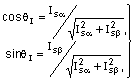 , (7)
, (7)
визначають уточнене значення проекції Ev* узагальненого вектора ЕРС ротора двигуна на вісь "v" обертової ортогональної координатної системи "u-v", орієнтованої віссю "u" за узагальненим вектором статорного струму, у вигляді:
![]() (8)
(8)
контролюють кутову частоту ![]() узагальненого вектора потокозчеплення ротора двигуна й визначають оцінні значення Е'
узагальненого вектора потокозчеплення ротора двигуна й визначають оцінні значення Е'![]() , Е'
, Е'![]() проекцій узагальненого вектора ЕРС ротора двигуна із залежностей:
проекцій узагальненого вектора ЕРС ротора двигуна із залежностей:
![]() (9)
(9)
обчислюють оцінне значення E'v проекції узагальненого вектора ЕРС ротора двигуна на вісь "v" обертової ортогональної координатної системи "u-v" зі співвідношення:
![]() (10)
(10)
а значення корегувального коефіцієнта ![]() визначають у результаті виділення постійної складової із сигналу, обчисленого у вигляді частки від ділення згаданих уточненої й оцінної проекцій узагальненого вектора ЕРС ротора на вісь "v" обертової ортогональної координатної системи "u-v".
визначають у результаті виділення постійної складової із сигналу, обчисленого у вигляді частки від ділення згаданих уточненої й оцінної проекцій узагальненого вектора ЕРС ротора на вісь "v" обертової ортогональної координатної системи "u-v".
3. Спосіб за п. 1, який відрізняється тим, що обчислюють модуль ![]() узагальненого вектора потокозчеплення ротора двигуна у вигляді кореня квадратного із суми квадратів визначених проекцій
узагальненого вектора потокозчеплення ротора двигуна у вигляді кореня квадратного із суми квадратів визначених проекцій ![]()
![]() цього вектора на осі "
цього вектора на осі "![]() " і "
" і "![]() " нерухомої ортогональної координатної системи, розраховують значення косинуса й синуса від аргументу
" нерухомої ортогональної координатної системи, розраховують значення косинуса й синуса від аргументу ![]() узагальненого вектора потокозчеплення ротора шляхом ділення відповідно проекцій
узагальненого вектора потокозчеплення ротора шляхом ділення відповідно проекцій ![]()
![]() на модуль узагальненого вектора потокозчеплення ротора, визначають проекції узагальненого вектора ЕРС ротора й статорного струму двигуна на вісь "х" обертової ортогональної координатної системи "х-у", орієнтованою віссю "х" за узагальненим вектором потокозчеплення ротора двигуна, у вигляді відповідно:
на модуль узагальненого вектора потокозчеплення ротора, визначають проекції узагальненого вектора ЕРС ротора й статорного струму двигуна на вісь "х" обертової ортогональної координатної системи "х-у", орієнтованою віссю "х" за узагальненим вектором потокозчеплення ротора двигуна, у вигляді відповідно:
![]() (11)
(11)
розраховують інтеграли И1, И2 за часом за однаковий часовий інтервал ![]() від абсолютного значення проекції Ех узагальненого вектора ЕРС ротора й від абсолютного значення різниці між модулем
від абсолютного значення проекції Ех узагальненого вектора ЕРС ротора й від абсолютного значення різниці між модулем ![]() узагальненого вектора потокозчеплення ротора й добутком індуктивності Lm намагнічування двигуна на проекцію Isx узагальненого вектора статорного струму:
узагальненого вектора потокозчеплення ротора й добутком індуктивності Lm намагнічування двигуна на проекцію Isx узагальненого вектора статорного струму:
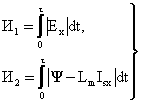 , (12)
, (12)
а зворотне значення q електромагнітної постійної часу ротора двигуна задають у вигляді частки від ділення зазначених інтегралів.
Текст
УКРАЇНА (19) UA (11) 39949 (13) U (51) МПК (2009) H02P 21/00 МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ДЕРЖАВНИЙ ДЕПАРТАМЕНТ ІНТЕЛЕКТУАЛЬНОЇ ВЛАСНОСТІ ОПИС видається під відповідальність власника патенту ДО ПАТЕНТУ НА КОРИСНУ МОДЕЛЬ (54) СПОСІБ ВИЗНАЧЕННЯ ПОТОКОЗЧЕПЛЕНЬ РОТОРА Й ШВИДКОСТІ ЧАСТОТНО-РЕГУЛЬОВАНОГО АСИНХРОННОГО ДВИГУНА 1 коефіцієнт : U E Is , , U E Is (1) через визначені значення проекцій , узагальненого вектора потокозчеплення ротора двигуна й розраховані проекції узагальненого вектора ротора двигуна із залежностей: ' U qU / 2 q2 , , (3) ' U qU / 2 q2 який відрізняється тим, що проекції , узагальненого вектора потокозчеплення ротора двигуна визначають у результаті інтегрування за часом t різниці проекцій Е , Е узагальненого вектора ЕРС ротора й керуючих сигналів F , F : t (4) , F dt 0 при цьому контролюють відхилення , між визначеними й оцінними значеннями проекцій узагальненого вектора потокозчеплення ротора: ' , , (5) ' 0 t пропорційно значенням яких формують згадані керуючі сигнали F , F , а зазначений коефіцієнт обчислюють у вигляді добутку індуктивності намагнічування двигуна на зворотне значення його електромагнітної постійної часу ротора. 2. Спосіб за п. 1, який відрізняється тим, що обчислюють уточнені значення проекцій E *, E * узагальненого вектора ЕРС ротора шляхом множення на корегувальний коефіцієнт визначених U 39949 F dt, (11) (13) UA обчислених у результаті множення проекцій s , s узагальненого вектора статорного струму на напруги ротора знаходять швидкість двигуна зі співвідношення: 2 U U / 2 ,(2) через визначені значення швидкості й проекцій узагальненого вектора напруги ротора й задане зворотне значення q електромагнітної постійної часу ротора обчислюють оцінні значення проекцій , узагальненого вектора потокозчеплення (19) (21) u200809286 (22) 16.07.2008 (24) 25.03.2009 (46) 25.03.2009, Бюл.№ 6, 2009 р. (72) ВОЛКОВ ОЛЕКСАНДР ВАСИЛЬОВИЧ, СКАЛЬКО ЮРІЙ СЕРГІЙОВИЧ (73) ЗАПОРІЗЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ (57) 1. Спосіб визначення потокозчеплень ротора й швидкості частотно-регульованого асинхронного двигуна, який полягає у тому, що контролюють проекції узагальнених векторів статорної напруги й струму двигуна на осі нерухомої ортогональної координатної системи " ", пов'язаної віссю " " з геометричною віссю статорної обмотки фази "А" двигуна, обчислюють проекції узагальненого вектора ЕРС ротора двигуна на осі " " і " " зазначеної нерухомої ортогональної координатної системи у вигляді діленої на коефіцієнт зв'язку ротора різниці проекції узагальненого вектора статорної напруги на відповідну вісь даної координатної системи й двох від'ємників, перший з яких дорівнює добутку активного опору статорної обмотки двигуна на значення проекції узагальненого вектора статорного струму на цю ж вісь нерухомої ортогональної координатної системи, а другий - добутку сумарної індуктивності розсіювання двигуна на похідну за часом від тієї ж проекції узагальненого вектора статорного струму, розраховують проекції U , U узагальненого вектора напруги ротора на осі " " і " " нерухомої ортогональної координатної системи шляхом вирахування із проекцій Е , Е узагальненого вектора ЕРС ротора добутків, 2 3 39949 4 проекцій Е , Е узагальненого вектора ЕРС ротора двигуна: , , (6) при цьому розраховують значення косинуса й синуса від аргументу θІ узагальненого вектора статорного струму двигуна в результаті ділення відповідно проекцій s , s узагальненого вектора неного вектора ЕРС ротора на вісь "v" обертової ортогональної координатної системи "u-v". 3. Спосіб за п. 1, який відрізняється тим, що обчислюють модуль узагальненого вектора потокозчеплення ротора двигуна у вигляді кореня квадратного із суми квадратів визначених проекцій , цього вектора на осі " " і " " нерухомої статорного струму на корінь квадратний із суми квадратів зазначених проекцій: cos s 2 2 , s s , (7) s sin 2 2 s s узагальненого вектора потокозчеплення ротора шляхом ділення відповідно проекцій , на модуль узагальненого вектора потокозчеплення ротора, визначають проекції узагальненого вектора ЕРС ротора й статорного струму двигуна на вісь "х" обертової ортогональної координатної системи "х-у", орієнтованою віссю "х" за узагальненим вектором потокозчеплення ротора двигуна, у вигляді відповідно: x cos sin , , (11) sx s cos s sin визначають уточнене значення проекції Ev* узагальненого вектора ЕРС ротора двигуна на вісь "v" обертової ортогональної координатної системи "uv", орієнтованої віссю "u" за узагальненим вектором статорного струму, у вигляді: cos sin , (8) v контролюють кутову частоту узагальненого вектора потокозчеплення ротора двигуна й визначають оцінні значення Е' , Е' проекцій узагальненого вектора ЕРС ротора двигуна із залежностей: ' , , (9) ' обчислюють оцінне значення E'v проекції узагальненого вектора ЕРС ротора двигуна на вісь "v" обертової ортогональної координатної системи "uv" зі співвідношення: 'v ' cos ' sin , (10) ортогональної координатної системи, розраховують значення косинуса й синуса від аргументу розраховують інтеграли И1, И2 за часом за однаковий часовий інтервал від абсолютного значення проекції Ех узагальненого вектора ЕРС ротора й від абсолютного значення різниці між модулем узагальненого вектора потокозчеплення ротора й добутком індуктивності Lm намагнічування двигуна на проекцію Isx узагальненого вектора статорного струму: И1 E x dt, 0 (12) , И2 LmIsx dt 0 а зворотне значення q електромагнітної постійної часу ротора двигуна задають у вигляді частки від ділення зазначених інтегралів. а значення корегувального коефіцієнта визначають у результаті виділення постійної складової із сигналу, обчисленого у вигляді частки від ділення згаданих уточненої й оцінної проекцій узагаль Корисна модель відноситься до галузі електротехніки, а саме – до частотно-регульованих асинхронних електроприводів з векторним керуванням, у яких поточні значення потокозчеплень ротора й швидкості двигуна визначаються непрямим способом через його статорні напруги й струми. Непряме визначення потокозчеплень і швидкості асинхронного двигуна (через згадані його статорні напруги й струми) дозволяє виключити встановлення додаткових датчиків усередині (датчиків магнітного потоку або вимірювальних обмоток ЕРС) або на валу (швидкості, положення ротора) двигуна, що, у свою чергу, спрощує конструкцію двигуна (не вимагає переробки серійного двигуна або виготовлення його із двома кін цями вала) та підвищує експлуатаційну надійність (через відсутність датчиків у повітряному зазорі або на валу двигуна) частотно-регульованого асинхронного електропривода в цілому, а також – розширює область застосування зазначеного електропривода на запилені, агресивні та вибухонебезпечні середовища. Відомий з [1] спосіб визначення потокозчеплень ротора частотно-регульованого асинхронного двигуна, який полягає у тому, що контролюють проекції узагальнених векторів статорної напруги й струму двигуна на осі нерухомої ортогональної координатної системи «α–β», пов'язаною віссю «α» с геометричною віссю статорної обмотки фази «А» двигуна, обчислюють проекції узагальненого вектора ЕРС статора двигуна на осі «α» і «β» за 5 значеної нерухомої ортогональної координатної системи у вигляді різниці проекції узагальненого вектора статорної напруги на відповідну вісь координатної системи й добутку активного опору статорної обмотки двигуна на поточне значення проекції узагальненого вектора статорного струму на ту ж вісь нерухомої ортогональної координатної системи, за допомогою аперіодичних ланок розраховують через обчислені проекції узагальненого вектора ЕРС статора на осі «α» і «β» координатної системи проекції узагальненого вектора потокозчеплення статора двигуна на відповідні осі нерухомої ортогональної координатної системи, віднімаючи з останніх добутки сумарної індуктивності розсіювання статора двигуна на поточне значення проекції узагальненого вектора статорного струму двигуна, визначають поточні значення проекцій узагальненого вектора потокозчеплення ротора на осі «α» і «β» нерухомої координатної системи. Недоліком відомого способу є невисока точність визначення проекцій узагальненого вектора потокозчеплення ротора двигуна, обумовлена тим, що в цьому способі із проекцій узагальненого вектора ЕРС статора здійснюється знаходження проекцій узагальненого вектора потокозчеплення статора за допомогою аперіодичних ланок, а не – шляхом інтегрування (як необхідно при точному розрахунку проекцій потокозчеплень статора). У той же час застосування ідеального інтегрування у відомому способі на практиці виявляється неможливим внаслідок виникнення помилки, що накопичується, у існуючих інтеграторів (яка призводить також до помилки у визначенні проекцій потокозчеплення ротора, у тому числі – у вигляді зсуву нульового рівня, і, як наслідок, до порушення нормального функціонування способу). У свою чергу, через похибку при визначенні проекцій узагальненого вектора потокозчеплення ротора двигуна в частотно-регульованих асинхронних електроприводах з векторним керуванням відбувається порушення координатної орієнтації обертової ортогональної координатної системи (орієнтованої зазвичай за узагальненим вектором потокозчеплення ротора, у якій відбувається регулювання електромагнітних параметрів режиму двигуна), внаслідок чого знижується якість регулювання електромеханічних процесів привода. Найбільш близьким за технічною сутністю до запропонованого способу є спосіб визначення потокозчеплень ротора й швидкості частотнорегульованого асинхронного двигуна [2], який полягає у тому, що контролюють проекції узагальнених векторів статорної напруги й струму двигуна на осі нерухомої ортогональної координатної системи «α–β», пов'язаної віссю «α» с геометричною віссю статорної обмотки фази «А» двигуна, обчислюють проекції узагальненого вектора ЕРС ротора двигуна на осі «α» і «β» зазначеної нерухомої ортогональної координатної системи у вигляді діленої на коефіцієнт зв'язку ротора різниці проекції узагальненого вектора статорної напруги на відповідну вісь даної координатної системи й двох від'ємників, перший з яких дорівнює добутку активного опору статорної обмотки двигуна на значення проекції узагальненого вектора статорного струму 39949 6 на цю же вісь нерухомої ортогональної координатної системи, а другий – добутку сумарної індуктивності розсіювання двигуна на похідну за часом від тієї ж проекції узагальненого вектора статорного струму, розраховують проекції Uα, Uβ узагальненого вектора напруги ротора на осі «α» і «β» нерухомої ортогональної координатної системи шляхом віднімання із проекцій Eα, Eβ узагальненого вектора ЕРС ротора добутків, обчислених у результаті множення проекцій Isα, Isβ узагальненого вектора статорного струму на активний опір ротора Rr і коефіцієнт зв'язку ротора k двигуна: U E k Rr Is , U E k Rr Is (1) визначають проекції Ψα, Ψβ узагальненого вектора потокозчеплення ротора й швидкість ω двигуна в результаті розв'язання для кожного поточного моменту часу системи рівнянь: U U T 2 1 T 2 , U U T 2 1 T 2 , , (2) 2 2 U U де T – електромагнітна постійна часу ротора двигуна. До переваг відомого способу відноситься знаходження в ньому проекцій узагальненого вектора потокозчеплення ротора й швидкості в загальноприйнятій (для машин змінного струму) системі відносних одиниць [3], що скорочує й нормує межі зміни обумовлених параметрів, за рахунок чого може бути зменшена розрядність застосовуваного обчислювача. Недоліком відомого способу є відносна громіздкість виконуваних обчислень при функціонуванні даного способу, обумовлена використовуваним у ньому чисельним (ітераційним) методом розрахунку поточних значень параметрів, що визначаються, у кожній часовій точці розрахунку. В основу корисної моделі поставлене завдання розробки більш простого в технічній реалізації способу визначення потокозчеплень ротора й швидкості частотно-регульованого асинхронного двигуна, за допомогою якого досягається здешевлення системи автоматичного керування частотнорегульованих асинхронних електроприводів при збереженні високої точності регулювання зазначених параметрів режиму двигуна. Вирішення цього завдання досягається тим, що в способі визначення потокозчеплень ротора й швидкості частотно-регульованого асинхронного двигуна контролюють проекції узагальнених векторів статорної напруги й струму двигуна на осі нерухомої ортогональної координатної системи «α–β», пов'язаної віссю «α» с геометричною віссю статорної обмотки фази «А» двигуна, обчислюють проекції узагальненого вектора ЕРС ротора двигуна на осі «α» і «β» зазначеної нерухомої ортогональної координатної системи у вигляді діленої на коефіцієнт зв'язку ротора різниці проекції узагальненого вектора статорної напруги на відповідну вісь даної координатної системи й двох від'ємни 7 ків, перший з яких дорівнює добутку активного опору статорної обмотки двигуна на значення проекції узагальненого вектора статорного струму на цю же вісь нерухомої ортогональної координатної системи, а другий – добутку сумарної індуктивності розсіювання двигуна на похідну за часом від тієї ж проекції узагальненого вектора статорного струму, розраховують проекції Uα, Uβ узагальненого вектора напруги ротора на осі «α» і «β» нерухомої ортогональної координатної системи шляхом віднімання із проекцій Eα, Eβ узагальненого вектора ЕРС ротора добутків, обчислених у результаті множення проекцій Isα, Isβ узагальненого вектора статорного струму на коефіцієнт : U E Is , (3) , U E Is через визначені значення проекцій Ψα, Ψβ узагальненого вектора потокозчеплення ротора двигуна й розраховані проекції узагальненого вектора напруги ротора знаходять швидкість двигуна зі співвідношення: 2 2 U U , (4) через визначені значення швидкості й проекцій узагальненого вектора напруги ротора й задане зворотне значення q електромагнітної постійної часу ротора обчислюють оцінні значення проекцій , узагальненого вектора потокозчеплення ротора двигуна із залежностей: 2 q2 , (5) , 2 q2 U qU додатково проекції Ψα, Ψβ узагальненого вектора потокозчеплення ротора двигуна визначають у результаті інтегрування за часом t різниці проекцій Eα, Eβ узагальненого вектора ЕРС ротора й керуючих сигналів Fα, Fβ: t E F dt, 0 (6) , t E F dt 0 при цьому контролюють відхилення ΔΨα, ΔΨβ між визначеними й оцінними значеннями проекцій узагальненого вектора потокозчеплення ротора: , , (7) пропорційно значенням яких формують згадані керуючі сигнали Fα і Fβ, а зазначений коефіцієнт обчислюють у вигляді добутку індуктивності намагнічування двигуна на зворотне значення його електромагнітної постійної часу ротора. Для підвищення точності визначення потокозчеплень ротора двигуна додатково обчислюють * уточнені значення проекцій E* , E узагальненого вектора ЕРС ротора шляхом множення на корегувальний коефіцієнт ξ визначених проекцій Eα, Eβ U qU 39949 8 узагальненого вектора ЕРС ротора двигуна: E* E , , * E E (8) при цьому розраховують значення косинуса й синуса від аргументу θI узагальненого вектора статорного струму двигуна в результаті ділення відповідно проекцій Isα, Isβ узагальненого вектора статорного струму на корінь квадратний із суми квадратів зазначених проекцій: cos I Is I2 I2 , s s (9) , sin I Is I2 I2 s s визначають уточнене значення проекції E* v узагальненого вектора ЕРС ротора двигуна на вісь «v» обертової ортогональної координатної системи «u–v», орієнтованою віссю «u» за узагальненим вектором статорного струму, у вигляді: * (10) E* E cos I E* sin I , v контролюють кутову частоту ωΨ узагальненого вектора потокозчеплення ротора двигуна й визначають оцінні значення E , E проекцій узагаль неного вектора ЕРС ротора двигуна із залежностей: E , (11) , E обчислюють оцінне значення Ev проекції узагальненого вектора ЕРС ротора двигуна на вісь «v» обертової ортогональної координатної системи «u–v» зі співвідношення: E E cos I E sin I , (12) v а значення корегувального коефіцієнта визначають у результаті виділення постійної складової із сигналу, обчисленого у вигляді частки від ділення згаданих уточненої й оцінної проекцій узагальненого вектора ЕРС ротора на вісь «v» обертової ортогональної координатної системи «u–v». Для підвищення точності визначення швидкості двигуна додатково обчислюють модуль Ψ узагальненого вектора потокозчеплення ротора двигуна у вигляді кореня квадратного із суми квадратів визначених проекцій Ψα, Ψβ цього вектора на осі «α» і «β» нерухомої ортогональної координатної системи, розраховують значення косинуса й синуса від аргументу θΨ узагальненого вектора потокозчеплення ротора шляхом ділення відповідно проекцій Ψα і Ψβ на модуль узагальненого вектора потокозчеплення ротора, визначають проекції узагальненого вектора ЕРС ротора й статорного струму двигуна на вісь «x» обертової ортогональної координатної системи «x–y», орієнтованої віссю «x» за узагальненим вектором потокозчеплення ротора двигуна, у вигляді відповідно: 9 E x E cos E sin , , Isx Is cos Is sin 39949 (13) розраховують інтеграли И1, И2 за часом за однаковий часовий інтервал від абсолютного значення проекції Ex узагальненого вектора ЕРС ротора й від абсолютного значення різниці між модулем Ψ узагальненого вектора потокозчеплення ротора й добутком індуктивності Lm намагнічування двигуна на проекцію Isx узагальненого вектора статорного струму: И1 E x dt, 0 (14) , И2 LmIsx dt 0 а зворотне значення q електромагнітної постійної часу ротора двигуна задають у вигляді частки від ділення зазначених інтегралів. У запропонованому способі визначення проекцій узагальненого вектора потокозчеплення ротора й швидкості двигуна здійснюється з використанням відносно простих операцій обчислення. По-перше, – керуючих сигналів Fα, Fβ, пропорційних відхиленням між визначеними Ψα, Ψβ і оцінни ми , значеннями проекцій узагальненого вектора потокозчеплення ротора (які формуються, наприклад, за допомогою пропорційних або пропорційно-інтегральних ланок). По-друге, – інтегралів за часом від різниць між проекціями Eα, Eβ узагальненого вектора ЕРС ротора й згаданих керуючих сигналів Fα, Fβ. За рахунок цього виключається ітераційна (циклічна) послідовність розрахунку на кожному часовому кроці розрахунку й забезпечується скорочення загального числа обчислювальних операцій, а також – зменшення загального часу розрахунку, що, у свою чергу, дозволяє знизити вимоги до обчислювальної потужності й швидкодії застосовуваного в системі автоматичного керування обчислювача, а, отже, – зменшити вартість системи автоматичного керування електроприводом і частотно-регульованим асинхронним електроприводом у цілому. Таким чином, нові ознаки при взаємодії з відомими ознаками забезпечують появу нових технічних властивостей. Зокрема, шляхом введення нових операцій розроблено спосіб визначення потокозчеплень ротора й швидкості частотнорегульованого асинхронного двигуна. Це забезпечує усій заявленій сукупності ознак способу відповідність критерію «новизна». Аналоги, які містять ознаки, що відрізняються від прототипу, не знайдені, рішення явно не витікає з відомого рівня техніки. Виходячи з вищевикладеного, можна зробити висновок, що запропоноване рішення задовольняє критерію «винахідницький рівень». Ідея корисної моделі пояснюється кресленнями: на Фіг.1 – функціональна схема пристрою, що реалізує запропонований спосіб; 10 на Фіг.2 – функціональна схема пристрою, що реалізує запропонований спосіб при підвищеній точності визначення потокозчеплень ротора двигуна; на Фіг.3 і Фіг.4 – функціональні схеми варіантів реалізації датчика частоти; на Фіг.5 – функціональна схема пристрою, що реалізує запропонований спосіб при підвищеній точності визначення швидкості двигуна; на Фіг.6 і Фіг.7 – векторні діаграми, що пояснюють функціонування пристроїв, показаних на схемах на Фіг.2 і Фіг.3 відповідно. Функціональна схема пристрою на Фіг.1 містить блоки обчислювачів 1 і 2, обчислювачі швидкості 3 і оцінних значень потокозчеплень ротора 4, задатчик зворотного значення постійної часу ротора 5, датчики проекцій статорних напруг 6, 7 і статорних струмів 8, 9. Блоки обчислювачів 1 і 2 виконані між собою ідентично й містять кожний у своєму складі: регулятор 10 і інтегратор 11, два суматори 12 і 13, обчислювач проекції напруги ротора 14 і датчик проекції ЕРС ротора 15, що складається із суматора 16, пов'язаного своїм першим і другим входами відповідно через пропорційну ланку 17 і диференціююча ланка 18 з першим входом блоку обчислювачів 1 (або 2), а третій вхід суматора 16 є другим входом зазначеного блоку обчислювачів 1 (або 2). Причому вихід суматора 16 є виходом датчика проекції ЕРС ротора 15 і підключений до першого входу суматора 13 і першому входу обчислювача проекції напруги ротора 14, у якого другий вхід приєднаний до першого входу блоку обчислювачів 1 (або 2), а третій вхід і вихід обчислювача проекції напруги ротора 14 є відповідно третім входом і першим виходом зазначеного блоку обчислювачів 1 (або 2). При цьому вихід суматора 12 пов'язаний через регулятор 10 із другим входом суматора 13, вихід якого зв'язаний через інтегратор 11 з першим входом суматора 12, що є другим виходом блоку обчислювачів 1 (або 2), а другий вхід суматора 12 є четвертим входом зазначеного блоку обчислювачів 1 (або 2). Перший і другий входи блоків обчислювачів 1 і 2 підключені до виходів датчиків проекцій статорного струму 8, 9 і статорної напруги 6, 7 відповідно, треті входи блоків обчислювачів 1 і 2 з'єднані разом і підключені до виходу задатчика зворотного значення постійної часу ротора 5, а четверті входи блоків обчислювачів 1 і 2 приєднані відповідно до першого й другого виходів обчислювача оцінних значень потокозчеплень ротора 4. Перші виходи блоків обчислювачів 1 і 2 підключені відповідно до першого й другого входів обчислювача швидкості 3 і першому й другому входам обчислювача оцінних значень потокозчеплень ротора 4. Другі виходи зазначених блоків обчислювачів 1 і 2 приєднані відповідно до третього й четвертого входів обчислювача швидкості 3, вихід якого з'єднаний із третім входом обчислювача оцінних значень потокозчеплень ротора 4. У функціональній схемі пристрою на Фіг.2 (що реалізує запропонований спосіб при підвищеній точності визначення потокозчеплень ротора двигуна) блоки обчислювачів 1 і 2 виконані ідентично між собою й містять у своєму складі додатково 11 множний блок 19, підключений між виходом датчика проекцій ЕРС ротора 15 і першим входом суматора 13, причому другий вхід і вихід множного блоку 19 є відповідно п'ятим входом і третім виходом блоку обчислювачів 1 (або 2). При цьому згадані п'яті входи блоків обчислювачів 1 і 2 з'єднані разом і приєднані до виходу обчислювача корегувального коефіцієнта 20, що містить у своєму складі: перші й другий координатні перетворювачі 21 і 22, перший ділильний блок 23, фільтр 24, обчислювач оцінного значення ЕРС 25, датчик частоти 26 і обчислювач гармонійних функцій 27, що складається із других і третього ділильних блоків 28 і 29, квадраторного обчислювача 30 (що обчислює корінь квадратний із суми квадратів). Перші входи обчислювача 30 і ділильного блоку 28 з'єднані разом і підключені до виходу датчика проекції статорного струму 8, другий вхід обчислювача 30 і перший вхід ділильного блоку 29 з'єднані разом і підключені до виходу датчика проекції статорного струму 9, а другі входи ділильних блоків 28 і 29 з'єднані разом і підключені до виходу обчислювача 30. Перші входи координатних перетворювачів 21 і 22 з'єднані разом і підключені до виходу ділильного блоку 28, другі входи координатних перетворювачів 21 і 22 з'єднані разом і підключені до виходу ділильного блоку 29, а виходи першого 21 і другого 22 координатних перетворювачів приєднані відповідно до першого й другого входів ділильного блоку 23, підключеного своїм виходом до входу фільтра 24, вихід якого є виходом обчислювача корегувального коефіцієнта 20. Третій і четвертий входи координатного перетворювача 21 з'єднані з першим і другим виходами обчислювача оцінного значення ЕРС 25, у якого перший і другий входи підключені до других виходів блоків обчислювачів 1 і 2 відповідно, а третій вхід – з'єднаний з виходом датчика частоти 26. Третій і четвертий входи координатного перетворювача 22 приєднані до третіх виходів блоків обчислювачів 1 і 2 відповідно. Функціональна схема першого можливого варіанта реалізації датчика частоти 26 представлена на Фіг.3 і містить: суматор 31, пропорційноінтегральний регулятор 32, інтегратор 33, обчислювачі синуса 34 і косинуса 35, координатний перетворювач 36, перший і другий входи якого підключені до других виходів блоків обчислювачів 1 і 2 відповідно. При цьому вихід координатного перетворювача 36 пов'язаний через послідовно підключені суматор 31, регулятор 32 і інтегратор 33 із з'єднаними між собою разом входами обчислювачів 34 і 35, виходи яких підключені відповідно до третього й четвертого входів координатного перетворювача 36; причому, другий вхід суматора 31 з'єднаний із загальним виводом живлення, а вихід регулятора 32 є виходом датчика частоти 26. Функціональна схема другого можливого варіанта реалізації датчика частоти представлена на Фіг.4 і містить: множні блоки 37–40, суматори 41 і 41, ділильний блок 43. При цьому перші входи множних блоків 37 і 38 підключені до першим входом суматора 13 у блоках обчислювачів 1 і 2 відповідно, другий вхід множного блоку 37 підключе 39949 12 ний до з'єднаного разом першому й другому входам множного блоку 39 і до другого виходу блоку обчислювачів 1, другий вхід множного блоку 38 підключений до з'єднаного разом першому й другому входам множного блоку 40 і до другого виходу блоку обчислювачів 2. Виходи множних блоків 37 і 38 приєднані відповідно до першого й другого входів суматора 41, виходи множних блоків 39 і 40 приєднані відповідно до першого й другого входів суматора 42, а виходи суматорів 41 і 42 підключені відповідно до першого й другого входів ділильного блоку 43, вихід якого є виходом датчика частоти 26. У функціональній схемі пристрою на Фіг.5 (що реалізує запропонований спосіб при підвищеній точності визначення швидкості двигуна) задатчик зворотного значення постійної часу ротора 5 виконаний у вигляді координатних перетворювачів 44 і 45, обчислювача гармонійних функцій 46, блоків виділення модуля 47 і 48, інтеграторів 49 і 50, суматора 51 і пропорційної ланки 52, ділильного блоку 53, генератора імпульсів 54 і регістра 55. Обчислювач гармонійних функцій 46 складається з ділильних блоків 56 і 57, квадраторного обчислювача 58. Причому, перші входи ділильного блоку 56 і обчислювача 58 з'єднані разом і підключені до другого виходу блоку обчислювачів 1, перший вхід ділильного блоку 57 і другий вхід обчислювача 58 з'єднані разом і підключені до другого виходу блоку обчислювачів 2, другі входи ділильних блоків 56 і 57 з'єднані разом і підключені до виходу обчислювача 58 і до першого входу суматора 51, а виходи ділильних блоків 56 і 57 приєднані відповідно до перших і других входів координатних перетворювачів 44 і 45. Третій і четвертий входи координатного перетворювача 44 підключені до перших входів суматора 13 у блоках обчислювачів 1 і 2 відповідно, а вихід – зв'язаний через послідовно з'єднані між собою блок виділення модуля 47 і інтегратор 49 з першим входом ділильного блоку 53. Третій і четвертий входи координатного перетворювача 45 з'єднані з виходами датчиків проекцій статорного струму 8 і 9 відповідно, а вихід – зв'язаний через послідовно підключені між собою пропорційну ланку 52, суматор 51, блок виділення модуля 48 і інтегратор 50 із другим входом ділильного блоку 53, з'єднаного виходом із входом регістра 55. Вихід генератора імпульсів 54 підключений до з'єднаних разом другим (настановним) входам інтеграторів 49, 50 і регістра 55, а вихід регістра 55 є виходом задатчика зворотного значення постійної часу ротора 5. На векторній діаграмі на Фіг.6 (яка пояснює функціонування пристрою на Фіг.2) показані: нерухома «α–β» (пов'язана зі статором двигуна) і обертова «u–v» (пов'язана віссю «u» з узагальненим вектором статорного струму двигуна) ортогональні координатні системи; узагальнені вектори статорної напруги Us й статорного струму Is двигуна; d Is ) узаdt гальненого вектора ЕРС E ротора двигуна; оцінрозрахункові складові ( R s Is ) і ( L 13 не значення проекції Ev узагальненого вектора ЕРС ротора двигуна. На векторній діаграмі на Фіг.7 (яка пояснює функціонування пристрою на Фіг.2) показані: нерухома «α–β» (зв'язана зі статором двигуна) і обертова «x1–y1» (з аргументом θк дійсної осі «x1») ортогональні координатні системи; – узагальнений вектор потокозчеплення ротора; Ψy1 – проекція узагальненого вектора потокозчеплення ротора на вісь «y1» обертової координатної системи «x1–y1». Запропонований спосіб визначення потокозчеплень ротора й швидкості частотнорегульованого асинхронного двигуна функціонує (розглянемо на прикладі пристрою, показаного на Фіг.1) у такий спосіб. За допомогою датчиків статорної напруги 6, 7 і датчиків статорного струму 8, 9 контролюють проекції Usα, Isα і Usβ, Isβ узагальнених векторів відповідно статорної напруги Us й статорного струму Is на осі нерухомої ортогональної координатної системи «α–β» (пов'язаної віссю «α» с геометричною віссю статорної обмотки фази «А» двигуна). На виходах пропорційної 17 і диференціюючої 18 ланок, що входять до складу блоків обчислювачів 1 і 2, визначають проекції (на осі «α» і «β» нерухомої ортогональної координатної системи) падінь напруги ΔURα, ΔULα і ΔURβ, ΔULβ (від протікання статорних струмів) відповідно на активному опорі Rs статора й на сумарній індуктивності розсіювання Lσ двигуна: dI UR RsIs , UL L s , dt (15) dIs UR RsIs, UL L . dt За допомогою датчиків проекцій ЕРС ротора 15, що входять до складу блоків обчислювачів 1 і 2, розраховують проекції Eα, Eβ узагальненого вектора ЕРС ротора E двигуна на осі «α» і «β» нерухомої ортогональної координатної системи у вигляді діленої на коефіцієнт k зв'язку ротора різниці проекції Usα (або Usβ) узагальненого вектора статорної напруги Us на відповідну вісь даної координатної системи й двох від'ємників, перший з яких дорівнює добутку активного опору Rs статорної обмотки двигуна на значення проекції Isα (або Isβ) узагальненого вектора статорного струму Is на цю же вісь нерухомої ортогональної координатної системи, а другий – добутку сумарної індуктивності розсіювання Lσ двигуна на похідну за часом від тієї ж проекції Isα (або Isβ) узагальненого вектора статорного струму: dI E Us RsIs L s k , dt (16) . dIs E Us RsIs L k dt За допомогою обчислювачів проекції статорної напруги 14, що входять до складу блоків обчислювачів 1 і 2, розраховують проекції Uα, Uβ узагальненого вектора напруги ротора U на осі «α» і «β» 39949 14 нерухомої ортогональної координатної системи шляхом віднімання із проекцій Eα (або Eβ) узагальненого вектора ЕРС ротора добутків, обчислених у результаті множення проекцій Isα (або Isβ) узагальненого вектора статорного струму на коефіцієнт : U E Is , (17) . U E Is При цьому значення даного коефіцієнта у зазначеному обчислювачі 14 розраховують у вигляді добутку індуктивності намагнічування Lm двигуна на зворотне значення q його електромагнітної постійної часу (що надходить із задатчика даного значення 5): Lmq, де q 1 T . (18) Виходячи з відомих співвідношень для розрахунку електромагнітної постійної часу ротора T і коефіцієнта зв'язку k ротора [2]: T Lm Lr Rr , (19) , k Lm Lm Lr обчислене значення коефіцієнта дорівнює добутку коефіцієнта зв'язку ротора k на активний опір Rr ротора двигуна: k Rr , (20) де Lσr – індуктивність розсіювання ротора. З урахуванням останнього, залежності з (17) повністю рівнозначні співвідношенням (1), що використовуються у способі-прототипі для обчислення проекцій узагальненого вектора напруги ротора двигуна. Через визначені на виходах інтеграторів 11 (що входять у блоки обчислювачів 1 і 2) значення проекцій Ψα, Ψβ узагальненого вектора потокозчеплення ротора двигуна й розраховані проекції Uα, Uβ узагальненого вектора напруги ротора в обчислювачі 3 знаходять швидкість двигуна зі співвідношення: 2 2 U U . (21) В обчислювачі 4 через визначені значення швидкості ω і проекцій Uα, Uβ узагальненого вектора напруги ротора, через задане від обчислювача 5 зворотне значення q електромагнітної постійної часу ротора розраховують оцінні значення проек цій , узагальненого вектора потокозчеп лення ротора двигуна із залежностей: U qU 2 q2 , (22) , U qU 2 q2 ідентичних, з урахуванням (17), співвідношенням з (2). За допомогою суматорів 12 (що входять до складу блоків обчислювачів 1 і 2) контролюють відхилення ΔΨα, ΔΨβ між визначеними (на виходах інтеграторів 11) значеннями Ψα, Ψβ і оцінними значеннями , (отриманими на виходах об числювача 4) проекцій узагальненого вектора потокозчеплення ротора у вигляді: 15 39949 , . (23) Пропорційно даним відхиленням ΔΨα і ΔΨβ, що надходять на входи регуляторів 10 (що входять до складу блоків обчислювачів 1 і 2), на виході зазначених регуляторів (виконаних, наприклад, у вигляді пропорційних або пропорційноінтегральних ланок) формують керуючі сигнали Fα і Fβ. На виході суматорів 13 (що входять також до складу блоків обчислювачів 1 і 2) розраховуються різниці між проекціями Eα, Eβ узагальненого вектора ЕРС ротора й згаданих керуючих сигналів F α, F β : U E F , (24) . U E F При цьому за допомогою інтеграторів 11 (що входять до складу блоків обчислювачів 1 і 2) визначають шукані значення Ψα, Ψβ проекцій узагальненого вектора потокозчеплення ротора шляхом інтегрування за часом t отриманих з (24) різниць ΔUα і ΔUβ: t t U dt E F dt, 0 0 (25) . t t U dt E F dt 0 0 Запропонований спосіб, у порівнянні із прототипом, доповнений наступними простими операціями обчислення: віднімання й інтегрування, – які порівняно просто реалізуються сучасними цифровими обчислювачами. При цьому, шляхом здійснення в запропонованому способі безперервного контролю відхилень ΔΨα і ΔΨβ (між визначеними Ψα, Ψβ і оцінними , значеннями проекцій узагальненого вектора потокозчеплення ротора) і впливу (у функції цих відхилень) регуляторів 10 своїми вихідними сигналами Fα, Fβ на один із входів суматора 13, забезпечується ефективна компенсація часового дрейфу нуля інтеграторів 11 (що входять до складу блоків обчислювачів 1 і 2). У запропонованому способі (на відміну від способу-прототипу) здійснюється визначення проекцій потокозчеплення Ψα, Ψβ ротора й швидкості ω двигуна без застосування ітераційних (циклічних) розрахунків (на кожному часовому кроці розрахунку), що скорочує загальну кількість виконуваних обчислювальних операцій і зменшує час розрахунку. Це, у свою чергу, дозволяє знизити вимоги до обчислювача (застосовуваному в системі автоматичного керування) за обчислювальною потужністю та швидкодією, а, отже, – зменшити вартість зазначеного обчислювача й частотнорегульованого асинхронного електропривода в цілому. Пристрій на Фіг.2 (у якому реалізується запропонований спосіб при підвищеній точності визначення потокозчеплень ротора двигуна) функціонує аналогічно розглянутому пристрою на Фіг.1 з наступними відмінностями. Через проекції Isα, Isβ статорного струму двигуна, що поступають на його 16 входи з виходів датчиків 8 і 9, обчислювач гармонійних функцій 27 розраховує на своїх виходах значення косинуса й синуса від аргументу узагальненого вектора статорного струму двигуна шляхом ділення відповідно зазначених проекцій Isα, Isβ на корінь квадратний із суми квадратів цих проекцій: cos I Is I2 I2 , s s (26) , sin I Is I2 I2 s s які надходять на перший і другий входи координатних перетворювачів 21 і 22. На виході множних блоків 19 (що входять до складу блоків обчислювачів 1 і 2) контролюють * уточнені значення проекцій E* , E узагальненого вектора ЕРС ротора, які надходять на третій і четвертий входи координатного перетворювача 22. Даний координатний перетворювач 22 визначає уточнене значення проекції E* узагальненого v вектора ЕРС ротора двигуна на вісь «v» обертової ортогональної координатної системи «u–v», орієнтованою віссю «u» за узагальненим вектором статорного струму, у вигляді: * (27) E* E cos I E* sin I . v За допомогою датчика частоти 26 контролюють кутову частоту ωΨ узагальненого вектора потокозчеплення ротора двигуна. Через вказане значення кутової частоти ωΨ і значення проекцій Ψα, Ψβ узагальненого вектора потокозчеплення ротора, що поступають із других виходів блоків обчислювачів 1 і 2, за допомогою обчислювача 25 розраховують оцінні значення E , E проекцій узагальненого вектора ЕРС ротора двигуна на осі нерухомої ортогональної координатної системи «α–β»: E , (28) , E які надходять на третій і четвертий входи координатного перетворювача 21. Даний координатний перетворювач 21 обчислює на своєму виході оцінне значення Ev проекції узагальненого вектора ЕРС ротора двигуна на вісь «v» обертової ортогональної координатної системи «u–v» зі співвідношення: E E cos I E sin I . v (29) Ділильний блок 23 через сигнали Ev й E* , v що поступають на його входи з виходів координатних перетворювачів 21 і 22, розраховує частку від ділення уточненої E* й оцінної Ev проекцій узаv гальненого вектора ЕРС ротора на вісь «v» обертової ортогональної координатної системи «u–v» у вигляді: E* / Ev . Фільтр (низької частоти) 24 шляv хом виділення з вихідного сигналу блоку ділення 23 постійної складової визначає значення корегу 17 вального коефіцієнта ξ. Множні блоки 19 (що входять до складу блоків обчислювачів 1 і 2) обчислюють уточнені значення * проекцій E* , E узагальненого вектора ЕРС ро тора шляхом множення на корегувальний коефіцієнт ξ визначених проекцій Eα, Eβ цього вектора (що надходять із виходу датчика проекції ЕРС ротора 15 у блоках обчислювачів 1 і 2): E* E , (30) . * E E У тому випадку, якщо згадані уточнена E* й v оцінна Ev проекції рівні між собою, то, очевидно, значення корегувального коефіцієнта ξ дорівнює одиниці, і функціонування пристрою на Фіг.2 відбувається аналогічно описаному раніше пристрою, показаному на Фіг.1. Така ситуація виникає в тому випадку, якщо пропорційною ланкою 17 у датчику проекцій ЕРС ротора (що входить до складу блоків обчислювачів 1 і 2) задаються правильні (істинні) значення падінь напруги R * Is , R* Is на активs s ному опорі статорних обмоток двигуна: (31) R* Is RsIs та R* Is RsIs , s s де R* і Rs – відповідно заданий (пропорційs ною ланкою 17) і фактичний активні опори статора двигуна. Очевидно, у розглянутому випадку задане й фактичне значення активного опору статорної обмотки двигуна рівні: R* Rs . У результаті цього s на виходах датчиків ЕРС 15 і множних блоків 19 обчислюються істинні значення проекцій ЕРС ротора двигуна: * (32) E* E та E E , а на виході інтеграторів 11 – визначаються точні (істинні) значення проекцій Ψα, Ψβ потокозчеплень ротора двигуна. На практиці ж, внаслідок варіювання температурного режиму роботи двигуна (викликаного, наприклад, зміною його струмового завантаження або температури зовнішнього навколишнього середовища), спостерігається пов'язана із цим зміна фактичного значення Rs активного опору статорної обмотки двигуна, що призводить до нерівності заданого R* (у пропорційній ланці 17) і фактичноs го Rs активних опорів ( R* Rs ). У результаті цьоs го здійснюється неправильна (неповна) компенсація пропорційною ланкою 17 (у блоках обчислювачів 1 і 2) падінь напруг на активному опорі статорної обмотки двигуна: (33) R* Is RsIs та R* Is RsIs , s s що, у свою чергу, призводить у пристрої на Фіг.1 до помилки у визначенні проекцій Eα, Eβ узагальненого вектора ЕРС ротора, і, як наслідок, – до помилки при визначенні потокозчеплень ротора 39949 18 Ψα, Ψβ на виході інтеграторів 11 у блоках обчислювачів 1 і 2. У пристрої на Фіг.2 при даній ситуації виникає відхилення (відмінність) між оцінним Ev (що розраховується координатним перетворювачем 21 з (28) і (29) через проекції Ψα, Ψβ узагальненого вектора потокозчеплення ротора й кутову частоту ωΨ) і уточненим E* (що обчислюють на виході коорv динатного перетворювача 22) значеннями проекцій узагальненого вектора ЕРС ротора двигуна на вісь «v» обертової ортогональної координатної системи «u–v» (орієнтованої віссю «u» за узагальненим вектором статорного струму двигуна). При цьому, відповідно до векторної діаграми на Фіг.6, проекція на згадану вісь «v» узагальненого вектора ЕРС ротора E не залежить від падіння напруги ( R s Is ) на активному опорі статорної обмотки двигуна, а, отже, – і від значення Rs активного опору статора двигуна. При виникненні зазначених відхилень між уточненим E* (не залежним від активного опору стаv тора Rs) і оцінним Ev значеннями проекцій узагальненого вектора ЕРС ротора стає відмінним від одиниці значення корегувального коефіцієнта ξ, що розраховується на виході обчислювача 20. За допомогою даного корегувального коефіцієнта * знаходяться із (30) нові уточнені значення E* , E проекцій узагальненого вектора ЕРС ротора двигуна, які забезпечують рівність між собою уточненого E* й оцінного Ev значень проекцій узагальv неного вектора ЕРС ротора на вісь «v» обертової ортогональної координатної системи «u–v»: (34) E* E . v v При цьому, очевидно, при виконанні умови * (34) у визначених уточнених значеннях E* , E проекцій узагальненого вектора ЕРС ротора (на осі нерухомої ортогональної координатної системи «α–β») здійснюється повною мірою компенсація падінь напруг (RsIsα) і (RsIsβ) на активному опорі Rs статорної обмотки двигуна. За рахунок цього, у свою чергу, забезпечується уточнене визначення проекцій Ψα, Ψβ узагальненого вектора потокозчеплення ротора на виході інтеграторів 11 у блоках обчислювачів 1 і 2 при температурному дрейфі активного опору Rs статорної обмотки двигуна. Варіант реалізації датчика частоти 26, показаний на Фіг.3, функціонує в такий спосіб. На виході інтегруючої ланки 33 формується сигнал аргументу θк дійсної осі «x1» обертової ортогональної координатної системи «x1–y1». Через зазначений сигнал аргументу θк на виході обчислювачів 34 і 35 обчислюються гармонійні функції: sin θк і cos θк відповідно. На виході координатного перетворювача 36 через сигнали проекцій Ψα, Ψβ узагальненого вектора потокозчеплення ротора, що поступають на його входи із других виходів блоків обчислювачів 1 і 2, і згадані сигнали гармонійних функцій cos θк, sin θк розраховується проекція Ψу1 19 39949 узагальненого вектора потокозчеплення ротора на вісь «y1» обертової ортогональної координатної системи «x1–y1» зі співвідношення: y1 cos к sin к . (35) З виходу суматора 31 на вхід пропорційноінтегрального регулятора 32 надходить відхилення між заданим (яке задається рівним нулю) і розрахованим з (35) значенням проекції Ψу1 узагальненого вектора потокозчеплення. Швидкодіючий регулятор 32 впливає своїм вихідним сигналом ωк на вхід інтегральної ланки 33 таким чином, щоб на вході цього регулятора підтримувався сигнал близьким до нуля: y1 0 . (36) Відповідно до векторної діаграми на Фіг.7 це означає, що опиняються сполученими вісь «x1» і «y1» координатної системи «x1–y1» відповідно з віссю «x» і «y» обертової ортогональної координатної системи «x–y», зв'язаною віссю «x» з узагальненим вектором потокозчеплення ротора двигуна. У цьому випадку, очевидно, аргументи θк і θΨ дійсної осі «x1» координатної системи «x1–y1» і узагальненого вектора потокозчеплення ротора рівні між собою: к , (37) а, отже, рівні і їхні похідні: d d к к , (38) dt dt що представляють собою кутові частоти обертання координатної системи «x1–y1» і узагальненого вектора потокозчеплення ротора двигуна відповідно. Беручи до уваги інтегральну передавальну функцію ланки 33, на його вході, очевидно, формується сигнал, що дорівнює кутовій частоті обертання узагальненого вектора потокозчеплення ротора: к , (39) який є вихідним сигналом датчика 26 у пристрої на Фіг.4. Інший варіант реалізації датчика частоти 26, наведений на Фіг.4, функціонує в такий спосіб. * Через проекції E (або E* ), E (або E ) уза гальненого вектора ЕРС ротора (що поступають з перших входів суматорів 13 і із других виходів блоків обчислювачів 1 і 2) та проекції Ψα, Ψβ узагальненого вектора потокозчеплення ротора двигуна на виході множних блоків 37 і 38 розраховуються добутки: ΨαEβ і ΨβEα, а на виході суматора 41 – вираз (ΨαEβ – ΨβEα), що дорівнює різниці вказаних добутків. При цьому на виході множних блоків 39 і 40 розраховуються квадрати проекцій уза2 гальненого вектора потокозчеплення ротора: і 2 відповідно, а на виході суматора 42 – сума 2 2 ( ) зазначених квадратів проекцій. З урахуванням вищевикладеного на виході ділильного блоку 43 обчислюється кутова частота ωΨ уза 20 гальненого вектора потокозчеплення ротора у вигляді [2]: 2 2 E E . (40) Пристрій на Фіг.5 (у якому реалізується запропонований спосіб при підвищеній точності визначення швидкості двигуна) функціонує аналогічно розглянутому пристрою на Фіг.1 з наступною відмінністю. На входи обчислювача гармонійних функцій 46 надходять із других виходів блоків обчислювачів 1 і 2 проекції Ψα, Ψβ узагальненого вектора потокозчеплення ротора двигуна. За допомогою обчислювача 58 розраховують модуль Ψ узагальненого вектора потокозчеплення ротора у вигляді кореня квадратного із суми квадратів певних проекцій Ψα, Ψβ цього вектора на осі «α» і «β» нерухомої ортогональної координатної системи: 2 2 . (41) За допомогою множних блоків 56 і 57 розраховують значення косинуса й синуса від аргументу θΨ узагальненого вектора потокозчеплення ротора шляхом ділення відповідно проекцій Ψα і Ψβ на модуль узагальненого вектора потокозчеплення ротора: cos , (42) . sin Розраховані значення зазначених гармонійних функцій cos θΨ і sin θΨ надходять на перший й другий входи координатних перетворювачів 44 і 45. На третій і четвертий входи координатного перетворювача 44 надходять проекції E (або E* ), E * (або E ) узагальненого вектора ЕРС ротора з першого входу суматора 13. На третій і четвертий входи координатного перетворювача 45 надходять проекції Isα, Isβ узагальненого вектора статорного струму з датчиків струму 8 і 9 відповідно. За допомогою координатних перетворювачів 44 і 45 визначають відповідно проекцію Ex узагальненого вектора ЕРС ротора й проекцію Isx узагальненого вектора статорного струму двигуна на вісь «x» обертової ортогональної координатної системи «x–y», орієнтованої віссю «x» за узагальненим вектором потокозчеплення ротора двигуна, у вигляді: E x E cos E sin , (43) . Isx Is cos Is sin На виході пропорційної ланки 52 обчислюють добуток: (LmIsx), а на виході суматора 51 – вираз: (Ψ – LmIsx), де Lm – індуктивність намагнічування двигуна. За допомогою блоків виділення модуля 47 і 48 визначають абсолютні значення від вищезгаданих добутків й вираз у вигляді: | LmIsx | і | Ψ – LmIsx | відповідно. За допомогою інтеграторів 49 і 50 розраховують інтеграли И1, И2 за часом за однаковий часовий інтервал (наприклад, рівний 10–20 мс) від абсолютного значення проекції Ex узагальненого 21 39949 вектора ЕРС ротора й від абсолютного значення різниці між модулем Ψ узагальненого вектора потокозчеплення ротора й добутком індуктивності Lm намагнічування двигуна на проекцію Isx узагальненого вектора статорного струму: . 0 И2 LmIsx dt 0 И1 Ex dt, (44) За допомогою ділильного блоку 53 розраховують частку від ділення зазначених інтегралів у вигляді: И1 / И2, – яка надходить на вхід регістра 55. При цьому на настановні входи регістра 55, інтеграторів 49 і 50 надходять вузькі прямокутні імпульси (з періодом ) від генератора імпульсів 54, із приходом яких відбувається періодичне обнулення вихідних сигналів інтеграторів 49, 50 і передача сигналу, рівного И1 / И2, із входу регістра 55 на його вихід. У такий спосіб із приходом кожного чергового імпульсу від генератора 54 на виході задатчика 5 встановлюється нове зворотне значення q електромагнітної постійної часу ротора. Це нове значення залишається незмінним протягом періоду генератора імпульсів 54 і дорівнює частці від ділення інтегралів з (44): q И1 И2 . (45) При цьому відомо, що внаслідок зміни температурного режиму двигуна також відбувається зміна активного опору Rr ротора двигуна, що призводить, як випливає з (19), до варіювання значення електромагнітної постійної часу T ротора двигуна. Це, у свою чергу, має вплив на точність розрахунку зі співвідношення (21) швидкості двигуна, оскільки вхідні в це співвідношення проекції Uα, Uβ узагальненого вектора напруги ротора залежать, згідно (17) і (18), від зворотного значення q електромагнітної постійної часу ротора двигуна. Для короткозамкненого асинхронного двигуна відомі співвідношення [2]: d LmIsx T , dt (46) , d Ex dt з яких стає можливим визначення зворотного значення q електромагнітної постійної часу ротора у вигляді: 1 Ex . q (47) T LmIsx Для виключення в останньому співвідношенні виконання обчислень за різнойменних можливих знаках значень, що містяться у чисельнику й зна 22 меннику, а також – для виключення можливого ділення на близькі до нуля значення в знаменнику, у запропонованому способі розрахунковий вираз (47) замінено еквівалентними йому співвідношеннями (44) і (45), у яких зворотне значення q електромагнітної постійної часу ротора визначається у вигляді частки від ділення часових інтегралів (за період ), узятих від абсолютних значень виразів: | Ψ – LmIsx | і | Ex |. З урахуванням цього в пристрої на Фіг.5 за допомогою задатчика 5 періодично (з періодом, що дорівнює ) визначають уточнені зворотні значення q електромагнітної постійної часу ротора двигуна, які надходять на входи обчислювачів проекцій напруги ротора 14 (у блоках обчислювачів 1 і 2), а також – на вхід обчислювача оцінних значень проекцій потокозчеплення ротора 4. Як наслідок, обчислювачі 14 і 4 визначають уточнені (враховуючі температурні зміни постійної часу ротора двигуна) значення проекцій Uα, Uβ узагальненого вектора напруги ротора зі співвідношень (17), (18) і оцінні значення , проекцій узагальненого вектора потокозчеплення ротора із залежностей (22). Це, у свою чергу, дозволяє (за рахунок використання зазначених уточнених значень) обчислювачу 3 визначати більш точно зі співвідношення (21) поточну швидкість ω двигуна. Уточнене визначення за допомогою запропонованого способу потокозчеплень ротора та швидкості двигуна дозволяє підвищити швидкодію та поліпшити якість регулювання електромеханічних процесів частотно-регульованих асинхронних електроприводів, що створюються на базі різних типів статичних перетворювачів частоти (інверторів напруги та струму, безпосередніх перетворювачів частоти) з широтно-імпульсною модуляцією. Виходячи з вищевикладеного можна зробити висновок, що запропоноване рішення задовольняє критерію «Промислова придатність». Джерела інформації: 1. Современное состояние и тенденции в асинхронном частотно-регулируемом электроприводе (краткий аналитический обзор) /Л.Х. Дацковский, В.И. Роговой, Б.И. Абрамов и др. – Электротехника. – 1996. – №10. – С.22. 2. Волков А.В. Идентификация потокосцепления ротора частотно-регулируемого асинхронного двигателя // Электротехника. – 2002. – №6. – С.4046. 3. Шрейнер Р.Т., Дмитренко Ю.А. Оптимальное частотное управление асинхронными электроприводами. – Кишинев: Штиинца, 1982. – 224с. 23 39949 24 25 39949 26 27 39949 28 29 39949 30 31 Комп’ютерна верстка Г. Паяльніков 39949 Підписне 32 Тираж 28 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determination of rotor flux linkage and speed of frequency - controlled asynchronous motor
Автори англійськоюVolkov Oleksandr Vasyliovych, Skalko Yurii Serhiiovych
Назва патенту російськоюСпособ определения потокосцеплений ротора и скорости частотно-регулируемого асинхронного двигателя
Автори російськоюВолков Александр Васильевич, Скалько Юрий Сергеевич
МПК / Мітки
МПК: H02P 21/00
Мітки: потокозчеплень, ротора, двигуна, спосіб, частотно-регульованого, швидкості, визначення, асинхронного
Код посилання
<a href="https://ua.patents.su/16-39949-sposib-viznachennya-potokozcheplen-rotora-jj-shvidkosti-chastotno-regulovanogo-asinkhronnogo-dviguna.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення потокозчеплень ротора й швидкості частотно-регульованого асинхронного двигуна</a>
Попередній патент: Спосіб оцінки стану підшлункової залози при механічних пошкодженнях
Наступний патент: Розпилювальна сушильна установка
Випадковий патент: Пристрій для піднесення чисел до довільного степеня за модулем три модулярної системи числення












