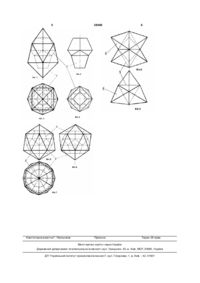
Навчальна модель багатогранників (тіла лося)

1. Навчальна модель багатогранників, в якій вихідним є тетраедр і застосовані правильні піраміди та антипризми з гранями у вигляді рівносторонніх трикутників і/або рівнобедрених трикутників, яка відрізняється тим, що піраміди, що мають однакові основи з антипризмами, з'єднані між собою по цих основах в єдиний багатогранник, причому пірамід обов'язково дві, а між ними одна антипризма; багатогранники розташовані в безкінечний ряд по єдиному алгоритму: 4=4:1 (тетраедр) = 8:2 (октаедр) = 12:3 (додекаедр) =16:4 (новий напівправильний багатогранник) = 20:5 (ікосаедр) = 24:6 (новий багатогранник ) = 28:7 (новий багатогранник) Þ ∞, в чисельнику позначена кількість граней, в знаменнику - місце багатогранника в ряду натурального ряду чисел; частка для всіх членів ряду дорівнює 4. 2. Навчальна модель за п. 1, яка відрізняється тим, що при з'єднанні двох однакових правильних 3 38968 4 ній справі [наприклад, а.с.1637783, 1991, Бюл. дві нескінченності: "в ширину" - нескінченність ба№12, де фігур ує октаедр і ромбододекаедр] тощо. гатогранників по кількості граней; "в глибину" - неНайближчим аналогом заявленій корисній москінченність багатогранників по кількості антиделі є багатогранники, описані в вищезазначеній призм в багатограннику. книзі [1], де найбільш повно розглянуті відомі гео4. При з’єднанні правильних пірамід своїми метричні багатогранники. Вивчення вищезазначеосновами, тобто при утворенні біпірамід, отримуєних джерел та інших, які не приведені з метою мо нескінченний ряд з новим алгоритмом, в якому компактності опису, може свідчити, що заявлена в чисельнику позначена кількість бокових граней модель багатогранників є новою і аналітично біпіраміди, а в знаменнику – зростаюча арифметипредставлена новим математичним виразом, що чна прогресія з різницею 0,5, частка для всіх біпівідповідає п.10.2.3 Правил складання заявки. рамід дорівнює 4. Найближчий аналог якби підводить риску під 5. Розвиток геометричних фігур часто пов'язапошуком нових напівправильних багатогранників і ний з розширенням такої їх властивості як симетце його недолік. Адже неможливість отримання ричність. В запропонованих багатогранниках це нових напівправильних багатогранників повинна найбільш проявилось в зірчастих біпірамідах, які бути строго математично доведена. Ефективність утворюються при доповненні вказаних правильних навчального процесу зросте, якщо в вивчення вібіпірамід однаковими трикутними пірамідами так, домих багатогранників ввести раніше невідомі щоб їх основи були конгруентні граням біпірамід і багатогранники, об'єднані в певний ряд алгоритлежали на цих гранях, створивши зірчасті багатомом у вигляді відповідного математичного виразу. гранники з центральною і площинною симетрією. Розгляд найближчого аналога та інших джеВказана новизна (і графічна, і аналітична) зарел свідчить, що запропонована нова модель баявлених тіл та їх рядів має високий навчальний гатогранників, особливості якої в наступному: ефект, сприяючи розвитку у молоді інтересу і впе1. Ці фігури є напівправильними багатограннивненості, що активна дослідницька діяльність обоками та являють собою суму (композицію) двох в'язково приведе до успіху: вважалось, що по баправильних однакових пірамід і антипризми між гатогранникам все зроблено, але пошуки привели ними, основи пірамід і анти-призм конгруентні до нового ряду напівправильних багатогранників, (тобто повністю однакові) та з'єднані для отриманпричому маючих прикладне значення. Запропононя єдино фігури. ваною корисною моделлю показано, як можна на2. Заявлені багатогранники становлять нескінвчати недорогими та складними технічними засоченний ряд і мають новий спільний алгоритм побами, а винайти та зобразити графічно і будови цього ряду, а саме: починаючи з відомих аналітично нові геометричні тіла. правильних багатогранників (тіл Платона) маємо Перелік фігур і пояснення зображень. відношення у те траедра чотирьох його граней до Заявлені багатогранники зображені на відповіодиниці, другим членом ряду приймаємо октаедр, дних ортогональних проекціях фігур з наступними у нього 8 граней і друге місце в ряду (8:2=4), тобто позначеннями фігур і елементів фігур цифрами: відношення теж дорівнює чотирьом, далі йде доФіг.1, 2 - дві проекції напівправильного 16декаедр (12 граней і третє місце в ряду, 12:3=4), гранника І (види спереду і зверху); далі йде новий напівправильний багатогранник Фіг.3, 4 - дві проекції напівправильного 18гексадекаедр, тобто 16-гранник (входить в тіла гранника 2, він двоїстий 16-граннику; Лося), у якого всі грані однакові рівносторонні трина Фіг.5, 6 7 дані три проекції напівправильнокутники і відношення 16:4=4, далі йде ікосаедр (20го 24-гранника 3 разом з двоїстим йому багатограннйк – тіло Платона, відношення 20:5=4), на гранником 4, що показаний штриховими лініями; шостому місці новий напівправильний багатогранна Фіг.8, 9 зображений в двох проекціях зірчаник, являючий собою 24-гранник (24:6=4), відкристий бітетраедр 5, позицією 6 позначені добудоваваючий ряд нових багатогранників (тіл Лося) з одні на гранях бітетраедра правильні трикутні піранаковим відношенням кількості граней до місця в міди. Для компактності заявки кількість графічних ряду, дорівнюючим 4, тобто 28-гранник 28:7=4, 32зображень мінімальна. гранник 32:8=4 і далі – теоретично до нескінченноВідомості, які підтверджують і розкривають сті. Починаючи з 24-гранника, у кожного багатоможливість здійснення. гранника грані є однаковими рівнобедреними триПрийоми виготовлення моделей багатогранкутниками, відношення кількості граней до місця в ників, описані в [1], придатні також для заявлених ряду є число "4" і різниця між кількістю граней у нових моделей, тобто можливо ефективно замінисусідніх членів ряду є також число "4". ти навчальні моделі типу вище приведених, на3. Теоретично правильних антипризм, як і праприклад, по авторському свідоцтву 1656575 або вильних пірамід, може бути нескінченна кількість, 1339621, які дорого коштують і тому рідко застосозгідно заявки вони повинні мати конгруентні основуються, запропонованою корисною моделлю. ви та з'єднуватись цими основами; ми маємо тут 5 Комп’ютерна в ерстка Г. Паяльніков 38968 6 Підписне Тираж 28 прим. Міністерство осв іт и і науки України Держав ний департамент інтелектуальної в ласності, вул. Урицького, 45, м. Київ , МСП, 03680, Україна ДП “Український інститут промислов ої в ласності”, вул. Глазунова, 1, м. Київ – 42, 01601