Аналізатор спектра фур’є та хартлі

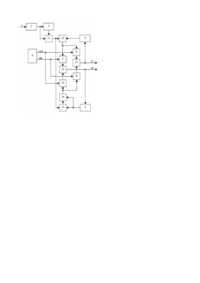
Винахід належить до галузі цифрової обчислювальної техніки і може бути застосований у пристроях динамічного спектрального аналізу в реальному масштабі часу. Відомий аналізатор спектра Фур'є для динамічного спектрального аналізу, що реалізує рекурентний метод обчислення перетворення Фур'є на ковзних інтервалах [Патент США №3778606, кл. 235-156, 1973], котрий містить аналого-цифровий перетворювач, три блоки пам'яті, блок формування синусних та косинусних вагових коефіцієнтів, чотири помножувачі та чотири суматори. Недоліком даного пристрою є залежність обчислюваного перетворення від положення вибірки відліків вхідної послідовності відносно початку відліку та низькі функціональні можливості, обмежені визначенням лише спектра Фур'є. Найбільш близьким за технічною сутністю до запропонованого є аналізатор спектра Фур'є для динамічного спектрального аналізу, що реалізує рекурентний метод обчислення перетворення Фур'є на ковзних інтервалах [А. с. СССР, №560232, кл. G06F15/34, 1977], який містить аналого-цифровий перетворювач, з першого по третій блоки пам'яті, блок формування синусних та косинусних вагових коефіцієнтів, з першого по четвертий помножувачі, з першого по четвертий суматори, вхід аналого-цифрового перетворювача є входом пристрою, а вихід з'єднаний з першим входом першого суматора та входом першого блока пам'яті, вихід якого з'єднаний з другим входом першого суматора, вихід якого з'єднаний з першим входом другого суматора, другий вхід якого з'єднаний з виходом другого блока пам'яті, перший вихід блока формування синусних та косинусних вагових коефіцієнтів з'єднаний з першими входами першого та другого помножувачів, а другий вихід з'єднаний з першими входами третього та четвертого помножувачів, другі входи першого та третього помножувачів з'єднані з виходом другого суматора, а другі входи другого та четвертого помножувачів з'єднані між собою, виходи другого та третього, першого та четвертого помножувачів з'єднані з першими та другими входами відповідно третього та четвертого суматорів, виходи яких з'єднані з входами другого та третього блоків пам'яті та є першим та другим виходами пристрою відповідно. Недоліком даного пристрою є низькі функціональні можливості, обмежені визначенням лише спектра Фур'є. В основу винаходу поставлено задачу створення аналізатора спектра Фур'є та Хартлі, що реалізує рекурентні методи обчислення перетворень Фур'є та Хартлі на ковзних інтервалах, в якому за рахунок введення нових блоків та зв'язків досягається визначення динамічних спектрів Фур'є або Хартлі, внаслідок чого розширюються функціональні можливості аналізатора. Поставлена задача досягається за рахунок того, що в аналізатор спектра Фур'є та Хартлі, що містить аналого-цифровий перетворювач, з першого по третій блоки пам'яті, блок формування синусних та косинусних вагових коефіцієнтів, з першого по четвертий помножувачі, з першого по четвертий суматори, вхід аналогоцифрового перетворювача є входом пристрою, а вихід з'єднаний з першим входом першого суматора та входом першого блока пам'яті, вихід якого з'єднаний з другим входом першого суматора, вихід якого з'єднаний з першим входом другого суматора, другий вхід якого з'єднаний з виходом другого блока пам'яті, перший вихід блока формування синусних та косинусних вагових коефіцієнтів з'єднаний з першими входами першого та другого помножувачів, а другий вихід з'єднаний з першими входами третього та четвертого помножувачів, другі входи першого та третього помножувачів з'єднані з виходом другого суматора, а другі входи другого та четвертого помножувачів з'єднані між собою, виходи другого та третього, першого та четвертого помножувачів з'єднані з першими та другими входами відповідно третього та четвертого суматорів, виходи яких з'єднані з входами другого та третього блоків пам'яті та є першим та другим виходами пристрою відповідно, введені комутатор та п'ятий суматор, перший вхід якого з'єднаний з виходом першого суматора, а другий вхід з'єднаний з виходом третього блока пам'яті та першим входом комутатора, другий вхід якого з'єднаний з виходом п'ятого суматора, а вихід з'єднаний з другим входом другого помножувача. Введення в аналізатор комутатора та п'ятого суматора разом з їх зв'язками дозволило реалізувати рекурентні методи обчислення перетворень Фур'є та Хартлі на ковзних інтервалах, внаслідок чого стало можливим визначення динамічних спектрів Фур'є або Хартлі, що розширило функціональні можливості аналізатора. На кресленні представлена блок-схема пристрою аналізатора спектра Фур'є та Хартлі. Пристрій містить вхід 1, аналого-цифровий перетворювач 2, блоки 3-5 пам'яті, блок 6 формування синусних та косинусних вагових коефіцієнтів, помножувачі 7-10, суматори 11-15, комутатор 16, виходи 17-18. Вхід аналого-цифрового перетворювача 2 є входом 1 пристрою, а вихід з'єднаний з першим входом першого суматора 11 та входом першого блока З пам'яті, вихід якого з'єднаний з другим входом першого суматора 11, вихід якого з'єднаний з першими входами п'ятого 15 та другого 12 суматора, другий вхід якого з'єднаний з виходом другого блока 4 пам'яті. Синусний вихід блока 6 формування синусних та косинусних вагових коефіцієнтів з'єднаний з першими входами першого 7 та другого 8 помножувачів, а косинусний вихід з'єднаний з першими входами третього 9 та четвертого 10 помножувачів. Другі входи першого 7 та третього 9 помножувачів з'єднані з виходом другого суматора 12, а другі входи другого 8 та четвертого 10 помножувачів з'єднані з виходом комутатора 16. Виходи другого 8 та третього 9, першого 7 та четвертого 10 помножувачів з'єднані з першими та другими входами відповідно третього 13 та четвертого 14 суматорів, виходи яких з'єднані з входами другого 4 та третього 5 блоків пам'яті та є першим 17 та другим 18 виходами пристрою відповідно. Вихід третього блока пам'яті 5 з'єднаний з другим входом п'ятого суматора 15 та першим входом комутатора 16, другий вхід якого з'єднаний з виходом п'ятого суматора 15. Пристрій працює наступним чином. Рекурентні методи обчислення перетворень Фур'є та Хартлі дійсних послідовностей на ковзних інтервалах, коли значення перетворень оновлюються з надходженням кожного нового значення відліку вхідної послідовності, базуються на основі математичних виразів (1) та (2) відповідно: j2 pk Fi+1(k ) = [Fi (k ) +[x(N + i) - x(i)]]e N (1) Hi +1(k ) = [Hi (k ) + [x(N + i) - x(i )]]cos 2 pk N (2) 2 pk - [Hi (N - k ) + [x(N + i) - x(i)]]sin N Fi+1(k ) Fi (k ) - комплексні дискретні значення перетворення Фур'є вхідної послідовності розміром N на , де (i + 1) - му та і - му інтервалах відповідно (k = 0, N / 2 - 1 - номер значення перетворення; i = 0,1,2 ...) ; Hi+1( k ) Hi (k ) - дійсні дискретні значення перетворення Хартлі вхідної послідовності розміром N на (i + 1) - му , та і - му інтервалах відповідно; x(N + i) та x( i) - значення відліків вхідної послідовності. Обчислення виразів (1) та (2) в пристрої виконується шляхом обчислення виразів (3) та (4) відповідно: 2pk ü Re Fi +1(k ) = [Re Fi (k ) + [x(N + i) - x(i )]]cos N ï ï 2pk ï - [ImFi (k )]sin ï ï N ý (3) 2 pk ï Im Fi+1( k ) = [Re Fi ( k ) + [x (N + i ) + x(i)]]sin + ï N ï 2 pk ï + [ImFi ( k )]cos ï N þ 2pk N ü -ï ï 2pk ï - [Hi (N - k ) + [x(N + i) - x(i )]]sin ï ï N ý 2pk ï Hi +1(k ) = [Hi (k ) + [x (N + i) - x( i)]]sin + ï N ï 2 pk ï + [Hi (N - k ) + [x (N + i ) - x (i)]]cos ï N þ Hi +1(k ) = [Hi (k ) + [x (N + i) - x( i)]]cos (4) де Re та Im - дійсні та уявні частини значень перетворення Фур'є. Пристрій працює циклічно. Початок кожного циклу визначається надходженням на вхід блока 3 пам'яті нового дискретного значення послідовності відліків, котра формується за допомогою аналого-цифрового перетворювача 2, на вхід якого з входу 1 пристрою подається досліджуваний аналоговий сигнал. На початку кожного циклу в блоці 3 пам'яті зберігаються N значень відліків і - го інтервалу вхідної послідовності, а в блоках 4-5 пам'яті F (k ) перетворення Фур'є при визначенні спектра Фур'є відповідно дійсні та уявні частини комплексних значень i Hi (N - k ) Hi (k ) та перетворення Хартлі при визначенні спектра Хартлі на і - му інтервалі. В або дійсні значення початковому стані (i = 0 ) комірки всіх блоків 3-5 пам'яті обнулені. Режим роботи пристрою визначається комутатором 16: при комутації на вихід значень з входу, підключеного до виходу блока 5 пам'яті, визначається спектр Фур'є, з входу, підключеного до виходу суматора 15, - спектр Хартлі. На початку циклу значення нового відліку вхідної послідовності зберігається в блоці 3 пам'яті та надходить на перший вхід суматора 11, на другий вхід якого з блоку 3 пам'яті надходить значення відліку вхідної послідовності, що передувало новому відліку на N відліків, в результаті чого на виході суматора 11 формується значення [x(N + i) - x(i)] , котре надходить на перші входи суматорів 12 та 15 і міститься на них на протязі визначення значень перетворення Фур'є або Хартлі на (i + 1) - му інтервалі. Кожен цикл складається з N / 2 підциклів визначення значень перетворення Фур'є або Хартлі (k = 0, N / 2 - 1) . На початку кожного підциклу на виходах блоків 4-5 пам'яті з'являються значення дійсної та уявної частини H (N - k ) H (k ) F (k ) та i перетворення Хартлі при перетворення Фур'є або дійсні значення i комплексного значення i визначенні спектра Фур'є або Хартлі відповідно, а на виходах блока 6 формування синусних та косинусних 2pk 2 pk cos N та N відповідно. вагових коефіцієнтів - значення [Re Fi (k) + [x(N + i) - x(i)]] або [Hi(k ) + [x(N + i) - x(i )]] при визначенні [H (N - k) + [x(N + i) - x(i )]] при спектра Фур'є або Хартлі відповідно, а на виході суматора 15 визначається значення i На виході суматора 12 формуються значення визначенні спектра Хартлі. На виходах помножувачів 9 та 7 формуються значення перших добутків, а на виходах помножувачів 8 та 10 - значення других добутків виразів (3) або (4) при визначенні спектра Фур'є або Хартлі відповідно. Кінцеві значення виразів (3) або (4) при визначенні спектра Фур'є або Хартлі відповідно формуються на виходах суматорів 13 та 14, зберігаються в блоках 4 та 5 пам'яті й поступають на виходи 17 та 18 пристрою відповідно.