Наочний посібник з математики

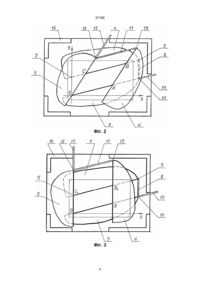
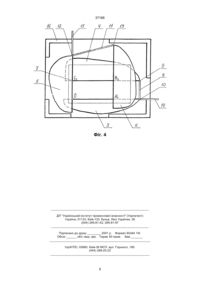
1. Наочний посібник з математики, який містить передню панель із прозорого матеріалу з нанесеною на її поверхні декартовою системою координат, паралельну їй задню панель, прокладки, що фіксують відстань між панелями, стержні і шарніри, який відрізняється тим, що посібник містить набір пластин, виконаних у формі півплощин, які утворюють своїми прямими межами вікно-паралелограм, пластини змонтовані між панелями із можливістю плоскопаралельних переміщень, які зберігають інваріантними форму і площу вікнапаралелограма, пластини шарнірно закріплені на задній панелі і попарно з'єднані стержнями так, що вузли кріплення і з'єднання кожної пари є вершинами двох незалежних шарнірних паралелограмів, A (54) НАОЧНИЙ ПОСІБНИК З МАТЕМАТИКИ 37168 ри, які складаються із жорстко зв'язаних з валами втулок і розміщених одне в одному кілець, зовнішнє з яких взаємодіє із тяговими елементами [2. А.с. СССР № 1494030, МКИ4 G 09 В 23/08, 1989 г. прототип]. Недоліком пристрою є те, що площа шарнірного паралелограма не має властивості інваріантності, а тому він не може бути моделлю визначника другого порядку. В основу винаходу поставлена задача вдосконалення наочного посібника за рахунок конструктивного виконання його елементів, що сприяє поліпшенню процесу сприйняття математичних понять шляхом ілюстрації геометричного змісту визначника другого порядку. Поставлена задача досягається шляхом того, що наочний посібник містить передню панель із прозорого матеріалу із нанесеною на її поверхні декартовою системою координат, паралельну їй задню панель і прокладки, які фіксують відстань між ними. За допомогою стержнів і шарнірів між панелями змонтовані, із можливістю плоскопаралельних переміщень, чотири пластини у формі півплощин, які своїми прямими межами утворюють рухоме вікно у вигляді паралелограма із незмінною площею; пластини закріплені на задній панелі і попарно з'єднані стержнями так, що вузли кріплення і з'єднання кожної пари є вершинами двох незалежних шарнірних паралелограмів; дві суміжні пластини, що утворюють гострий кут вікнапаралелограма, із можливістю повороту у вершині цього кута, закріплені на задній панелі в точці, яка відповідає початку координат, а дві інші пластини із можливістю повороту - закріплені на задній панелі, відповідно, одна - в точці перетину її прямої межі із віссю ординат, друга - у вершині тупого кута вікна-паралелограма; кожна пара пластин оснащена поворотним важелем, який виходить за межі панелей через зазор між ними. Прокладки між панелями мають Г-подібну форму і виконані із можливістю обмеження руху поворотних важелів. Передня панель містить прозору зону огляду у формі прямокутника зі сторонами, паралельними краям панелі, в межах якого переміщується вікнопаралелограм. Непрозора частина передньої панелі і рухомі пластини мають однакове забарвлення, яке відрізняється від кольору поверхні задньої панелі, що проглядається через вікно-паралелограм. Пропонована сукупність конструктивних елементів наочного посібника дозволяє підвищити дидактичний ефект, сприяє швидкому засвоєнню математичних понять. На фіг. 1 зображено загальний вигляд посібника. На фіг. 2, 3, 4 - його фронтальна проекція, без передньої панелі, із розміщенням вікна-паралелограма, що демонструє вихідний і два перетворені визначника. Тонкими лініями показані межі зони огляду і координатні осі, виконані на передній панелі. Наочний посібник містить передню панель 1 із прозорого матеріалу з нанесеною на її поверхні декартовою системою координат (фіг. 1) і паралельну їй задню панель кріплення 2. Між панелями 1 і 2 змонтовані пластини 3-6 (фіг. 2), виконані у формі півплощин, які утворюють своїми прямими ме жами вікно у вигляді паралелограма ОАВС, через яке проглядається поверхня панелі 2. Пластини 36 кріпляться шарнірно до панелі 2, відповідно: в точці 0 - пластини 3 і 5; в точці А – пластина 6; пластина 4 - в точці 7, яка є перетином прямої межі цієї пластини з віссю ординат. Пластини 3 і 4 стержнем 8 з’єднані між собою шарнірно в точках 9 і 10 так, що точки 0, 7, 9, 10 є вершинами шарнірного паралелограма. Аналогічно, пластини 5 і 6, розміщені поверх пластин 3 і 4, стержнем 11 з'єднані між собою шарнірно в точках 12 і 13. До пластин З і 5 жорстко прикріплені поворотні важелі 14 і 15, які виходять за межі панелей через зазори між ними. Відстань між панелями 1 і 2 визначається товщиною пластин 4 і 6 і регулюється Г-подібними прокладками 16, які служать одночасно обмежниками повороту важелів 14 і 15. Для підвищення дидактичного ефекту на панелі 1 прозорою є тільки зона огляду у вигляді прямокутника (фіг. 1), зі сторонами, паралельними краям панелі, в межах якого зміщується паралелограм ОАВС. Забарвлення пластин 3-6 і непрозорої частини панелі 1 однакове і відрізняється від кольору задньої панелі 2. Сторони ОА і ОС імітують радіус-вектори OA і OC , координати яких беремо в ролі першого і другого рядка визначника другого порядку. Наочний посібник використовують таким чином. Хай необхідно продемонструвати геометричний зміст визначника другого порядку. Рухом до упору важеля 14 вгору і важеля 15 вправо приводимо пристрій у вихідне положення (фіг. 2), демонструючи при цьому паралелограм ОАВС. Хай OA = {a1 , b1} і OC = {a 2 , b2 } . Тоді цим векторам (паралелограму ОАВС) відповідає визначник D= де: D a1 b1 a 2 b2 = a1b2 - a 2 b1 , - визначник другого порядку, верхній рядок якого є координати вектору OA , а нижній - координати вектору OC ; a1 , b1 - координати вектору OA у декартовій системі координат (ХОУ); a 2 , b2 - координати вектору OC у декартовій системі координат (ХОУ); D - позначка визначника другого порядку. Рухом важеля 15 вліво до упору (до суміщення сторони ОС з віссю ординат) перетворюємо вихідний паралелограм ОАВС в ОАВ1С1 (фіг. 3). Бачи мо, що вектор OA , тобто перший рядок визначника, і площа паралелограма залишились без змін. Із рівняння прямої СВ x - a 2 y - b2 = , a1 b1 ì ba ü виходить, що OC = í0, b2 - 1 2 ý . Отже, паралелоa1 þ î граму ОАВ1С1 відповідає визначник 2 37168 D1 = a1 b1 b a = a1b2 - a 2b1 , 0 b2 - 1 2 a1 де: D2 - визначник другого порядку, верхній рядок якого є координати вектору OA1 , а нижній - координати вектору OC1 ; А тому як де D1 - визначник другого порядку, верхній рядок a b S OA B C = OA 1 OC1 = a1 × b2 - 2 1 = a1b2 - a 2 b1 , 1 2 1 a1 якого є координати вектору OA , а нижній - координати вектору OC1 ; то маємо ba 0, b2 - 1 1 - координати вектору OC1 в декартовій a системі координат: Рухом важеля 14 вниз до упору (до суміщення сторони ОА з віссю абсцис) перетворюємо паралелограм ОАВ1С1 в ОА1В2С1 (фіг. 4). Бачимо, що отриманий прямокутник ОА1В2С1 рівновеликий ОАВ1С1, а відповідний йому визначник D = D1 = D 2 = SOA1B2 C1 = S OA1B1C1 = SOABC , де: SOA1B2C1 , SOA1B1C1 , SOABC - площа прямокутників OA1B2C1, OA1B1C1 та OABC, відповідно. Отже, визначник другого порядку чисельно дорівнює площі паралелограма, збудованого на векторах - рядках цього визначника. Аналогічний висновок отримаємо і відносно стовпців, якщо OA і OC1 розглядати як вектори - стовпці визначника. Таким чином, застосування наочного посібника дозволяє вдосконалити процес сприйняття математичних понять шляхом ілюстрації геометричного змісту визначника другого порядку за допомогою пропонованого наочного посібника. a1 0 a b = a1b2 - a 2b1 D2 = 0 b2 - 2 1 a1 Фіг. 1 3 37168 Фіг. 2 Фіг. 3 4 37168 Фіг. 4 __________________________________________________________ ДП "Український інститут промислової власності" (Укрпатент) Україна, 01133, Київ-133, бульв. Лесі Українки, 26 (044) 295-81-42, 295-61-97 __________________________________________________________ Підписано до друку ________ 2001 р. Формат 60х84 1/8. Обсяг ______ обл.-вид. арк. Тираж 50 прим. Зам._______ ____________________________________________________________ УкрІНТЕІ, 03680, Київ-39 МСП, вул. Горького, 180. (044) 268-25-22 ___________________________________________________________ 5