Пристрій для виявлення помилок у модулярній системі числення

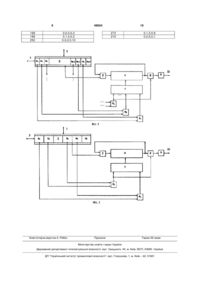
Пристрій для виявлення помилок у модулярній системі числення (МСЧ), що містить регістр числа у МСЧ, блок нулевізації (БН), перший блок констант нулевізації (БKH), блок аналізу значення лишка γn+1 на нуль (БА), першу групу елементів 3 49054 Найбільш близьким за технічною суттю до запропонованої корисною моделі є пристрій виявлення помилок у модулярній системі числення, що описано у літературі (Акушский И.Я., Юдицкий Д.И. Машинная арифметика в остаточних классах. М.: Сов. радио, 1968. с.349-353, рис.6.41). Пристрій містить регістр числа у МСЧ, блок нулевізації (БН), перший блок констант нулевізації (БKH), блок аналізу значення лишка n+1 на нуль (БА), першу групу елементів АБО, при цьому інформаційний вхід пристрою підключено до першого входу регістра, а керуючий вхід пристрою підключено до другого входу регістра, вихід якого та вихід БН через першу групу елементів АБО підключено до першого входу БН, а вихід БА є виходом пристрою. Найближчий аналог функціонує наступним чином. Перший етап. Вихідне перевіряємо число виду (a10 0 , a2 0 0 , ai 01,..., an 0 , an 1) заноA A ,..., ai ситься в регістр. Далі у БН послідовно приводиться до виду A(H)=(0, 0, ..., 0, 0, λn+1) за допомогою такої послідовності операцій віднімання, що не приведе до виходу числового значення числа А(0) за робочий діапазон [0,М). Ця операція в МСЧ називається нулевізацією, та складається в послідовному відніманні за однією основою цифр числа а1, а2, а3, ..., та аn з вихідного числа А(0) мінімальних чисел, так званих констант нулевізації (KН) виду 0 A (0, 0,..., 0, ai i i 1 1 1 i , ai i 1 ,..., an 1 i , an 4 KН(1)=(t1,1, t2,1, t3,1, ..., tn,1, tn+1,1), t1,1 (2) KH =(0, t2,2, t3,2, ..., tn,2, tn+1,2), t 2,2 1 m1 1 ; , 1 m2 , 1; (3) KH =(0, 0, t3,3, ..., tn,3, tn+1,3), t 3,3 1 m, 1 ; , KН(i)=(0, 0, ..., 0, ti,i, ti+1,i, ..., tn,i, tn+1,i), t i,i 1 mi 1 ; , KH(n)=(0, 0, ..., 0, tn,n, tn+1,n), t n,n 1 mn 1 . , Загальна кількість KH у БKH для даного пристрою дорівнює n. В цьому випадку число 0 0 0 A A 0 (a10 , a2 ,..., ai 0 , ai 01,..., an , an 1) (Н) довно приводиться до виду А , тобто A послі 0 0 0 (a10 , a2 ,..., ai 0 , ai 01,..., an , an 1) A0 A1 1 1 1 1 (0, a2 , a3 , ..., an , an 1) , A2 2 (0, 0, a3 , ..., an2 , an2 1) , 3 3 3 A 3 (0, 0, 0, a4 , ..., an , an 1) і так далі. Продовжуємо у БН віднімати n разів одержимо значення A n (H) n (0, 0, ..., 0, an 1) , або А =(0, 0, ..., an 0, n+1), де n+1= n 1 . Загальна схема віднімання А(і)=А(і-1)-KH(і) у БН пристрою представлена у наступному вигляді 1 1) KH (i) (0, 0, ..., 0, ai i 1 , t i 1,i , ..., t n,i , t n 1,i ) _______________________________________________________ Ai де [0, ..., 0, [ai i ai i 1 ai i 1 1 ai i (a i 1i1 tt ai i 1 ] modmi, [a i 1i1 ti i 1 1,i ] modmi 1, ..., [an 1 0. 1 1,i ) mod mi 1, Для даного пристрою (найближчого аналога) час нулевізації дорівнює значенню ТH1=2n , де: час віднімання з числа А(i-1) константи нулевізації KH(i); n - кількість інформаційних основ МСЧ. Другий етап. Після знаходження на першому етапі значення n+1, на другому етапі у схемі аналі an зу значення n+1= n 1 на нуль проводиться порівняння з нулем значення n+1. Якщо n+1=0 (число А знаходиться в діапазоні [0,М)), то робиться висновок, що число А не спотворено (правильне), тобто помилок нема. Якщо n+1≠0 (число А не знаходиться в діапазоні [0,М)), то число А спотворено (неправильне), тобто є помилка за однією з основ mi МСЧ. Загальний час Т1 виявлення помилок визначається як Т1=ТН1+ТП1, де ТП1 - час порівняння значення n+1 з нулем. В МСЧ час ТП1 порівняння виконується за один такт, тоді можна вважати, що Т1≈ТН1=2n (1). Недолік найближчого аналога - значний час Т1 визначення помилок. Це зумовлено значним часом ТН1 визначення числа n+1, тобто числа А(Н). tn 1,i modmn 1] , В основу запропонованої корисної моделі поставлено технічну задачу зменшення у часу Т виявлення помилок у МСЧ. Задача вирішується тим, що у пристрій для виявлення помилок у МСЧ, що містить регістр числа у МСЧ, блок нулевізації (БН), перший блок констант нулевізації (БKH), блок аналізу значення лишка n+1 на нуль (БА), першу групу елементів АБО, при цьому інформаційний вхід пристрою підключено до першого входу регістра, а керуючий вхід пристрою підключено до другого входу регістра, вихід якого та вихід БН через першу групу елементів АБО підключено до першого входу БН, а вихід БА є виходом пристрою, згідно корисної моделі, додатково введено (к-1)-н БKH, другу групу елементів АБО та групу елементів І, при цьому виходи розрядів регістру попарно а1, аn; а2, аn-1; а3, аn-2; і т.д. підключено до входів відповідних БKH, виходи яких через другу групу елементів АБО підключено до другого входу БН, вихід якого підключено до перших входів елементів І, до других входів яких підключено вихід к-го БKHк, а виходи елементів І групи підключено до входу БА. Введення вказаних ознак дозволяє суттєво зменшити час Т виявлення помилок у МСЧ. 5 49054 На Фіг.1 представлена блок-схема запропонованого пристрою. На Фіг.2 представлена блок-схема запропонованого пристрою для МСЧ з m1=3, m2=4, m3=5, m4=7, mn+1=m5=11. В таблиці 2 представлені константи нулевізації (БKH1). В таблиці 3 представлені константи нулевізації (БKH2). На Фіг.1 представлена блок-схема запропонованого пристрою, де: 1 - інформаційний вхід пристрою; 2 - регістр числа А=(а1, а2,...,аn+1); 3 - керуючий вхід пристрою; 4 - блок нулевізації; 5 - перша група елементів АБО; 61-6к(к=[n/2]) - група блоків констант нулевізації; 7 друга група елементів АБО; 8 - група елементів І; 9 - блок аналізу значення n+1 на нуль; 10 - вихід пристрою. На рисунку (Фіг.2) представлена блок-схема запропонованого пристрою для МСЧ з m1=3, m2=4, m3=5, m4=7, mn+1=m5=11. Інформаційний 1 вхід пристрою підключено до першого входу регістра 2, а керуючий 3 вхід підключено до другого входу регістра 2, вихід якого та вихід БН 4 через першу 5 групу елементів АБО підключено до першого входу БН 4. Виходи розрядів регістра 2 попарно аi(i-1), аn-і+1(i-1) (для i 1, n / 2 , для n парного), тобто, а1(0), аn(0); а2(1), аn-1(2); а3(2), аn(2) (n/2) , an/2+1(n)/2), або а1(0), аn(0); а2(1), аn-1(1); 2 ; ..., an/2 (2) (2) а3 , аn-2 ; ..., а(n+1)/2((n+1)/2-1) (для n непарного) підключено до пари входів відповідних БKH групи 616к, виходи яких через другу 7 групу елементів АБО підключено до другого входу БН 4, вихід якого підключено до перших входів елементів І групи 8, до других входів яких підключено вихід к-го БKH 6к. Виходи елементів І групи 8 підключено до входу БА 9, вихід якого є виходом пристрою. Даний пристрій відрізняється від найближчого аналога першим етапом його реалізації, тобто операцією визначення числа n+1. Сутність визначення значення n+1 у запропонованої корисної моделі полягає у тому, що процес нулевізації здійснюється паралельно за часом та одноразово за двома основами: аi(i-1), аn-і+1(i-1) МСЧ (для i 1, n / 2 , для n парного), тобто, а1(0), аn(0); а2(1), аn-1(2); а3(2), аn(2) (n/2) , an/2+1(n)/2), або а1(0), аn(0); а2(1), аn-1(1); 2 ; ..., an/2 а3(2), аn-2(2); ..., а(n+1)/2((n+1)/2-1) (для n непарного). В цьому випадку для даної корисної моделі KH мають наступний вигляд KН(1)=(t1,1, t2,1, t3,1, ..., tn,1, tn+1,1), t1,1 t n,1 t 2,2 0, mn 1 ; KH(2)=(0, t2,2, t3,2, ..., tn-1,2, 0, m1 1 ; 0, tn+1,2), 0,m 2 1; t n 1,2 0, mn 1 1 ; KH(n/2)=(0, 0, ...0, tn/2,n/2, tn/2+1,n/2, 0, ...0, tn+1,n+1), t n / 2,n / 2 0, mn / 2 ; t n / 2 1,n / 2 0, mn / 2 1 . Це для парного n=2k значення. Для непарного значення n=2k+1 маємо KH((n+1/2)=(0, 0, ..., 0, t(n+1)/2,(n+1)/2, 0, ... 0, tn+1,(n+1)/2), де t (n 1) / 2,(n 1) / 2 1 m(n 1) / 2 . Загальна , кількість KH для даного способу дорівнює n/2 для n парного, або (n+1)/2 - для непарного n. 6 У цьому разі вихідне число 0 0 0 A 0 (a10 , a2 ,..., ai 0 , ..., an , an 1) за к=[n/2] тактів послідовно перетворюється у число А(Н)=(0, 0, ..., 0, n+1) наступним чином A0 A A1 0 0 0 (a10 , a2 ,..., ai 0 , ai 01,..., an , an 1) , 1 1 1 1 (0, a2 , a3 ,..., ai1 , ai11,..., an 1, 0, an 1) , 2 1 1 A 2 (0, 0, a3 , a3 ,..., ai 2 , ai 21,..., an 2 , 0, 0, an2 1) , …. Для n парного маємо A n/ 2 1 (0, 0,..., 0, a(n/ /22 n (n/2) 1) , a(n/ /22 11), 0,..., 0, a(n /12 n n 1) ), (H) A =A =(0, 0, ..., 0, n+1). Для непарного n отримуємо 1) / 2 1) (0, 0, ..., 0, a((n 11)/ /22 (n ) ((n+1)/2) A ((n (H) 1) , 0, ..., a((n1 1) / 2 n 1) ), A =A =(0, 0, ..., 0, n+1). Очевидно, що час ТН2 нулевізації для найближчого аналога зменшується у два рази, тобто, ТН2=n , і час Т2 виявлення помилок відповідно дорівнює Т2≈ТH2=n (2). Пристрій для виявлення помилок у модулярній системі числення функціонує наступним чином (Фіг.1). На вхід 1 регістра 2 подається число 0 0 0 A A 0 (a10 , a2 ,..., ai 0 , ai 01,..., an , an 1) у МСЧ, і по сигналу шини 3 це значення через першу 5 групу елементів АБО поступає на перший вхід БН 4. Одноразово, по значенням а1(0), аn(0) у першому 61 БKH1 визначається перша KH виду KН(1)=(t1,1, t2,1, ..., tn,1, tn+1,1), t1,1 0, m1 1 ; t n,1 0, mn 1 . У БН 4 проводиться операція віднімання А(1)=А(0)-KH(1). Далі по сигналу шини 3 це значення А(1) через першу 5 групу елементів АБО поступає на перший вхід БН 4. Одноразово, по значенням а2(1), аn-1(1) у другому 62 БKH2 визначається друга KH виду KH(2)=(0, t2,2, t3,2, ..., tn-1,2, 0, tn+1,2), t 2,2 0,m2 1; t n 1,2 0, mn 1 1 . У БН 4 проводиться операція віднімання А(2)=А(1)-KH(2). Зрештою, по сигналу шини 3, значення A n / 2 1 (0, 0,..., 0, a(n/ /22 1), a(n/ /22 11), 0,..., 0, a(n /12 1) ) , n n n через першу 5 групу елементів АБО поступає на перший вхід БН 4. Одноразово, по значенням аn/2(n/2), аn/2+1(n)/2), у останньому 6к БKHк визначається KH виду KH(n/2)=(0, 0, ...0, tn/2,n/2, tn/2+1,n/2, 0, ...0, tn+1,n+1), t n / 2,n / 2 0, mn / 2 ; t n / 2 1,n / 2 0, mn / 2 1 . В цьому випадку з виходу значення А((n+1)/2)=А(Н)=(0, 0, ..., 0, n+1) поступає на перші входи елементів І групи 8, що відкриваються вихідним сигналом БKHк 6к. У схемі 9 аналізу значення n n 1 n+1= a на нуль проводиться порівняння з нулем значення n+1. Якщо n+1=0 (число А знаходиться в діапазоні [0,М)), то робиться висновок, що число А не спотворено (правильне), тобто помилок нема. Якщо n+1≠0 (число А не знаходиться в діапазоні [0,М)), то число А спотворено (неправильне), тобто є помилка за однією з основ mi МСЧ. На виході 10 7 49054 пристрою фіксується результат виявлення помилок. Наведемо приклади конкретної реалізації (Фіг.2) операції виявлення помилок у системі обробки цифрової інформації, що функціонує у МСЧ, що задана основами m1=3, m2=4, m3=5, m4=7, m5=11 (n=4). При цьому робочий діапазон дорів4 нює M mi 3 4 5 7 420 m, а повний діапа i 1 зон дорівнює М1=Мmn+1=420·11=4620 (табл.1). Приклад 1 Нехай треба виявити факт появи помилки для 8 A (2) (0, 0, 0, 0, 7) . Таким чином, А(2)=А(Н)=(0, 0, 0, 0, 7), тобто 5=7 ( 5≠0). Висновок: число А(0)=(1, 1, 0, 1, 4) має помилку за однією з основ mi ( i 1,4 ) МСЧ. Перевірка: число А(0) в ПЗЧ дорівнює значенню А(0)=3865>420 (табл.1). Таким чином, запропонована корисна модель дозволяє незалежно від довжини 1-байтового машинного слова (тобто від кількості n основ МСЧ) у два рази, в порівнянні з прототипом, зменшити час виявлення помилок у МСЧ. Таблиця 1 0 0 0 0 числа A A 0 (a10 , a2 , a3 , a 4 , a5 ) (1 0, 0,1 4) , , у МСЧ (табл.1). Для цього у першому БKH1 61 [0,Мi), i 0,10 0÷419 420÷839 840÷1259 1260÷1679 1680÷2099 2100÷2519 2520÷2939 2940÷3359 3360÷3779 3780÷4199 4200÷4619 0 (табл.2) за цифрами a10 1 та a 4 1 вибираємо (1) константу нулевізації у вигляді KH =(t1,1, t2,1, t3,1, t4,1, t5,1), де повинно бути t1,1=a1=1 та t4,1=а4=1. В цьому випадку з БKH1 вибираємо KH(1)=(1, 1, 1, 1, 1) (табл.2). Далі у БН 4 проводимо операцію А(1)=А(0)-KH(1), тобто _А(0)=(1, 0, 0, 1, 4) KH(1)=(1, 1, 1, 1, 1) A (1) (0, 3, 4, 0, 3) , та паралельно у часі для числа А(1)=(0, 3, 4, 0, 3) з БKH2 62 (табл.3) вибираємо KH(1)=(0, t2,2, t3,2, 0, 1 t5,2) для якої потрібно щоб було a2 t 2,2 0 2 4 6 8 10 1 3 5 7 9 3 та Таблиця 2 (2) 1 a3 t 3,2 4 . В цьому випадку KH визначиться (2) як KH =(0, 2, 3, 0, 4). Далі БН 4 визначає різницю А(2)=А(1)-KH(2), тобто _А(1)=(0, 2, 3, 0, 4) KH(2)=(0, 2, 3, 0, 4) A (2) (0, 0, 0, 0, 0) . Число А(2), через відкриті вихідним сигналом БKH2 62 елементи І групи 8, поступає на вхід БА 9. Таким чином, одержано нулевізоване число виду А(2)=А(Н)=(0, 0, ..., 0, ..., 0, n+1)=(0, 0, 0, 0, 5), де (0) 5=0. Висновок: число А =(1, 0, 0, 1, 4) не має помилок. Перевірка: число А(0) в позиційній системі числення дорівнює А(0)=400, тобто знаходиться в межах робочого числового [0,419] інтервалу (табл.1). Приклад 2 Нехай треба виявити факт появи помилки для 0 0 0 0 числа A A 0 (a10 , a2 , a3 , a4 , a5 ) (1 1 0,1 4) . ,, , В цьому випадку в регістр 2 поступає це число, a BKH1 61 (табл.2) визначає KH(1)=(1, 1, 1, 1, 1). Далі БН 4 визначає А(1)=А(0)-KH(1), тобто _А(0)=(1, 1, 0, 1, 4) KH(1)=(1, 1, 1, 1, 1) A (1) (0, 0, 4, 0, 3) . Для отриманого числа А(1) з блоку констант (2) нулевізації 62 (табл. 3) вибираємо KH =(0, 0, 4, 0, 1 1 7), де a2 t 2,2 0 та a3 (2) (1) (2) чає А =А -KH _А(1)=(0, 0, 4, 0, 3) KH(2)=(0, 0, 4, 0, 7) n+1= 5 t 3,2 4 , а БН 4 визна ПСС 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 m1=3, m4=7 1,1,1,1,1 2,2,2,2,2 0,3,3,3,3 1,0,4,4,4 2,1,0,5,5 0,2,1,6,6 1,3,2,0,7 2,0,3,1,8 0,1,4,2,9 1,2,0,3,10 2,3,1,4,0 0,0,2,5,1 1,1,3,6,0 2,2,4,0,3 0,3,0,1,4 1,0,1,2,5 2,1,2,3,6 0,2,3,4,7 1,3,4,5,8 2,0,0,6,9 Таблиця 3 ПСС 21 84 105 42 63 126 147 m2=4, m3=5 0,1,1,0,10 0,0,4,0,7 0,1,0,0,6 0,2,2,0,9 0,3,3,0,8 0,2,1,0,5 0,3,2,0,4 9 168 189 252 49054 0,0,3,0,3 0,1,4,0,2 0,0,2,0,10 Комп’ютерна верстка А. Рябко 10 273 210 Підписне 0,1,3,0,9 0,2,0,0,1 Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601