Пристрій для рішення оптимальних задач

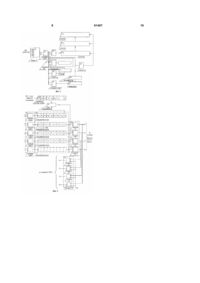
Пристрій для рішення оптимальних задач, що містить n груп із m блоків задання показників, n груп із елементів АБО, n суматорів та n блоків вибору мінімального коду, матрицю ідентифікації із mхn елементів, кожна і-та група з яких містить 2 81407 1 3 81407 опубл.15.09.1993, Бюл.. №30 - С.37], який містить в собі групу із m блоків задання показників ідентифікації об'єкту (процесу), групу із n суматорів (n - кількість типів ідентифікуємих об'єктів (процесів)), блоку вибору мінімального коду, генератора одиночних імпульсів, елемент затримки, група із m елементів затримки, групу із n елементів "АБО", групу із m´n елементів ідентифікації, кожен з яких містить регістр та блок розрахунку . Пристрій виконує рішення задачі оптимізації згідно заданим критеріям, вибираючи із n типів об'єктів ідентифікації за мінімальними показниками. Недоліком відомого пристрою є те, що він не виконує ітераційних процесів оптимізації, шляхом поступового наближення до мінімального значення показників за декілька циклів (ітерацій). За перший цикл знаходиться оптимальний об'єкт за показниками ідентифікації. Опис цього об'єкту з виходу пристрою надходить на його вхід для проходження другого циклу оптимізації. Процес повторюється, якщо показники останнього циклу кращі (або відрізняються) від попереднього. Якщо показники не відрізняються, процес оптимізації зупиняється. Прикладом такої послідовної оптимізації є мінімізація кількості станів автоматів Мілі за алгоритмом, запропонованим Ауфенкампом та Хоном. Із теорії автоматів відомо, що абстрактний автомат - це дискретний пристрій, який визначається множиною вхідних сигналів Z={z1,z2,...,zn}, множиною вихідних сигналів W={w1,w2,...,wm } і множиною внутрішніх станів А={а1,а2,...,аk}, функцією переходів d та функцією виходів l. Існує декілька засобів завдання (опису) роботи автомата, із яких частіше використовують таблиці переходів а=d(a, z) та виходів w=l(a, z). Наведемо приклад задання автомату А табличним засобом. У таблиці 1.1 і таблиці 1.2 наведені таблиці переходів і виходів відповідно. У таблицях можуть бути однакові стани, які називають еквівалентними. Таблиця 1.1 4 сигнали при будь-яких вхідних. При мінімізації станів автомата за таблицею 1.2 (таблицею виходів), знаходять p1-розбиття на 1-класи еквівалентності, об'єднуючи в еквівалентні класи однакові стовпці: p1={В1В2,}, де В1={а1,а2,а5,а6}, В2={а3,а4} Побудуємо таблицю p1-розбиття, замінюючи у таблиці 1.1 стани відповідними класами еквівалентності. Таблиця 1.3 Таблиця p1–розбиття B1 a1 B2 B1 z1 z2 a2 B2 B1 B2 a5 B1 B1 a6 B1 B1 z1 z2 a2 a4 a6 a3 a3 a5 a4 a4 a6 Таблиця 1.4 Таблиця p2 – розбиття C1=D1 a1 a2 C3 C3 C2 C2 z1 z2 C2=D2 a5 a6 C2 C2 C1 C1 Результат другої ітерації порівнюємо з першим розбиттям. Вони різні. Треба продовжувати оптимізацію. Аналогічно знаходимо p3- розбиття за таблицею 1.4, яке збігається з p2 - розбиттям, D1,=C1, D2=С2, D3=C3. На цьому ітерації закінчуються. Тепер довільно із кожного класу С1, С2, С3 вибираємо по одному стану і одержуємо еквівалентний мінімізований автомат А'={а1,а4,а5}, а стани а2,а3,а6 виключаємо. Тоді таблиця переходів та виходів мінімального автомату матиме вигляд, показаний у таблицях 1.5 та 1.6 відповідно. a5 a5 a1 a6 a6 a2 Таблиця переходів мінімального автомату z1 z2 a1 a4 a5 a4 a4 a5 z1 z2 a3 w1 w1 a4 w1 w1 a5 a5 a1 Таблиця 1.6 Таблиця переходів a2 w1 w1 C3=D3 a3 a4 C3 C3 C2 C2 Таблиця 1.5 Таблиця 1.1 a1 w1 w1 a4 B2 B1 На цьому перша ітерація закінчилась. Аналогічно, за таблицею 1.3 отримуємо p2 розбиття на 2-класи еквівалентності: p2={С1,С2,С3}, де С1={а1,а2}, С2={а5,а6}, С3={а3,а4} Таблиця переходів a1 a3 a5 a3 B2 B1 a5 w1 w1 a6 w1 w1 Два стани автомата аi, аj називають 1еквівалентними, якщо вони мають однакові вихідні Таблиця виходів мінімального автомату z1 z2 a1 w1 w1 a4 w1 w2 a5 w1 w1 5 В основу запропонованого винаходу поставлено завдання розробити пристрій для рішення оптимальних задач синтезу об'єктів (процесу) з розширенням класу апаратної реалізації за рахунок задач мінімізації кількості внутрішніх станів цифрового автомату. Це дає змогу зменшити витрати при побудові цифрових автоматів за рахунок виключення "лишку" елементів пам'яті (тригерних схем) та логічних елементів керування ними. Вирішення завдання досягається тим, що до пристрою для рішення оптимальних задач, що містить n груп із m блоків задання показників, n груп із елементів АБО, n суматорів та n блоків вибору мінімального коду, матрицю ідентифікації із m´n елементів, кожна і-та група з яких містить регістр та блок розрахунку, причому і=1,n, генератор одиночних імпульсів, k елементів затримки, причому перші входи регістрів матриці ідентифікації та входи регістрів задання показників з'єднані з інформаційними входами пристрою, виходи регістрів задання показників та матриці ідентифікації з'єднані відповідно з першими та другими входами блоків розрахунку, а перші виходи блоків розрахунку кожної із n груп матриці ідентифікації підключені через елемент АБО на перший вхід суматора, перший вихід якого з'єднаний із першим входом блока вибору мінімального коду, вхід генератора одиночних імпульсів з'єднаний із входом пуску пристрою додатково введені n блоків зупинення оптимізації, генератор тактових імпульсів, при цьому перші виходи блоків вибору мінімального коду підключені до входів блоків зупинення оптимізації, другі виходи блоків вибору мінімального коду підключені до третіх входів блоків розрахунку, треті виходи блоків вибору мінімального коду підключені до других входів суматорів групи, другі виходи з суматорів підключені до других входів блоку зупинення оптимізації, перші виходи блоків зупинення оптимізації з'єднані з другими входами блоків вибору мінімального коду, другі виходи блоків зупинення оптимізації з'єднані із четвертими входами блоків розрахунку та другими входами регістрів задання показників, треті виходи з блоку зупинення оптимізації з'єднані з входами суматорів, вхід генератора тактових імпульсів підключений до виходу генератора одиночних імпульсів, вихід генератора тактових імпульсів підключений до входу першого елементу затримки, виходи кожного елементу затримки підключаються до відповідних тактових входів блоків пристрою, які сумісно дозволяють виконання задач оптимізації, зокрема мінімізацію станів цифрових автоматів за алгоритмом Ауфенкампа - Хона і саме цим забезпечують розширення класу рішення оптимальних задач за рахунок включення до них ітераційних процесів пошуку еквівалентних об'єктів (процесів) ідентифікації, що дозволяє використовувати сучасні інформаційні та нейрокомп'ютерні мережі для розв'язування задач ефективного синтезу структурованих систем із прогнозованою направленою поведінкою. 81407 6 Запропонований пристрій дозволяє виконувати одночасно оптимізацію n об'єктів по m показниках (станах), число яких може обмежуватися тільки кількістю та розрядністю регістрів блоку показників (таблиця переходів) та регістрів ідентифікаційної матриці (таблиця виходів). Але при сучасній базі логічних елементів, як замовлених так і стандартних програмованих логічних інтегральних схем (ПЛІС, PLD Programmable Logic Devices), число елементів у кожному за прогнозом досягне 2000000 у 2005 році, що знімає це обмеження. Кількість ітерацій, як правило, не досягає десятків, а швидкодія PLD (за тим же прогнозом) - 0,75 не знімає і це обмеження. Це забезпечує усій заявленій сукупності ознак відповідність критерію "новизна" та приводить до нових технічних результатів. Аналоги, які містять ознаки, що відрізняються від прототипу, не знайдені, рішення явним чином не випливає з рівня техніки. На підставі цього можна зробити висновок: пропоноване технічне рішення задовольняє критерію "винахідницький рівень". Ідея винаходу пояснюється на кресленні 1, де показана структурна схема пристрою для рішення оптимальних задач. Пристрій містить n груп блоків із m регістрів задання показників 11-1n, матрицю ідентифікації з n груп 21-2n, в яку входять m регістрів (стовпців таблиці виходу автомату) 31-3m, та m блоків розрахунку 41–4m, n груп із елементів АБО 51-5n, n суматорів 61-6n, n блоків вибору мінімального коду 71-7n, n блоків зупину оптимізації 81-8n, генератору одиночних імпульсів 9, генератор тактових імпульсів 10, блок із k елементів затримки 11. Робота запропонованого пристрою здійснюється наступним чином. Для спрощення викладу будемо пояснювати роботу запропонованого пристрою для першої групи із n груп. З інформаційних входів на пристрій надходить інформація показників переходів автомату із станів аi, де і=1,2,...,m до станів аj де i=1,2,...,m (таблиця 1.1), та інформація виходів (таблиця 1.2) до регістрів матриці ідентифікації. За командою "Пуск" генератор одиночних імпульсів 9 включає генераторів тактових імпульсів 10 і першим TI0 ця інформація записується до регістрів блоку 11 та 31-3m. За тактовим імпульсом ТІ1 дані а1 стовпця виходів з регістру 31 через блок розрахунку 41 елемент АБО 51 надходить до суматора 61. За тактовим імпульсом ТІ2 дані а2 стовпця виходів з регістру 32 аналогічним шляхом надходять до суматора 61 у додатковому коді та додаються (тобто віднімаються). Якщо стовпці мають однакові коди, то на виході суматора 61 по всім розрядам буде машинний нуль, який фіксується блоком вибору мінімального коду 71 записом на місці стовпців a1 та а2 коду B1. За таким алгоритмом проходить зрівнювання всіх стовпців виходів по схемі а1, із а2, а3,...,аm . Усі пари стовпців із однаковими кодами фіксуються блоком вибору мінімального коду 71 записом до розряду регістру а1 одиниці, а в інших 7 розрядах, де коди стовпців різні, записуються нулі. Це добре пояснюється на фігурі 2, на якій приведена структурна схема блоку вибору мінімального коду 71. Нулі від суматору 61 подаються на логічну схему "І" 12 через інверсні входи. При збіжності нулів до розряду регістру 151 за тактовим імпульсом ТІ, що приходить на вхід елементу "АБО" 13, вихід якого з'єднаний із входом елементу "І" 14, одиниця, при розбіжності нуль, після запису регістр 31 зсувається на один розряд праворуч. Крім запису до регістру 151, ця інформація про збіги (та розбіжності) записується до лічильника 16 та лічильника 21. Лічильник 16 являє собою лічильник, з'єднаний із елементом "І", на вхід якого (елемента "І") надходить інформація із виходу елемента "АБО" 13 та виходу тригера 17. Лічильник 16 при першій же розбіжності зупиняє рахування за сигналом тригера 17, до входу якого підключений інвертор 18, і на виході лічильника 16 сформується код номера розряду а1, до якого записано перший нуль. Лічильник 21, інформація до якого надходить через елемент "АБО" 19 із одним інверсним входом, з виходу елементу "АБО" 13, рахує розряди регістру 151. Якщо при зсуві праворуч інформація дійде до крайнього розряду, спрацює дешифратор 20. Його сигнал закриє вхід регістра 151, через елемент "І" 14, та перепише через інвертор 11 код регістру 151, до регістру 152, код регістра 152 до регістру 153, тощо. Таким чином, одержуємо у регістрі 15, код першого p1,- розбиття В1-еквівалентності. Ті розряди, де є одиниця відображають а1, які відносяться до B1 - еквівалентності. Пошук В2 - еквівалентність починається із зрівнювання стовпців із а1, код якого записаний у лічильнику 16. Інші еквівалентності В3,В4,...,Вf формуються аналогічно першому, в результаті яких формується у регістрах 151,152,...,15l інформація p1, - розбиття. Перейдемо до структурної схеми пристрою для рішення оптимальних задач. Блоки розрахунку 41–4m , на які подається інформація p1- розбиття із блоку вибору мінімального коду 7l, та інформація з блоку задання показників l1, формують дані типу таблиці 1.3 та записують її послідовним кодом до регістрів 31,32...,3m. Роботу блоку розрахунку 4, можна пояснити за допомогою структурної схеми, представленої фігурою 3. Інформація p1 - розбиття із блоку вибору мінімального коду 71 подається на перші входи елементів "АБО" блоку 25 та послідовно із прив'язкою до станів а1,а2,...,аr записуються до кільцевих регістрів блоку 26. Після запису інформації від блоку задання показників l1, робиться зрівнювання розряду а1 кільцевих регістрів блоку 26 з усіма станами кільцевого регістру станів 23. На тих станах, де їх коди зрівнюються, виробляється сигнал запису відповідного розряду а1 кожного з кільцевих регістрів блоку 26 через схеми "І" блоку 27 до регістру 31 матриці ідентифікації 21, формуючи цим опис p1-розбиття (таблиця 1.3). Коли кільцевий регістр станів 23 зробить один цикл повного зсуву, робиться зсув на один розряд 81407 8 кільцевих регістрів блоку 26. Після цього цикл зсуву кільцевого регістру станів 23 повторюється. За таким алгоритмом зрівнюються всі стани від а1 до аr. По других входах елементів "АБО" блоку 25 подається інформація мінімального коду станів із блоку зупинення оптимізації 81. Блок зупину оптимізації 81 зберігає у своїх регістрах попередню інформацію p1-розбиття на класи еквівалентності і зрівнює її із інформацією, яка надходить від суматора 61 та від блоку вибору мінімального коду 71. До суматора 61 дані надходять із виходу блоку вибору мінімального коду 71 . Якщо зрівнювані значення дорівнюють один одному, то формується сигнал зупинення оптимізації. У кожному розбитті перетворюються у нулі всі еквівалентні стани, крім одного, які і записуються до регістрів блоку задання показників 11 та регістрів 31, 32,...3m матриці ідентифікації 21 як оптимальні (таблиця 1.5). Виходячи з вищевикладеного, можна зробити висновок, що пропоноване технічне вирішення задовольняє вимогам критерію "Промислова застосовність". 9 81407 10