Рекурентний спосіб оптимального керування комплексуванням вимірників при нерівно точних вимірах фізичних величин
Номер патенту: 45289
Опубліковано: 10.11.2009
Автори: Нікулін В'ячеслав Ігорович, Конахович Георгій Филимонович, Ігнатов Володимир Олексійович, Кудренко Станіслава Олексіївна
Формула / Реферат
Рекурентний спосіб оптимального керування комплексуванням вимірників при нерівно точних вимірах фізичних величин, у якому для вимірювання значення фізичної величини послідовно, такт за тактом, застосовують m≥2 вимірювальних систем з різними погрішностями вимірювань, результати вимірювань запам'ятовують і по них за допомогою формул непрямих вимірювань обчислюють істинне значення фізичної величини, який відрізняється тим, що оптимальну оцінку Xopt(k) результату вимірювань на k-ому такті розраховують за рекурентною формулою непрямих вимірювань:
![]()
![]()
де ![]() ,
, ![]() - відповідно, оптимальні результати вимірювань на
- відповідно, оптимальні результати вимірювань на ![]() -му та
-му та ![]() -му тактах,
-му тактах,
![]() - оптимальний ваговий коефіцієнт вимірювань на
- оптимальний ваговий коефіцієнт вимірювань на ![]() -му такті,
-му такті,
![]() ,
,![]() - відповідно, дисперсії вимірювань на
- відповідно, дисперсії вимірювань на ![]() -му та
-му та ![]() -му тактах,
-му тактах,
![]() - результат вимірювань на
- результат вимірювань на ![]() -му такті,
-му такті,
m - загальне число тактів вимірювань,
як суму оптимального результату Хорt(k-1) вимірювань на попередньому, (k-1)-ому такті, і різниці ![]() між результатом вимірювання Yk на поточному, k-ому такті, і оптимальним результатом Xopt(k-1), помноженої на оптимальний ваговий коефіцієнт k-ого такту
між результатом вимірювання Yk на поточному, k-ому такті, і оптимальним результатом Xopt(k-1), помноженої на оптимальний ваговий коефіцієнт k-ого такту
![]() ,
, ![]()
який вибирають оптимально по критерію мінімуму дисперсії Xopt(k) шляхом розв'язання системи з двох рівнянь оптимізації значень вагових коефіцієнтів при Xopt(k-1) та Yk з урахуванням необхідної умови незміщеності оптимальної оцінки Xopt(k), на k-ому такті розраховують мінімальне значення дисперсії Dmin(k) оптимальної комплексної оцінки Xopt(k) за рекурентною формулою непрямих вимірювань:
Dmin(k)=gopt(k)Dk ,
де Dmin(k) - мінімальне значення дисперсії на k-ому такті,
Dk - дисперсія Yk,
середнє квадратичне значення оптимальної комплексної оцінки Xopt(k),
![]() ,
,
мінімальне значення коефіцієнта варіації оптимальної комплексної оцінки Xopt(k),
![]() ,
,
різницю, що характеризує зменшення коефіцієнта варіації в k-ому і (k-1 )-ому тактах,
![]() ,
,
відносне значення зменшення коефіцієнта варіації в k-ому і (k-1)-ому тактах
![]() ,
,
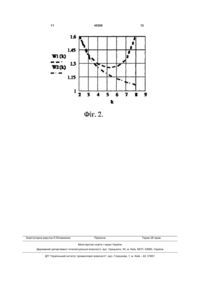
індексний показник W1 порівняльної ефективності оптимального рекурентного способу оцінювання відносно вимірювань способом розрахунку середньоарифметичного значення:
![]() ,
,
де D0(m) є дисперсія середньоарифметичного значення, при розрахунку якого всі вагові коефіцієнти тактів вибирають однаковими і рівними 1/m:
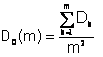 ,
,
індексний показник W2 порівняльної ефективності оптимального рекурентного способу оцінювання відносно паралельного гетерогенного оптимального способу вимірювань отримують за формулою непрямих вимірювань:
![]() ,
,
де D2(m) є дисперсія паралельного оптимального гетерогенного способу з m вимірювань:
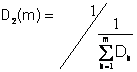 .
.
Текст
Рекурентний спосіб оптимального керування комплексуванням вимірників при нерівно точних вимірах фізичних величин, у якому для вимірювання значення фізичної величини послідовно, такт за тактом, застосовують m≥2 вимірювальних систем з різними погрішностями вимірювань, результати вимірювань запам'ятовують і по них за допомогою формул непрямих вимірювань обчислюють істинне значення фізичної величини, який відрізняється тим, що оптимальну оцінку Xopt(k) результату вимірювань на k-ому такті розраховують за рекурентною формулою непрямих вимірювань: 3 45289 4 індексний показник W2 порівняльної ефективності оптимального рекурентного способу оцінювання відносно паралельного гетерогенного оптимального способу вимірювань отримують за формулою непрямих вимірювань: D2 (m) W2 (m) = , Dmin (m) де D2(m) є дисперсія паралельного оптимального гетерогенного способу з m вимірювань: . 1 Корисна модель відноситься до вимірювальної техніки і стосується непрямих вимірювань фізичних величин, в тому числі і радіотехнічними системами, для загального випадку вимірювань місцезнаходження, напрямів, відстаней, рівнів, азимутів у навігації, коли з метою підвищення точності та вірогідності для вимірювання одного і того ж значення фізичної величини використовують декілька вимірювальних систем, що мають різні погрішності вимірювань. Відомим є спосіб нерівно точних вимірів [1], у якому використовують нормальну міру h точності системи з m нерівно точних вимірів не вказує, як необхідно вибирати вагові коефіцієнти. Ці два способи розглядають як аналоги пропонованого способу. Прототипом корисної моделі служить спосіб виміру фізичних величин за авторським посвідченням СРСР №1824589 [3]. Він полягає в тому, що в першому такті вимірюють фізичну величину X1 посилену (ослаблену) у К1 раз, у другому такті вимірюють фізичну величину Х2 посилену (ослаблену) у К2 разів, у третьому такті вимірюють фізичну величину Х3 посилену (ослаблену) у (K1+К2) разів, у четвертому такті вимірюють фізичну величину Х4 і обчислюють істинне значення фізичної величини по формулі непрямих вимірів X0=K1Y1+K2Y2 +(K1+ K2) Y3 + Y4 де Y1, ... Y4 - результати вимірів у першомучетвертому тактах, відповідно. В основу корисної моделі поставлено задачу оптимального визначення за критерієм мінімуму дисперсії погрішності результату вимірювань Xopt(k) на k-му такті за рекурентною формулою (5) непрямих вимірювань 2 h= m ∑ gi( X0 − Xi )2 κ =1 (1) m −1 де h – нормальна міра точності системи, gi - ваговий коефіцієнт і-го вимірювання, Х0 - оцінка значення параметру, що вимірюється, Хi - і-те значення результату вимірюваная. Коефіцієнт gi знаходять з умови h2 (2) gi = i , i=1, m, h2 де міра точності і-го вимірювання hi = 1 (3) 2D[Xi ] a D[Xi ] - дисперсія і-го вимірювання. Оцінку Х0 отримують по формулі непрямих вимірів m ∑ giopt Yi X0 = κ =1 (4) m ∑ giopt κ =1 Недоліком способу є неможливість вибору hі коли самі gі невідомі. Відомий також спосіб непрямих вимірювань фізичної величини шляхом послідовної тактової обробки результатів нерівно точних вимірів [2]. Цей спосіб не вимагає запам'ятовування всієї сукупності Y1, Ym, значень, що вимірюються, спрощує процедуру обробки і дозволяє обробити результати нерівно точних вимірювань у реальному масштабі часу. Але як і перший спосіб, цей спосіб D2 (m) = 1 m ∑ Dk k =1 X opt (k) = X opt (k - 1) + + k=2, m gk -1D k -1 X opt (k − 1) − Yk , gk -1D k -1 + D k [ ] (5) де Xopt(k-1), Xopt(k) – відповідно, оптимальні результати вимірювань на (k-1)-му та k-му тактах, gopt(k-1) – оптимальний ваговий коефіцієнт вимірювань на (k-1)-му такті, Dk-1, Dk – відповідно, дисперсії вимірювань на (k-1)-му та k-му тактах, Yk - результат вимірювань на k-му такті, m – загальне число тактів вимірювань, шляхом розв'язання на k-му такті системи з двох рівнянь оптимізації значень вагових коефіцієнтів при Хорt(k-1) і Yk з урахуванням умови несміщеності оптимальної оцінки Xopt(k). Максимальна точність результату непрямих вимірювань значення фізичної величини досягається тим, що в способі виміру фізичних величин за А.С. СРСР №1824589 [3] використовують по тактову (ітераційну) оптимальну процедуру оцінювання результату вимірювання фізичної величини X різними m вимірниками, для чого такт за тактом роблять m вимірювань Y1, Ym, в яких i-те вимірювання має значення (6) Yі= kіХ+ξi, і=1, m, 5 де kі є коефіцієнт передачі і-го перетворювача значення Х в Yi при вимірюванні, ξi є випадкова погрішність і-го вимірника, відносно якої припускається, що вона має гаусовський розподіл з математичним очікуванням і дисперсією (7) (7) М[ξi]=0, D[ξi]=Di, на k-ому такті оптимальну оцінку результату вимірювань отримують як суму оптимального результату Xopt(k-1) на (k-1)-ому такті і різниці Xopt(k-1)-Yk, між Xopt(k-1), і результатом вимірювання Yk на k-ому такті, помноженої на оптимальний ваговий коефіцієнт k-ого кроку (8) g(k - 1)D(k -1) gopt (k) = (8) g(k − 1) Dk -1 + Dk для чого значення Xopt(k-1), gopt(k), Yk для подальшої обробки запам'ятовують, ітераційну процедуру починають з другого такту (з другої ітерації), після отримання перших двох вимірювань, в цій ітерації задають gopt(1)=D2/(D1+D2), Xopt(1)=Y1 D[Xopt(1)] = D1 (9) за допомогою формули (10) непрямих вимірювань за апріорно відомої дисперсії Dk погрішності k-го вимірника на k-ому такті розраховують мінімальне значення дисперсії Dmin (k) оптимальної комплексної оцінки Xopt(k), Dmin(k) = gopt (k) Dk, (10) середнє квадратичне значення (11) оптимальної оцінки Xopt(k), σmin (k) = Dmin (k) (11) мінімальне значення коефіцієнта варіації (12) оптимальної комплексної оцінки Xopt(k), σ (k ) , Vmin (k ) = min (12) Xopt (k) різницю (13), що характеризує зменшення коефіцієнта варіації в k-ій і (k-1)-ій ітераціях ∆Vmin (k, k − 1) = Vmin (k ) − Vmin (k − 1) , (13) відносне значення зменшення коефіцієнта варіації в k-ій і (k-1)-ій ітераціях V (k ) − Vmin (k − 1) δmin (k, k − 1) = min . (14) Vmin (k ) Таким чином, на k-ій ітерації в чарунках памяті накопичують результати виконання попередньої і поточної ітерацій Xopt(k-1), Xopt(k), gopt(k-1), gopt (k), Dk-1, Dk, Vmin(k-1), Vmin(k), δmin(k-1), δmin(k), Yk, що дозволяє адаптивне управління процедурою вимірювань і припинення вимірювань тоді, коли відносна погрішність вимірювання (12) стає меншою заданої. На Фіг. 1 показана узагальнена структурна схема способу. Спосіб реалізується наступним чином. Цикл вимірювань починається з того, що з об'єкту вимірювання ОВ (блок 1) за сигналами управління СУ блока 2 управління та синхронізації БУС з бази даних БД 3 на блок 4 рекурентної обробки БРО результатів прямих вимірювань подаються сигнали Dk, k=1, m, що відображають апріорні значення дисперсій погрішностей вимірників на k-ій ітерації, а також сигнал X, який відображає вимірювану фізичну величину. БРО за командою БУС виконує операції за формулами непрямих обчислень (5)-(14), що в даному випадку відігра 45289 6 ють роль операторних рівнянь роботи певних функціональних пристроїв оптимального вимірювача. Після закінчення обчислень БРО за останньою командою БУС подає результати обчислень у вигляді сигналів Xopt(k-1), Xopt(k), gopt(k-1), gopt(k), Dmin(k-1), Dmin(k), σmin(k-1), σmin(k), Vmin(k-1), Vmin(k), δmin(k-1), δmin(k) на блок 5 відображення результатів вимірювань БВР у даному циклі. БВР відображає результати вимірювань. Якщо обчислення виконують у цифровій формі, у структуру оптимального обчислювача включають аналогове - цифрові та цифро - аналогові перетворювачі вхідних та вихідних сигналів. Як випливає з принципу роботи структурної схеми способу, в способі вхідні сигнали X та Dk згідно операторних рівнянь (5)-(14) перетворююсь у вихідні сигнали Xopt(k-1), Xopt(k), gopt(k-1), gopt(k), Dk-1, Dk Vmin(k-1), Vmin(k), δmin(k-1), δmin(k), Yk. Основна формула (5) непрямих вимірювань має рекурентний характер, тому цей спосіб названий рекурентним гетерогенним способом оптимального управління комплексуванням вимірювань m нерівно точних вимірювальних систем. Приклад 1. В цьому прикладі розглянуто результати експерименту, що був проведений методом статистичного імітаційного моделювання рекурентного способу. Експеримент виконувався при дотриманні наступних умов і припущень: 1. В ролі еталону було обрано детермінований параметр X=1. 2. Оптимальне управління комплексуванням виконувалося для m=8 нерівно точних вимірювальних систем в комплексі, що мав характеристичне число m0=9. 3. Дисперсії погрішностей вимірювальних систем були апроксимовані арифметичною убутною прогресію Dk=D1-(k-1)d, k=1, m, (15) що еквівалентно ранжируванню систем за порядком зменшення значень дисперсій погрішностей. 4. Обрано 20 % середню квадратичну погрішність для найбільш неточної системи, що досить повно відповідає реальному стану речей, тому D1 = 0.04. 5. Показник d прогресії (15) обрано так, щоб охопити ряд з 9 систем різного класу точності, в тому числі і еталонну систему, тому d=0.005, і у числовому вигляді Dk = 0.04- (k-1) 0.005 d, k =1, m, (16) 6. Для моделювання вимірювань прийнято припущення про однородність вимірювальних перетворювачів, тобто що усі kі=1, і=1, m. (17) 7. Результати вимірювань моделюються реалізаціями випадкових величин за допомогою функції (18) системи MathCAD (18) Yk = rnorm{N, M[X], σk}, k=1, m, де число реалізацій вибрано N=1, математичне очікування M[X]=X=1, середня квадратична погрішність σk = Dk 7 45289 8. Для моделювання роботи структурної схеми способу була розроблена програма РГС – m/m0. Вона дозволяє використовувати різні набори вхідних даних експериментів і виконувати статистичні експерименти при різних обсягах вибірок N і числі систем m
ДивитисяДодаткова інформація
Назва патенту англійськоюRecurrent method for optimal control of complexation of measuring devices at varying-accuracy measurements of physical values
Автори англійськоюIhnatov Volodymyr Oleksiiovych, Konakhovych Heorhii Filimonovych, Kudrenko Stanislava Oleksiivna, Nikulin Viacheslav Igorovych
Назва патенту російськоюРекуррентный способ оптимального управления комплексированием измерителей при неравноточных измерениях физических величин
Автори російськоюИгнатов Владимир Алексеевич, Конахович Георгий Филимонович, Кудренко Станислава Алексеевна, Никулин Вячеслав Игоревич
МПК / Мітки
МПК: G01C 3/00
Мітки: комплексуванням, нерівної, рекурентний, точних, вимірників, вимірах, фізичних, оптимального, величин, керування, спосіб
Код посилання
<a href="https://ua.patents.su/6-45289-rekurentnijj-sposib-optimalnogo-keruvannya-kompleksuvannyam-vimirnikiv-pri-nerivno-tochnikh-vimirakh-fizichnikh-velichin.html" target="_blank" rel="follow" title="База патентів України">Рекурентний спосіб оптимального керування комплексуванням вимірників при нерівно точних вимірах фізичних величин</a>
Попередній патент: Паралельний спосіб оптимального керування комплексуванням вимірників при нерівно точних вимірах фізичних величин
Наступний патент: Пристрій для виявлення дефектних тепловиділяючих зборок реактора
Випадковий патент: Гра у лайтбол