Паралельний спосіб оптимального керування комплексуванням вимірників при нерівно точних вимірах фізичних величин
Номер патенту: 45288
Опубліковано: 10.11.2009
Автори: Ігнатов Володимир Олексійович, Конахович Георгій Филимонович, Кудренко Станіслава Олексіївна, Нікулін В'ячеслав Ігорович
Формула / Реферат
Паралельний спосіб оптимального керування комплексуванням вимірників при нерівно точних вимірах фізичних величин, у якому для вимірювання значення фізичної величини паралельно застосовують декілька вимірювальних систем з різними погрішностями вимірювань, результати вимірювань запам'ятовують і по них за допомогою формул непрямих вимірювань обчислюють істинне значення фізичної величини, який відрізняється тим, що вагові коефіцієнти результатів вимірювань різними системами оптимально оцінюють за апріорно відомими дисперсіями погрішностей вимірювальних систем за формулою непрямих вимірювань:
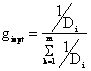 , i = 1, m,
, i = 1, m,
де ![]() - оптимальний коефіцієнт і-го вимірювання,
- оптимальний коефіцієнт і-го вимірювання,
Di - дисперсія погрішності вимірювання і-ою системою,
M - загальне число вимірювальних систем,
оптимальну комплексну оцінку Хорt результату вимірювань отримують за формулою непрямих вимірювань:
![]() ,
,
де ![]() - оптимальна комплексна оцінка результату вимірювань,
- оптимальна комплексна оцінка результату вимірювань,
![]() - результат і-го вимірювання,
- результат і-го вимірювання,
мінімальне значення дисперсії Dmin оптимальної оцінки Хорt отримують за формулою непрямих вимірювань:
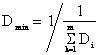 ,
,
середнє квадратичне значення ![]() оптимальної комплексної оцінки Хорt отримують за формулою непрямих вимірювань:
оптимальної комплексної оцінки Хорt отримують за формулою непрямих вимірювань:
![]() ,
,
мінімальне значення коефіцієнта варіації Vmin оптимальної комплексної оцінки Хорt отримують за формулою непрямих вимірювань:
![]() ,
,
індексний показник W1 порівняльної ефективності оптимального комплексного результату оцінювання відносно найменш точного вимірника отримують за формулою непрямих вимірювань:
![]() ,
,
індексний показник W2 порівняльної ефективності оптимального комплексного результату оцінювання відносно найбільш точного вимірника отримують за формулою непрямих вимірювань:
![]() ,
,
індексний показник W3 порівняльної ефективності оптимального комплексного результату оцінювання відносно середньої арифметичної оцінки, при отриманні якої всі вагові коефіцієнти вибирають однаковими і рівними 1/m, отримують за формулою непрямих вимірювань:
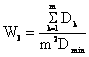 .
.
Текст
Паралельний спосіб оптимального керування комплексуванням вимірників при нерівно точних вимірах фізичних величин, у якому для вимірювання значення фізичної величини паралельно застосовують декілька вимірювальних систем з різними погрішностями вимірювань, результати вимірювань запам'ятовують і по них за допомогою формул непрямих вимірювань обчислюють істинне значення фізичної величини, який відрізняється тим, що вагові коефіцієнти результатів вимірювань різними системами оптимально оцінюють за апріорно відомими дисперсіями погрішностей вимірювальних систем за формулою непрямих вимірювань: 2 . 3 45288 Корисна модель відноситься до вимірювальної техніки і стосується непрямих вимірювань фізичних величин, в тому числі і радіотехнічними системами, для загального випадку вимірювань місцезнаходження, напрямів, відстаней, рівнів, азимутів у навігації, коли з метою підвищення точності та вірогідності для вимірювання одного і того ж значення фізичної величини використовують декілька вимірювальних систем, що мають різні значення погрішностей вимірювань. Відомим є спосіб нерівне точних вимірів [1], у якому використовують нормальну міру h точності системи з т нерівно точних вимірів m h= 2 Σ g i (X 0 − X i )2 k =1 m −1 (1) , де gi - ваговий коефіцієнт i-го вимірювання, X0 - оцінка значення параметру, що вимірюється, Хі - і-те значення результату вимірювання, коефіцієнт gi знаходять з умови gi = h i2 h 2 , i = l, m, (2) де міра точності і-го вимірювання hi = 1 4 мірюють фізичну величину Х4 і обчислюють істинне значення фізичної величини по формулі непрямих вимірів Х0 = K1Y1 + K2Y2 + (K1 + K2) Y3 + Y4 де Y1, ... Y4 - результати вимірів у першомучетвертому тактах, відповідно. В основу корисної моделі поставлено задачу оптимального визначення вагових коефіцієнтів в формулі непрямих вимірювань (5) за критерієм мінімуму дисперсії погрішності результату вимірювань Х0 шляхом розв'язання системи рівнянь оптимізації значень вагових коефіцієнтів і з урахуванням умови несміщеності оптимальної оцінки. Підвищення точності результату непрямих вимірювань значення фізичної величини досягається тим, що в способі виміру фізичних величин за А.С. СРСР № 1824589 [3] не послідовно, а паралельно роблять т вимірювань Yl, Ym різними вимірниками фізичної величини Х, Yi = kiX + ξі, і = l,m, 2D[Xi ] , a D[Xi] - дисперсія і-го вимірювання; Oцінку Х0 отримують по формулі непрямих вимірів (6) де ki є коефіцієнт передачі i-го перетворювача X в Yi при вимірюванні, ξі є випадкова погрішність i-го вимірника, що має гаусовський розподіл з математичним очікуванням і дисперсією. M[ξі] = 0, D[ξі] = Di, (3) (5) (7) результати вимірювань Yl, Ym для подальшої обробки запам'ятовують, за допомогою формули (8) непрямих вимірювань за апріорно відомими дисперсіями Dl, Dm погрішностей вимірників розраховують оптимальні значення вагових коефіцієнтів glopt, gmopt, m X0 = Σ g iopt Yi k =1 m Σ g iopt k =1 (4) , Недоліком способу є неможливість вибору hi, коли самі gi невідомі. Відомий також спосіб непрямого виміру фізичної величини шляхом послідовної тактової обробки результатів нерівне точних вимірів [2]. Цей спосіб не вимагає запам'ятовування всієї сукупності Yl, Ym, значень, що вимірюються, спрощує процедуру обробки і дозволяє обробити результати нерівне точних вимірів у реальному масштабі часу. Але як і перший спосіб, цей спосіб не вказує, як необхідно вибирати вагові коефіцієнти. Ці два способи розглядають як аналоги пропонованого способу. Прототипом корисної моделі служить спосіб виміру фізичних величин за авторським посвідченням СРСР № 1824589 [3]. ВІН полягає в тому, що в першому такті вимірюють фізичну величину X1 посилену (ослаблену) у K1 раз, у другому такті вимірюють фізичну величину Х2 посилену (ослаблену) у K2 разів, у третьому такті вимірюють фізичну величину Х3 посилену (ослаблену) у K1 + K2 разів, у четвертому такті ви 1 g iopt = m Di Σ 1 k =1 (8) Di , i = l,m, отримані оптимальні значення вагових коефіцієнтів використовують в формулах непрямих вимірювань (9) - (15) для визначення оптимальної комплексної оцінки (9) Хорt, фізичної величини Х, m X opt = Σ g iopt Yi k =1 , (9) мінімального значення дисперсії Dmin (10) оптимальної комплексної оцінки Хорt, D min = 1 1 m Σ Di k =1 (10) , середнього квадратичного значення (11) оптимальної комплексної оцінки Хорt, 5 σmin = Dmin , 45288 (11) мінімального значення коефіцієнту варіації (12) оптимальної комплексної оцінки Хорt, Vmin = σ min X opt (12) , індексних показників W1, W2, W3 порівняльної ефективності оптимального комплексного результату оцінювання відносно найменш точного вимірника W1 (13) (мажоранта паралельного гетерогенного способу вимірювань), W1 = D1 D min , (13) відносно найбільш точного вимірника W3 (14), W2 = Dm D min (14) відносно середньої арифметичної оцінки W2 (15), (міноранта паралельного гетерогенного способу вимірювань), при отриманні якої всі вагові коефіцієнти обирають однаковими i рівними l/m, m W2 = Σ Dk k =1 2 (15) m D min , На фіг. 1 показана узагальнена структурна схема способу. Спосіб реалізується наступним чином. Цикл вимірювань починається з того, що з об'єкту вимірювання OВ (блок 1) за сигналами управління СУ блока 2 управління та синхронізації БУС з бази даних БД 3 на блок 4 паралельної обробки БПО результатів прямих вимірювань паралельно (одночасно) подаються сигнали Dl, Dm, що відображають апріорні значення дисперсій погрішностей вимірників і сигнал X, який відображає вимірювану фізичну величину. БПО за командою БУС виконує операції вимірювання і запам'ятовування результатів вимірювання Yl, Ym, а також значень сигналів Dl, Dm. За наступною командою БУС БПО виконує обчислення за формулами непрямих вимірювань (8) - (12), що в даному випадку відіграють роль операторних рівнянь роботи певних функціональних пристроїв оптимального вимірювача. Після закінчення обчислень БПО за останньою командою БУС подає результати обчислень у вигляді сигналів Хорt σmin, Vmin, W1, W2, W3 на блок 5 відображення результатів вимірювань БВР у даному циклі. БВР відображає результати вимірювань. 6 Якщо обчислення виконують у цифровій формі, у структуру оптимального обчислювача включають аналоге - цифрові та цифро - аналогові перетворювачі вхідних та вихідних сигналів. Як випливає з принципу роботи структурної схеми способу, в способі вхідні сигнали Хто, Dl, Dm згідно операторних рівнянь (8) - (17) перетворюють у вихідні сигнали Хорt σmin, Vmin, W1, W2, W3. Тому цей спосіб можна назвати паралельним гетерогенним способом вимірювань, який дозволяє оптимально управляти комплексуванням т нерівне точних вимірювальних систем. Приклад 1. В цьому прикладі розглянуто результати експерименту, що був проведений методом статистичного імітаційного моделювання способу. Виконувалося оптимальне управління комплексуванням m = 5 нерівне точних вимірювальних систем. В ролі еталону був обраний детермінований параметр Х = 1. Дисперсії погрішностей вимірювальних систем було апроксимовано арифметичною прогресію Di = Dl - (i - l) d, i =l, m, (16) де параметри прогресії мали значення Dl = 0.04, d = 0.005. Для моделювання результатів вимірювань прийнято припущення, що усі ki= l, і = l, m, (17) а результати вимірювань моделюються реалізаціями випадкових величин за допомогою функції (18) системи MathCAD Yi = rnorm{n, M[X], σi}, і = l, m, (18) де число реалізацій вибрано n = l, математичне сподівання М[Х] = Х = l, середня квадратична погрішність σi = Di . Для моделювання роботи структурної схеми способу була розроблена програма ПГС - m/m0. Вона дозволяє використовувати різні вхідні дані експериментів і виконувати статистичні експерименти при різних обсягах виборок n і числі систем m < m0 в паралельному гетерогенному способі з характеристичним числом m0. В експерименті були обрані m = 5, m0 = 9. Реалізації Yi, утворювались за допомогою функції генерації випадкових чисел (18) з гаусовським розподілом при заданих n, M[X], σi. В експерименті була задана точність моделювання «шість знаків після коми». В результаті однократного використання операції (18) були отримані такі реалізації вимірювань: Y1 - 1.037235, Y2 = 0.838513, Y3 = 1.366219, Y4 = 0.804573, Y1 = 1.076496. В таблиці показано результати експерименту в одному конкретному експерименті. 7 45288 8 Таблиця. Результати експерименту ВР 1 2 Xopt X0 1 2 1.025618 1.024607 σmin σ0 V1, % V5, % 3 4 5 6 0.075185 0.07746 19.525 13.802 Аналіз результатів експерименту показує роботоздатність способу за схемою фіг. 1. Фіг. 2 ілюструє порівняльну ефективність способу. За результатами експериментів можна зробити висновок про те, що застосування паралельного гетерогенного способу забезпечує суттєве підвищення точності непрямих вимірювань. Числові значення показників ефективності змінюються від експерименту до експерименту, але оптимальна оцінка носить асимптотичне ефективний характер - з ростом числа експериментів все більше проявляється закономірність того, що ця оцінка забезпечує потенційну точність вимірювань. Приклад 2. Розглянемо застосування способу в системі автоматизованого керування повітряним рухом, а саме при оптимальному комплексуванні первинних і вторинних радіолокаторів при вимірі висоти польоту літаків як об’єктів керування. Врахуємо наступні вхідні дані. Середня квадратична погрішність виміру дальності R трасовими радіолокаторами на висотах польоту Н = (10-20)км становить приблизно σR = (0,2-0,25)км. Середня квадратична погрішність σH2 передачі висоти Н відповідачами вторинних радіолокаторів за показниками пілотажних приладів літаків становить приблизно σH2 ≈ 37,5м. Виконаємо за цим даними оптимальне комплексування й оцінимо його ефективність по формулах (13) - (15). Для визначення середньої квадратичної погрішності виміру висоти польоту літаків трасовими радіолокаторами врахуємо, що між дальністю дії R і висотою H польоту літаків існує залежність H = R sin[arctg(H / R 2 − H 2 )] = R sin β , (19) При R = 400км, Н = 10км, tg(10/400) ≈ 0,25, β ≈ 14°, sin14° ≈ 0,2419. Застосовуючи лінійну апроксимацію (19) для оцінки середньої квадратичної погрішності виміру висоти трасовими радіолокаторами одержимо σH 2 = 0,24192 × 2502 ≈ 60,475м . 2 2 У такий спосіб: DH1 ≈ 3657м , DH2 ≈ 1406,25м , U = DH1/ DH2 ≈ 2,6, gopt ≈ 0,72226, l-gopt ≈ 0,27774, D2min ≈ 0,72226 × 1406,25 ≈ 0,27774 × 3657 ≈ 2 1015,82м , σ2min ≈ 31,87м, W1(2,6) ≈ 3,6, W2(2,6) ≈ 1,38461, W3(2,6) ≈ 1,24615. Звідси випливає, що в порівнянні зі середньою арифметичною оцінкою оптимальне комплексування дозволяє приблизно на 25% зменшити дисперсію радіолокаційних вимірів висоти польоту, що є особливо актуальним при зменшенні діапазонів Vmin, % V0, % W1 W2 W3 7 7.331 8 7.569 9 2.663 10 1.883 11 1.031 ешелонування й використанні принципу «free flight». Приклад 3. Розглянемо особливості оптимального комплексування систем GPS і INS [4]. Для GPS середня квадратична погрішність доплеровського вимірника швидкості σν2 ≈ 0,09 m/s. Для INS середня квадратична погрішність автономного вимірника швидкості σν1 ≈ 1,03 m/s за одну годину польоту. Визначимо ефективність оптимального комплексування GPS і INS по виміру швидкості. Розрахуємо безрозмірний параметр U i вагові коефіцієнти (8) оцінки (9): 2 2 2 2 U = σν1 /σν2 = 1.03 /0,09 ≈ 130,975 gopt = 2 2 2 2 σν2 /(σν1 + σν2 ) = 0,0081 /(1,032 + 0,092) = 0,0075772, 1-gopt = 0,9924228. Визначимо значення D2min, σ2min і показників ефективності W1 – W3: D2min ≈ gopt σν12 ≈ 0,0075772 1,0609 ≈ 0,9924228 0,0081 ≈ 0,00803862468. σ2min = 0,0896584 m/s. W1 = l + U = 1 + 130,975 2 2 = 131,975. W2 = (1 + U) /4U = (1 + 130,975) /4 130,975 = 33,246. W3 = 1 + 1/U = 1+1/130,975 = 1,007635. 2 Розрахуємо внесок σν1 у загальну мінімальну дисперсію D20: ∆D1 = gopt2 D1 ≈ (0,0075772)2 0,0081 ≈ 0,00006137532. Визначимо відносну погрішність методу заміщення: ∆ = ∆D1/D20 ≈ 0,00006137532/0,00803862468 ≈ 0,007635 ≈ 0,7635 %. Результати розрахунків дозволяють зробити однозначний висновок про те, що при виконанні польотів в зоні дії GPS найбільш ефективним є використання методу заміщення. Він приводить до відносної середньої квадратичної погрішності, меншої 0,7635%. Інакше кажучи, результати вимірів INS доцільно корегувати за результатами супутникових вимірів GPS, які можуть розглядатися як еталонні результати, приблизно через щогодини польоту. Наведені результати експерименту і приклади наочно iлюструють новизну, корисність i ефективність способу, що пропонується. Список використаних джерел 1. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. М.: Физматгиз. - 1962.- 356 с. 2. Greenspan, R., L., "GPS/Inertial Overview", Aerospace Navigation Systems, AGARD - AG - 331, Advisory Group for Aerospace Research and Development, Neuilly - sur - Seine, France, June 1995. 3. A.c. СССР № 1824589. Способ измерения физических величин / Игнатов В.А. и др. 9 45288 10 4. Richard E. Phillips and George T. Schmidt LS - 207, Advisory Group for Aerospace Research "GPS/INS Integration", System Implications and Innoand Development, Neuilly - sur - Seine, France, June vative Applications of Satellite Navigation, AGARD 1996. Комп’ютерна верстка М. Мацело Підписне Тираж 28 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюParallel method for optimal control of complexation of measuring devices at varying-accuracy measurements of physical values
Автори англійськоюIhnatov Volodymyr Oleksiiovych, Konakhovych Heorhii Filimonovych, Kudrenko Stanislava Oleksiivna, Nikulin Viacheslav Igorovych
Назва патенту російськоюПараллельный способ оптимального управления комплексированием измерителей при неравноточных измерениях физических величин
Автори російськоюИгнатов Владимир Алексеевич, Конахович Георгий Филимонович, Кудренко Станислава Алексеевна, Никулин Вячеслав Игоревич
МПК / Мітки
МПК: G01C 3/00
Мітки: вимірників, фізичних, точних, комплексуванням, величин, спосіб, нерівної, оптимального, вимірах, паралельний, керування
Код посилання
<a href="https://ua.patents.su/5-45288-paralelnijj-sposib-optimalnogo-keruvannya-kompleksuvannyam-vimirnikiv-pri-nerivno-tochnikh-vimirakh-fizichnikh-velichin.html" target="_blank" rel="follow" title="База патентів України">Паралельний спосіб оптимального керування комплексуванням вимірників при нерівно точних вимірах фізичних величин</a>
Попередній патент: Спосіб визначення структури порового простору ґрунтів (дисперсних середовищ)
Наступний патент: Рекурентний спосіб оптимального керування комплексуванням вимірників при нерівно точних вимірах фізичних величин
Випадковий патент: Пристрій для транспортування і очистки коренебульбоплодів









