Спосіб двоетапного пошуку векторів під час ущільнення мовних векторів
Формула / Реферат
Спосіб двоетапного пошуку векторів під час ущільнення мовних сигналів, в якому простір векторів кодової книги розбивають на підобласті на основі бінарного дерева, здійснюють пошук вектора кодової книги, найближчого до вхідного за евклідовою метрикою згідно з формулою:
![]() ,
,
де ![]() - вхідний вектор;
- вхідний вектор;
![]() - i-й вектор кодової книги розмірності
- i-й вектор кодової книги розмірності ![]() ;
;
![]() - кількість векторів у кодовій книзі,
- кількість векторів у кодовій книзі,
причому під час прямого пошуку фіксують всі відстані до вузлів, обчислюють відстань до листа, якому належить вхідний вектор ![]() , після цього на зворотній фазі пошуку обчислюють відстані до тих листів дерева, для яких
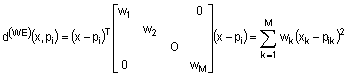
, після цього на зворотній фазі пошуку обчислюють відстані до тих листів дерева, для яких ![]() і визначають вектор кодової книги, що є найближчим до вхідного, який відрізняється тим, що за евклідовою метрикою знаходять не один найближчий вектор кодової книги, а множину кандидатів на найближчий вектор, впорядкованих за зростанням відстані до вхідного, з числа яких на другому етапі за зваженою евклідовою метрикою за формулою:
і визначають вектор кодової книги, що є найближчим до вхідного, який відрізняється тим, що за евклідовою метрикою знаходять не один найближчий вектор кодової книги, а множину кандидатів на найближчий вектор, впорядкованих за зростанням відстані до вхідного, з числа яких на другому етапі за зваженою евклідовою метрикою за формулою:
 ,
,
де ![]() - k-й ваговий коефіцієнт, який обчислюють на основі
- k-й ваговий коефіцієнт, який обчислюють на основі ![]() , вибирають один вектор, найближчий до вхідного.
, вибирають один вектор, найближчий до вхідного.
Текст
Реферат: Спосіб двоетапного пошуку векторів під час ущільнення мовних сигналів, в якому простір векторів кодової книги розбивають на підобласті на основі бінарного дерева, здійснюють пошук вектора кодової книги, найближчого до вхідного за евклідовою метрикою згідно з формулою: dE x, pi xi piM 2 , де x x1, x2,, xM - вхідний вектор; pi pi1, pi2,K, piM - i-й вектор кодової книги розмірності M ; n - кількість векторів у кодовій книзі, причому під час прямого пошуку фіксують всі відстані до вузлів, обчислюють відстань до листа, якому належить вхідний вектор Dmin , після цього на зворотній фазі пошуку обчислюють відстані до тих листів дерева, для яких Dk Dmin і визначають вектор кодової книги, що є найближчим до вхідного. За евклідовою метрикою знаходять не один найближчий вектор кодової книги, а множину кандидатів на найближчий вектор. UA 70762 U (54) СПОСІБ ДВОЕТАПНОГО ПОШУКУ ВЕКТОРІВ ПІД ЧАС УЩІЛЬНЕННЯ МОВНИХ ВЕКТОРІВ UA 70762 U UA 70762 U 5 10 15 20 25 30 35 Корисна модель належить до галузі обчислювальної техніки, а саме: ущільнення мовних сигналів і може бути використана в засобах запису, відтворення та передачі мовних сигналів, ідентифікації диктора та при розпізнаванні мови. Аналогом даного способу є "Спосіб спрямованого пошуку векторів при ущільненні мовних сигналів" [патент України на корисну модель № 48138, опублікований 10.03.10, бюлетень № 5/2010], в якому для прискорення пошуку найближчого вектора було розроблено спосіб структуризації кодових книг (КК) на основі діаграми Вороного та теорії мажоризації, який полягає у формуванні таблиць суміжності на основі діаграми Вороного, попередньо впорядкованих за рівнями мажоризації їх відстаней, обчисленні відстані від вхідного вектора до поточного, її порівняння з відстанями між вхідним вектором і таблицею суміжності поточного. При пошуку спочатку визначають рівень мажоризації, якому належить вхідний вектор та, починаючи з цього рівня, виконують пошук найближчого до нього вектора. Недоліком даного способу є великі матеріальні витрати, пов'язані з необхідністю виконання на підготовчому етапі значної кількості обчислень, необхідної для створення таблиць суміжності, а також збільшення обсягів пам'яті, потрібної для їх зберігання. За прототип вибрано спосіб [стаття Ткаченко О. М., Грійо-Тукало О. Ф. Пошук векторів у кодових книгах при ущільненні мовлення на основі бінарного дерева / О. М. Ткаченко, О. Ф. Грійо-Тукало // Інформаційні технології та комп'ютерна інженерія: 2011. - № 1. - С. 38-44], в якому спосіб здійснюють таким чином: простір векторів кодової книги розбивають на підобласті на основі бінарного дерева (БД). Щоразу при надходженні вхідного вектора по отриманому бінарному дереву здійснюють пошук найближчого до нього вектора кодової книги, причому відстані обчислюють за евклідовою метрикою згідно з формулою: dE x, pi xi piM 2 , де x x1, x2,, xM - вхідний вектор; pi pi1, pi2,K, piM - i-й вектор КК розмірності M ; n - кількість векторів у КК. Розрізняють дві фази пошуку - пряму та зворотну. Під час прямого пошуку фіксують всі відстані до вузлів бінарного дерева. Пряму фазу пошуку завершують p обчисленням відстані до листа БД, якому належить вхідний вектор Dmin . Після цього починають зворотну фазу пошуку, при цьому обчислюють відстані Dk лише до тих листів дерева, які можуть забезпечити виконання Dk Dmin . Якщо ця умова виконується, вважають Dmin Dk . В результаті знаходять вектор кодової книги, що є найближчим до вхідного. Крім того, якщо погодитись з тим, що знайдений вектор не обов'язково найближчий за евклідовою метрикою, але є досить близьким (з певною похибкою e 0 ), пошук можна ще прискорити. Вектор кодової книги є 1 e найближчим вектором до x , якщо виконується: dx, p 40 45 d x, p ; p, p Q, e 0 , 1 e де p - найближчий вектор КК, знайдений до цього моменту. Пошук 1 e - найближчого вектора здійснюється таким чином: спочатку визначають лист, якому належить вхідний вектор, спускаючись по дереву (на прямій стадії пошуку), після цього здійснюють запам'ятовування листових вузлів у черзі в порядку збільшення відстані до x та визначають відстань до векторів КК, що відповідають листам. Як тільки відстань від x до поточного листа відповідає умові, наведеній вище, пошук зупиняють. Якщо задати e 0 , здійснюють пошук дійсно найближчих векторів. Недоліком описаного способу є те, що він, як і інші методи швидкого пошуку, не дозволяє застосовувати для пошуку найближчого сусіда зважену евклідову метрику dWE : 0 w1 M w2 x p dWE x, pi x pi T w k xk pik 2 , i O k 1 wM 0 оскільки вагові коефіцієнти w k обчислюють на основі вхідного вектора, який надходить в 50 режимі реального часу. Застосування ж простої евклідової метрики під час швидкого пошуку призводить до втрати продуктивності, що виражається у збільшенні спектрального спотворення. Тобто, оскільки за зваженою евклідовою метрикою різні розмірності мають різну вагу, вектор 1 UA 70762 U 5 10 15 20 25 30 кодової книги, що є найближчим за евклідовою метрикою, може виявитися не найкращим кандидатом при врахуванні ваг. В основу корисної моделі поставлено задачу створення способу двоетапного пошуку векторів під час ущільнення мовних сигналів, в якому за рахунок поєднання швидкого пошуку із застосуванням зваженої евклідової метрики (яка дозволяє отримати менше спектральне спотворення SD) досягають виграшу в швидкодії при збереженні мінімально можливого спектрального спотворення, що в результаті приводить до зменшення складності обчислень без втрати якості відтворення синтезованого звуку. Поставлена задача вирішується тим, що в способі двоетапного пошуку векторів під час ущільнення мовних сигналів простір векторів кодової книги розбивають на підобласті на основі бінарного дерева, здійснюють пошук вектора кодової книги, найближчого до вхідного за евклідовою метрикою згідно з формулою: dE x, pi xi piM 2 , де x x1, x2,, xM - вхідний вектор; pi pi1, pi2,K, piM - i-й вектор кодової книги розмірності M ; n - кількість векторів у кодовій книзі, причому під час прямого пошуку фіксують всі відстані до вузлів, обчислюють відстань до листа, якому належить вхідний вектор Dmin , після цього на зворотній фазі пошуку обчислюють відстані до тих листів дерева, для найближчим до вхідного, при цьому вектор кодової книги, а множину зростанням відстані до вхідного, з метрикою за формулою: яких Dk Dmin і визначають вектор кодової книги, що є за евклідовою метрикою знаходять не один найближчий кандидатів на найближчий вектор, впорядкованих за числа яких на другому етапі за зваженою евклідовою 0 w1 M w2 x p dWE x, pi x pi T w k xk pik 2 , i O k 1 wM 0 де w k - k-й ваговий коефіцієнт, який обчислюють на основі x , вибирають один вектор, найближчий до вхідного. На кресленні наведено схему пошуку, яка пояснює спосіб вибору найближчого вектора з кодової книги, впорядкованої на основі бінарного дерева для двовимірного випадку. Спосіб здійснюють таким чином: кодова книга містить кінцеву множину векторів Q p1, p2,K, pn , pi pi1, pi2,K, piM . Таким чином, з кожним вектором p j у КК пов'язаний індекс або кодове слово j , що може бути записано як n-розрядне ціле число. На вхід квантизатора надходить вектор x x1, x2,, xM . В результаті кодування необхідно вибрати таке кодове слово j , що мінімізує спотворення dx, p j (правило вибору найближчого сусіднього вектора). R j x : d x, p j dx, pi ; i I, i j , 35 40 де I ,2,K, n - множина індексів. 1 Простір векторів кодової книги розбивають на підобласті на основі бінарного дерева. Бінарне дерево має два типи вершин: листи та вузли, причому кожен лист дерева може містити не більше одного вектора кодової книги Yi , тобто lк Yi або lк , де lк - деякий лист БД. Щоразу при надходженні вхідного вектора по отриманому бінарному дереву здійснюють пошук вектора кодової книги, найближчого до вхідного за евклідовою метрикою згідно з формулою: dE x, pi xi piM 2 , де x x1, x2,, xM - вхідний вектор; pi pi1, pi2,K, piM - i-й вектор кодової книги розмірності M ; 45 n - кількість векторів у кодовій книзі, Під час прямого пошуку фіксують всі відстані до вузлів дерева di . Пряму фазу пошуку завершують обчисленням відстані до листа, якому належить вхідний вектор Dk Dmin . Після цього починають зворотну фазу пошуку, при цьому обчислюють відстані Dk лише до тих листів дерева, які можуть забезпечити виконання Dk Dmin . Якщо ця умова виконується, вважають 50 Dmin Dk . В результаті знаходять вектор кодової книги, що є найближчим до вхідного. 2 UA 70762 U При цьому за евклідовою метрикою знаходять не один найближчий вектор кодової книги, а множину кандидатів на найближчий вектор, впорядкованих за зростанням відстані до вхідного: C Q p1, p2, K, pt , t n, C t 5 10 де C - потужність множини C . Це можливо за рахунок того, що дані про відстань до вже пройдених листів зберігаються і одночасно здійснюється їх впорядкування за зростанням відстані від вхідного вектора. Завдяки цьому додаткове знаходження декількох найближчих векторів не потребує багато часу. Таким чином, на першому етапі з кодової книги, впорядкованої на основі бінарного дерева, за евклідовою метрикою відбирають C найближчих векторів кодової книги, впорядкованих за зростанням відстані, до вхідного вектора. Суть другого етапу полягає в тому, що використовуючи зважену евклідову метрику, з множини кандидатів на найближчий до вхідного вектор кодової книги C за формулою: 0 w1 M w2 x p dWE x, pi x pi T w k xk pik 2 , i O k 1 wM 0 де w k - k-й ваговий коефіцієнт, який обчислюють на основі x , 15 вибирають один вектор, найближчий до вхідного. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 20 25 30 Спосіб двоетапного пошуку векторів під час ущільнення мовних сигналів, в якому простір векторів кодової книги розбивають на підобласті на основі бінарного дерева, здійснюють пошук вектора кодової книги, найближчого до вхідного за евклідовою метрикою згідно з формулою: dE x, pi xi piM 2 , де x x1, x2,, xM - вхідний вектор; pi pi1, pi2,K, piM - i-й вектор кодової книги розмірності M ; n - кількість векторів у кодовій книзі, причому під час прямого пошуку фіксують всі відстані до вузлів, обчислюють відстань до листа, якому належить вхідний вектор Dmin , після цього на зворотній фазі пошуку обчислюють відстані до тих листів дерева, для яких Dk Dmin і визначають вектор кодової книги, що є найближчим до вхідного, який відрізняється тим, що за евклідовою метрикою знаходять не один найближчий вектор кодової книги, а множину кандидатів на найближчий вектор, впорядкованих за зростанням відстані до вхідного, з числа яких на другому етапі за зваженою евклідовою метрикою за формулою: 0 w1 M w2 x p dWE x, pi x pi T w k xk pik 2 , i O k 1 wM 0 35 де w k - k-й ваговий коефіцієнт, який обчислюють на основі x , вибирають один вектор, найближчий до вхідного. 3 UA 70762 U Комп’ютерна верстка А. Крижанівський Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for two-stage search of vectors during compression of speech signals
Автори англійськоюVINNYTSIA NATIONAL TECHNICAL UNIVERSITY
Назва патенту російськоюСпособ двухэтапного поиска векторов во время уплотнения речевых векторов
Автори російськоюВИННИЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
МПК / Мітки
МПК: G10L 19/00, G10L 21/00
Мітки: ущільнення, векторів, двоетапного, мовних, спосіб, пошуку
Код посилання
<a href="https://ua.patents.su/6-70762-sposib-dvoetapnogo-poshuku-vektoriv-pid-chas-ushhilnennya-movnikh-vektoriv.html" target="_blank" rel="follow" title="База патентів України">Спосіб двоетапного пошуку векторів під час ущільнення мовних векторів</a>
Попередній патент: Спосіб лікування патологічної тяги до алкоголю в терапії синдрому відміни при алкогольній залежності
Наступний патент: Пристрій для вібраційної обробки внутрішніх поверхонь трубчастих виробів
Випадковий патент: Шпиндельний вузол верстата










