Гіротеодоліт

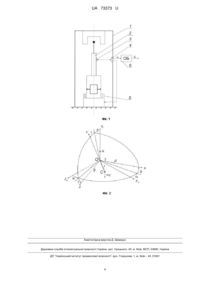
Реферат: UA 73373 U UA 73373 U 5 10 15 20 25 Корисна модель належить до галузі прецизійного приладобудування і може бути використана для визначення орієнтації об'єктів на поверхні Землі, зокрема при вирішенні задач у галузі геодезії та будівництва. При роботі гіротеодоліту в умовах поступальних та кутових коливань основи виникає додаткова вібраційна похибка приладу. В роботі [1] досліджувалась така похибка та засоби підвищення точності гіроскопічних засобів орієнтації в умовах вібрації. Аналіз похибки дозволяє зробити висновок, що вібраційна похибка гіротеодоліту має той самий фізичний зміст, що й інтеркардинальна девіація гірокомпасів. В роботах [2, 3] показана можливість зменшення вказаної похибки, шляхом її аналітичного розрахунку і подальшої компенсації у вихідному сигналу гіротеодоліту. Найближчим аналогом корисної моделі гіротеодоліт (патент України № 75648 «Гіротеодоліт» від 15.05.2006). У відомому гіротеодоліті підвищення точності виконується шляхом використання додаткових конструктивних елементів, застосування яких дозволяє виключити деякі похибки приладу. В основу корисної моделі поставлено задачу підвищення точності гіротеодоліту. Поставлена задача вирішується тим, що в складі приладу додаткового міститься обчислювальний блок, який оброблює інформацію з датчика кута. На Фіг. 1 зображена функціональна схема гіротеодоліту. До складу входять корпус 1, чутливий елемент 2, дзеркало 3, фотоелектричний датчик кута 4, датчик моменту 5, обчислювальний блок 6. Гіроскопічний маятниковий чутливий елемент (ЧЕ) 2 з дзеркалом 3 підвішено всередині корпусу 1. На корпусі 1 закріплено фотоелектричний датчик кута 4, який за допомогою оптичного зв'язку з дзеркалом визначає кут відхилення чутливого елемента в азимуті. Датчик моменту 5 створює керуючий момент, який пропорційний сигналу з датчика кута і прикладається до ЧЕ. В обчислювальному блоці 6 відбувається визначення оцінки кутової швидкості чутливого елемента в азимуті за допомогою спостерігаючого пристрою. На Фіг. 2 зображено кінематику поворотів чутливого елемента. Математичну модель гіротеодоліту запишемо на основі рівнянь руху по координатах  і  [3]:    1. Jy   H  FКС  f   HЗ cos g 1  k     mgl  n X t     nZ t ;    2. Jz  H  f  mgl  mgl  n X t   HЗ sin g; 30 де k  (1) KКС ; nX t   nm cos  0  sin t; nZ t   nm sin  0  sin t - проекції перевантаження HЗ cos g точки підвісу гіротеодоліту H - кінетичний момент гіроскопа; m - маса чутливого елемента; l зміщення центру мас ЧЕ відносно точки підвісу; , ,  - кути повороту чутливого елемента відносно корпусу приладу; f , f, f - коефіцієнти в'язкого тертя; З - кутова швидкість обертання Землі;  g - географічна широта місця встановлення приладу; KКС - коефіцієнт компенсаційного 35 зв'язку; FКС - коефіцієнт демпфування, пропорційний коефіцієнту компенсаційного зв'язку. JY, JZ - моменти інерції чутливого елемента. Перепишемо систему рівнянь (1) в формі простору станів, позначивши змінні стану   x1  , x2  , x3  , x 4   :  X  AX  , (2)  Y  CX  40 де X - вектор стану, A - матриця стану, Y - вектор вимірювань, C - матриця вимірювань:  0  x1   k    J x2  X ; A y  x3   0    x 4     0  0  H 0   Jy  ; C  1 0 0 0. 0 1  f  mgl    Jz Jz  Отже, вектор вимірювань Y складається з одного елемента - вимірюваного кута  . 1 f  FКС  Jy 0 H Jz 0 Запишемо матрицю спостережуваності: 1 UA 73373 U  1   0  T T T T 2 T T 3 T  Q  C  A C  A C  A C       0   0       k  f  FКС     2 2   k     f  FКС   H   J Jy Jz  J2 y y  . mgl  H   Jy Jz  Hf  FКС    J2 y   k Jy 0  1  f  FКС Jy 0 0 J2 y 0  H Jy Ранг матриці спостережуваності рівний порядку об'єкта rankQ 4 , отже, за виміряним вектором Y можливо оцінити всі змінні стану об'єкта. Спостерігаючий пристрій, при відсутності збурень, описується рівнянням: 5 10 15 20  ˆ ˆ X  A  KCX  KY , (3) ˆ де X - вектор оцінок змінних стану, K - матриця коефіцієнтів спостерігаючого пристрою. ˆ  x1   k1  ˆ    k x2  ˆ X ; K   2 .  x3  k 3  ˆ     k 4  x 4    ˆ  Коефіцієнти матриці K вибираються таким чином, щоб власні значення спостерігача, що визначається рівнянням (3), знаходились в певних заздалегідь заданих точках на комплексній площині. Характеристичне рівняння спостерігача має вигляд: detpE  A  KC  0 ; (4) де E - одинична матриця, відповідної розмірності, p - оператор Лапласа. Таким чином, задача синтезу спостерігаючого пристрою зводиться до визначення матриці коефіцієнтів K . Оберемо біноміальний розподіл коренів характеристичного рівняння [4], тоді повинна виконуватись рівність: detpE  A  KC  p  0 4 ; (5) тобто характеристичне рівняння спостерігаючого пристрою буде мати один від'ємний дійсний корінь p  0 кратності 4. Підставляючи матриці A, K, E і C в ліву частину виразу (5) отримаємо:  FKC  f Jz  fJy  detpE  A  KC  p4    k1 p3    Jy Jz   2  FKC  f f  Jymgl  k  Jz  H  k1 FKC  f Jz  fJy    k 2 p2    Jy Jz       FKC  f mgl  k  f  k1FKC  f f  H2  Jymgl  k 2fJy  k 4JzH Jy Jz p k mgl  k1FKC  f mgl  k 2Jymgl  k 3H  mgl Jy Jz 2 4 Права частина виразу (5): p  0 4  p4  40p3  60p2  43p  0 . 0 Прирівнюючи коефіцієнти при рівних степенях р в лівій і правій частині виразу (5), можна визначити коефіцієнти матриці K : 2 UA 73373 U k1  40  FKC  f   f ; Jy 2 k 2  60  40 2 k 3  60 2 k 4  60 5 10 15 20 25 Jy H Jz FKC  f   FKC  f 2  40f  f2  FKC  f f  mgl  k   J2 y Jy  40 fJy JzH 4  0 Jz Jy H  mgl  J2 z Jy Jz Jz Jy H2 Jy Jz 2 H Jy f Jymgl  2  Jz JzH JzH 2 3  Jymgl Jy f    43 Jy  2fH  Jy f  2Jy fmgl  HFKC  f   40  H   0  H H JzH  H Jz JzH Jy J2H z   fJy Отже, при інтегруванні рівняння (3) зі знайденими значеннями коефіцієнтів матриці K , ˆ  отримаємо шукану оцінку кутової швидкості  . Таким чином, синтезований спостерігаючий пристрій виключає необхідність використання  спеціальних конструктивний засобів для визначення кутової швидкості  . Джерела інформації: 1. Лазарев Ю. Ф., Мироненко П. С, Литовко Г. В. О погрешностях гирокомпаса в компенсационном режиме при поступательной вибрации точки подвеса. \\ Вестник КПИ. Приборостроение, вып. 12. - Київ: КДУ, "Вища школа", 1982. - С. 26-28 2. Лазарев Ю. Ф., Мироненко П. С. Обобщенная форма представления систематической погрешности наземного гирокомпаса, обусловленной вибрацией. \\ Механика гироскопических систем. Республиканський міжвідомчий науково-технічний збірник, вип. 6. - Київ: КДУ, "Вища школа", 1987. 3. Мураховский С. А., Лазарев Ю. Ф., Мироненко П. С. Динамика наземного компенсационного маятникового гирокомпаса. \\ Вісник Інженерної академії України, вип. 2 Київ: 2010. - С. 125-130 4. Кузовков Н. Т. Модальное управление и наблюдающие устройства. - М.: Машиностроение, 1976. - 184 с. ФОРМУЛА КОРИСНОЇ МОДЕЛІ Гіротеодоліт, який містить корпус, всередині якого підвішений чутливий елемент, датчик кута, що визначає кут повороту чутливого елемента відносно корпуса в азимуті, та датчик моменту, що створює керуючий момент, який відрізняється тим, що гіротеодоліт додатково містить обчислювальний блок, вхід якого з'єднаний з виходом датчика кута, і в якому визначається оцінка кутової швидкості повороту чутливого елемента відносно корпуса. 3 UA 73373 U Комп’ютерна верстка Д. Шеверун Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4