Система захисту від дії куль, осколків снаряду на об’єкт

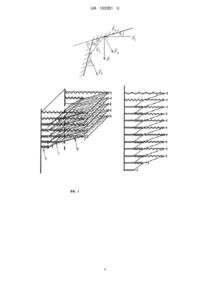
Реферат: Система захисту від дії куль, осколків снаряду на об'єкт при їх обстрілі зі стрілецької зброї та гармат калібру до 30 мм. Вона є багатошаровою моделлю, утвореною з бронелистів, зігнутих під кутом, більшим 100 градусів, що може бути використано як для створення броньованого захисту, так і для додаткових захисних екранів для техніки. UA 103351 U (54) СИСТЕМА ЗАХИСТУ ВІД ДІЇ КУЛЬ, ОСКОЛКІВ СНАРЯДУ НА ОБ'ЄКТ UA 103351 U UA 103351 U 5 10 15 20 25 30 35 40 Корисна модель належить до області машинобудування, зокрема до "елемента посиленого захисту". Її робота базується на принципі зміни кута атаки на поверхню одночасно зі зменшенням кінетичної енергії кулі (снаряду). Модель може бути використана як для створення броньованого захисту, так і для додаткових захисних екранів для техніки. Корисна модель призначена для вирішення завдань, пов'язаних з підвищенням живучості бойових броньованих машин (автомобілів з додатковим бронезахистом) при їх обстрілі зі стрілецької зброї та гармат калібру до 30 мм. У ній враховані вага пластин, пружність пружин між пластинами, вага та швидкість кулі, кут нахилу пластин до ймовірного напрямку швидкості кулі (осколка). Все це впливає на характеристики стійкості балістичного захисту бронемашини. На сьогодні є актуальним питання підвищення рівня захисту бойових броньованих машин (ББМ) без значного збільшення маси корпусу. Запропонована модель дозволяє захистити корпус ББМ в місцях, де листи зварного броньованого корпусу розміщені під кутом, близьким до 90 градусів до вектора взаємодії з кулею (снарядом). Також ця модель може бути застосована для підвищення захисту стаціонарних об'єктів у певних місцях. Існуючі моделі, наприклад, захисних екранів, не враховують напрямку швидкості кулі (снаряду), через що кут атаки кулі на ціль (бронелист або елемент екрана) виходить великий, що в свою чергу веде до зіткнення з ціллю та продовження руху кулі або стального сердечника майже без зміни вектора дії сили інерції. Також не враховується той факт, що при розміщенні бронелиста з меншим кутом до лінії атаки кулі збільшується шлях проходження кулі в листі, що веде до зменшення кінетичної енергії кулі. В основу корисної моделі поставлено задачу підвищити живучість (ББМ) чи додаткового броньованого захисту приміщень при їх обстрілі за допомогою використання моделі багатошарової системи (збірної конструкції), яка складається з листів, розміщених під кутом одна до одної, які через отвори з'єднані стержнем з обмежувачем з одного боку, а з іншого -з пружиною, кріпляться до стінки екрана. І так шар за шаром листів твердих і пружних матеріалів, які забезпечують зменшення кінетичної енергії куль та осколків снарядів, оскільки початкова кінетична енергія кулі витрачається на деформацію (руйнування) пластини та надання їй швидкості. Для зміни вектора руху кулі пропонується створити багатошарову модель з листами, зігнутими під кутом більшим 100 градусів. Суть запропонованої корисної моделі представлена на фіг. 1 (Збірна конструкція броні), фіг. 2 (Елементи збірної конструкції броні), де: 1 - стержень з обмежувачем руху 5, 2 - отвори крізь, які проходять стержні, 3,4 - пластини, розміщені одна до одної під кутом, 6,7,8 - пружини. Поставлена задача вирішується таким чином: Вищезазначена механічна система складається з набору зігнутих пластин 3,4 твердого матеріалу і отворів 2 у них, через які за допомогою стержнів 1 з пружинами 6,7,8 вони кріпляться до стінки з одного боку, а з іншого з допомогою обмежувача руху 5 тримаються на стержні 1. Розглядається задача удару кулі до нерухомої поверхні перешкоди з метою визначення максимально допустимої величини кута падіння кулі α1 на поверхню, в результаті чого куля буде відбиватись від поверхні перешкоди.  45 Для визначення гранично допустимої величини кута α1 між напрямком швидкості кулі V1 і поверхнею перешкоди використаємо теорему про зміну кількості руху матеріальної точки 50 перешкоди;    K 2  K1   St  , (1)     де K 2  mV2 - кількість руху матеріальної точки після відбиття від перешкоди; K 1  mV1 кількість руху матеріальної точки до удару об перешкоду; m - маса кулі, яка ударяється в   перешкоду; V1 - швидкість кулі до удару об перешкоду, V2 - швидкість кулі після відбиття від   St  - сума імпульсів всіх сил, які діють на кулю в проміжок її контакту з перешкодою.   Під час контакту кулі з перешкодою на неї діють: P - вага кулі; Fn - нормальна складова  реакції поверхні перешкоди, F - дотична складова реакції поверхні перешкоди. Отже імпульс цих сил дорівнює 55        St   P  Fn  F dt 1 , (2) 1 UA 103351 U де dt - елементарний проміжок часу, впродовж якого куля контактує з нерухомою поверхнею перешкоди. Підставляючи записані залежності в (1), запишемо, що 1        mV2  mV1  P  Fn  F dt 1 5 . (3) Проектуючи цю залежність на нормальний і тангенціальний напрямки поверхні перешкоди, отримаємо mV2 sin 1   mV1 sin 1   Fn  P cos 1 dt 1 ; (4) mV2 cos 1  mV1 cos 1   F  P sin 1 dt 1 , (5) 10 де 1 - кут, під яким куля вдаряється об нерухому поверхню перешкоди, 1 - кут, під яким куля відбивається від поверхні перешкоди. Враховуючи, що тривалість часу dt 1 контакту кулі з поверхнею перешкоди є малою величиною, а величини сил P та F є значно менші від величини сили Fn , систему рівнянь (4) і (5) перепишемо у вигляді mV2 sin 1  mV1 sin 1  Fn dt 1 ; (6) 15 20 mV2 cos 1  mV1 cos 1  0 . (7) Для визначення швидкості кулі V2 і кута 1 , під яким куля рухається після відбиття від поверхні перешкоди використаємо гіпотезу Ньютона: відношення модуля нормальної складової відносної швидкості між тілами після удару до модуля нормальної складової відносної швидкості між тілами до удару дорівнює коефіцієнту відновлення. Для нашого випадку математичний запис гіпотези Ньютона набуде вигляду V2 sin 1  k1 V1 sin 1 , (8) де k1 - коефіцієнт відновлення, величину якого визначають експериментальним шляхом і k1  1 . Враховуючи залежність (7) і (8) отримаємо, що 25 V2 cos 1  V1 cos 1 , V1 cos  1 V1 cos  1 sin 1  k1 cos 1 , V1 sin  1 cos 1 або tg1  k1tg1 . (9) V2  З рівняння (9) визначається величина кута 1 , під яким куля відбилась від поверхні перешкоди. Враховуючи (9) і те, що cos 1  30 1  1 1  tg21 , запишемо 1 2 1  k 1 tg2 1 . (10) З рівнянь (7) і (10) визначаємо швидкість кулі V2 після відбиття від поверхні перешкоди 2 V2  V1 cos 1 1 k1 tg21 . (11) Величину нормальної реакції Fn поверхні перешкоди визначаємо, використовуючи рівняння (6) і (8), тоді Fn  35 m1  k 1 V1 sin 1 dt . (12) Вважаємо, що куля відбивається від поверхні перешкоди, якщо величина нормальної реакції Fn поверхні перешкоди менша від величини сили опору R1опір матеріалу перешкоди, тобто Fn  R1опір . (13) Враховуючи (12) і (13), отримаємо співвідношення m1  k1 V1 sin 1  R1опір dt 1 , (14) 2 UA 103351 U з якого можна визначити максимальну величину кута 1max , при якому куля відбивається від поверхні перешкоди sin 1max  5 R1опір dt 1 m1  k1 V1 . (15) На другому етапі куля вдаряється об другу поверхню перешкоди під кутом  2 , який дорівнює  2    1 , (16) де  - кут між поверхнями перешкод. Використовуючи попередні результати можна стверджувати, якщо кут  2 , під яким куля вдаряється об другу перешкоди, менше граничної величини 10  2   2 max , (17) де  2 max визначають з нерівності sin  2 max  R 2опір dt 2 m1  k 2 V2 , (18) то вона відіб'ється від поверхні перешкоди. Тут позначено: R 2опір - величина сили опору матеріалу другої перешкоди, dt 2 - тривалість часу контакту між кулею і другою поверхнею 15 перешкод, k 2 - коефіцієнт відновлення для матеріалу другої перешкоди. Враховуючи залежність (16) отримаємо, що величину кута  між поверхнями перешкод визначаємо з рівняння sin  1   R 2опір dt m1  k 2 V2 , (19) або sin  1   20 R 2опір dt 2 2 m1  k 2 V1 cos 1 1  k 1 tg2 1 . (20) Розглянемо приклад визначення кутів нахилу 1max m  0,0096кг , V1  800 м і  поверхонь перешкод, якщо с , R1опір  20000н , dt 1  0,0001с , k1  0,5 , R 2опір  20000н , dt 2  0,00015с , k 2  0,5 . Здійснюючи математичні обчислення, отримаємо, що 1max  100 , 1  5 0 , V2  790 м с ,  2 max  150 , V3  770 м с ,   200 . 25 Аналізуючи наведене можемо стверджувати, що, пробиваючи рухому пластину захисного екрану, швидкість кулі суттєво зменшується. Запропонована модель дає можливість зменшити кінетичну енергію кулі та змінити її вектор падіння на інші листи, а в кінцевому результаті - і на поверхню броні об'єкту. 30 ФОРМУЛА КОРИСНОЇ МОДЕЛІ 35 Система захисту від дії куль, осколків снаряду на об'єкт, при їх обстрілі зі стрілецької зброї та гармат калібру до 30 мм, яка відрізняється тим, що є багатошаровою моделлю, утвореною з бронелистів, зігнутих під кутом, більшим 100 градусів. 3 UA 103351 U 4 UA 103351 U Комп’ютерна верстка І. Скворцова Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 5