Гіроскопічна система

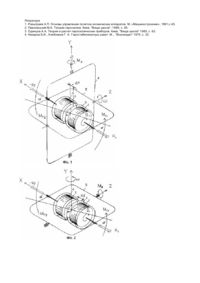
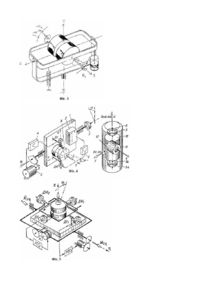
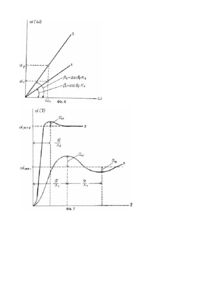
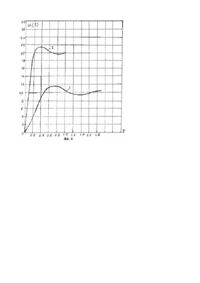
Винахід відноситься до галузі гіроскопії і може бути використаний для створення навігаційних систем орієнтації та стабілізації авіаційних і космічних апаратів. Відомо дво- і трьохосьові гіроскопі, які містять гіромотор, розміщений у кардановому підвісі [І]. Недоліками відомих гіроскопів є низькі чутливість відносно зовнішніх обурюючих моментів та швидкодія перехідних процесів. Відомо дво- і трьохосьові гіроскопи, які містять внутрішню та зовнішню рамки і гіромотор [2]. Недоліками відомих гіроскопів є низькі чутливість, яка визначається значенням кута повороту рамки гіроскопа відносно вісі прецесії та швидкодія перехідних процесів. Відома гіроскопічна система, яка містить два незалежних гіромотора з протилежним напрямом кінетичних моментів і періодичним реверсуванням обертання роторів гіромоторів [3]. Недоліками відомої гіроскопічної системи є низькі чутливість і швидкодія перехідних процесів кожного з відокремлених гіроскопів. Найбільш близькою до заявленої гіроскопічої системи (ГС) є ГС, що містить перший та другий гіромотори, розташовані несиметрично відносно центру карданового підвісу з протилежно направленими кінетичними моментами [4], що обрана як прототип. Недоліками відомого технічного рішення є низькі чутливість і швидкодія перехідних процесів. Задача запропонованого винаходу полягає в підвищенні чутливості, як функції кута прецесії від зовнішнього обурення та швидкодії перехідних процесів, як функції сталого кута прецесії від часу, а також зменшення перерегулювання. Поставлена задача вирішується тим, що в ГС, що містить перший та другий гіромотори закріплені в кардановому підвісі, новим є те, що гіромотори розташовані на одні осі і закріплені в центрі карданового підвісу. На фіг. 1 зображена схема трьохосьової гіроскопічної системи. На фіг. 2 подана схема двохосьової гіроскопічної системи. На фіг. 3 подана схема гіроскопічної системи, як вимірювача кутової швидкості. На фіг. 4 подана схема двохосьової системи стабілізації гіроплатформи з використанням бінарних промоторів. На фіг. 5 подана схема трьохосьової системи стабілізації гіроплатформи. На фіг. 6 представлені характеристики функцій чутливості. На фіг. 7 представлені теоретичні перехідні процеси. На фіг. 8 представлені динамічні процеси для розрахунків прикладів. Гіроскопічна система (фіг.1) містить перший гіромотор, який складається з ротора 1 і статора 2, другий гіромотор, який складається з ротора 3 і статора 4, та внутрішню рамку 5 і зовнішню рамку 6 карданового підвісу. Гіромотори розташовані на вісі Х таким чином, що відстань DX між ними дорівнює нулю, а центр бінарного гіромотора збігається з центром карданового підвісу 5,6, а кутові швидкості W 1 і W 2 обертання роторів 1 і 3 рівні і протилежно направлені. Така орієнтація бінарних промоторів дозволяє створити пару гіроскопічних моментів відносно вісі Z: Mг1 = Н1w cos a (1) - гіроскопічний момент 1 -го ротора, де: H1 - кінетичний момент 1-го ротора відносно вісі X; w - кутова швидкість обертання рамки 5 відносно вісі Z; a - кут відхилення рамки 5 навколо вісі прецесії і гіроскопічний момент 2-го ротора, Mг 2 = Н2 w cos a (2) де H 2 - кінетичний момент 2-го ротора. При виконанні умови H1 = H 2 з сумарний гіроскопічний момент, прикладений до рамки 5 буде дорівнювати: Mг = Мг1 + Мг 2 = Н1w cos a + H2 w cos a - 2Hw cos a (3) Функціонування пропонованої бінарної гіроскопічної системи (БГС) можна ілюструвати на прикладі діференціючої БГС (вимірювана кутової швидкості), фіг. 3. БГС складається з першого та другого роторів 1, 3, статора 2, рамки 5, датчика 7 кута повороту рамки 5, пружини 8, демпфера 9. Гіроскопічна система (ГС) на фіг. 3 відрізняється від ГС на фіг. 1 і 2 тим, що перший та другий ротори мають спільний статор 2. Моменти отру, які створюються пружиною 8 та демпфером 9 можуть бути представлені рівняннями: Mn = k n a (4) де k n - коефіцієнт жорсткості пружини. Mq = k q a (5) k де q - коефіцієнт демпферування Тоді рівняння руху відомого гіроскопа відповідає рівнянню: .. . I a + k q a + k n a = Hw cos a (6) де I - момент інерції рухомої частини ГС. Як правило, жорсткість пружини k n вибирається такою, що кут a мал во всьому діапазоні вимірювальних швидкостей. Отож, можна покласти cos a » 1 , тоді рівняння (6) буде мати вид: .. . I a + k q a+ k n a = H w (7) Тоді рівняння руху заявленого технічного рішення буде відповідати наступному виразу: .. . AI a+ k q a + k n a = BHw (8) де A - коефіцієнт визначення моменту інерції І; B - коефіцієнт визначення кінетичного моменту, наприклад: .. . 2I a+ k q a + k n a = 2Hw (9) Для такого типу датчиків та поплавкових гіроскопів стале значення відділення рамки 5 визначається значенням вимірюваної кутової швидкості H ac = w kn (10) Характеристика чутливості відповідно рівнянню (10) приведена на фіг. 4, поз. 1. Отже, для заявленої гіроскопічної системи характеристика чутливості має вид: 2H ac = w kn (11) і приведена на фіг. 4 поз. 2, що доказує підвищення чутливості БГС порівняно з прототипом. Динамічні характеристики однороторного гіроскопа визначаються його передаточною функцією: W1 ( s ) = 2 k w0 a 1( s ) = w(s ) s 2 + 2 xw0 s + w 2 0 (12) H k= k n - коефіцієнт пропорційності між a c і w де w0 = x= kn I - власна частота kq 2 1k n - коефіцієнт затухання тоді для БГС W( s ) = де: x= 2 1 .114k w0 a 2 (s ) = w(s ) s 2 + 0 .249xw0 s + 0. 707w 2 0 w0 = 0. 5k q 2Ik n (13) k kn = 0.707 n I AI = 0.353k q Ik n Знамения власної частоти w необхідно вибирати набагато більшою максимального значення частоти зміни вимірювальної швидкості. Для отримання задовільної якості перехідних процесів коефіцієнт затухання x , звичайно вибирають 0,4-0,7. Рівняння (12) в стандартній формі записується в наступному виді: a (s) k1 = W1 ( s ) = 1 2 2 w(s ) T1 s + 2xT1s + 1 (14) де T - постійна часу. Перехідний процес відповідно рівнянню (14) має вид: xt é ù - 1 1 e T1 sin( lT1 + Q 1 )ú a1 ( t ) = kê1 ê l T ú 1 1 ê ú ë û (15) l1 = 2 1 - x1 xp Q1 = arctg l 1T1 s 1 = k 1e l1T1 x1 T1 , де: Перехідний процес відповідно (15) подано на фіг. 7, поз. 1. Отож для БГС маємо: 2k W 2 ( s) = 2 2 T2 s + 0.707xT2 s + 1 (16) x 2t é ù 1 a 2 ( t ) = k 2 ê1 e T2 sin(l 2 t + Q 2 )ú ê l T ú 2 2 ê ú ë û (17) Перехідний процес відповідно рівнянню (17) приведено на фіг. 7, поз. 2. Порівняльний аналіз цих процесів показує, що швидкодія процесу поз. 2 і вище швидкодії поз. 1, так як період коливання поз. 1 p p p l2 l1 Для доказу перевага заявленої БГС наведемо розрахункові приклади. Приклад 1. Нехай передаточна функція відповідно рівнянню (11) має вид: a ( s) 10 = W1 ( s) = 1 0 w( s ) 0.04s + 0. 2s + 1 Де T = 0 .8 x1 = 0.5 Корні характеристичного рівняння 0 .01s 2 + 0 .2 s + 1 s = - 2. 5 ± 4.325 / дорівнюють 1,2 Веществена частина 1,5 показує коефіцієнт затухання перехідного процесу, мніма 4,325 - частоту затухаючих коливань, відкіль частота власних коливань дорівнює w0 = 6.25 + 18.705 = 5 x= 2.5 =5 5 а параметр затухання Функція чутливості a10 = 10w , а перехідний процес відповідає рівнянню [ a1 ( t ) = 10 1 - 1.033e -2.5 t sin(4.841t ) = Q 1 і приведено на фіг. 8, поз. 1: де X1 = ] 1 - 0. 0625 4 .43Q1 = arctg1 .772 0. 8 s1 = 10e -1. 6 = 2 s2 = 10e -3.2 = 0.48 ln s1 s2 = 1 .428 p 3. 14 = = 0 .7 l 1 4 .43 Період коливання дорівнює Приклад 2. Передаточна функція БГС 20 W 2 ( s) = 2 0.01s + 0 .14s + 1 Де T = 0.1 , а x = 0. 7 2 Корені характеристичного рівняння 0 .1s + 0.14 s + 1 = 0 s = - 7 ± 7 .141 i Дорівнюють 1,2 Функція чутливості має вид a 2 = 20w , що свідчить про підвищення чутливості у 2 рази. Перехідний процес [ ] a 2 ( t ) = 20 1 - 0. 714e -7 t sin( 7.141t + Q) представлено на фіг. 8, поз.2 де l2 = 1 - 0 .49 = 7.141 0. 1 Q 2 = arctg1. 02 s1 = 20e -3. 078 = 0.996 s 2 = 20e -6.151 = 0.4 w0 = 49 + 50 = 10 x= 7 = 0 .7 10 p 3. 14 = = 0 .4 l2 7. 141 період коливань дорівнює . Порівняння отриманих перехідних процесів фіг. 8, поз. 1 і 2 доказують підвищення швидкодії в 1.5 разів і, крім того, зменшення перерегулювання. В 1-му випадку воно складає s1 = 18.8% , що перевищує допустиму норму s1 = 5 %5% , а в другому випадку s = 4 .98% , що відповідає допустимим нормам. Приведені розрахункові приклади свідчать про досягнення поставлених задач. Література 1. Разыграев А.П. Основы управления полетом космических аппаратов. М, «Машиностроение», 1991,с.45. 2. Павловський М.А. Теория гироскопов. Киев, "Вища школа", 1986, с. 65. 3. Одинцов А.А. Теория и расчет гироскопических приборов. Киев, "Вища школа" 1985, с. 62. 4. Назаров Б.И., Хлебников Г. А. Гиростабилизаторы ракет. М.,. "Воениздат" 1975, с. 32.